Maybe the most important subject of sacred geometry is the Golden Mean. The Golden Mean is a very special ratio and is expressed by the Greek letter Ф called Phi.

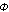= ½ * v5 + ½ = 1.618

Phi like Pi is an irrational number, meaning you can never calculate its exact value, you can only approximate it.

The Phi ratio is expressed in the Golden Section. The Golden Section is a the length of let’s say a rope when it is divided such that the ratio of the longer part of the rope to the whole is exactly the same ratio as the shorter part of the rope is to the longer part. (Read it again)

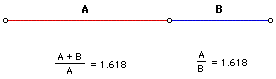
When the Phi ratio is applied to a rectangle whereas B = 1 and A has length Ø, the rectangle is called a Golden Rectangle.

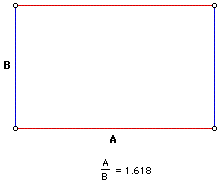
The Golden Rectangle can be used to create a spiral, the Golden Spiral. Starting with one Golden Rectangle, a second Golden Rectangle can be attached to the first using the longest side of the rectangle, side A as the shortest side B of the next rectangle. To this end the second rectangle is constructed 90 degrees perpendicular to the first rectangle. If this process is continued, called the spiralling of the Golden Rectangle, a curved line can be drawn through the corners of the rectangles creating the Golden Mean spiral. The spiralling of the Golden Mean spiral continues indefinitely in inward and outward directions, it’s getting smaller and smaller spiralling inwards and getting bigger and bigger spiralling outwards.

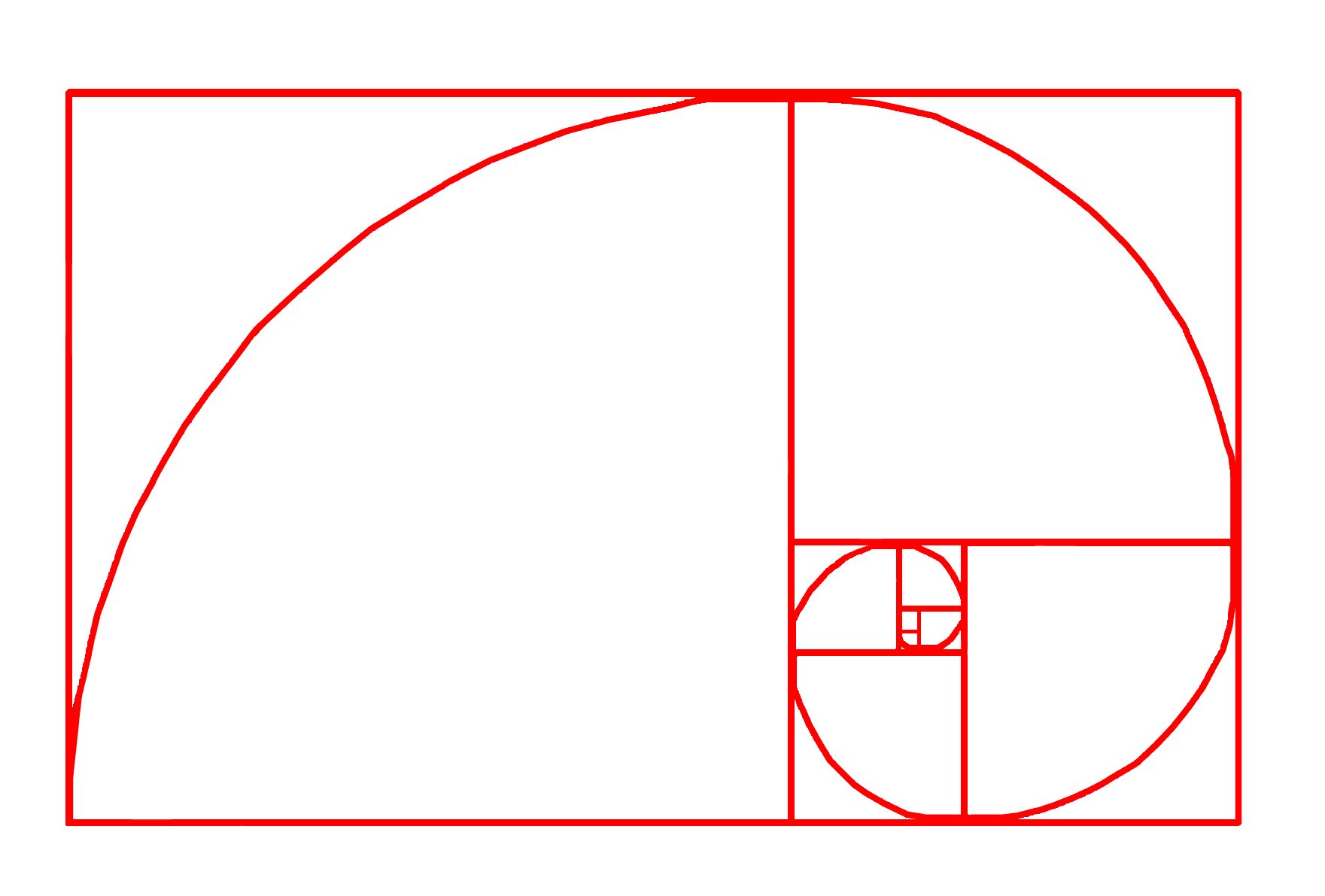
Golden Mean spiral

A variant of the Golden Mean spiral is the Fibonacci spiral. The difference with the Golden Mean spiral is that is does not spiral in indefinitely but starts with a Golden Rectangle of which one side has length 1 and the other length Phi.
Gradually when the Fibonacci spiral, spirals outward, there will be no distinction noticeable any more between a true Golden Mean spiral and the Fibonacci spiral. The Fibonacci spiral is based on the progression of the Fibonacci sequence.

Crop circle, fractal spirals, Milk Hill, Wiltshire august 12th 2001

Fibonnaci sequence

Leonardo Fibonacci (1175 AD), a great mathematician of the Middle Ages discovered the Fibonacci sequence by studying nature. He studied the growth of rabbit populations and the growth of leaves and petals and discovered a well-defined mathematical sequence in all of this.

This is the Fibonacci sequence:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 etc.

Each number in the sequence is the sum of the two preceding numbers starting with the root number 1. The Fibonacci sequence progresses towards the Golden Mean if we divide two successive numbers in the sequence.

1/1       = 1
2/1       = 2.0
3/2       = 1.5
5/3         = 1.667
8/5         = 1.60
.
144/89 = 1.618

The Fibonacci sequence propagates towards Phi (Ø) but never reaches it since it is an irrational or transcendent number.

Fibonacci spirals and Golden Mean ratios appear everywhere in the universe. The spiral is the natural flow form of water when it is going down the drain. It is also the natural flow form of air in tornados and hurricanes. Here’s another beautiful example of a Fibonacci spiral in nature, it’s the Nautilus shell and every book about sacred geometry contains one:

Nautilus shell

The Golden Mean ratio is all over the human body, in the ratios between the bones, the length of your arms and legs. The Golden Mean is also the ratio in the distance from the navel to your toe and the distance from your navel to the top of your head. Michelangelo has beautifully hidden these Golden Mean ratios in his fresco on the ceiling of the Sistine Chapel in Rome:

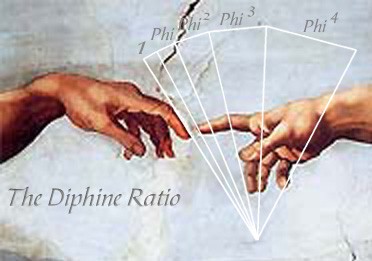
Michelangelo and the Phi ratios in the human hand
(Courtesy of Frank van den Bovenkamp, www.frankvandenbovenkamp.com)

A classical mathematical problem dating all the way back to Plato is called ‘squaring the circle’. In the last three thousand years mathematicians have tried to come up with a solution using only a pair of compasses and straightedge on how the construct a circle and square such that they have the same perimeter. In 1882 Lindemann proved that there is no solution to this problem. Since Lindemann’s proof is rather complex, we will show in simple terms why the circle cannot be squared. The circumference of the circle with a radius of one is 2 * π and π (Pi) is an irrational number (a transcendent number, π can never be measured only be approximated!). But when Pi is irrational and cannot be measured so is the circumference of the circle! However the square’s circumference is a real number since it equals 4 times the side of the square that is a real number that can be measured. Hence the circumference of both circle and square will never be equal in the mathematical sense; however they can become infinitely close.

Vitruvian man

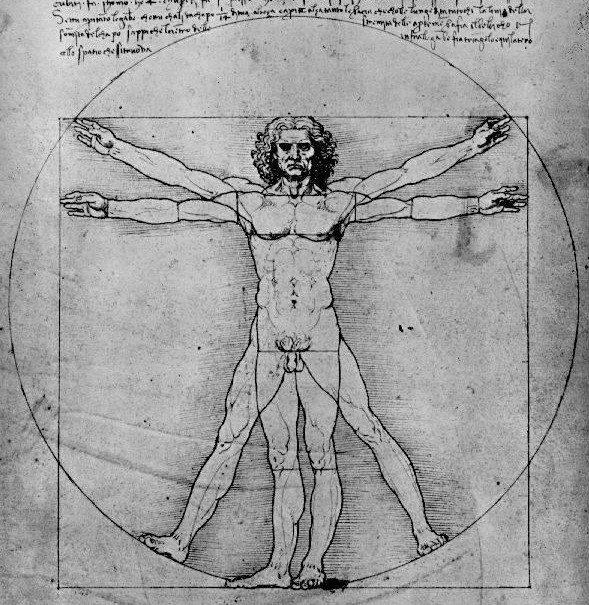
Now here’s an interesting drawing from Leonardo Da Vinci. What he is showing in this sketch is that the human body ‘squares the circle’. When man stretches his arms and holds them horizontally, man’s body will perfectly fit into the square. On the other hand, when he spreads his legs and raises his arms as in the sketch, man’s body can be perfectly circumscribed by a circle. The circumference of the square ‘equals’ that of the circle.

A lot has been written about this sketch alone, it contains a whole lot of hidden sacred geometry. We will not go into all the details here, but I want to show you some very amazing things. Ancient wisdom, the Hermetic tradition tells us that the human body can be regarded as a blueprint for the universe by means of all the ratios that are found within the body. This may indeed be true. Let’s have a look at the following picture:

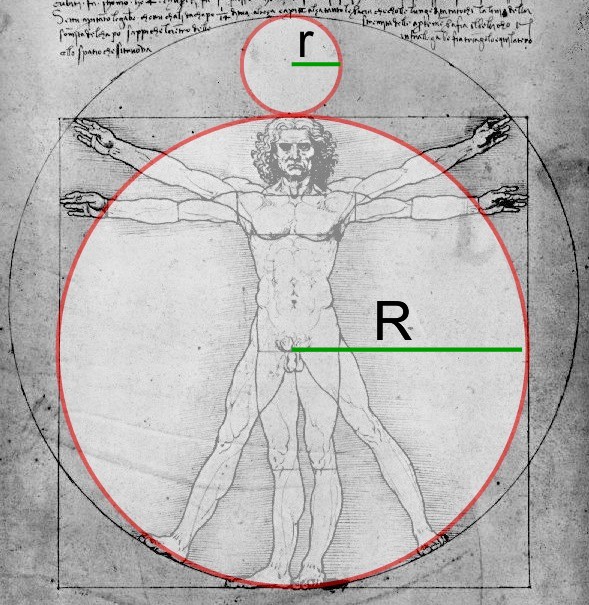
This is the same picture as above, in the picture there are now two red circles added. The biggest red circle fits perfectly and is inscribed by the square. The smaller red circle’s is centered between the outer circle and the inner red circle and tangentially touches both.

Much to our surprise, the upper red circle represents the moon and the lower red circle represents the Earth!  In mathematical terms: The ratio of the diameter of the smaller red circle to the bigger red circle r / R equals the ratio of the diameter of the moon to the diameter of the Earth! Now let’s prove it:
(3)

Radius of the moon : r
Radius of the Earth : R
Side of the square is : 2R
The perimeter of the square is : 8 R
Radius of the outer circle is : r + R
The circumference of the outer circle is : 2 p ( r + R )

Now ‘squaring the circle’ makes the perimeter of the square equal to the circle:

8 R = 2 p ( r + R )

8 R - 2 p R = 2 p r

R (8 – 2 p) = 2 p r

r / R = (8 – 2 p) / 2 p = (4 – p) / p

Earth radius = 6,370,973 m
Moon radius = 1,738,000 m
Moon to Earth ratio = r / R = 0.27279977
r / R = (4 – p) / p = 0.273239544 (p = 3.14159265)

Quod Erat Demonstrandum!

There is another mysterious relation to be discovered in the sketch of the Vitruvian man by Leonardo Da Vinci. The Great Pyramid at the Giza plateau in Egypt called after the pharaoh that is supposedly buried there named Khufu (Cheops in Greek), holds a perfect geometrical relation to the squaring of the circle and the Vitruvian man as depicted by Leonardo Da Vinci!

Look at the picture below:

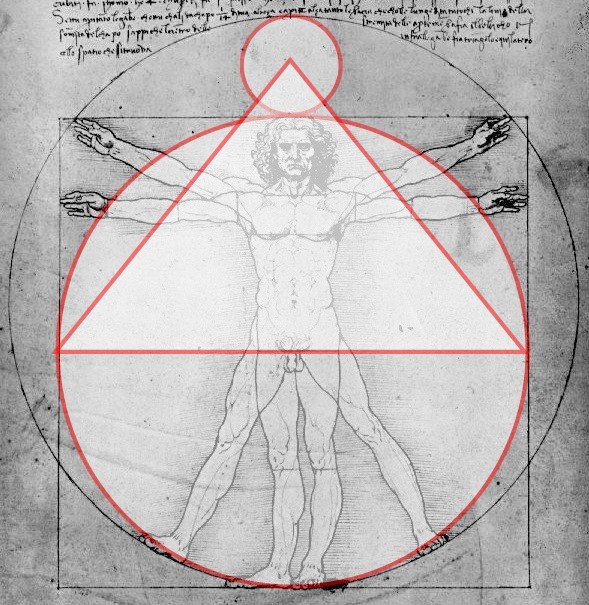
Great Piramid at Giza in relation to Vitruvius man

The triangle in the picture is the exact geometrical proportion of the Great Pyramid at the Giza Plateau near Cairo, Egypt. The angles between the base and the apex (top) of the pyramid are exactly 51 degrees and 51 seconds. (51º 51’). 
(4)

The Great Pyramid and in fact the complete layout of the Giza plateau with all its pyramids, sacred temples and the sphinx contains a lot of hidden sacred geometry of which we will reveal more in this book. The point I want to make here is that the Egyptians were aware of the art of sacred geometry and how it relates to the universe, as the Giza plateau and in particular the Great Pyramid proves.

Let there be light

While explaining the Genesis pattern of sacred geometry we mentioned that on the second day of creation God created the Vesica Pisces and that the Vesica Pisces is the geometry of the light particle the photon. The Holy Bible mentions the second day of creation as the creation of the light. By the way did you notice that the Vesica Pisces has the shape of the eye?

It was discovered by Buckminster Fuller, who did a lot of the groundwork in re-establishing sacred geometry, that the geometry of the photon must be two tetrahedrons joined at a common face.

Now the geometrical shape of the double tetrahedron is perfectly circumscribed by the Vesica Pisces whereas the vertices of the tetrahedrons neatly touch the face of the Vesica Pisces. This has been confirmed by Drunvalo Melchizedek another sacred geometry architect!
(5)
 
The tetrahedron is also the hidden geometry in the electromagnetic wave (wave form of light) itself. The electrical and magnetic fields are perpendicular to each other and a spiral can be drawn connecting the electrical field with the magnetic field that exactly traces over a tetrahedron!

Tom Bearden, the inventor of the MEG machine has proof that James Clerk Maxwell must have known this but that Oliver Heaviside removed the knowledge of the hidden tetrahedron in the simplified version of electrodynamics.
(6)

Notre-Dame de Chartres

The knowledge of sacred geometry has been preserved in the architecture of churches and cathedrals all over Europe. The cathedral of Chartres is famous for its sacred geometry that was used in its design. Sacred geometry can be found for example in the layout of the ground plan and the stained glass windows that contain the Phi ratio.
                    

In the Gothic nave of the cathedral we find an enigmatic labyrinth on the floor made out of white stone and set within dark marble. The labyrinth measures almost exactly one tenth of the interior length of the cathedral and it is used as the central point, the focus of the whole geometric construction of the cathedral. Obviously the designers thought it to be very important

The diameter of the labyrinth measures exactly the size of the west rose window shown in the picture above. At the same time the distance from the center of the west rose window to the floor is the same distance as the distance from the center of the labyrinth to the west portal wall of the cathedral. In other words the west rose window and the labyrinth form a perfect equilateral triangle.

Labyrinth on ground floor of the nave

I personally visited the Chartres Cathedral a few times. During my last visit, in the summer of 2004, I noticed a young couple, a boy and a girl. The girl kneeled down at the center of the labyrinth and went into a meditation, hands held high into the air. The boy sat beside her. The couple were totally undisturbed by the crowd that passed by although they drew a lot of attention! I was intrigued. Obviously the couple knew something more about the sacredness of the labyrinth and they had chosen this spot for their meditation. But what could it possibly mean?

If we meander through the labyrinth we have to make these alternating left and right turns. At the same time we turn inwards and outwards until we enter the center. According to Daniel Winter, whose physics we will study in the next chapter, the labyrinth is the two dimensional symbolic projection of the Phi spirals that make up a torus. The torus is assumed in his aether physics to be the building block of matter and the atom. The labyrinth according to Winter is a symbolic projection of the twists and turns the Phi spirals of light take while centring into the nucleus of the atom.

The Chartres cathedral secretly contains knowledge of sacred geometry; however it took many ages before it was discovered. Sacred geometry was used in many more cathedrals and churches throughout France such as the ones of Rheims, Sens, Arras, Amiens, St Quentin, Bayeux and Toulouse to name a few. All of them contained labyrinths quiet similar to the one in Chartres. The labyrinth obviously was very important.
 
France was the home of the Merovingian Kings a bloodline that were believed to be the descendants of Jesus Christ. Many authors now claim that Jesus had children with Mary Magdalene and that the Catholic Church kept this fact secret for many ages. The idea has gained a lot of public awareness since the book the ‘Da Vinci Code’ by Dan Brown was released in the summer of 2004. The descendants of Jesus are the bloodline of the Holy Grail. Traces of this bloodline lead to Rennes Les Chateaux in France and Roswell Chapel in Britain, the homeland of the Knights Templar and King Arthur. This secret of Jesus’s his marriage to Mary Magdalene and of his offspring was carefully preserved in secret societies.

It is now believed that these secret societies also preserved scientific and Gnostic knowledge that can be traced back to the mythological Atlantis. The Atlantean knowledge was supposedly passed on to the Egyptians and from the Egyptians to the Greek Hermetic tradition. In modern times it was preserved in secret circles of Freemasonry that have existed throughout the ages. Leonardo Da Vinci was a member of such a circle that gave him access to the science of sacred geometry and his membership explains why he used it in his paintings. The importance of sacred geometry especially the meaning of the Golden Mean has been used in many art forms in modern history, from the paintings of Leonardo Da Vinci to the architecture of churches and cathedrals and in music such as Beethoven’s Fifth symphony.

(7)

Recapitulation

This chapter was a lecture in sacred geometry. I would not have introduced it in this book if it didn’t play such a significant role in a new physics that is unfolding. Science is discovering the geometrical and fractal patterns described by sacred geometry in our physical universe, the gravitational and electromagnetic energy fields of the Earth, the structure of the atom and the energy fields of the human body.

In chapter 3 we showed that the separation once suggested by René Descartes that there is a strict segregation between the physical and the mental dimensions is false. The human mind is very powerful and has powers of mind over matter. Quantum physicist Amit Goswami suggested that consciousness is primordial and that the physical realm is created from it.

In chapter 4 we discussed the zero point field that was discovered by quantum science. The zero point field is an unlimited inexhaustible energy field that is present everywhere in the universe. We suggested that the zero point energy might be the spiritual energy required to sustain Amit Goswami’s claim.

In this chapter we studied sacred geometry an ancient science that is being rediscovered by contemporary scientists.

In the next chapter we will use sacred geometry, the zero point field and our understanding of consciousness and show how scientists today assimilate it into a new model of physics, a theory of everything that explains both the physical and the mental domain. We will also see that contemporary science is rediscovering what Plato 2350 years ago suggested: that the world of the atom is constructed from the Platonic solids and discover the importance of the Golden Mean in waveforms.