Números poligonales
Fecha de primera versión: Marzo 1997
Fecha de última actualización: 26-06-01

Los números poligonales se remontan al comienzo mismo de la matemática. Fueron los pitagóricos los que los descubrieron.
Tal vez, la mejor forma de comprender los números poligonales es percatarse que en aquella época los números se representaban mediante guijarros (calculi) que se disponían en una superficie.
Algunos números pueden disponerse formando figuras geométricas, por ejemplo 3 guijarros se pueden disponer formando un triángulo, 4 forman un cuadrado, etc.
Los números triangulares (1, 3, 6, 10, 15, ...) son enteros del tipo N = 1 + 2 + 3 + ... + n
Los números cuadrados (1, 4, 9, 16, 25, ...) son enteros del tipo N = 1 + 3 + 5 + 7 + ... + (2n-1)
Los números pentagonales (1, 5, 12, 22, ...) son enteros del tipo N = 1 + 4 + 7 + ... +(3n-2)
Los números hexagonales (1, 6, 15, 28, ...) son enteros del tipo N = 1 + 5 + 9 + ... + (4n-3)
Y así sucesivamente.
En general, los números poligonales son enteros del tipo 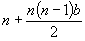 .
.
Cuando b=1 se dice que es un número triangular, para b=2 cuadrados, para b=3 pentagonales.
Los números poligonales se pueden obtener mediante recurrencia (sea n el número de orden del número poligonal):
T(n) = T(n - 1) + n
C(n) = C(n - 1) + (2n - 1)
P(n) = P(n - 1) + (3n - 2)
...................................
M(n) = M(n -1) + (m - 2)(n - 1) + 1
Observemos que si tomamos el primer número de cada serie de números poligonales (3, 4, 5, 6, ...) obtenemos una progresión aritmética de diferencia 1. Si tomamos el segundo número de cada serie (6, 9, 12, 15, ...) obtenemos una progresión aritmética de diferencia 3, y así sucesivamente
Según Fermat, todo número entero puede expresarse mediante la suma de n números n-gonales como máximo. Gauss demostró esta conjetura para los números triangulares y cuadrados, Cauchy consiguió dar una demostración general.
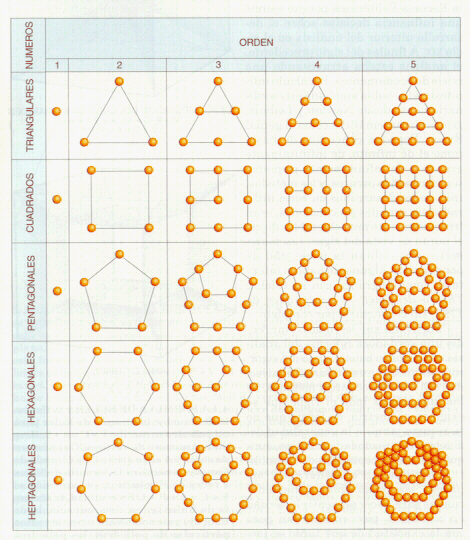
De la observación de la figura se deduce que todo numero cuadrado (de cualquier orden) es la suma de un número triangular del mismo orden y otro de orden inmediatamente anterior. Por ejemplo: 9 = 6 + 3, 25 = 15 + 10. Esto se puede representar de esta forma: C(n) = T(n) + T(n - 1).
Un número pentagonal se puede obtener como la suma de uno triangular del mismo orden más dos veces otro de orden inmediatamente anterior. Por ejemplo: 22 = 10 + 2.6. Eso se puede representar de esta forma: P(n) = T(n) + 2T(n - 1).
Un número hexagonal se puede obtener como la suma de uno triangular del mismo orden más tres veces otro de orden inmediatamente anterior. Por ejemplo: 28 = 10 + 3.6. Eso se puede representar de esta forma: H(n) = T(n) + 3T(n - 1).
La fórmula general para un número poligonal de m lados sería: M(n) = T(n) + (m - 3).T(n - 1).
C(n) = T(n) + T(n - 1).
P(n) = C(n) + T(n - 1).
H(n) = P(n) + T(n - 1).
...............................
Algunos números pertenecen a dos familias diferentes. Por ejemplo: 36 es un número triangular de orden 8 y cuadrangular de orden 6.

