GRAN PIRAMIDE DISEÑADA EN FUNCION A LA MANZANA DORADA (NUMERO DE ORO PHI=1.618033), AL NUMERO 4 (CUATRO FASES DE LA LUNA CADA SIETE DIAS O CUARTO MANDAMIENTO CON REFERENCIA AL SEPTIMO DIA) QUE TAMBIEN ES EL CUADRADO DE LA CUADRATURA, AL CIRCULO (POLIGONO DE INFINITO=NUMERO 8=OCTAVO DIA) QUE ES LA CONVERSION DEL AGUA EN VINO, EN EL MARCO A LAS BODAS DE CANA.
Squaring the Circle - The Great Pyramid
|
The square represents the physical. The circle represents the spiritual. All sacred geometers have attempted the impossible: to square the circle (create a square who's perimeter is equal to the circumference of a circle.)
Here is the first of two valiant attempts:
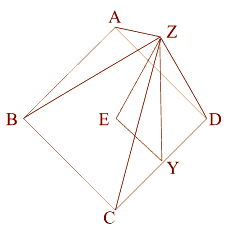
This squaring of the circle works with a right triangle that represents the apothem (ZY) - (a line drawn from the base of the center of one of the sides to top of the pyramid), down to the center of the base (ZE), and out to the point where the apothem touches the Earth (EY).
|

The Great Pyramid of Egypt
(Sphinx in foreground)
|
|
|
Now let's look at this in 2D,
from directly above.
For the purpose of this exercise,
the side (AB) of the base equals 2.
|
|
|
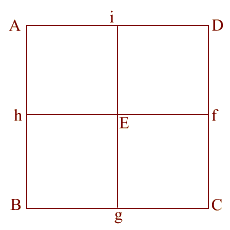
(ABCD) is the base of the Great Pyramid.
This is lettered similarly to the wire frame version (above).
For the purpose of this exercise,
the side (AB) of the base equals 2.
|
|
|
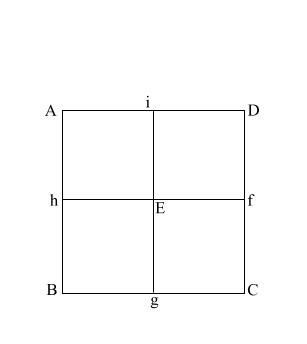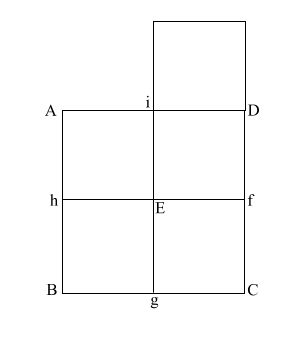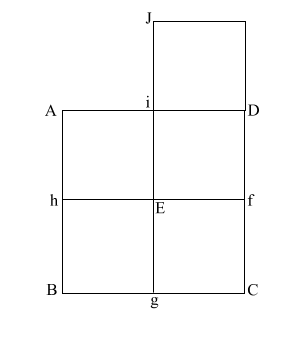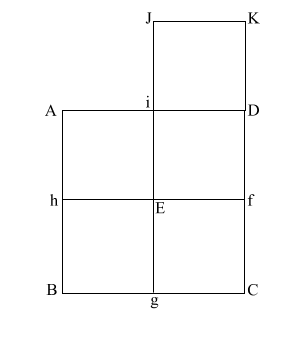
Construct square (i JKD),
thus creating double square (JKE f).
|
|
|
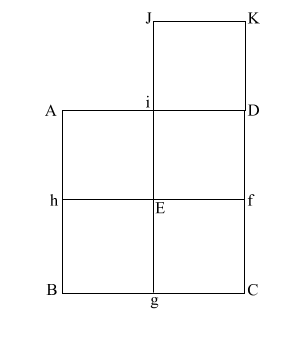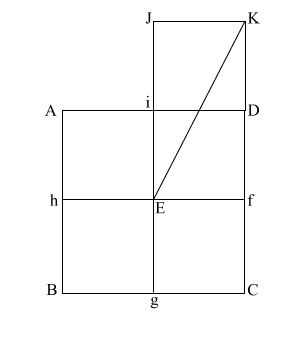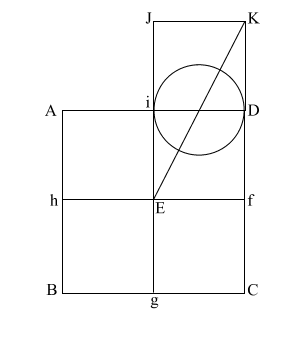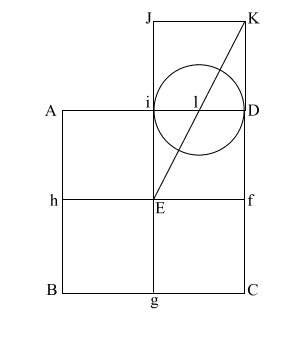
Create diagonal (EK)
which intersects (i D) at (l).
iD = 1,
therefore the diameter
of the circle is also 1.
(EK) = ( 5) = .618 + 1 + .618 5) = .618 + 1 + .618
|
|
|
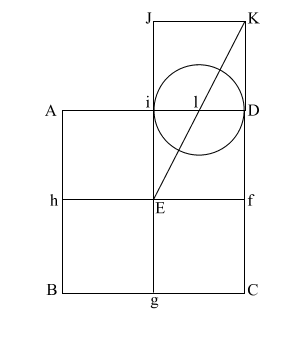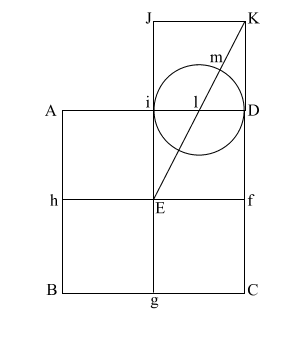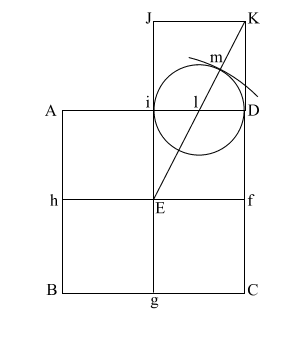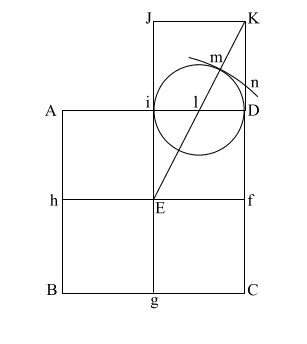
Put the point of your compass at (E) and extend it along the diagonal (EK) to point (m) where the circle intersects (EK), and draw the arc downward to intersect (KD f C) at (n).
If (EK) = ( 5), and (l m/l D) and l i = .5, the diameter of this circle is 1. 5), and (l m/l D) and l i = .5, the diameter of this circle is 1.
This makes (E m) = .618 + 1, or 1.618.
(E m) is the apothem.
|
|
|
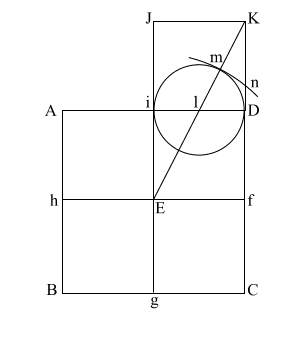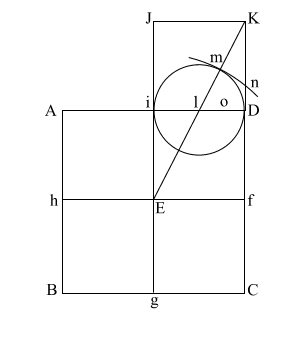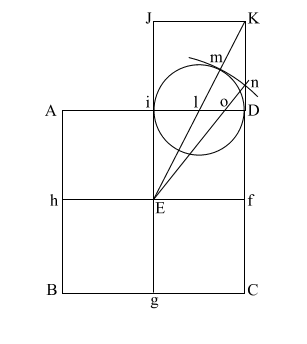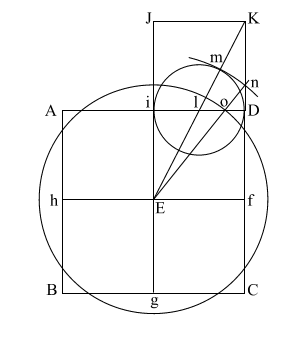
Draw (E n) which intersects (A i l D ) at (o).
Put compass point at (f) and extend it to (n). Again put your point at (E) and draw the circle which happens to have the radius (E o).
(f n) is the height of the Great Pyramid.
This circle comes remarkably close to having the same circumference as the perimeter of the base (ABCD).
|
|
Let's go back to the original right triangle (EYZ)
(EY) = .5
(YZ) = phi
(EZ) = ( phi) phi)
EY = .5, The apothem is phi/1.618. This makes the 51 degree + degree angle.
Using a² + b² = c², this makes the height the square root of phi.
|
Squaring the Circle - The Earth & the Moon
|
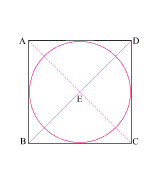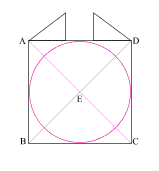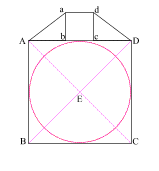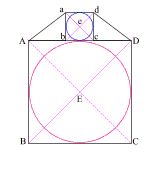
Create a square (ABCD) with (AB) = 11
Create diagonals (AC) and (BD) crossing at center point (E)
Construct a circle which is tangent to square (ABCD) at f
|

|
|
Construct two 3 . 4 . 5 right triangles, with the 4 . 5 angles at (A) and (D).
Connect the 5 . 3 angles creating square (abcd) with side (ab) = 3
{4 + 3 + 4 = 11, or side (AD) of square (ABCD)}
Create diagonals (ac) and (bd) centering at (e)
Create a circle that is tangent to square (abcd) at four places.
|
|
|
Draw line (Ee) which intersects side (AD) at (F)
(EF) = the radius of the larger circle and (eF) = the radius of the smaller circle
The larger circle thus created is to the smaller circle as the moon is to the Earth!
With your compass point at (E), create a circle with radius (Ee)
This creates a circle whose circumference is equal to the perimeter of square (ABCD)!
|

|
The Math:
|
1
(AB) = 11
(EF) = 1/2 of (AB) = 5.5
(ab) = 3
(eF) = 1.5
Therefore 5.5 + 1.5 = 7
The circumference of a circle is equal to two times the radius (the diameter) times pi (3.1416).
C= 14 x 3.1416
C= 43.9824
|
2
In Square (ABCD), (AB) = 11
The perimeter of a square is four times one side. 11 x 4 = 44
According to the Cambridge Encyclopedia, the equator radius of the Earth is 3963 miles. The equator radius of the Moon is 1080.
The claim is that the smaller circle (in square abcd) is to the larger circle (in square ABCD) as the Moon is to the Earth.
|
|
3
(EF) = 5.5
(F e) = 1.5
5.5 : 1.5 :: 3963 : 1080
5.5 / 1.5 = 3.66666
3963 / 1080 = 3.6694 - (if it had been 3960, it would have been exact!)
|
EL NUMERO DE ORO PHI=1.618033 SALE MATEMATICAMENTE DE LA UNION DE DOS CUADRADOS (FORMA DE NUMERO OCHO)
|

