Srinivāsa Aiyangār Rāmānujan, en tamil : ஸ்ரீனிவாஸ ஐயங்கார் ராமானுஜன், (Erode 22 de diciembre de 1887 - Kumbakonam 26 de abril de 1920) fue un matemático indio. De familia humilde, a los siete años asistió a una escuela pública gracias a una beca. Recitaba a sus compañeros de clase fórmulas matemáticas y cifras de π.
A los 12 años dominaba la trigonometría, y a los 15 le prestaron un libro con 6.000 teoremas conocidos, sin demostraciones. Ésa fue su formación matemática básica. En 1903 y 1907 no aprobó los exámenes universitarios porque sólo se dedicaba a sus diversiones matemáticas.
En 1912 fue animado a comunicar sus resultados a tres distinguidos matemáticos. Dos de ellos no le respondieron, pero sí lo hizo Godfrey Harold Hardy, de Cambridge. Hardy estuvo a punto de tirar la carta, pero la misma noche que la recibió se sentó con su amigo John Edensor Littlewood a descifrar la lista de 120 fórmulas y teoremas de Ramanujan. Horas más tarde creían estar ante la obra de un genio. Hardy tenía su propia escala de valoración para el genio matemático: 100 para Ramanujan, 80 para David Hilbert, 30 para Littlewood y 25 para sí mismo. Algunas de las fórmulas de Ramanujan le desbordaron, pero escribió ...forzoso es que fueran verdaderas, porque de no serlo, nadie habría tenido la imaginación necesaria para inventarlas. Invitado por Hardy, Ramanujan partió para Inglaterra en 1914 y comenzaron a trabajar juntos. En 1917 Ramanujan fue admitido en la Royal Society de Londres y en el Trinity College, siendo el primer indio que lograba tal honor. De salud muy débil, murió tres años después.
Hardy escribió de Rāmānujan:
"Los límites de sus conocimientos eran sorprendentes como su profundidad. Era un hombre capaz de resolver ecuaciones modulares y teoremas ...de un modo jamás visto antes, su dominio de las fracciones continuas era...superior a la de todo otro matemático del mundo; ha encontrado por sí solo la ecuación funcional de la función zeta y los términos más importantes de la teoría analítica de los números; sin embargo no había oído hablar jamás de una función doblemente periódica o del Teorema de Cauchy y poseía una vaga idea de lo que era una función de variable compleja..."
Lo principal de los trabajos de Ramanujan está en sus cuadernos, escritos por él en nomenclatura y notación particular, con ausencia de demostraciones, lo que ha provocado una difícil tarea de desciframiento y reconstrucción, aún no concluida. Fascinado por el número π, desarrolló potentes algoritmos para calcularlo.
Rāmānujan trabajó principalmente en la teoría analítica de los números y devino célebre por sus numerosas fórmulas sumatorias referidas a las constantes tales como π y la base natural de los logaritmos, los números primos y la función de fracción de un entero obtenida junto a Godfrey Harold Hardy.
Rāmānujan nació en la localidad de Erode, del estado de Tamil Nadu en India, en el seno de una familia brahman pobre y ortodoxa. Fue un llamativo autodidacta; prácticamente todas las matemáticas que aprendió fueron las leídas hacia los 15 años de edad en los libros La Trigonometría plana de S. Looney, y la Synopsis of Elementary Results in Pure Mathematics de S. Carr que contenían un listado de unos 6000 teoremas sin demostración. Estas dos obras le permitieron establecer una gran cantidad de conclusiones y resultados atinentes a la teoría de los números, las funciones elípticas, las fracciones continuas y las series infinitas para esto creó su propio sistema de representación simbólica.
A la edad de 17 años llevó a cabo por su cuenta una investigación de los números de Bernoulli y de la Constante de Euler-Mascheroni. Se licenció en el Government College de Kumbakonam.
El matemático seguía una estricta vida de Brahmin. A menudo decía que sus teoremas matemáticos eran inspirados directamente por la diosa Namagiri, durante sus sueños. Algunos de sus numerosos teoremas, han resultado ser en realidad incorrectos. Se desconocen los métodos mentales empleados por la mente de Rāmānujan para desarrollar sus intuiciones matemáticas, la mayoría de las veces completamente ciertas, pero en algunos casos falsas.
Rāmānujan, de un modo independiente, recopiló 3900 resultados (en su mayoría identidades y ecuaciones) durante su breve vida.
Afectado por una tuberculosis que se agravaba por el clima de Inglaterra, Rāmānujan retornó a su país natal en 1919 y falleció poco tiempo después en Kumbakonam (a 260 km de Chennai Madras) a la edad de 32 años. Dejó varios libros llamados Cuadernos de Ramanujan los cuales continúan siendo objeto de estudios.
Recientemente, las fórmulas de Rāmānujan han sido fundamentales para nuevos estudios en cristalografía y en teoría de cuerdas. El Ramanujan Journal es una publicación internacional que publica trabajos de áreas de las matemáticas influidas por este investigador indio.
Teoremas y descubrimientos[editar]
Aquí se reportan algunos de los hallazgos de Ramanujan, y los resultados obtenidos en colaboración con Hardy a inicios del siglo XX:
Ha logrado notables progresos y descubrimientos en las áreas relativas a :
La conjetura de Rāmānujan y su importancia[editar]
Aunque existen numerosas expresiones que reciben el nombre de "conjetura de Ramanujan", existe una particularmente influyente sobre los trabajos sucesivos. Esta conjetura de Ramanujan es una aserción referente a las dimensiones de los coeficientes de la función Tau, una típica forma cúspide en la teoría de las formas modulares. Y ha sido finalmente demostrada posteriormente como consecuencia de la demostración de la conjetura de Weil mediante un complicado procedimiento.
Entre muchas otras, Rāmānujan ha aportado la siguiente fórmula:
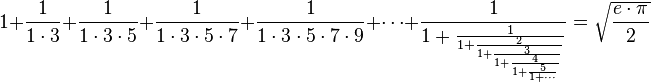
Se trata de una especie de obra de arte matemática donde se conecta una serie matemática infinita y una fracción continua para aportar así una relación entre dos célebres constantes de matemáticas.
Una segunda fórmula, demostrada en 1985 por Jonathan y Peter Borwein, es la que descubrió él en 1910 :
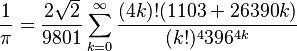
Es muy eficaz porque ella aporta 8 decimales a cada iteración.
Número de Ramanujan[editar]
Se denomina número de Hardy-Ramanujan a todo entero natural que se puede expresar como la suma de dos cubos de dos maneras diferentes. Hardy comenta la siguiente anécdota :
Recuerdo que fui a verle una vez, cuando él ya estaba muy enfermo, en Putney. Había tomado yo un taxi que llevaba el número 1729 y señalé que tal número me parecía poco interesante, y yo esperaba que él no hiciera sino un signo desdeñoso.
- "No"- me respondió- este es un número muy interesante; es el número más pequeño que podemos descomponer de dos maneras diferentes como suma de dos cubos.
En efecto, 
.
- Otros números que poseen esta propiedad habían sido descubiertos por el matemático francés Bernard Frénicle de Bessy (1602-1675) :
- El más pequeño de los números descomponibles de dos maneras diferentes en suma de dos potencias a la cuarta es 635 318 657, y fue descubierto por Euler (1707-1763):
Se denomina nésimo número Taxicab, denotado como Ta(n) o Taxicab(n), al más pequeño número que puede ser expresado como una suma de dos cubos positivos no nulos de n maneras distintas, sin contar variaciones del orden de los operandos. Así, Ta(1) = 2 =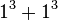 
, Ta(2) = 1729 y Ta(3) = 87539319. Variante del taxicab es el cabtaxi (un número cabtaxi es definido como el número entero más pequeño que se puede escribir de n maneras diferentes (en el orden de los términos aproximados) como suma de dos cubos positivos, nulos o negativos).
Véase también[editar]
Thème précédent
