|
|
| Daniel, the Magi and the Luni-solar Calendar of Israel
An interesting aspect of the teachings of the Magi comes from their founder, Zoroaster whose writings in the Zend Avesta, uphold much of the depth of meaning we found in Numbers 24:17. The Magi may have also applied this prophecy to the return of the older Zoroaster. The ancient roots of the Zoroastrianism lie in the ancient Persian traditions, and share many common elements with Judaism and Christianity. The tenets of the Christian Faith were preserved by God and handed down to other faithful men via the oral traditions, even as the truths of the Biblical Patriarchs were. The historical record bears this out, relating to the important point of how the Babylonian zodiac of 12 signs each of 30 degrees was transmitted to ancient Greece. Many scholars are not certain, as to the process by which this occurred, thus its an engaging point of history that both the ancient Greeks and Babylonians came under the rule of the Persian empire initiated by Cyrus the Great in 539 BC. It was during the rule of Darius I "the Mede" that the Prophet Daniel presided over his Court Astronomers and Chaldeans. Drawing on the rich astronomical traditions of the Biblical Patriarchs not to mention, the famous astronomical expertise of the Persian Magi, Daniel's potent influence convinced Darius to adopt some salient principles of Biblical Astronomy in the period around 522 BC. Certain important aspects of Zoroastrianism agreed with the Biblical standard practiced by the Hebrews, carried on by Daniel. The Magi would certainly have been familiar with Daniel's prophecy concerning the 70 weeks judged on Jerusalem relating to the coming Messiah, [Dan. 9:2, 24-27]. Daniel's influence had the added effect of preserving the astronomical truths of the promised seed, contained in the form of the zodiacal narrative, which God put in the most capable hands of the time. To illustrate this point more robustly, let's look at the practice of the Intercalation of months in the Hebrew Lunar Calendar, an important part of this practice of the Israelites in preserving their astronomical heritage.
We know the Hebrew practice of Intercalation of months dates back at least to the time of Moses, who instituted the sacred observances of the Old Testament Law during Israel's wanderings in the wilderness in the mid-second millennium BC. This preceded Meton of Athens who is given credit for discovering the saros in 432 BC, by at least a thousand years. The roots of the word "saros," and its practices however are much older. The Calendar of Israel is governed by the 354-355 day lunar year with twelve months of 29 or 30 days. The named months of the Israelite year coincide with the Babylonian months, including Adar Sheni, the extra 13th month which was added to keep the solar year aligned with the seasons. The practice of Intercalation of months kept the holidays of Passover, Pentecost and Rosh Hashanah, just prior to the Feast of Tabernacles in the month of Tishri, in their proper seasons of early Spring, the beginning of summer and at summer's end. The "11-day gap between the solar & lunar years expands to a period of seven months over this 19-year lunar cycle. In the Calendar of Israel a total of seven years (3rd 6th, 8th, 11th, 14th, 17th and 19th) during this 19-year lunar cycle, would normally contain an extra month of Adar Sheni."1
With every 19 solar years plus two hours, the Sun and Moon return to meet each other at the same appointed time and place in the sky. The saros, however, consists of 19 eclipse years, which is only 18 solar years plus eleven days. An eclipse year thus consists of 346.62 solar days, which is equal to 11.738 lunations. When we divide the saros by 11.738, we get 1.618, (or phi),2 accurate to 4 digits! Since the Sun intersects a lunar Node two times every 346.62-day eclipse year, we find the cycle of the celestial rendezvous of the Sun and Moon also governed by the phi ratio. The Hebrew calendar also unifies these luni-solar cycles according to phi, in concert with Israel's sacred fifty-year cycle of Jubilees. This is evident because there are 618 lunations in any given 50-year Jubilee cycle. Thus, as the Hebrew calendar shows the perfect correlation of the sacred and secular celestial cycles, governing the rhythms of a myriad terrestrial and cosmic cycles, we find more evidence of the signature of God the Creator and His rulership of light reflected in the heavens, the Source behind all kingdoms of earthly life. This exhibits the perfect relation between the civil [lunar], and sacred [solar] years of the Calendar of Israel, in the larger context of precession. These related standards of the sacred and secular are also unified in the promised seed, Jesus Christ as the Priest--King of Israel, and light of the world presiding over all circadian rhythms and other aspects of the kingdoms of terrestrial life.
As we briefly mentioned earlier, the roots of the word for saros are much older than Meton's application of the term. In fact it goes back at least as far as ancient Sumeria, because the Sumerian name for the great lunar eclipse cycle was also called the saros. This word traces through to the basic Babylonian unit of measure, also called a "sar," showing ancient elements of the sacred celestial rule of measure. This period of lunation consisting of 18 years & 11, (10.96) days, was utilized by the Chadean priests to predict eclipses. Wallis Budge supported this notion when he stated; "the Babylonians were a nation of stargazers observing the appearances of the moon, eclipses, & planets etc." This was the culture that produced the Magi, and speaks volumes on not only their astronomical expertise, but also their focus while watching the heavens for the celestial signs revealing the birth of the promised seed. The Chaldeans also had a period of 3600 (60 x 60) years that they called a saros. Here again we see the Sexegesimal pattern behind the organization of the heavens, including the cycle of the Moon joining Saturn and Jupiter every 60 years in their celestial dance. Jupiter-Saturn Conjunctions exhibit the essence of this "base 60" numerical system as part of its function as a cornerstone of Biblical cosmology, providing the context of the Celestial Prelude marking the birth of Christ. Additionally, it gives us a window on the "celestial mechanism" that frames all Creation, the precession of the equinoxes. This will be fully explained in the Specific signs of the Celestial Prelude. Both of these planets frame the ancient solar system as its two outer-most naked-eye planets, while opening a window on precession. It also shows a unity of Saturn's 29.5-year orbit with the 29.5-day lunar cycle on a year-day basis. This is half the Sexegesimal order of the solar system, formatted in the orbits of these two gas giants, the other half being Jupiter's near 12-year cycle spending a year in each zodiacal sign, even as the Sun spends a month in each of the 12 signs. The solar half of the order is based on a division of 60, by twelve: (12 x 5), and the lunar half by 30 [30 x 2], both multiples of sixty. This is part of the numerical order of the solar system as it was patterned by the Creator according to the phi ratio.
The Babylonian "Sar" is doubtlessly related to the Hebrew word [*H8269] of the same spelling, meaning; "prince, captain, chief, ruler, leader, head." The word has retained this meaning even in modern usage, as in the Tsar of all the Russias. As a testimony to what may have been based on the first human language, "Aesar" is a word for "God" in both, Icelandic and Irish, "Osar" in Egypt like "Osiris" was the prince. The English word "sir" and the Roman "Ceasars" are also traceable to this root. It is used in Daniel 10:13 & 20, referring the archangel Michael who dispatched the fallen angel (Daimon) who opposed the messenger angel that God sent to answer Daniel's prayer. In Isaiah 9:6, one of the great prophecies of the promised seed, it is used of the Messiah as Sar-Shalom; the Prince of Peace, the one who brings peace to all Creation [Eph. 2:11-18]. It is additionally used of Prince Moses in Exodus 2:16.
According to Hislop, The Chaldean version of this word; "Zer," meaning "to encompass" gives us not only the English basis for: "Zero signified by a circle among the Chaldeans," but also Zero; "the seed." Further, it relates to the Hebrew word zera [*H2233] used in reference to the promised seed in Genesis 3:15. To this end the Chaldean word for the "woman's promised seed" was "Zero-ashta," that also formed the basis of the name Zoroaster. We should note that in the writings of Zoroastrianism in the Zend-Avesta, the predicted return of Zoroaster as a savior who would renew all existence in preparation for the Last Judgment, was prophesied. These references to the woman's promised seed point directly to the general sign of the Celestial Prelude. Hislop also notes:
"In almost all nations, not only was a great god known under the name of Zero or Zer; the seed, and a great goddess under the name of Ashta or Ishta; the woman, but the great god Zero is frequently characterized by some epithet which implies that he is The only One." 3
This evidence provides a strong basis for a direct correlation to the decan Coma, the seed who was the desired of the nations, especially when we view the supernova in this child's head [pictured below from the Dendera zodiac] who was the promised seed, during the general sign of the Celestial Prelude. The implication that the promised seed of the woman would be the only one, speaks to the truth that Christ is the Alpha and Omega, or the first and last way God made available for the redemption of Mankind. Hislop goes on to say: "As he who by the Chaldeans was regarded as the great Seed was looked upon as the Sun incarnate, and as the emblem of the Sun was a circle, the hieroglyphic relation between zero; "the circle," and zero; "the seed" was easily established."4
The Biblical references to Christ associated with the Sun as the "light of the world," the "Sun of Righteousness" [Mal. 4:2] and in Psalm 19:4-6, are only a few of many such references. Thus, in the case of the promised seed, Zero-ashta, the religion of the Magi served as a vessel for many principles and astronomical precepts, that led Mankind to the realization of the promised seed.
Ignatius, one of the Church Fathers and the Bishop of Antioch, in about 69 AD, records that, "At the appearance of the Lord a star shone forth brighter than all other stars." If we are careful not to confuse this reference with the planet Jupiter, we can deduce that this supernova was still visible almost 200 years after it was first seen as the celestial marker of the general timeframe of Jesus' birth. Seiss has some viable historical references on this point:
"Hipparchus about one hundred twenty-five years before Christ, observed it [Coma supernova] as a new star, and was led by it to draw up his catalogue of stars. Ptolemy, about one hundred and fifty years after Christ, refers to it as having been observed by Hipparchus, but as having become so faint as hardly to be any longer discernible."5 (parenthesis and emphasis mine)
A point of interest here regarding Hipparchus is that he is generally credited with the discovery of the precession of the equinoxes, by modern science in about 134 BC. He reportedly came upon this discovery while studying the star Spica, on a celestial map produced by his predecessor, Timocharis. He noticed that Spica was about 2 degrees away from its location on the star map, and decided that it was moving an average of 1 degree every 75 years: [close to the actual 72 years]. This is a key to remember in our study of Dendera's zodiac related to Spica, and this general sign later in this study. Also during this same period referred to by Ptolemy above, shekels from Judea struck during the period of the second revolt, [132 AD.] bear the design of a bright star over the Jerusalem Temple, called Bar Kaukab, or Son of the Star. This would have also been a logical reference to the supernova that appeared in the head of the woman's son in Coma's lap, the desired of the nations, perhaps even a providential reference to Jesus as the true temple. The decan of Coma is pictured below as the three bright stars forming the inverted "L" shape, which significantly contains the North Galactic Pole, located 5 degrees west of Beta Coma. This is interesting in light of the original star picture associated with this decan, as seen in the Denderah zodiac, of a mother holding her Son in her lap, known as "the Desired of the Nations," [pictured above]. The close proximity of the Northern Galatic Pole, recalls the imagery of Cepheus "the crowned king" who regally sits astride the Celestial Pole star polaris, picturing Christ seated in the heavenlies at the right hand of the Heavenly Father [Eph. 1:20-23].
The Magi would have witnessed both this new star shining brightly in Coma, a decan of Virgo, while Jupiter was in retrograde, standing still on the Meridian in Virgo, in December of 2 BC. The general sign of our Celestial Prelude thus harmonizes with the specific signs, as the Magi headed south from Jerusalem, their visit with Herod just concluded, towards Bethlehem in search of the promised seed. This also explains why the Magi were the only group to recognize these specific celestial signs of the Messiah's birth, because the general sign was a fixture in Coma for about 200 years prior to this period. The typical person wouldn't have noticed anything out of the ordinary in the heavens, because it would not stand out unless coupled with the knowledge of the specific signs, which brought the Magi to Israel in the first place. This is another reason why the Magi were so joyful when they saw "his star," Jupiter over Bethlehem. This scenario of what the Magi beheld in the skies over Bethlehem in December of 2 BC, is depicted in the banner of this article above. In Numbers 24:17, when Jacob is referred to in Balaam's prophecy, it bears reference not only for the seed of Jacob, but also in the land promised to him as an inheritance, in his covenant with God [Gen. 15:18]. Rolleston has an interesting remark regarding this:
"The forewarned that the star must appear over Jacob, over his inheritance, would see that star in Coma passed over the center of that inheritance: but as it would also appear to pass vertically over every part of it that was nearly in the Latitude of Jerusalem, they could not at once fix on the spot of the Messiah's birth, therefore they went to inquire; the Latitude, as it were, being given by the star, the longitude by the prophecy.Magi"6
Here we see the witness of the stars, and the Scriptures, working together to bring the to the toddler Jesus, because their alert observation of "his star" brought them to Jerusalem and the scribes declaration from Micah 5:2, when Herod questioned them, sent the to Bethlehem. While en route they witnessed the heavens come alive with the proof that their historic journey was not in vain, because they saw both the Coma supernova, and Jupiter in Virgo in the same skies over Bethlehem.
In summary then, the key points regarding the general sign of the celestial prelude are first, that this supernova in Coma, set the timeframe in which the Magi were to expect the specific signs surrounding the birth of Christ. Secondly, that when this general sign is separated from the set of specific signs of Jupiter-Saturn triple conjunctions, the confusion clouding the "Star of Bethlehem," for the most part dissolves.MagiMagi
FOOTNOTES:
1 Symbols of Judaism M.A. Ouaknin p.12.
2 Sun, Moon and Earth. Robin Heath, p.28
3 The Two Babylons Hislop, p. 59
4 The Two Babylons Hislop, p. 18
5 Gospel in the Stars, Joseph Seiss. P.161.
6
http://www.try-god.com/view_page.asp?id=61
Mazzaroth; The Star of Bethlehem, Rolleston,
*Strong's Concordance word definition for H8269, H2233, etc. |
|
|
 Primer
Primer
 Anterior
2 a 9 de 9
Següent
Anterior
2 a 9 de 9
Següent
 Darrer
Darrer

|
|
|
A solar eclipse happens when the moon and sun align on a node, i.e. one of the two spots where the moon’s orbit intersects the ecliptic plane (the sun’s path through the sky). The node is called the caput draconis or “head of the dragon” and is the node that faces the sun (the tail node is on the opposite side of the earth away from the sun and is what causes lunar eclipses). These nodes are always exactly opposite one another but both move around the earth in a slow cycle of 18.618 years. When a solar eclipse occurs, the nodes are exactly aligned to the sun and the moon crosses caput draconis at the right moment causing the sun’s face to be blotted out. Then 346.62 days later, the sun will again cross that node, but the node will have moved by that time. But 346.62 days is called an eclipse year. Then 18.618 days later, the sun will cross the point where the eclipse originally occurred which will be exactly one solar year (346.62+18.618=365.24 days). Then the sun will move on to meet the moon again at its 13th and final lunation of the synodic lunar year which just happens to occur 18.618 days later (365.24+18.618=383.86 days).
In a solar year, there are 12.368 lunations (a lunation is one complete cycle of the moon’s phase changes which takes 29.53 days). The synodic lunar year lasts 13 lunations. Another type of lunar year is called sidereal and has 13 months of 27 and 28 days for a total of 354 days a year. We need to keep this in mind.
Who cares, you say? Well, before I relate it to music, I need to talk about the Golden Proportion. Not the same as the musical proportion. The Golden Proportion is defined as the point along a line that divides that line such that the shorter segment is proportional to the longer segment in exactly the same way as the longer segment is proportional to the total length of the line. This point is found at approximately 0.618 of the line’s length. This is called phi (note the lower case). The reciprocal of phi is 1/0.618=1.618 and is called Phi (note the upper case). Isn’t odd that the moon’s line of nodes swings in a complete circle in 18.618 years (and moves 19.618 days per year) thereby incorporating phi? Just coincidence? Let’s look a little further.
The eclipse year is 346.62 (or 18.618 x 18.618). The solar year later of 365.242 (18.618 x 19.618) days. The synodic lunar year 383.86 (18.618 x 20.618) days. Each is spaced apart by 18.618 days. We can construct an isosceles triangle from this. The long sides will be 19.618 units long. The vertices formed by the short side will represent the eclipse year of 346.62 days and the synodic year of 383.86 days respectively. The 3rd vertex represents earth. Dividing the short side exactly in half is where we would locate the solar year of 365.24 days. We then draw a line from that point to the earth vertex bisecting the isosceles triangle into two right-angled triangles. This line will have a length of 18.618 units. Using the Pythagorean Theorem, we can calculate the length of the short side of either right-angled triangle thusly: b2 = c2 - a2. So b2 = 19.8162 - 18.6182, hence b2 = 38.236, so the square root of b2 = 6.1835 or phi x 10! Moreover, we can now calculate the entire length of the short side of the isosceles triangle by multiplying 6.1835 by 2 to obtain 12.367, a very close approximation of the number of lunations in a solar year!
Eclipses come in families which means that certain eclipses bear certain similar characteristics with other eclipses. One of these eclipse families is called Saros, which the Chaldeans made great use of. Saros eclipses can be lunar or solar. A Saros cycle lasts about 18 years and 11 days. This is equivalent to 223 lunations or 19 eclipse years. In one eclipse year, there are 11.738 lunations. 19/11.738 = 1.618 or Phi!
As I mentioned earlier during an eclipse season, the sun encounters a lunar node once every 173.3 days. So, it takes 346.62 days for the sun to return to the same node--called an eclipse year. Coincidence that 346.62 = 18.6182? |
|
|
|
|
There are about 11 days difference between a sidereal lunar year and a solar one (354 to 365). The solar year is 12 months and the sidereal year is 13 months. The actual time differential between the two years is 10.875 days and is called the Silver Fraction or the “over-plus of the moon.” The 0.368 lunation differential is about 7/19 when expressed as a fraction and we can also call that a Silver Fraction. Now, if we draw a circle with a diameter of 13 units and then inscribe a pentagram inside that circle, the length of any of the 5 lines that make up the pentagram will be 12.364--very close to the number of lunations in a solar year. If each line represents a year, then the number of full moons in 5 years is 12.364 x 5 or 61.82 full moons--phi x 100!!
This brings us to the Pythagorean right triangle. Since the solar year is 12 months and the lunar year is 13 months, we find a unique way to wed the two. The male marriage number in Pythagoreanism is 5 because it adds the female 2 to the male 3. A triangle with a base of 12 and a side of 5 will have a hypotenuse of 13 using the Pythagorean Theorem. If we divide the 5 into segments of 2 and 3, we can calculate a new hypotenuse--122+32=153 (review the fish story in the last chapter of the Gospel of John) and the square root of 153 is 12.369, a very close approximation of the number of lunations in a solar year!
In a musical scale--easiest to see on a keyboard--there are 12 half-steps in an octave which consists of 8 notes (white keys) separated by 5 black keys (designated sharps or flats as the case may be) and 8+5=13. The 5 black keys are also separated into a group of 2 and a group of 3! Moreover, 3 and 2 form the ratio for the Perfect 5th interval which consists of 5 notes covered in 7 half-steps.
Mathematically, we count calculate the perfect 4th as (2AB)/(A+B) where A=6 and B=12. We call this the harmonic mean. We calculate the perfect 5th as (A+B)/2 and we call this the arithmetic mean. So, the musical proportion is expressed mathematically as A:(2AB)/(A+B)=(A+B)/2:B
The Pythagorean whole tone 8/9 can also be expressed as 0.888 and Iesous or Jesus has gematria value of 888. The perfect 5th is 2/3 and that is 0.666 and 666 is the number of the sun. If A=353 (Hermes) and B=1061 (Apollo), then the harmonic mean is of (2AB)/(A+B)=531 and 531 is the gematria value of LYRA or lyre. The Greek mythology, Hermes made the lyre from a tortoise shell and presented it to his brother Apollo. The Greeks were demonstrating a harmonic relationship literally. If we use the same two numbers to calculate the arithmetic mean, it would be 1414/2=707. 1414 is the gematria value of THE GOD PYTIAS in Greek and also the value of the square root of 2 or 1.414. 707 is the value of THE GOD HERMES and is the inverse of the square root of 2 or 0.707.
Between the perfect 4th and 5th exists the geometric mean (the tritone) and it is calculated as the square root of AxB. The square root of 353x1061 is 612, the gematria value of ZEUS.
From C to G is a perfect 5th and the frequency of F-sharp is a tritone of 6 half-steps and represents the geometric mean. Its frequency is 1415 (THE GOD APOLLO) cycles (the square root of 2 is 1.414). The string is divided at that point into 0.707 (THE GOD HERMES) of its original length (the inverse of the square root of 2 is 0.707).
The string ratio between the octave and the perfect 4th is 0.612 (ZEUS) and between the geometric mean and the prefect 5th 0.815 (ZOE or life). The frequency between the open string and the perfect 5th is 1224 cycles and 1224 is FISHES and THE NET. Dividing the geometric mean by the harmonic mean produces a ratio of 1.061 (APOLLO). Dividing the harmonic mean and the arithmetic mean produces 0.888 (JESUS).
12+1--the full octave is Jesus and his 12 disciples or the sun in the middle of the zodiac is expressed in music as the C maj/A min scale from which proceed the other 12 major and minor scales. Also the octave interval which has a highest and lowest tone of the same note (alpha and omega) is the central interval around which the other 12 are derived. On a guitar fretboard, the string is divided into 12 parts to get up to an octave and the string played open is the central tone which these other 12 are derived.
http://forums.about.com/n/pfx/forum.aspx?tsn=3&nav=messages&webtag=ab-clasiclmusic&tid=817 |
|
|
|
|
SCALES
Every scale is 8 notes. Starting at any key of the keyboard and counting up 8 notes, one plays either in a major scale (sounds happy) or a minor scale (sounds sad or haunting) as follows:
123-4567-8 major scale
12-345-678 minor scale
The dashes between the numbers indicate a half-step. The other numbers are whole steps apart.
Below is a list, which should be considered circular, of all the keys in the Western scales arranged in what is known as the circle of 5ths. C major is the central scale. Its corresponding minor scale, called an enharmonic equivalent, is the A minor scale. Starting at C major, each even-numbered scale moves up by a perfect 5th (7 half-steps) interval. Every odd-numbered scale is a perfect 5th down from C major/A minor. So, the G-major scale starts at the G key on the keyboard which is a perfect 5th up from C and one would count up 8 notes using the major scale numerical representation shown above. Counting a perfect 5th up from the G key puts one the D key and the major scale numerical representation is again employed to obtain the D major scale. Counting down a perfect 5th from C will put one at the F and the same major scale model is employed. A perfect 5th down from F is B-flat. And so on.
Minor scales are tuned a minor 3rd down from their enharmonic equivalents. A is a minor 3rd down from C, so A minor is the enharmonic equivalent of C major and vice-versa. Like major scales, minor scales are tuned perfect 5ths apart:
Circle of 5ths
C maj
A min
1. F maj
D min
2. G maj
E min
3. B-flat maj
G min
4. D maj
B min
5. E-flat maj
C min
6. A maj
F-sharp min
7. A-flat maj
F min
8. E maj
C-sharp min
9. D-flat maj
B-flat min
10. B maj
G-sharp min
11. G-flat maj
E-flat min
12. F-sharp maj
D-sharp min |
|
|
|
|
To give an example of how a major an minor scale are determined, it is easiest to use a keyboard. The easiest scale is C major. Start at the C key then go up a whole step to D then another whole step to E but then a half-step to F (there is no intervening black key between E and F or between B and C but both sets of notes are still only a half-step apart) then another whole step to G then another to A then another to B and finally a half-step to C. So the progression looks as such: C D E F G A B C. With A minor, we start at A and move a whole step to B then a half-step to C and so on. The progression is A B C D E F G A. Note that there are no sharps or flats (no black keys) in either scale.
Let’s try one a little harder. How about D-flat major/B-flat minor? Okay. For the major scale, we start at D-flat (the black key between C and D) and go up a whole step to E-flat then another whole step to F but then a half-step to G-flat and so on. The progression is as follows: D-flat/E-flat/F/G-flat/A-flat/B-flat/C/D-flat. The B-flat minor scale progression then is B-flat/C/D-flat/E-flat/F/G-flat/A-flat/B-flat. When determining the notes of a scale, notice that the notes always go in order. We don’t go from C to C-sharp in the same scale but rather C to D-flat even though C-sharp and D-flat are the same black key. The reason why is obvious when one looks at the notation on a piece of sheet music. Sharps and flats are never mixed in the same scale.
Notice that both major and equivalent minor scales use the identical notes in the same progression. The only difference is the starting point. Yet one sounds happy and the other sad or grand and melancholy as the case may be. The same with intervals; a perfect 5th up from C is G, but a perfect 4th down from C is also G. The same two notes and yet they are two different intervals. There are also augmented and diminished intervals as well as double and triple sharps and flats but we are not concerned with these here.
The interesting thing about octaves are that they seem to be universal in music. In the music theory of India, a scale consists of seven notes and the eighth repeats. Octaves are associated with 8 but should also be understood as 7+1. Even the Chinese pentatonic scale actually has seven notes but two are not played and used only in theory and the eighth note repeats. Octaves appear in the electromagnetic spectrum (seven primary colors of visible light), the periodic table of elements (seven groups of elements), the planet Venus tracks through sky in an 8-year cycle. The original eight cells that we form from remain at the base of the spine and is sometimes called the egg of life.
Chords are intervals of three or more notes played simultaneously and are generally considered harmonic. Perhaps the most common is the C major chord consisting of C E G and the next higher C. E is a major 3rd above C while G is a perfect 5th above C while high C is a full octave above low C. So Pythagoras’s musical proportion of 6:8::9:12 is expressed in this chord. Notice also that the number of half-steps from C to E is 4, from E to G is 3 and from G to high C is 5. The numbers 3, 4 and 5 remind us irrepressibly of the right-angled triangle made so famous by the Pythagoreans. If one side is 4 units long and another is 3 then the hypotenuse (or diagonal) will be 5. The perimeter of the triangle is 3+4+5=12, the full octave. So the perfection of the 3-4-5 triangle is the visual equivalent of the harmonious C major chord. |
|
|
|
|
The diatonic scale consists of 7 notes. The word “diatonic” is Greek for “across the tones.” It is different than the chromatic scale which has 12 notes. The chromatic scale hints at the association of music and color (after all, we speak of “tone-coloring” for proper musical mood) since “chromatic” means comes from the Greek “khromos” or “color.” The physicist Hermann von Helmholtz classified colors and notes as follows:
- G ultraviolet
- F, F# violet
- E indigo blue
- D# cyanogen blue
- D greenish blue
- C# green
- C yellow
- A# orange-red
- G#, A red
- G infrared
12 and 7 have other links. Again, astronomy provided ancient peoples with 7 planets moving through 12 signs of the zodiac. The Greeks had 12 gods represented on earth by 7 wise men. The Chinese had their 7 Sages of the Bamboo Grove. Druids similarly had 7 sages in their oak groves as well. When the 7 notes of the diatonic scale are combined with the five notes of the pentatonic scale (used by Polynesians and Scots as well as the Chinese), we get the chromatic scale.
Musical staff lines are a convention credited to Guido d’Arezzo sometime around 1000 CE. He also came up with DO-RE-MI-FA-SOL-LA-TI-DO. However, he didn’t use “TI” but “SI” (where do you think square-dancers get the “doe-see-doe” from?). What did these consonant-vowel combinations mean? As I said, music theory was originally a form of astronomy/religion: DOminus (Lord, divinity), REgina Cœli (Queen of Heaven, the moon), MIcrocosmos (the small universe, the earth), FAta (fate, the planets as used for divination), SOL (obviously the sun), LActea (milk, of course, meaning the Milky Way), SIder (star), DOminus (Lord, divinity). D’Arezzo’s scale structure is the Gnostic ladder of Creation. The Absolute manifests as both the biggest which contains everything and works its way down hierarchically to the smallest which is contained in everything each mirroring the other—macrocosm and microcosm.
Music was considered by ancient peoples to be an expression of the Absolute of the universe, its vibrations meant to stir our emotions and alter our moods. Musical harmony was thought of as an expression of the interaction of the hierarchies of heaven and earth. There were seven such steps on the ladder as per the diatonic scale (if you’re wondering if this might be the meaning of Jacob’s Ladder, yes). The lower level acted as soil for the higher level which sprouted from it. The lower was the embodying principle of the soul above and the upper was the ensouling principle of the body beneath. The vibrating string represented the archetypal structure as it resonated between manifest and unmanifest, between hidden and exposed, between harmony and discord, between positive and negative. This we see as duality that characterizes existence (e.g. light/dark, male/female, good/evil, spirit/matter, etc.) or what the Pythagoreans called the Dyad. The vibrating string is the symbol of creation (in physics today there is even String Theory and Super String Theory which holds that matter is composed of tiny vibrating “strings”—strange, isn’t it?).
http://forums.about.com/n/pfx/forum.aspx?tsn=3&nav=messages&webtag=ab-clasiclmusic&tid=817 |
|
|
|
|
miércoles, 4 de mayo de 2011
Judá ben Samuel de Regensburg (1140 – 1217) fue un rabino judío alemán que, antes de su muerte en 1217 d.C., supuestamente profetizó sobre la nación de Israel.
Ben Samuel habría profetizado que el Imperio Turco Otomano reinaría sobre la Ciudad Santa de Jerusalén por ocho jubileos (8 x 50 = 400 años). Un jubileo es un periodo de 50 años de acuerdo con Levítico 25:8-13. Por lo tanto, ocho jubileos serían el equivalente a 400 años.
Aparentemente de acuerdo a lo previsto por ben Samuel, 300 años después(1517) los turcos del Imperio Otomano tomaron el control de Jerusalén y la dominaron por los próximos 400 años. Ellos fueron finalmente expulsados de la Tierra Santa en 1917 por las fuerzas aliadas, bajo el comando del General George Allenby, sin que ningún tiro fuese disparado. La profecía del rabino en relación al periodo de 400 años aparentemente se cumplió con exactitud.
El rabino también habría profetizado que en el noveno jubileo (450 años a ser contados a partir de la invasión turca en 1517) Jerusalén se volvería una "tierra de nadie". Esto ocurrió entre 1917 y 1967, debido al hecho de que Jerusalén fue colocada bajo el dominio del Mando Británico en 1917 por la Liga de las Naciones y literalmente no pertenecía a ninguna nación.
Aún después de la Guerra de la Independencia de Israel (1948-49), Jerusalén todavía estaba dividida por una franja de tierra que cortaba el corazón de la ciudad, separando el dominio de Jordania (al este) del dominio israelí (al oeste). La franja de Jerusalén era llamada "la tierra de nadie" tanto por los israelíes como por los jordanos. Cualquier persona que atravesara esta franja era ametrallada.
Esto cambió solamente después de la Guerra de los Seis Días, cuando toda la parte este de Jerusalén fue conquistada por tropas israelíes y toda la ciudad pasó a estar bajo el dominio de Israel. Aparentemente, una vez más la profecía hecha por el rabino se cumplió con exactitud 750 años después de su muerte.
Supuestamente, el rabino, también profetizó que en el décimo jubileo (10 x 50 = 500 años a ser contados a partir de la invasión turca en 1517, o sea en 2017), Jerusalén volvería a estar bajo el dominio de los judíos después de mas de dos milenios de diáspora judaica, y el reinado mesiánico se iniciaría al final de este período. El décimo jubileo se inició en 1967 y terminará en el 2017.
Informaciones adicionales
Judá ben Samuel es conocido entre los judíos como Yehuda HeHasid (Judá el Piadoso). Fue el fundador de un movimiento judío en el siglo XII conocido como Hasidei Ashkenaz (Literalmente "Los Piadosos de Alemania") que enfatizaba la oración y la práctica de una conducta moral y piadosa.
Las enseñanzas de ben Samuel fueron a veces causa de controversia en las sinagogas. Para algunos en la comunidad judaica, ben Samuel era un místico cabalista. Su énfasis en la oración fue vista por algunos de la comunidad judaica como exagerada y en detrimento del estudio. Según la Enciclopedia Judaica, fue conocido como un piadoso en su tiempo y alguien que enseñaba que el estudio de las Escrituras Sagradas era más importante que el estudio del Talmud.
Judá ben Samuel es sin duda una figura controvertida entre los estudiosos judíos, que le atribuyen la introducción de la teosofía entre los judíos en Alemania. Debemos observar, sin embargo, que ya en el siglo XII ben Samuel predicaba el mensaje "evangélico" de una relación personal entre el hombre y su Creador - un concepto "inconsistente con la naturaleza divina" par los judíos y, por lo tanto, un mensaje "hereje" que le ganó la antipatía de muchos de sus contemporáneos.
Cronología de los Jubileos: cada 49 o 50 años?
Los jubileos se cuentan a cada 50 y no a cada 49 años como algunos los cuentan, encimando el año 50 de un jubileo con el primer año del siguiente. Lev 25:11 El año cincuenta os será jubileo; no sembraréis, ni segaréis lo que naciere de suyo en la tierra, ni vendimiaréis sus viñedos, Lev 25:12 porque es jubileo; santo será a vosotros; el producto de la tierra comeréis.
En Lev 25:20-22 se refiere solo a las semanas de años: "Y si dijereis: ¿Qué comeremos el séptimo año? He aquí no hemos de sembrar, ni hemos de recoger nuestros frutos; entonces yo os enviaré mi bendición el sexto año, y ella hará que haya fruto por tres años. Y sembraréis el año octavo (el año 1 del siguiente ciclo), y comeréis del fruto añejo; hasta el año noveno (año 2 del siguiente ciclo de 7 años), hasta que venga su fruto, comeréis del añejo."
Si contamos jubileos de 49 años, o sea, encimando el año 50 de un jubileo con el primer año del siguiente jubileo, entonces se sembraría también en el año del jubileo que es el año octavo de ese ciclo o 1 del siguiente ciclo. En el jubileo o año octavo del último ciclo es el año 50 donde no se siembra, solo se siembra el año 1 del siguiente ciclo.
De no contarse así, solo se sembraría el año 2 y se cosecharía recién al año 3 del siguiente ciclo de 7 años. Esto contradice la torah en el siguiente versículo: Lev 25:3 Seis años sembrarás tu tierra, y seis años podarás tu viña y recogerás sus frutos (Porque no se podrían, en el ciclo de 7 años que sigue a un año jubileo, podar la viña y recoger los frutos o sembrarlos durante seis años porque faltaría un año ocupado por el último jubileo según los que cuentan los jubileos encimando el año 50 con el año 1).
Esto quiere decir que tanto el Libro de los Jubileos como el Libro de Enoc (Apócrifos) calculan mal los jubileos, pero esto no es de extrañar, ya que los cálculos de los años según la cronología del Libro de los Jubileos probablemente está equivocada, al inicio concuerda con los relatos de Génesis, pero en el diluvio ya se desfasa en más de 200 años.
Consideraciones finales
De acuerdo a Levítico 25, la nación de Israel es reunida con su tierra en el año del Jubileo. Por esta razón el año del Jubileo juega un papel importante en la historia de Israel.
Atención a las palabras "supuestamente" y "aparentemente" utilizadas en este artículo. No podemos afirmar sobre las creencias de ben Samuel (si era o no cabalista) y tampoco sabemos si esta profecía es real o si fue fabricada después de los acontecimientos históricos relatados arriba.
También debemos recordar que cualquier “profecía” de origen extra-bíblico debe ser tomada con suma cautela, y sabiendo que únicamente la Palabra de Dios es la palabra profética que cuenta con el completo respaldo de Dios. Cualquier otra palabra profética debe ser evaluada a la luz de la Palabra de Dios, la cual es la única que es la lumbrera en el camino de la Iglesia. Este reporte de la profecía de este rabino alemán es sumamente curioso, sobre todo por su simplicidad y aparente exactitud histórica.
La biblia afirma claramente que el Reino vendrá. Será en el 2017? Podrá ser antes? Podrá ser después? No lo sabemos. Pero cuando Yeshúa nos enseñó a orar: "Venga a nosotros Tu Reino" es porque el vendrá, y todo indica que estamos próximos a ese Gran Día! Maranatha!
Shalom
Fuentes:http://issuu.com/ryaninzion/docs/israel_today_march_2008/18 Ver Página 18: Israel: Between Mysticism and Reality http://diasdenoe.wordpress.com/2011/05/01/la-profecia-de-los-jubileos-serie-%C2%BFcuan-cerca-estamos-del-fin-parte-3/ http://paoevinho.wordpress.com/2011/01/05/a-profecia-de-juda-ben-samuel/http://paoevinho.org/?p=6238http://shalom-israel-shalom.blogspot.com/2011/01/2017-vinda-do-reino.htmlhttp://2010rapture.org/8jubilees.htmlhttp://watchfortheday.org/http://en.wikipedia.org/wiki/Judah_Ben_Samuel_of_Regensburg knew the exact year of Israel's redemption
|
|
|
|
|
. Juan 16:21 La mujer cuando da a luz, tiene dolor, porque ha llegado su HORA; pero después que ha dado a luz un niño, ya no se acuerda de la angustia, por el gozo de que haya nacido un hombre en el mundo.
|
|
|
|
|
|
|
|
DAN/ DINERO / TRANSFIGURACION DE CRISTO / SERPIENTE / $$$$$$$$
12 TRIBUS/ 12 APOSTOLES / 12 HORAS / TIEMPO
$=TRASLACION EN EL TIEMPO
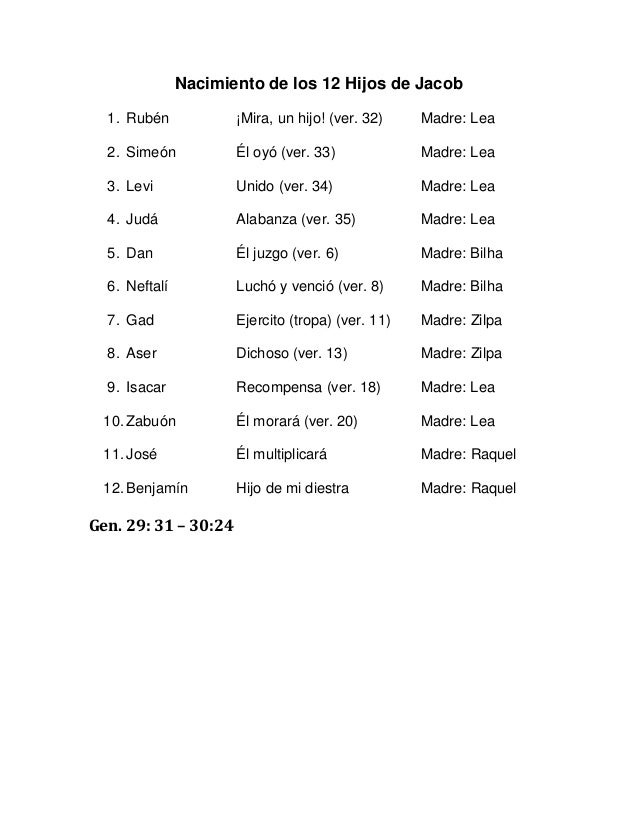
13 HIJOS MAS DINA, LA UNICA HIJA MUJER
JABOB=ISRAEL=VENCEDOR
|
|
|
|
|
|
 Primer
Primer
 Anterior
2 a 9 de 9
Següent
Anterior
2 a 9 de 9
Següent
 Darrer
Darrer

|