
Publicidad del 10º aniversario en el 2011. Lo mismo, espirales encriptadas, estrella 8 puntas
Para mejor apreciación, la obra completa
 |
Click para ampliar |

[/QUOTE]
El cono - Ingles C-ONE por lo tanto 3 - 1 coordenadas Piscis -Acuario
Vamos a ver que encripta el cono

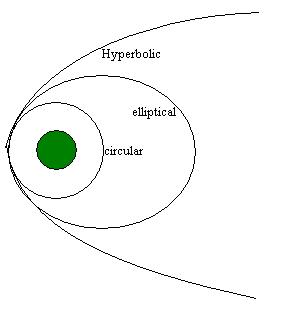
Se denomina sección cónica (o simplemente cónica) a todas las curvas intersección entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en tres tipos: elipse, parábola e hipérbola. un cono circular recto de dos hojas con un plano que no pasa por su vértice.
Donde econtramos esta geometria ? En las orbitas
La excentricidad de la órbita de un cuerpo astronómico es el importe por el que su órbita se desvía de un perfecto círculo , donde 0 es perfectamente circular, y 1.0 es una parábola , y ya no es una órbita cerrada. Su nombre se deriva de los parámetros de las secciones cónicas , ya que cada órbita de Kepler es una sección cónica.

Una órbita elíptica de Kepler con una excentricidad de 0,7 (rojo), una órbita parabólica de Kepler (verde) y una órbita de Kepler hiperbólica con una excentricidad de 1,3 (azul)
Variacion de las orbitas segun la variable excentricidad

Hablamos de las anomalias de la Luna, especificamente la variacion de su excentricidad.
La excentricidad de la Tierra órbita 's es actualmente de unos 0,0167; la órbita de la Tierra es casi circular. Durante cientos de miles de años, la excentricidad de la órbita de la Tierra varía de cerca de 0,0034 a casi 0.058 como resultado de las atracciones gravitacionales entre los planetas (ver gráfico ). [ 1 ]
En otros valores, Mercurio (con una excentricidad de 0.2056) ostenta el título como el mayor valor entre los planetas del Sistema Solar. Antes de la redefinición de su estatus de planeta , Plutón, celebrada este título con una excentricidad de alrededor de 0,248. La Luna valor 's es 0,0549. Para los valores de todos los planetas en una tabla, consulte la lista de los objetos gravitacionalmente redondeadas del Sistema Solar .
La mayor parte del Sistema Solar asteroides tienen excentricidades entre 0 y 0,35 con un valor promedio de 0,17. [ 2 ] Sus excentricidades son relativamente altos debido probablemente a la influencia de Júpiter y de colisiones pasadas.
La excentricidad de los cometas con mayor frecuencia cerca de la 1. cometas periódicos tienen muy excéntricas órbitas elípticas , con excentricidades justo por debajo de 1; el cometa Halley órbita 's elíptica, por ejemplo, tiene un valor de 0,967. Los cometas no periódicos siguen casi parabólicas órbitas y por lo tanto tienen excentricidades muy cercano a 1. Los ejemplos incluyen el cometa Hale-Bopp , con un valor de 0,995 [ 3 ] y el cometa C/2006 P1 (McNaught), con un valor de 1,000019. [ 4 ] Como el valor del Hale-Bopp es menor que 1, su órbita es elíptica, por lo que el cometa la voluntad a cambio de los hechos. [ 3 ] El cometa McNaught tiene una órbita hiperbólica , mientras que dentro de la influencia de los planetas, pero todavía está vinculado con el Sol con un periodo orbital de unos 10 ^ 5 años. [ 5 ] A partir de 2010 una época , el cometa C/1980 E1 tiene la mayor excentricidad de cualquier cometa conocido hiperbólica con una excentricidad de 1,057, [ 6 ] y dejar el sistema solar de forma indefinida.
Neptuno 's la mayor luna de Tritón tiene una excentricidad de 1,6 x 10 -5 [ 7 ] , que es la más pequeña excentricidad de cualquier organismo conocido en el Sistema Solar, su órbita es tan cercana a un círculo perfecto como se mide actualmente.
 |
Click para ampliar |

El mon-g-e visco y pelado codigo del huevo
Que es lo que sucede ?
Mercurio es el planeta 1 codigo mon, tiene mayor velocidad de precesion por lo tanto mayor excentricidad codigo que podemos ver por ejemplo en los comics de X Men, o sea los hombre de la cruz a 60 grados.
La ley de Newton de precesion eliptica orbital no se ajusta a Mercurio y no pudo ser explicada aun, oficialmente se pretende explicar con la teoria de la relatividad por la deformacion del espacio.
Pero nosotros como sabemos que el planeta mercurio es un fractal dependiente del centro de la galaxia, podemos entender que su velocidad se debe a su interdependencia directa al centro al igual que nuestra Luna - mon, o Urano el espejo cuyo eje se encuentra a 60 grados.

Quick silver - plata ligera es el nombre alquimico del mercurio
Por lo tanto a mayor velocidad mayor excentricidad
De continuar incrementando la velocidad en la medida que el espiral del tiempo se achica en el centro de la galaxia, la excentricidad aumenta hasta llegar por ejemplo a la parabola tridente de Newton.
1911 Encyclopædia Britannica/Parabola - Wikisource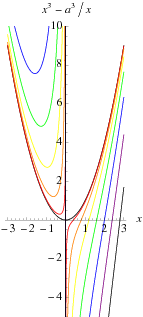
La parábola cartesiano es una curva cúbica que también se conoce como el tridente de Newton a causa de su triple forma. Su ecuación es xy = $ ³ $ ax + bx ² + cx + d , y se compone de dos patas asintóticas al eje de Y y dos patas parabólicos (fig. 3). La forma más simple es axy = x ³-³ , en este caso la posición de serpentina muestra en la figura degenera en un punto de inflexión. Descartes utilizó la curva para resolver ecuaciones séxtica mediante la determinación de sus intersecciones con un círculo, construcciones mecánicas estuvieron a cargo de Descartes ( Geometría , lib 3.) y Maclaurm ( Orgánica Geométrica ).
 |
Click para ampliar |


Habiamos visto la progresion geometrica del hojo de Horus
La disección del segmento parabólico

La disección de Arquímedes de un segmento parabólico en triángulos infinitos.
La idea principal de la prueba es la disección del segmento parabólico en triángulos infinitos, como se muestra en la figura de la derecha. Cada uno de estos triángulos está inscrito en su propio segmento parabólico de la misma manera que el triángulo azul se inscribe en el segmento de gran tamaño.
Las áreas de los triángulos
En las proposiciones dieciocho y veintiún años, Arquímedes demuestra que el área de cada triángulo verde es una octava parte del área del triángulo azul. Desde el punto de vista moderno, esto es porque el triángulo verde tiene la mitad de la anchura y un cuarto de la altura: [ 1 ]
Por extensión, cada uno de los triángulos amarillos tiene un octavo del área de un triángulo verde, cada uno de los triángulos rojos tiene un octavo del área de un triángulo de color amarillo, y así sucesivamente. Utilizando el método de agotamiento , se deduce que la superficie total del segmento parabólico está dada por

Aquí T representa el área del triángulo azul grande, el segundo término representa el área total de los dos triángulos verdes, el tercer término representa el área total de las cuatro triángulos amarillos, y así sucesivamente. Esto simplifica para dar

Suma de serie
Para completar la demostración, Arquímedes muestra que
La expresión de la izquierda es una serie geométrica , cada término sucesivo es una cuarta parte de la anterior legislatura. En las matemáticas modernas, la fórmula anterior es un caso especial de la fórmula de la suma de una serie geométrica .
Arquímedes se evalúa la suma usando un método enteramente geométrico, [ 2 ] se muestra en el cuadro a la derecha. Esta imagen muestra un cuadrado unidad que se ha dividido en una infinidad de pequeños cuadrados. Cada cuadrado púrpura sucesivo tiene un cuarto de la zona de la plaza anterior, con el área total de púrpura a la suma
Sin embargo, los cuadrados de color púrpura son congruentes a alguno de los conjuntos de cuadrados de color amarillo, y así cubrir 1/3 del área del cuadrado de la unidad. De ello se deduce que la serie anterior sumas de 4/3.

Prueba de Arquímedes que 1 + 1/4 + 1/16 + 1/64 + ... = 4/3
Esta serie geometrica es un claro fractal, o sea se repiten el patron geometrico inicial disminuyendo el tamaño x 2 sucesivamente.

