De Wikipedia, la enciclopedia libre
En matemática, una n-esfera (o hiperesfera) es la generalización de la «esfera» a un espacio euclídeo de dimensión arbitraria. En otras palabras, la n-esfera es una hipersuperficie del espacio euclídeo  , notada en general
, notada en general  . Constituye uno de los ejemplos más sencillos de variedad matemática.
. Constituye uno de los ejemplos más sencillos de variedad matemática.
Dado un espacio euclídeo E de dimensión n+1, A un punto de E, y R un número real estrictamente positivo, se le llama hiperesfera de centro A y radio R al conjunto de puntos M tales que su distancia a A vale exactamente R.
La n+1-tupla de puntos (x1,x2,…,xn+1) que están en una n-esfera (Sn) se representa con la ecuación:
 ,
,
donde el centro es el origen de coordenadas O (0,0,...,0)[1]
Ejemplos:
- Para n=0, la hiperesfera consta de dos puntos de coordenadas R y -R.
- Para n=1, la hiperesfera es una circunferencia.
- Para n=2, la hiperesfera es la esfera usual.
Ecuación de una hiperesfera[editar]
Teniendo como datos un punto fijo 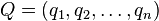 llamado centro y el radio R, real positivo, siendo
llamado centro y el radio R, real positivo, siendo 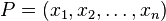 un cualquiera de la hiperesfera, la ecuación correspondiente es,[2] [3]
un cualquiera de la hiperesfera, la ecuación correspondiente es,[2] [3]

O también en forma vectorial, la esfera de radio R y centro w en E es el conjunto de todos los puntos x que cumplen
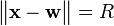
Propiedades[editar]
El volumen del espacio delimitado por una hiperesfera de dimensión n-1 y de radio R, que es una bola euclídea de dimensión n, vale:
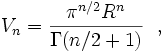 (1)
(1)
donde  es la función gamma.
es la función gamma.
Notar la siguiente particularidad:  tiende a cero cuando n tiende a infinito.
tiende a cero cuando n tiende a infinito.
El volumen de una hiperfesfera, de radio R, en el espacio cuadridimensional aplicando la formula (1) para n = 4 resulta
- V4 = π2R4 /2
y aplicando[4] la fórmula Γ(x + 1) = x Γ ( x )
El espacio encerrado por una (n-1)-esfera es una n-bola. Una n-bola es cerrada si incluye la n-esfera y abierta en caso contrario.
Ejemplos:
- La 1-bola es un segmento de recta, el interior de una 0-esfera.
- La 2-bola es un disco, el interior de un círculo (1-esfera).
- La 3-bola es la bola ordinaria, el interior de una esfera (2-esfera).
Véase también[editar]
Referencias[editar]
http://es.wikipedia.org/wiki/N-esfera 
