|
Réponse |
Message 1 de 23 de ce thème |
|
| Tanto el Tabernáculo y el Templo consistían de tres partes: |
| |
El Atrio |
El Lugar Santo |
El Lugar Santísimo |
|
Con relación al Tabernáculo
|
| |
El Lugar Santísimo era un cubo (10 pies x 10 pies x 10 pies) |
|
Con relación al Templo:
|
| |
El Lugar Santísimo era un cubo (20 pies x 20 pies x 20 pies) |
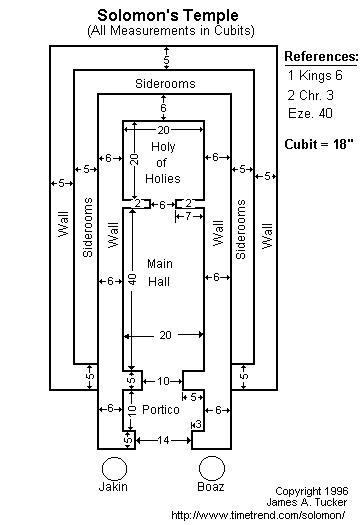
El tabernáculo propiamente dicho era una tienda cuadrangular, de 30 codos* de
largo, 10 de ancho y 10 de alto. Las dimensiones del conjunto de la estructura
no figuran con exactitud en los registros del Exodo, pero se las puede calcular
sobre la base de los detalles que se dan de las cortinas y las tablas que se
usaron en las paredes del tabernáculo, y de las medidas proporcionales, pero
mayores, del templo de Salomón (1 R. 6:2). La tienda estaba dividida en 2
compartimentos: el 1º conocido como "lugar santo" (Ex. 28:29), y el 2º como
"lugar santísimo", literalmente "el Santo de los Santos" (26:33, BJ). Este
constituía un cubo de 10 codos por lado, mientras el lugar santo era de 10
codos por 20. El tabernáculo estaba rodeado por un atrio o patio de 50 codos
de ancho por 100 de largo, limitado por cortinas de lino de 5 codos de alto
(27:18). Esta pared de cortinas estaba suspendida por 60 columnas, quizá de
maderas de acacia* (por ser esta la madera usada para los muebles y otras
columnas; cf 26:37) revestidas de plata y sostenidas por pedestales de bronce.
En la parte central del extremo oriental del patio se hallaba la entrada, que
estaba constituida por una cortina especial de 20 codos de largo (27:9-17). En
la mitad oriental del patio, cerca de la entrada, estaba el altar de los
holocaustos (vs 1-8) y el lavacro o lavatorio (30:17-21).
Leer más: Diccionario Biblico Cristiano Online y Gratis en Español - Significado o definicion de Tabernaculo
EL LUGAR SANTISIMO DEL TEMPLO DE SALOMON Y DEL TABERNACULO DE MOISES TENIA FORMA DE CUBO Y ESTABA ORIENTADO DE ESTE A OESTE. CONCRETAMENTE DICHO COMPARTIMENTO ESTABA HACIA ADONDE SALE LA LUNA CRECIENTE. ESTO EXPLICA SU FUERTE NEXO CIENTIFICO CON DICHA LUNA, INTERRELACIONADA CON EL NACIMIENTO DE UN NIÑO. LA LUNA CRECIENTE TIENE LA CUALIDAD DE QUE SALE Y SE PONE A LA PUESTA DEL SOL SIEMPRE EN EL OESTE. CONCRETAMENTE EL MENSAJE ESPIRITUAL DEL LUGAR SANTISIMO DEL TABERNACULO DE MOISES Y DEL TEMPLO DE SALOMON TIENE UN FUERTE NEXO, INSISTO CON EL NACIMIENTO DE UN NIÑO, Y MAXIME QUE EN EL CONTEXTO A LOS MESES DEL AÑO EL OESTE NOS CAE EN SEPTIEMBRE U OCTUBRE, OSEA EN LA FIESTA DE LOS TABERNACULOS. TABERNA/VINO/GRIAL
Si usted mira objetivamente el cubo vera que esta relacionado con el NUMERO 6 (6 SUPERFICIES), 12 (LINEAS PERIMETRALES/12 MESES LUNARES), NUMERO 8 (PUNTOS PERIMETRALES/RESURRECCION) E INCLUSO CON EL NUMERO 28 CONSIDERANDO LAS LINEAS DIAGONALES INCLUIDAS LAS INTERIORES. CONCRETAMENTE EL CUBO ESTA DISEÑADO EN FUNCION EL MES LUNAR CON LOS SABADOS LUNARES.
INCLUSO TAMBIEN LE VEMOS AL CUBO UN NEXO ZODIACAL Y GALACTICO EN EL CONTEXTO A LOS EXTREMOS DEL ZODIACO SEGUN APOCALIPSIS 4:7
HIPERCUBO
SI CONTAMOS LA CANTIDAD DE PARTES DEL CUBO MAGICO TENEMOS EL ASOMBROSO NUMERO 26 RELACIONADO CON LA GEMATRIA EN EL HEBREO DE YHWH E INCLUSO EN EL INGLES DE GOD/DIOS.
| god in Simple Gematria Equals: 26 |
( |
g
7 |
o
15 |
d
4 |
) |
APOCALIPSIS 21
15. El que hablaba conmigo tenía una caña de medir, de oro, para medir la ciudad, sus puertas y su muro.
16. La ciudad se halla establecida en cuadro, y su longitud es igual a su anchura; y él midió la ciudad con la caña, doce mil estadios; la longitud, la altura y la anchura de ella son iguales.
17. Y midió su muro, ciento cuarenta y cuatro codos, de medida de hombre, la cual es de ángel.
|
|
|
|
Réponse |
Message 2 de 23 de ce thème |
|
|
|
|
Réponse |
Message 3 de 23 de ce thème |
|
NUMERO 8 (SEXTO NUMERO DE LA SERIE DE FIBONACCI) / RESURRECCION DE CRISTO /ISHTAR/ EAST STAR /ESTRELLA DEL ORIENTE
DAVID
VID/VINO/GRIAL
VIDA
MARIA MAGDALENA UBICADA, DESDE LA ISQUIERDA DEL SEÑOR, EN EL OCTAVO LUGAR
Everything is Connected and there are no
coincidences
|
|
|
|
Réponse |
Message 4 de 23 de ce thème |
|
NUMERO 322/ 8 DIVISORES/ NUMERO 8/ RESURRECCION/ LUGAR SANTISIMO/ CUBO/ NUMERO DE ORO PHI/ NUMERO 23 / SIRIO / ESTADOS UNIDOS / KABA (ISLAM) / 911
Divisors of the Number 322
- 322 has 8 positive divisors: 1, 2, 7, 14, 23, 46, 161, 322
- The sum of the positive divisors is 576
- 322 has 7 proper divisors: 1, 2, 7, 14, 23, 46, 161
- The sum of the proper divisors is 254
- 322 is a deficient number since the sum of the proper divisors is less than 322
- 322 is not a perfect number
- 322 is not an abundant number
|
|
|
|
Réponse |
Message 5 de 23 de ce thème |
|
EL HIPERCUBO ESTA INTERRELACIONADO KAVALISTICAMENTE CON EL NUMERO 19 (CONTEXTO AL NUMERO 6/EXAGONAL Y AL NUMERO 8/OCTOGONAL)-SHABBAT ES OCTAVO DIA
Metatron's Cube
|
Metatron's Cube is usually presented as thirteen circles and the lines that connect the middles of those. When you look at this image, the eye is first presented with hexagons and hexagrams; then with triangles and rectangles.
Note that the figure depicts the "six directions in space" (3 dark lines), and is essentially an expansion (by adding six circles) of the Star of David, located at the center. Note especially that the Star of David consists of seven points, although the center point is seldom emphasized. The Cube is a depiction of 12 around 1 like the disciples or the 12 tribes, the labors of Hercules and the zodiac signs.

The Cube is easier to see if we fill in six more circles. Note that adding the Pythagorean "Y" to the hexagon yields three rhombus, which is how we depict a 3D cube in two dimensional drawings. Studying this cube is a lesson in perspective drawing.

Overlapping the circles (so that the center of one is on the circumference of another) and making them opaque, yields this figure; the cube of three, composed of 27 spheres, 8 of which (2 cubed) are hidden, leaving 19 visible. This means that the cube of two is hidden with in the cube of three, just as the cube of 1 is hidden in the cube of 2. The cube of 4 conceals the cube of three.

Making the spheres transpart yields the figure known as "the flower of life", composed of vesicas. Note how you can see the "hidden" spheres, and how the center circle represents three different spheres; one at the front corner, one at the opposite corner and one in the middle of the cube.

The cube of 13 circles is an abbreviation of, or short-hand for, the cube with 27 spheres.
|
|
|
|
|
Réponse |
Message 6 de 23 de ce thème |
|
|
|
Whitney Houston ¿nueva víctima de los illuminati?Estamos tras la puerta del universo como bien decia Tesla, sobre el 3, 6, y el 9, hay que construir un conocimiento en base a estos conceptos, una buena forma y los Masones lo saben es a través de la geometria. http://es.wikipedia.org/wiki/Toro_(geometr%C3%ADa) Toro (geometría) Para otros usos de este término, véase Toro. En geometría, un toro es una superficie de revolución generada por una circunferencia que gira alrededor de una recta exterior coplanaria (en su plano y que no la corta). La palabra «toro» proviene del vocablo en latín torus, el cual en castellano significa «bocel» o «murecillo», que es una moldura redondeada de la basa, con forma de hogaza de pan.1 2  Si hacemos un corte longitudonal de Toro obtenemos la Vesica Piscis, como siempre los nombres no son elegidos por que si, Benicio del Toro, etc.
 |
Click para ampliar |
 Animación mostrando un toro siendo cortado por un plano, creando Círculos de Villarceau. Ver Vesica Piscis. Juan 6.33 Porque el pan de Dios es el que baja del cielo, y da vida al mundo.
 |
Click para ampliar |
 En cuanto a los cubos de los hipercubos, al juntarse el 9 y el 6 claramente chocan los ejes de los hipercubos, esto en definitiva es lo que produce el fuego y energia para el nuevo ciclo, puedes apreciar como en la forma octogonal el 6 y el 9 rotan sin problemas formando la estrella de 8 puntas, en el octogono mantienen la maxima distancia durante el ciclo, la llamada era dorada que viene despues del cataclismo, codigo de las manzanas doradas en el jardin de las hermanas Hesperides. Estrella binaria - Wikipedia, la enciclopedia libreSistema binario girando reciprocamente en espiral, se puede apreciar de donde sale la forma geometrica del 6 y el 9, al colapsar los espirales esto números se juntan dando lugar a una nuevo ciclo de tiempo.   La nebulosa del ojo del gato es un sistema trinario parecido pero con una estrella en el medio, se puede apreciar que dentro de la vesica piscis hay una estrella, otras 2 la orbitan, de allí parte la singularidad, el codigo Mon de la Moon en Ingles Luna, codigo Da Vincia de la Mona Lisa, etc. De alli como fractales nuestros siete dias, que son las siete vidas del gato, etc.
 |
Click para ampliar |
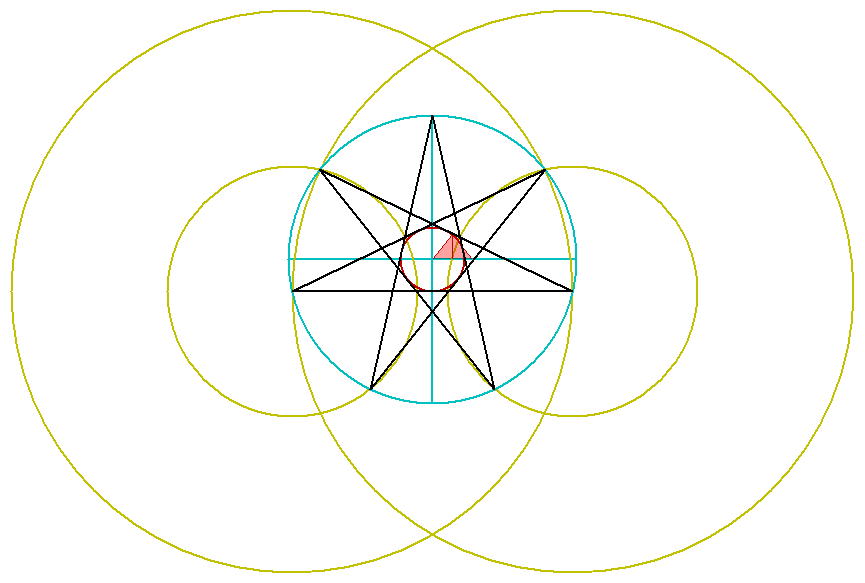
 Construccion el heptragrama
 |
Click para ampliar |
 |
Click para ampliar |
 En celeste tenemos enl heptagrama el cual coincide con el angulo de la gran piramide 360/7 =51.42 Podemos ver como la base el heptagrama es la gran piramide de Egipto, estos son los fractales del centro de la galaxia que producen nuestros siete dias, 28 dias del mes lunar, etc.Por lo tanto la gran piramide representa la singularidad geometrica, las bases representas los ciclos Alfa y Omega, cuando cambie nuestro espiral 6 a 9 y se inviertan la rotacion de los cubos, la precesion de los equinoccios llegara hasta la puerta de Leo, mas 90 grados llegamos a Omega, el mismo proceso a la inversa. En celeste tenemos enl heptagrama el cual coincide con el angulo de la gran piramide 360/7 =51.42 Podemos ver como la base el heptagrama es la gran piramide de Egipto, estos son los fractales del centro de la galaxia que producen nuestros siete dias, 28 dias del mes lunar, etc.Por lo tanto la gran piramide representa la singularidad geometrica, las bases representas los ciclos Alfa y Omega, cuando cambie nuestro espiral 6 a 9 y se inviertan la rotacion de los cubos, la precesion de los equinoccios llegara hasta la puerta de Leo, mas 90 grados llegamos a Omega, el mismo proceso a la inversa.Recordemos Omega - Libra - Lyra - las monedas de los imperios - Dios Apolo y su instrumento.
Última edición por IndigoMerovingio; 08-abr-2012 a las 17:18
|
|
|
|
|
Réponse |
Message 7 de 23 de ce thème |
|

from Mid-Atlantic Geomancy
If we want to talk with God/dess, experience has shown that it helps to be in the right environment. Spiritual seekers from Mayans through Christians, Native Americans, Egyptians and Hindus to the Neolithic builders of the stone rings in Britain and Ireland (and many more) found that by constructing their sacred places using certain geometrical ratios - just a small handful of them - they could more easily connect with their Maker.
Yes, it is possible to speak with our Creator anytime. However, sacred geometry makes this easier, and different ratios make different connections easier. The ratios have to do with different spiritual activities like healing, foretelling the future, long-distance communication, levitation and, most important, heightened ability to communicate with our Maker. These ratios help us to vibrate at the appropriate frequency to aid us in accomplishing the particular spiritual activity we have in mind.
Nearly every ancient archaeological site predating recorded history, from the Pyramids of Egypt and Mexico, to Stonehenge and beyond, employs mysterious mathematical alignments throughout their design.
These architectural formulas, rarely used today, are considered sacred and have also been found in the way they're arranged relation to each other and, most inexplicably, in the Monuments of Cydonia, and the Face on Mars.
When one looks at sacred enclosures globally, there is a group of five mathematical ratios that are found all over the world from Japan's pagodas to Mayan temples in the Yucatan, and from Stonehenge to the Great Pyramid. These ratios are:
-
Square Root of Two = 1.414...
-
Square Root of Three = 1.732...
-
Square Root of Five = 2.236...
-
Phi = 1.618...
Phi is the Golden Section of the Greeks. It was said to be the first section in which the One became many.
-
Pi = 3.1416...
Pi is found in any circle. If the diameter is 1, the circumference is 3.1416 (C = D).
These are all irrational numbers. Pi can be taken to 1500 decimal places with no discernable pattern to it (is that Chaos?). Let's take a closer look at each of these special numbers, and see how we can find them in the sacred geometry used by geomancers around the world. All five of these numbers gain their meaning only when beaten against the One. They are all ratios of x:1. The One is where it begins.
Pi - 3.1416 : 1 - the Circle
|
Pi (3.1416 : 1) is found in any circle. In sacred geometry, the circle represents the spiritual realms.
A circle, because of that transcendental number pi, cannot be described with the same degree of accuracy as the physical square.
The circle is yin.
It is a good shape to do all kinds of spiritual activities in. It is good for groups to work in circles. There are many examples of sacred spaces that are circular.
|
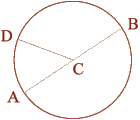
The Circle:
Radius (CD) = 1
Diameter (AB) = 2
Circumference = pi (3.1416) x Diameter
|
|

Ring of Brodgar, Mainland Orkney.
|
Most stone rings in the British isles are not actually circular.
Dr Alexander Thom proved this with his pioneering work in the sixties.
Some of the true circles are Merry Maidens in Cornwall, Stonehenge and the Ring of Brodgar.
|
Square Root of Two - 1.414 : 1 - the Square
|
In sacred geometry, the square represents the physical world.
It can be defined totally.
If its side is one, its perimeter is exactly four, and its area is one square - exactly.
The Square is yang.
|
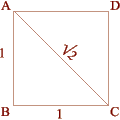
The Square Side (AB) = 1
Diagonal (AC) = Square Root of Two, 1.414
|
|
The Square Side (AB) = 1
Diagonal (AC) = Square Root of Two, 1.414
|
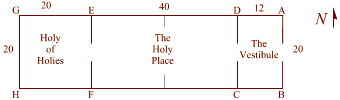
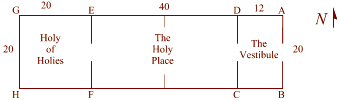
The square was found was in the Holy of Holies (the back room) of Solomon's Temple (G,H,F,E).
This was where the Hebrews kept the Ark of the Covenant and other most sacred treasures. (The dimensions here are taken from the first part of the Ezekiel Chapter 41.)
|
|
This is a view taken from inside the tower looking upward.

|

|
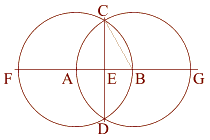
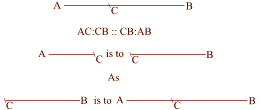
Square Root of Three - 1.732 : 1 - Vesica Pisces
The Vesica Pisces is created by two identical intersecting circles, the circumference of one intersecting the center of the other. The vulva-shaped space thus created is called the Vesica Pisces.
|
|
The Vesica Pisces:
Two Circles share a common radius (AB).
Radius AB = 1
The intersecting circles create a Vesica Pisces.
The minor axis of this Vesica Pisces (AB) = 1,
The major axis (CD) = the square root of three, 1.732
|
CB = AB
|
=
|
1 ..... Therefore:
|
|
a² + b²
|
=
|
c²
|
|
.5² + x²
|
=
|
1²
|
|
x²
|
=
|
.75
|
|
 2 2
|
=
|
 .75 .75
|
|
x
|
=
|
.8660 = CE
|
|
CE is 1/2 of the major axis CD
|
|
2 CE
|
=
|
CD
|
|
.8660 * 2
|
=
|
CD
|
|
CD
|
=
|
1.7320 = 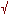 3 3
|
|
|
It covers one of the most powerful Holy Wells in Britain.
The Chalice Well has numerous examples of vesicas.
|

|
|

Gothic arch on the tower on the Glastonbury Tor. This site was a hermitage and retreat for early Christian monks
|

Gothic arch in Gallilee of Glastonbury Abbey. Note circular Romanesque arches behind in the Mary Chapel.
|
It is the sacred geometric shape of the Piscean Age.
|
Square Root of Five - 2.236 : 1 - the Double Square
|
The Double Square is found in some of the best known sacred spaces in the world, from the King's Chamber in the Great Pyramid and Solomon's Temple in the Bible to the interior of if(screen) { topPos=0; leftPos=0; } // in Vermont, USA.
The diagonal of a double square is to the shorter side as the square root of five is to one.
The square root of five = .618 + 1 + .618.
|
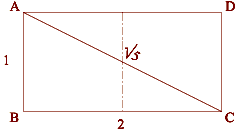
The Double Square:
Short Side = 1
Longer Side = 2
Diagonal = Square Root of Five, 2.236
|
|
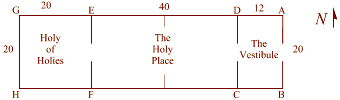
(ABCD) Double Square in Solomons Temple
|
if(screen) { topPos=0; leftPos=0; } // Open full page // // Open to size // var
The holy place (EFCD) is the place where good Jews who had been properly cleansed could go.
This space measures twenty cubits by forty cubits.
|
Another place where a double square is found is the Calendar II underground chamber site in central Vermont in the USA. It measures ten feet by twenty feet.
|

.
Calendar II, a drystone walled underground stone chamber in central Vermont, USA.
|

The interior of the chamber is 20 feet long by 10 feet wide , or 2 to 1. The chamber is oriented towards the Winter Solstice Sunrise.
|
Phi - 1.618:1 - Ø - the Phi Rectangle
|
The Golden Section, Phi, 1.618:
The shorter section on the right = 3
The longer section = 5
The shorter is to the longer
as the longer is to the whole
3:5 : : 5:8
|
In the Beginning was the One. In order to observe itself, it cut part of itself away to make 'Other'. This Golden Section is in beautiful proportion. As the subdividing continued away from the One, they continued in this phi ratio.
This can be used to go back to the One as well. It is in this sense that three is farther away from the One than two is.
Have you ever noticed that it is easier mathematically to go away from One than to go towards it? In other words, it is easier to add and multiply than it is to subtract and divide.
|
3:5 : : 5:8. This ratio indicates that it is part of this series: 1 . 2 . 3 . 5 . 8 . 13 . 21 . 34 . 55 . 89, and so on. This is called the Fibonacci Series. Start anywhere in the series, add the number below, and you get the next number (for example, 21 + 13 = 34). As one ascends up the series, any number in the series, when divided into the next one up, gets closer and closer to (but never hits exactly) 1.618, phi, the Golden Section.
|
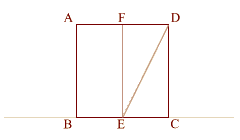
On a line create square
(ABCD) where AB = 1
|
|
|
Divide lines (AD) and (BC) in half
at (F) and (E). (BC) = 1, (EC) = .5
Double square (ECDF) is thus
created with a diameter of (ED).
|
|
|
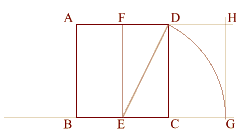
Using (ED) as a radius
swing arc from (D) downwards to 0
intersect the initial base line at (G).
Extend line (AFD), and create a
perpendicular to line (BECG) at (G)
so that it intersects line (AFD) at (H),
thus creating phi rectangle (ABGH).
|
|
|
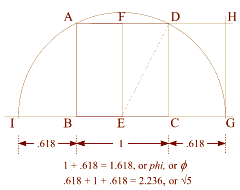
The formula that shows this is:
Phi = ( 1 + square root of 5 ) divided by 2
(BE) = 1/2
(ED) = 5/2
.5 + 1.118 = 1.618
|
|
Extend arc (DG) through (A) to (I).
Note the clear relationship between
phi and the square root of five.
|
|
|
|
Solomons Temple also contains phi. The Vestibule (DCBA) measures twelve cubits by twenty cubits. 12 to 20 can be reduced to 6 to 10 and further to 3 to 5.
Three and five are two numbers in the fibonacci series. 3/5 = 1.6, a close approximation to 1.618, or phi.
|
|
Calendar I was measured very carefully by the NEARA/ASD Earth Mysteries Group in the early 80's.
Three measurements of the length were taken and averaged.
The same was done with the width. Upon dividing the length by the width, the resultant ratio was 1.619 to 1. Phi (Ø) = 1.618 to 1.
|

|
|

|
The Parthenon is the Queen of Greek Temples, and personifies their interest in Sacred Geometry. If the height of the Parthenon is 1, its width is phi (Ø) 1.618, and its length is root of 5= 2.236. And 1.618 + .618 = 2.236.
These are the 5 sacred geometrical ratios - Pi, (2),(3),(5) and Phi. They are found in sacred spaces all over the world. Remember, sacred geometry is basically simple. You must do it with your hands, if you want to really know sacred geometry.
|
|
|
|
|
Réponse |
Message 8 de 23 de ce thème |
|
Helena (mitología)
De Wikipedia, la enciclopedia libre
Para otros usos de este término, véase Helena. Helena ( Ἑλένη en griego antiguo), a veces conocida como Helena de Troya o Helena de Esparta, es un personaje de la mitología griega; su leyenda es aludida por casi todos los mitógrafos clásicos. Era considerada hija de Zeus y pretendida por muchos héroes debido a su gran belleza. Fue seducida o raptada por Paris, príncipe de Troya, lo que dio origen a la Guerra de Troya.
Nacimiento
Zeus, metamorfoseado en un cisne, sedujo a Leda y yació con ella la misma noche que Tindáreo, esposo de Leda y rey de Esparta. Como consecuencia de ello, Leda puso dos huevos; de uno nacieron Helena y Pólux, ambos inmortales (considerados hijos de Zeus), y del otro Clitemnestra y Cástor, mortales (considerados hijos de Tindáreo). De todas maneras, se consideraba a Cástor y Pólux como gemelos y se los conocía como Dioscuros. Otras hermanas de Helena fueron Timandra y Filónoe.
Otra tradición decía que Helena había nacido de la unión de Némesis y Zeus, transformados respectivamente en oca y cisne. El huevo que puso Némesis fue encontrado por un pastor que lo entregó a Leda. Del huevo nació Helena y Leda la cuidó como si fuera su auténtica madre.[1]
[editar] Rapto de Helena por Teseo y Pirítoo

Teseo llevándose a Helena. Ánfora ática de figuras rojas. Siglo VI a. C. Staatliche Antikensammlungen, Múnich.
Helena fue famosa por su belleza desde que era una niña. Un día, mientras realizaba un sacrificio a la diosa Artemisa, fue sorprendida y raptada por el héroe ateniense Teseo en compañía de su amigo Pirítoo. Tras capturarla, echaron a suertes la doncella, correspondiéndole a Teseo. Pero cuando éste volvió a Atenas, el pueblo ateniense no permitió la entrada de la muchacha en la ciudad, motivo por el que Teseo la condujo a Afidna, junto a su madre Etra. A continuación, Teseo y Pirítoo decidieron marchar al Hades para raptar a Perséfone con la intención de convertirla en consorte de Pirítoo. Durante la estancia en el Hades de Teseo y Pirítoo, los Dioscuros rescataron a Helena. A su vez tomaron como prisioneras a la madre de Teseo y a la hermana de Pirítoo, que condujeron hasta Esparta para convertirlas en esclavas de Helena.[1] [2] [3]
Hay una tradición que mantiene que Helena y Teseo tuvieron como hija a Ifigenia, pero que, cuando Helena fue liberada por sus hermanos, ella decidió entregar a su hija a su hermana Clitemnestra, que ya estaba casada con Agamenón.[4] Pero la leyenda más extendida señalaba que Ifigenia era hija natural de Clitemnestra.
[editar] Boda con Menelao
Cuando Helena llegó a la edad de casarse, tuvo muchos pretendientes que acudieron desde todas las partes de Grecia, animados por la fama de su gran belleza y porque ella y su futuro esposo reinarían en Esparta. Tindáreo, temiendo provocar una guerra entre los pretendientes rechazados, siguió un consejo de Odiseo. A cambio, prometió a este su ayuda para conseguir a su sobrina Penélope como esposa.
El consejo de Odiseo consistía en arrancar a los pretendientes el juramento de acatar la decisión que se adoptase sobre quién sería el esposo de Helena y la obligación de acudir en auxilio del elegido si en algún momento su esposa le fuese disputada. Una vez realizado el juramento, Helena eligió como marido a Menelao, hermano de Agamenón, rey de Micenas (en otras versiones, de Argos), que, a su vez, se casó con su hermana Clitemnestra.
Menelao y Helena tuvieron una hija, Hermíone.
[editar] Rapto o seducción de Paris
La diosa Afrodita había prometido al príncipe troyano Paris el amor de Helena como premio por haber decidido a su favor en el concurso de belleza que la había enfrentado a Hera y Atenea.
Paris fue a Esparta, donde fue recibido hospitalariamente por Menelao y Helena. Sin embargo, durante su estancia, Menelao tuvo que viajar a Creta para asistir al funeral por la muerte de su abuelo materno, Catreo.
Afrodita provocó que Helena se enamorase de Paris, y los amantes huyeron juntos de Esparta con el tesoro de Helena mientras Menelao se encontraba aún en Creta. Se unieron por vez primera en una isla de localización incierta llamada Cránae. Hera les envió una tempestad y, tras pasar por Chipre y Fenicia, llegaron a Troya.[5] [6]
Otra versión señala que en realidad Helena no viajó con Paris a Troya sino que Zeus, Hera o Proteo formaron un espectro suyo, que fue lo que acompañó a Paris mientras la auténtica Helena fue trasladada a Egipto por Hermes. Se cree que la primera fuente de esta versión fue la palinodia compuesta por el poeta lírico Estesícoro, de la que quedan escasos fragmentos. Una leyenda añadía que el poeta había sido cegado por Helena (una vez que ésta había sido divinizada) a causa de que anteriormente había compuesto un primer poema que la trataba muy desfavorablemente. Cuando Estesícoro compuso su palinodia, se le devolvió la vista.[7] [8] [9] Un escolio atribuye a Estesícoro un comentario según el cual Afrodita hizo infieles a Helena y a sus hermanas Clitemnestra y Timandra para castigar a Tindáreo, que había olvidado ofrecer sacrificios a la diosa.[10]
Otra tradición narra que Paris raptó a Helena y la llevó consigo por la fuerza.
[editar] Guerra de Troya
Los mitógrafos discrepaban acerca de cómo fueron recibidos Helena y Paris cuando llegaron a Troya. Algunos decían que fueron mal recibidos por el pueblo, pero los hermanos de Paris y la reina Hécuba la recibieron favorablemente. Otros afirmaban que todos los troyanos se enamoraron de Helena e incluso el rey Príamo juró que nunca la dejaría marchar. Por su parte, la adivina Casandra vaticinó que Helena sería la ruina de la ciudad, pero no fue creída.[11] [12] [13]
Menelao, acompañado por una gran coalición de ejércitos comandados por los antiguos pretendientes de Helena y otros caudillos aqueos, zarpó hacia Troya en busca de su esposa.
Antes del inicio de la guerra, Menelao y Odiseo fueron como embajadores a Troya para reclamar a Helena y el tesoro que se había llevado con ella, pero los troyanos se negaron a devolverla y los hubieran matado a no ser por la intervención de Antenor, anciano consejero troyano, a su favor.[14] Por su parte, Partenio de Nicea señala en Sufrimientos de amor que los encargados de reclamar a Helena fueron Diomedes y Acamante.
Heródoto ofrece una versión diferente: los troyanos aseguraban que no tenían en su poder a Helena ni sus tesoros y que todo ello estaba en Egipto con su rey Proteo. Los griegos creyeron que los troyanos se burlaban de ellos, pero cuando conquistaron por fin Troya, Helena no apareció, y entonces sí creyeron a los troyanos y Menelao fue enviado a Egipto en busca de su esposa. Heródoto se adhería personalmente a esta versión, argumentando que si Helena hubiera estado en Troya habría sido devuelta a los griegos porque ni Príamo ni el resto de los troyanos habrían aceptado correr el riesgo de la guerra solo para complacer a Paris.[15]
Algunos autores antiguos relatan que, durante la guerra, Afrodita y Tetis concertaron un encuentro entre Helena y Aquiles.[16]
[editar] Helena en la Ilíada
Helena es un personaje importante de la Ilíada. Es estimada y respetada por el rey Príamo y por Héctor, mientras que los habitantes de Troya reconocen su belleza divina pero le atribuyen la causa de los males que padece su ciudad.[17] Presenta los principales caudillos aqueos desde la torre de la ciudad a su suegro, Príamo. Desde allí presencia el duelo singular entre su anterior esposo, Menelao, y el príncipe Paris.[18] Discute con Afrodita cuando ésta la incita a que vaya junto a Paris una vez que ha concluido el duelo pero luego, por miedo a las amenazas de la diosa, cede.[19] [20]
En la parte final del poema, Helena se lamenta por la muerte de su cuñado Héctor y señala que lleva ya veinte años en Troya.[21]
[editar] Helena en los hechos posteriores a los narrados en la Ilíada
Córito era un hijo que Paris había tenido con su anterior esposa: la ninfa Enone. Córito se enamoró de Helena y se decía que era un amor correspondido. Cuando Paris los descubrió, mató a Córito. Algunos mitógrafos, en cambio, señalaban que Córito era uno de los hijos de Helena y Paris.[22]
En el transcurso de la guerra, Paris murió y Helena fue obligada a contraer un nuevo matrimonio con Deífobo, otro de los hijos de Príamo. Por esta causa, otro hijo de Príamo, Héleno, que estaba enamorado de Helena, abandonó Troya. Como, igual que su hermana Casandra, tenía el don de la adivinación y Calcas, adivino de los griegos, sabía que conocía los oráculos que protegían la ciudad, Odiseo lo capturó, lo llevó al campamento y lo obligaron a revelar esos oráculos.[23]
Helena reconoció a Odiseo cuando éste penetró en Troya como espía disfrazado de mendigo, pero no lo denunció. Los aqueos, para entrar en Troya, construyeron un caballo de madera y un puñado de guerreros destacados se escondieron en su interior. Los troyanos, ignorantes del contenido del caballo, lo introdujeron en su ciudad. Antes de que los guerreros salieran del caballo, la astuta Helena, conocedora del plan de los aqueos, dio varias vueltas a su alrededor acompañada de Deífobo, imitando las voces de las esposas de los guerreros griegos. Los aqueos estuvieron a punto de responder desde dentro del caballo y delatarse.[24]
En algunas versiones, Helena fue la que agitó una antorcha desde su habitación durante la noche, que era la señal esperada por los aqueos: la de que las puertas de Troya iban a ser abiertas por los hombres que habían salido del caballo.[25]
La guerra terminó con el triunfo de la coalición aquea. Menelao mató a Deífobo y a punto estuvo también de matar a Helena, pero quedó deslumbrado y enamorado de nuevo por su hermosura y la perdonó. Algunos autores antiguos cuentan que fue la propia Helena la que mató a Deífobo y que Menelao perdonó a Helena cuando vio sus pechos desnudos.[26] [27] [28] Tras un viaje de retorno accidentado en el que tuvieron que pasar una larga temporada en Egipto, ambos regresaron a Esparta. En el Ática existe una isla a la que se llamaba Isla de Helena, porque se creía que en ella había desembarcado durante su retorno a la Hélade.[29] Tras este retorno, Helena y Menelao fueron padres de Nicóstrato, según algunos autores.
[editar] Helena en la Odisea
Helena aparece como personaje en la Odisea, principalmente en el Canto IV. En el viaje realizado en busca de noticias de su padre Odiseo, Telémaco llega a Esparta, donde se entrevista con Helena y Menelao, que han vuelto a reinar allí.
Homero afirma categóricamente que Helena tuvo como única descendiente a su hija Hermíone.[30]
Helena ejerce de anfitriona junto con su esposo y recuerda algunos de los sucesos ocurridos en la guerra de Troya.
|
|
|
 Premier
Premier
 Précédent
2 a 8 de 23
Suivant
Précédent
2 a 8 de 23
Suivant Dernier
Dernier
|

