Un poco de Historia
El cálculo de la razón de oro se remonta a la Antigua Grecia que era el epicentro de la cultura del mundo antiguo con diferencia.
No se sabe como se le ocurrió medir a Pitágoras esa razón, Pitágoras fue además el descubridor de la razón de la suma de los cuadrados de los catetos y el cuadrado de la hipotenusa en triángulos cuadrados, sea como fuera en ese contexto tan especial como la Antigua Grecia que fue una de las épocas más asombrosas de la historia mundial se calculo la razón áurea, siendo Pitágoras el que la calculo.
Pitágoras tenía mucho poder en esa Grecia donde apareció una luz intensa que que cubría todos los campos tanto de artes de letras como de matemáticas.
En las Universidades actuales tanto el cálculo del número áureo como la relación entre la hipotenusa y los catetos de un triángulo cuadrado puede considerarse como matemáticas para niños.
Si alguien de letras quiere profundizar en las Matemáticas, Física o Química debe estudiar Historia de la ciencia, que además de darle una visión del contexto temporal de los descubrimientos científicos le dará también una visión de la importancia de los descubrimientos.
No es recomendable para un neófito en Matemáticas o Física profundizar en la parte teórica y práctica de estas materias ya que con lleva mucho trabajoy varios años conseguir defenderse en este ámbito.
Cuando Kepler dijo que las dos relaciones anteriores eran una joya preciosa a mi me sorprendió un poco.
El primer descubrimiento de Pitágoras no está mal si la situamos en el ámbito histórico de la antigua Grecia aunque ahora la consideraríamos matemáticas de niños, sin embargo lo de denominar el número áureo como joya preciosa despertó mi curiosidad hay que tener en cuenta que los otros dos números irracionales importantes pi como el número e tienen una importancia vital en física, tanto en mecánica como electromagnetismo, sin embargo hasta donde yo conozco el número phi no tienen ninguna aplicación en física ni matemáticas.
Tanto su leyenda de proporción divina como de número de la belleza no tienen ningún fundamento, lo mismo que su uso en economía, proporciones de estatuas o biología.
Es un auténtico misterio porqué Kepler se interesó tanto en él y fue el que primero profundizo en el tema de su cálculo ya que podemos situar claramente a Kepler en el top diez de los físicos sin equivocarnos en absoluto y seguramente algunos entre los que me incluyo lo situaríamos en el top cinco junto a Newton Gauss y Einstein.
El número áureo en relatividad
Ahora vamos a trabajar con el efecto Doppler.
A principios del siglo XVIII se inició el camino hacia la relatividad con Huygens o sea que todo era relativo según la velocidad propia de cada cuerpo.
Doppler marcó claramente el camino a la teoría de la relatividad de Einstein en el siglo XIX con el efecto Doppler
Doppler descubrió una fórmula que media la frecuencia con la que percibimos un sonido dependiendo de la velocidad relativa que tengamos con la fuente del sonido, dicho de otra manera dadas dos personas es imposible que oigan la misma frecuencia de un sonido, aunque a veces la diferencia es tan mínima que podemos considerar que dos personas pueden oír prácticamente con la misma frecuencia un sonido.
El asunto es que si consideramos una velocidad relativa igual al número áureo en la formula del efecto Doppler y hacemos los cálculos en dicha fórmula pude encontrar cinco relaciones matemáticas usando los logaritmos, siempre he creído que dos podía ser casualidad, pero con cinco ya no se podía hablar de tanta casualidad.
Quien quiera estudiar esas mediciones le recomiendo que lea el efecto Dopler en el cerebro humano del mismo autor que este libro.
Pero al intentarlo con las transformaciones de lorentz que explican matemáticamente la teoría de la relatividad de Einstein, ya me convencí absolutamente que había demasiadas casualidades entre la teoría de la relatividad y el número áureo si considerábamos la fracción la velocidad de un objeto respecto a la velocidad de la luz igual a 0.681 o sea el inverso del número áureo.
Metiendo estas relaciones en ambas fórmulas y aplicando logaritmos encontré hasta diez mediciones que solían dar el número áureo y en dos ocasiones el número e y en otra el número pi.
No las voy a poner aquí ya que no encontré una sucesión lógica entre ellas aunque fuera difícil de catalogar las diez mediciones como casualidades.
Si consideramos la ecuación:
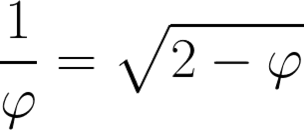
Se me ocurrió esta expresión con las transformaciones de Lorents donde en el numerador igualaba todo a uno y en el denominador en vez de poner (1-v^2/c^2)^1/2 ponía (2-phi)^1/2 igualándolo todo al inverso de phi o sea del número aúreo
La verdad es que es un poco complicado decir como la deduje, yo no la encontré por ninguna parte. Sólo decir que me inspiré en las transformaciones de Lorentz y los polinomios que vamos a ver más adelante tienen soluciones comunes por lo menos dos a dos como mínimo y a veces más en los puntos:
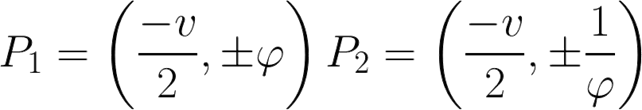
Ahora la voy a generalizar para todos los números reales y quedaría como:
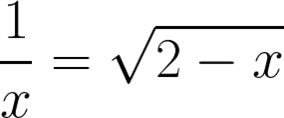
Ahora quito la raíz y elevo 1/x al cuadrado.
Esta operación es a todas luces ilegal en matemáticas pero funcionó y me hizo descubrir el primero polinomio de esta base que tiene una raíz que el es número áureo, su inverso y la unidad.
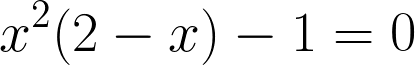
De aquí sale un polinomio que es:
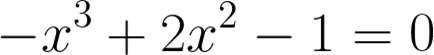
Esta ecuación de tercer grado tiene tres raíces reales que son:
X1 = -0.6180339887
X2 = 1.6180339887
X3 = 1.00000000
O SEA LA PRIMERA ES LA INVERSA DEL NÚMERO AÚREO CON SIGNO NEGATIVO
LA SEGUNDA ES EL NÚMERO AÚREO
LA TERCERA ES LA UNIDAD
El siguiente polinomio también tiene tres raíces reales iguales que el anterior sólo que el número áureo y su inverso están cambiados de signo
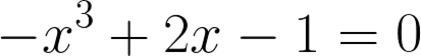
X1 = 0.6180339887
X2 = -1.6180339887
X3 = 1.00000000
O SEA LA PRIMERA ES LA INVERSA DEL NÚMERO AÚREO
LA SEGUNDA ES EL NÚMERO AÚREO CON SIGNO NEGATIVO
LA TERCERA ES LA UNIDAD
Por último el polinomio siguiente tiene también tres raíces reales:
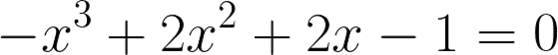
-1.000000000 =x1:
2.618033989 =x2:
0.381966011 =x3:
O SEA LA PRIMERA ES LA UNIDAD CON SIGNO NEGATIVO
LA SEGUNDA ES EL CUADRADO DEL NÚMERO AÚREO
LA TERCERA ES LA RAZON DEL SEGMENTO PEQUEÑO DE UN SEGMENTO TOTAL DE LONGITUD LA UNIDAD
Los tres polinomios tienen una única solución en común que es -1 en x=0
Pero vayamos más allí, si hacemos un sistema de ecuaciones con las tres ecuaciones anteriores y la archiconocida ecuación:
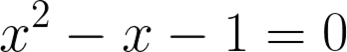
Tenemos que el determinante de la matriz de cuatro x cuatro compuesta con las cuatro ecuaciones tiene determinante = 4
Obviamente la matriz tiene rango 4 que es una base de dimensión 4
La solución del sistema de estas cuatro ecuaciones es también x=-1
Esto empieza a ser sorprendente por lo que me llevó a pensar que se puede encontrar cualquier polinomio de cualquier grado que satisfagan el número áureo y además que unidos a estos polinomios sea una base de cualquier dimensión.
Probé con un polinomio de cuarto grado que es el siguiente:
Que tiene 4 raíces reales
X1 = 0.6180339887
X2 = -1.6180339887
X3 = 1.00000000
X4 = -1.00000000
O SEA LA PRIMERA ES LA INVERSA DEL NÚMERO AÚREO
LA SEGUNDA ES EL NÚMERO AÚREO CON SIGNO NEGATIVO
LA TERCERA ES LA UNIDAD
LA CUARTA ES LA UNIDAD CON SIGNO NEGATIVO
Y también satisface la raíz -1 en x=0
Si hallamos el determinante de este sistema de 5 ecuaciones:
|
det A =
-1
|
-1
|
2
|
1
|
-1
|
|
0
|
-1
|
2
|
2
|
-1
|
|
0
|
-1
|
2
|
0
|
-1
|
|
0
|
-1
|
0
|
2
|
-1
|
|
0
|
0
|
1
|
-1
|
-1
|
|
|
|
Tenemos sorprendentemente que el determinante vuelve a ser 4
Resumiendo podemos subir un grado el polinomio y ajustando el valor del valor de x en un nuevo polinomio de grado x^n tendremos que nuevamente satisface el número áureo su inverso y su cuadrado, teniendo n raíces reales. Y además forman una base.
Vamos con un polinomio de grado 5
Las raíces del polinomio -x5-x4+2x3+2x2-1 son:
x1=0.61803
x2=1.32472
x3=-1.61803
x4=-0.66236+0.56228*i
x5=-0.66236-0.56228*i
Resultados
Las raices del polinomio -x6-x5+2x4+2x3+3x2-1 son:
x1=0.48403
x2=-0.61803
x3=1.61803
x4=-1.89718
x5=-0.29342+1.00144*i
x6=-0.29342-1.00144*i
Ahora viene algo importante la multiplicación de cualquiera de estos polinomios nos da otro polinomio que también tiene como raíz el número áureo y su inverso
Por ejemplo: (-x^4-x^3+2*x^2+x-1)*(-x^5-x^4+2*x^3+2*x^2-1) = x^9 + 2x^8 - 3x^7 - 7x^6 + 2x^5 + 8x^4 + x^3 - 4x^2 - x + 1
cuyas raices son:
Resultados
Las raices del polinomio (x9+2x8-3x7-7x6+2x5+8x4+x3-4x2-x+1) son:
x1=1
x2=-1
x3=0.61803
x4=0.61803
x5=1.32472
x6=-1.61803
x7=-1.61803
x8=-0.66236+0.56228*i
x9=-0.66236-0.56228*i
Con el número áureo y su inverso con dos raíces reales cada uno y otras dos para la unidad.
Este último polinomio multiplicado por otro de nuestra base nos da otro polinomio:
(x9+2*x8-3*x7-7*x6+2*x5+8*x4+x3-4*x2-x+1)(-x^6-x^5+2*x^4+2*x^3+3*x^2-1)=
-12x^7 - 13x^6 + 23x^5 + 26x^4 + 38x^3 + 3x^2 - 12x - 1
Cuyas raices son:��Resultados
Las raices del polinomio -2x7-13x6+23x5+26x4+38x3+3x2-12x-1 son:
x1=-112
x2=0.48403
x3=-0.61803
x4=1.61803
x5=-1.89718
x6=-0.29342+1.00144*i
x7=-0.29342-1.00144*i
Donde aparecen otra vez soluciones del número áureo y su inverso.
Una vez que ya sabemos conseguir polinomios cuyas soluciones son el número áureo a partir de nuestra base voy a pasar a otro sorprendente resultado.
Pero ahora vamos quizás con la parte más importante y es que resuelven estos polinomios.
Si introducimos estos polinomios en las transformaciones de Lorentz
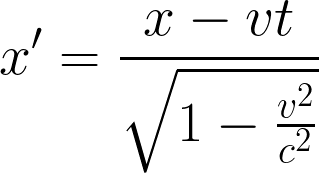
como una trayectoria o sea x = P(x)
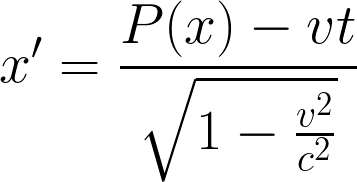
y consideramos una velocidad por el tiempo constante y de valor vt = 2 para todos ellos y tomándolos de tres en tres.
Los tres tienen al menos una solución común en:
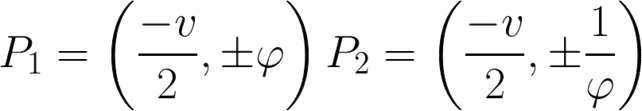
y además dos de ellos tienen una solución en cualquiera de los cuatro puntos anteriores.
(v) Tiene que ser constante en las tres ecuaciones y (c) puede tomar cualquier valor común a las tres ecuaciones.
En el siguiente gráfico vemos que tres polinomios de nuestra familia de grados 9,10 y 13 tienen una solución común en P(0.618033989,-2)
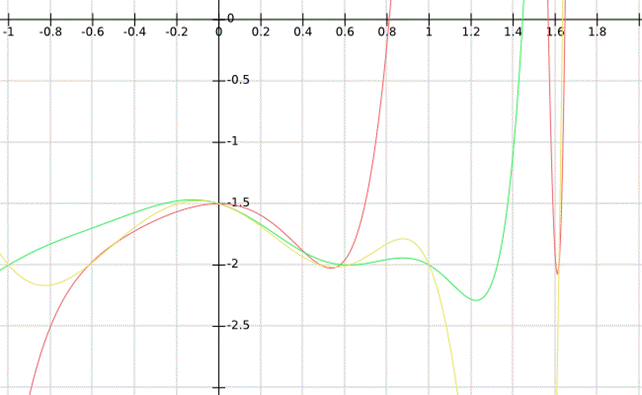
Autor:
Pedro Hugo García Peláez
Reservados todos los derechos. No se permite la reproducción total o parcial de esta obra, ni su incorporación a un sistema informático, ni su transmisión en cualquier forma o por cualquier medio (electrónico, mecánico, fotocopia, grabación u otros) sin autorización previa y por escrito de los titulares del copyright. La infracción de dichos derechos puede constituir un delito contra la propiedad intelectual.
© Pedro Hugo García Peláez, 2016

