Tema anterior
Primer 
Phi (Φ) was described by Johannes Kepler as one of the “two great treasures of geometry.” (The other is the Theorem of Pythagoras.)
Phi appears in many basic geometric constructions.
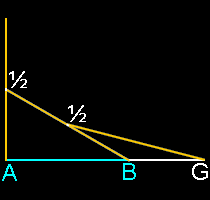
3 lines:
Take 3 equal lines. Lay the 2nd line against the midpoint of the 1st. Lay the 3rd line against the midpoint of the 2nd. The ratio of AG to AB is Phi, the Golden Ratio. (Contributed by Jo Niemeyer)
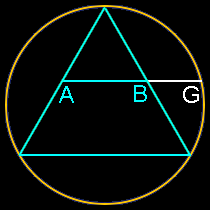
3 sides: Triangle
Insert an equilateral triangle inside a circle, add a line at the midpoint of the two sides and extend that line to the circle. The ratio of AG to AB is Phi.
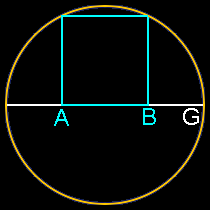
4 sides: Square
Insert a square inside a semi-circle. The ratio of AG to AB is Phi.
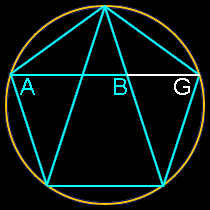
5 sides: Pentagon
Insert a pentagon inside a circle. Connect three of the five points to cut one line into three sections. The ratio of AG to AB is Phi.
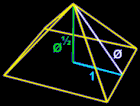
When the basic phi relationships are used to create a right triangle, it forms the dimensions of the great pyramids of Egypt, with the geometry shown below creating an angle of 51.83 degrees, the cosine of which is phi, or 0.618.
A ruler and compass can be used to construct the “golden rectangle,” as shown by the animations below, which was used by the Greeks in the Parthenon. (See also the Orthogons page.)
Phi also defines other dimensions of a pentagon.
There are also a number of geometric constructions using a circle which produce phi relationships, as shown on the Geometric Construction of Phi in Circles page.
Phi can be related to Pi through trigonometric functions
Note: Above formulas expressed in radians, not degrees
Phi appears in 3D geometric solids
| Take three golden rectangles and assemble them at 90 degree angles to get a 3D shape with 12 corners: |
Click on the shape below and the print the page to do it yourself: |
|||||||||||||||
|
|
|
|||||||||||||||
This is the basis for two geometric solids |
||||||||||||||||
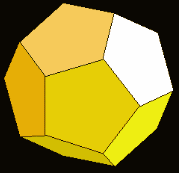
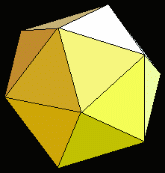
| The 12 corners become the 12 centers of each of the 12 pentagons that form the faces of a dodecahedron. | The 12 corners can also become the 12 points of each of the 20 triangles that form the faces of a icosahedron. | |||||||||||||||
Dodecahedron
|
Icosahedron
|
|||||||||||||||
|
||||||||||||||||
Some interesting aspects of dodecahedrons and icosahedrons:
A dodecahedron with sides of length 1 embeds a cube with sides of length is Phi.
An icosahedron with sides of length 1, the dual dodecahedron has sides with length 1/Phi. In other words, the dual of the dodecahedron with side of length 1 is an icosahedron with sides of length Phi.
Learn more about phi and geometry on the Penrose Tiling and Quasi-crystals pages.
