|
|
rawing the Hypercube # 1 - YouTube
www.youtube.com/watch?v=ccws454YiVM
14/08/2008 - Subido por ProfessorElvisZap
Professor Zap shows how to draw a hyper cube in real time.
www.youtube.com/watch?v=NE9ZFDJ4Phk
06/12/2009 - Subido por brethilaki
Video Responses · Thumbnail How to Draw a Hypercube (Tesseract) with 8 Squares by BRyanS72 2,662 ...
www.metacafe.com/.../discover_the_4d_the_impossibl...
03/06/2007
I am drawing there the HYPERCUBE; a cube that is impossible to imagine in a 3D world. Th. Watch Video ...
|
|
|
|
|
HIPERCUBO EN 4 DIMENSIONES 16 PUNTOS
HIPERCUBO EN 5 DIMENSIONES 32 PUNTOS
6 DIMENSIONES 64 PUNTOS
|
|
|
|
|
HIPERCUBO EN FORMA FISICA
|
|
|
|
|
Hypercube Representations-2

The previous page considered ways to present magic squares and cubes (2-D and 3-D objects).
This page considers magic tesseracts (4-dimensional objects).
Historical representations Hendricks modern form The first tesseract

Historical representations
- Magic squares are 2-dimensional objects consisting of 4 edges that meet 4 corners at right angles. They are easy to illustrate on a 2-dimensional surface.
- Magic cubes are 3-dimensional objects consisting of 12 edges meeting 8 corners at right angles . They are easy to see in 3-dimensional space, but can be illustrated on a surface (2-D) only by introducing distortion.
- A magic tesseract is a 4-dimensional object consisting of 32 edges meeting 16 corners at right angles. A model of a tesseract could be built in 3-dimensional space, but only by introducing distortion (the corners would not be right angles). A drawing of a tesseract obviously requires still more distortion!
| In trying to visualize a tesseract, 2 types of drawings have been used for many years. This one shows a small cube 'suspended' inside a large cube and 'supported' by six distorted cubes.
This is the best illustration to show how each tesseract is 'bounded' by 8 cubes (6 of them are distorted).
|

|
| This drawing illustrates the second visualization (the figure to the right).
The drawing as a whole attempts to show how a hypercube may be 'dragged' through the dimensions to produce a hypercube illustration for each. i.e here we go from 0-dimension to 1, 2, 3, and finally arrive at the forth dimension.
The numbers help to identify the corners. As an 'extra', I have arranged the numbers so that each square (and rhomboid) is perimeter magic. Remember that in these two cases, the rhomboids are actually distorted squares!
In both examples, the drawing is obviously not suitable to display the numbers in the magic tesseract. Even for order-3, the lowest, there are 81 numbers to display.
|

|

Hendricks modern form
In 1962, John R. Hendricks published a new method of drawing the magic tesseract [1][2]. He did it in grand style by describing a 6-dimension magic hypercube of order-3. This hypercube used the numbers from 1 to 729 (729 = 36) and required 9 order-3 dimension 4 (tesseract) figures to display (a 6-D figure was just too complicated to comprehend). Each tesseract sums on its own in 4 ways. The fifth direction is found by jumping from tesseract to tesseract horizontally, and the sixth direction by jumping vertically. The resulting normal 6-dimensional magic hypercube sums to 1095 in at least 1490 ways (6m5 + 32).
He also showed a 5-dimension order-3 magic hypercube. It required three order 3 tesseract diagrams. See this hypercube here.
 
He introduced the subject with figures 1, 2, and 3; showing an order 3 magic square, magic cube, and magic tesseract. Notice that none of the three magic figures are normalized. He came up with that idea (for cubes and tesseracts) at a later date, when he realized that a system was required for listing solutions in order. This tesseract is an aspect of index # 5.
The magic square has traditionally been illustrated with each number occupying a 2-dimensional 'cell', not as intersections of a 'grid' as suggested in Figure 1 (above). The magic cube was also shown that way at the start, but now is normally shown with the numbers placed at grid intersections.
This tesseract diagram is now the one in universal use for displaying small orders of 4-dimension magic hypercubes.
For the larger orders, a simple text listing is still the most practical.
This is one way of listing the above tesseract
09 76 38 64 35 24 50 12 61
46 17 60 05 75 43 72 31 20
68 30 25 54 13 56 01 80 42
74 45 04 33 19 71 16 59 48
15 55 53 79 41 03 29 27 67
34 23 66 11 63 49 78 37 08
40 02 81 26 69 27 57 52 14
62 51 10 39 07 77 22 65 36
21 70 32 58 47 18 44 06 73
The purpose of this page is to show methods of illustrating a magic tesseract. Other pages on this site will discuss features and characteristics of the magic tesseract, and the relationships between this 4-d magic figure and it's 2-D and 3-D cousins.)
[1]John R. Hendricks, The Five and Six Dimensional Magic Hypercubes of Order 3, Canadian Mathematical Bulletin, vol. 5, no. 2, 1962, pp 171-189
[2]John R. Hendricks, Magic Squares to Tesseracts by Computer, Self-published 1998, 0-9684700-0-9 the preface contains some history of this discovery

The first magic tesseract?
In 1905, Dr. C. Planck published a paper [1] [2] for private circulation. Called The Theory of Paths Nasik, It dealt with perfect magic squares and cubes.
Dr. A. H. Frost defined the term Nasik in 1878 [3] as requiring that all paths sum correctly. He stated that the smallest order Nasik magic square is order-4 ( we call it pandiagonal), and the smallest order Nasik magic cube is order-8.
In explaining his theory, Dr. Planck constructed the order-9 pandiagonal magic square shown in 2. He then took the nine order-3 sub-squares and arranged them as shown in illustration 1. He called this a 'crude-magic octahedron.
 1 1
|
 2 2
as an order-9 pandiagonal magic square |
 3 3
another aspect of the same magic tesseract |
hh-1 (to the right) is the modern method of displaying the 4-dimension magic hypercube.
All lines parallel to the edges, and also the 8 quadragonals, sum correctly to the constant 123.
I quote from his paper
|
...we shall obtain the three cubes of order 3 shown in figure 11, which form a perfect crude-magic octahedroid of order 3. These three cubes are sections of the four-fold made by three parallel equidistant spaces, laid out in perspective in one space of three dimensions.
|
Some points
-
The 3x3 squares in figure 11 are not magic, nor are the 3x3x3 cubes that may be formed from them. This is because the diagonals and triagonals do not sum correctly. This is not a requirement of a magic tesseract. The eight Quadragonals of the tesseract (such as 47+41+35) is a requirement and does sum correctly.
-
Figure 11a is shown in green in the modern drawing with the other two cubes parallel to it. The three cubes of fig. 12 are parallel to the front of the drawing.
-
This tesseract is 1 of 384 aspects of the 58 basic magic tesseracts of order 3. It is a non-normalized aspect of index number 57 (of the 58).
-
Usually, to make the drawing simpler, only the outline lines are shown (see previous section).
-
hh-2 is another aspect of the same 'octahedroid'. Do you see where Planck,s cubes fit in this drawing?
Perfect?
Planck's paper expanded on Frost original definition of Nasik, applying it to hypercubes where all lines sum correctly i.e. perfect hypercubes.
I must emphasize, though, that this tesseract is not perfect (and his paper did not suggest it was). Like all order-3 magic hypercubes, it is classed as a simple order-3 magic hypercube..
The smallest perfect magic tesseract possible is order-16. John Hendricks constructed the first one in 1999, and Clifford Pickover confirmed that it summed correctly to 524,296 in the required 163,840 ways (straight line paths only). [4] [5]
|

hh-1 Modern day presentation of planck's 'octahedroid'
|
|

hh-2 This is another aspect of the same tesseract
|
[1] Dr. C. Planck, The Theory of Paths Nasik, self-published in Haywards Heath, (England) in November 1905. 18 pages self-cover.
[2] W. S. Andrews, Magic Squares and Cubes,2nd Edition, Open Court, 1917, pages 363-375 written by C. Planck.
This book republished by Dover Publ. in 1960. The above fig. 10 and 11 (from the 1905 paper appear in Andrews as fig. 687 and 688.
[3] A.H. Frost, On the General Properties of Nasik Cubes, Quarterly Journal of Mathematics, 15, 1878, pp 34-49.
[4] John R. Hendricks, Magic Squares to Tesseracts by Computer, Self-published 1998, 0-9684700-0-9 pp 126-127 (and private correspondence)
[5] Clifford A. Pickover, The Zen of Magic Squares, Circles, and Stars, Princeton University Press, 2002, 0-691-07041-5, page 121.
|
|
|
|
|
How to Draw a 4D Hypercube (My Way)
"In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube."
A Tesseract is a Four Dimensional Hypercube
If you're drawing a square on a flat sheet of paper, how many straight lines does it take? Four. If you're drawing a cube, how many squares (sides) does that take? Six. So if you're drawing a tesseract, how many cubes does that take? Eight!
In this hub, I'm going to show you how to draw your very own tesseract! The lengths of the lines and the angles won't be exact, however, because I'm not using a ruler for this tutorial.
First: How to Draw an Ordinary Cube
Step 1: Draw two lines of equal length, attempting to keep them an equal space apart, at slightly different heights.
Step 2: Connect the two lines as shown, creating what looks like a smooshed square, or a fat diamond that fell over.
Step 3: Draw four parallel lines stemming from each of the shape's four corners.
Step 4: Connect the ends of the two top lines, the ends of the two bottom lines, and then connect each bottom line with the line above.
Visual instructions for drawing the tesseract follow below:
Step 6
Step 7
Step 8
Step 9
Step 10
Step 11
Step 12
Step 13
Step 14
Step 15
Step 16
Step 17
Step 18
Step 19
Step 20
And there you have it! A complete two dimensionally rendered tesseract, and only twenty-three steps later. I hope you enjoyed my little tutorial!
If you're interested to learn more about four dimensional geometry, try getting your hands on a copy of Geometry, Relativity, and the Fourth Dimension by Rudolf v. B. Rucker, published in 1977.
|
|
|
|
|
|
I’ve decided to write this post in order to try to give an answer to Eggshell Robotic question “Tesseract / Hypercube – Mechanical Possible?“… The main reason to make a post on my blog rather then making a comment on Eggshell Robotic’s post is mainly the fact that I wrote a lot… and I use images and links… so here it is :
A hypercube is basically 8 cubes organized using the same logic as we use to build a square (2 dimensions) with strokes (1 dimension), and to build a cube (3 dimensions) with squares (2 dimensions)… We take the first cube, join its 6 faces with one face of 6 other cubes… then we go to the 4th dimension by joining all faces that are next to each other… The 8th cube is used to close the hypervolume…

It might be easier to explain it comparing to the cube construction… We have 6 squares (2D) we take one to use as center. We join 4 other squares around the one in the center… (still in 2D)… Now we rotate the 4 new squares to the upper dimension in order to link theme (now we are in 3D) but the cube is not closed, therefore we have a 6th square to close the missing face of the cube… Here is a site showing part of the process.
http://beart.wordpress.com/2008/02/27/hypercube-construction/ |
|
|
|
|
|
Hypercubes
The most famous example of a higher dimensional object is the hypercube. Broadly speaking, the hypercube is to the cube as the cube is to the square. But, what does this mean? What can we determine about the geometrical properties of the hypercube?
The best way to grasp a picture of the hypercube is to work up to it dimension by dimension. We can start in zero dimensions and proceed onwards to produce a whole family of cubes. A point does not have any extension. It is the unique zero dimensional object. If we allow our point to sweep out a length of one unit, say along the x axis, we can produce a line segment. Next we can allow the line segment to sweep out a distance of one unit in a perpendicular direction, say one unit along the y axis. The figure that we will produce is a square. Next, our square can sweep out a distance of one unit in a direction perpendicular to the first two directions, say the direction along the z axis. The result will be a unit cube.
What happens next? We now seem to have run out of perpendicular directions in which we can continue this procedure. However, we can imagine that there are further perpendicular directions and envisage abstract higher dimensional space. There is no reason why we should restrict ourselves to the three dimensions of physical space; as long as we reason clearly and consistently, we can deduce the mathematical properties of higher dimensional objects, even if they cannot be physically realised in our three dimensional universe. We can simply declare that we are now working in four dimensional space and see where our exploration leads us. If we find ourselves in an interesting place, then that will be sufficient reward for our journey. Often the research of pure mathematicians is guided by the search for interesting abstract scenery rather than a quest for scientific utility. In our abstract four-dimensional space, there will be a fourth axis that is perpendicular to our other three axes. We can label this axis the w axis. Measuring the distance parallel to each of the four axes gives us four coordinates that will specify the position of any point within our four dimensional space.
With a fourth perpendicular direction that we might label the w axis, we can now take the cube and sweep it one unit along this direction. The object that we will generate is the four dimensional equivalent of the cube. It is the object of our dreams, our hypercube. So what does it look like? Is there any way that we can visualize it?
Our sections through a cube formed a sequence of squares. And similarly, our sections through the hypercube form a sequence of cubes. [We can imagine going down to two and one dimension to see how the analogy works in the case of the two-dimensional cube, which we usually call a square and the one-dimensional cube, which we usually call a line segment. (Our sequence of sections of a square are a sequence of line segments. Our sequence of sections of a line segment is a sequence of points.)]
What else can we infer from this description of a hypercube? If we draw the hypercube with an exaggerated perspective it will help us to understand the analogy with a cube. First we can draw a transparent cube face-on, so that we can see the back face within the front face and with edges connecting the corners of the front face to the corners of the back face. We can make a similar drawing of a transparent hypercube. If we position the hypercube in the same orientation as in our previous discussion, in our perspective drawing we will see a large cube, with a smaller cube within. Each of the corners of the outer cube are connected by edges to the corners of the inner cube. What we are looking at is the front cube (the outer cube) with the back cube, which is further away in four-dimensional space, appearing within it because its size appears diminished with distance. This is completely analogous to seeing the back face of the transparent cube within its front face.
|
|
| |
| |
 |
|
| |
| |
In the projection shown above, the front and back squares of the cube both look square, but the other four square faces of the cube do not look square. Similarly, in the projection of the hypercube, the front and back cubes of the hypercube both look cubical, but the projection has distorted the shapes of the other six cubes that form the hypercube. However, there are more symmetrical ways to project a hypercube down to two dimensions, in which the distortion is shared equally between all eight cubes. Such a projection is shown below. It gives a better feel for the structure of the hypercube. The outlines of each of the eight cubes can be picked out in this projection.
|
|
| |
| |
 |
|
| |
|
 |
| |
| |
| |
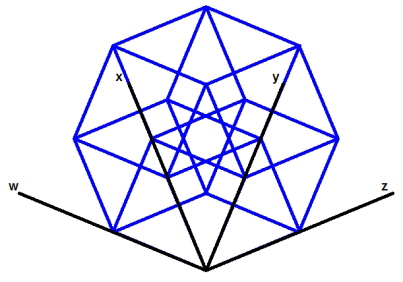
In the illustration shown above right, the axes have been given arbitrary labels: 'w', 'x', 'y' and 'z'. In four-dimensional space these would be the four mutually perpendicular axes. In this projection down to two dimensions, the 'w' and 'y' axes remain perpendicular and the 'x' and 'z' axes remain perpendicular, but the angle between the 'w' axis and the 'x' axis is now 45°.
|
|
| |
| |
 |
|
 |
|
| |
| |
On the left above, the twelve edges of one of the 8 cubic cells of the hypercube have been coloured red. The edges and faces of this cube are aligned with the 'w', 'x' and 'z' axes. In four-dimensional space, this cube is perpendicular to the 'y' axis. On the right, the edges of the opposite cubic cell have been coloured magenta. If we were looking along the 'y' axis, these would correspond to the front and back cube of the hypercube. Note that each corner of one cube is connected to a corner of the opposite cube by a blue edge that is oriented in the 'y' direction, the direction that is perpendicular to the two cubes.
|
|
| |
| |
The image below shows a three-dimensional projection of the edges of a hypercube. The shadow of the hypercube is the two-dimensional projection that we have been considering above. In a sense the three-dimensional figure is a three-dimensional shadow of the four-dimensional hypercube.
|
|
| |
| |
 |
|
|
|
|
|
Haz hecho público que te gusta. Deshacer
[PDF]
Haz hecho público que te gusta. Deshacer PDF/Adobe Acrobat - Ver en versión HTMLAcknowledgement. This talk was supported by the Ministry of. Education Science and Technology (MEST) and the Korean Federation of Science and ...
Haz hecho público que te gusta. Deshacer
Haz hecho público que te gusta. Deshacer
Haz hecho público que te gusta. Deshacer
Haz hecho público que te gusta. Deshacer
Haz hecho público que te gusta. Deshacer
|
|
|
|
|
64 – DNA – Mayan’s AINTIRAM – NaSSim Haramein – Tesseract – Hypercube
WE ARE THE 99%
DNA says so …
 
The above book DNA AND THE I CHING was published in the 1990s, the youtube interview featuring Nassim Haramein below is recent.
On the cover of the book we see a cube, specifically a 4x4x4 cube comprised of 64 smaller cubes.
If we rotated the cube so we could see only one face, it would appear as a 4×4 square, comprised of 16 squares.
64
Obviously the word ‘amazing’ that Nassim Haramein uses in reference to his epiphany regarding the ancient text Aintiram, does NOT have a best before date that can expire.
Obviously everybody proceeds at their own speed and pace, and what was amazing yesterday to one person, will still be amazing in the future to another person just waking up.
The importance of the number 64
 FRACTALS – KEYHOLE – DNA – ANKH – LAPIS EXILLIS FRACTALS – KEYHOLE – DNA – ANKH – LAPIS EXILLIS
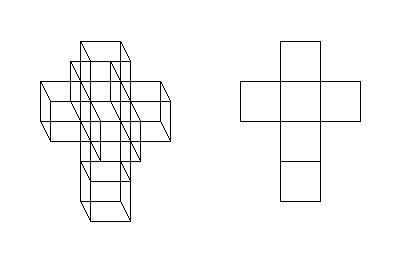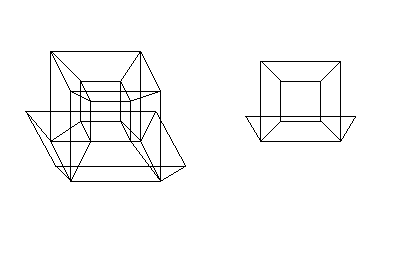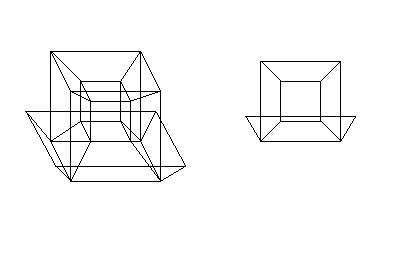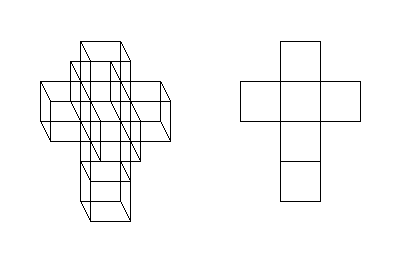
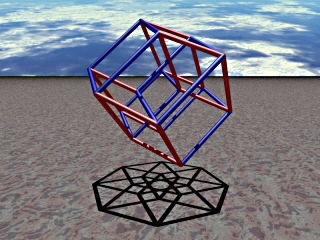
Tesseract – Hypercube – Maltese Cross – Crucifix – cube within the cube – wheels within wheels …
 ‘IN THIS SIGN CONQUER’ the Great Pyramid and the Sacred Cut by Tons Brunés leads us to Nikola Tesla and the Philosopher’s Stone ‘IN THIS SIGN CONQUER’ the Great Pyramid and the Sacred Cut by Tons Brunés leads us to Nikola Tesla and the Philosopher’s Stone

Dalí — Crucifixion (Corpus Hypercubus)According to the Oxford English Dictionary, the word “tesseract” was coined and first used in 1888 by Charles Howard Hinton in his book A New Era of Thought, from the Greek τέσσερεις ακτίνες (“four rays”), referring to the four lines from each vertex to other vertices. Some people have called the same figure a tetracube, and also simply a hypercube (although the term hypercube is also used with dimensions greater than 4).
This is a great great article:
Unfolding the Tesseract an 8-cell
by Peter Turney
http://unfolding.apperceptual.com/

AHA!
I see YHVH trapezoid geometry in the 5 sections of the Cut Cube image on the right.
I see the numbers 5 6 7 8 written on the apex indicative of the corners.
I see a Maltese Cross and a blueprint we can place over the Great Pyramid. (see image/links below)
5 6 7 8 = 26
But here is the wow.
After my neighbor of many years died, his daughter held a contents sale.
I picked up a few items that belonged to John P., one of them was an odd plaque that simply had the numbers 5 6 7 8 placed on it.
It is clear from the items that found their way to me, that ole’ John P. had probably attended some Freemason meetings in his life.
After all he was a cop for 31 years so that does not surprise me.
Nassim Haramein – Sacred Geometry & Unified Fields
Drawing the Hypercube # 1
Tesseract Pencil Visualization
Imagining the Tenth Dimension part 1 of 2

It might help before proceeding to have a quick look at this link first:
http://kachina2012.wordpress.com/2011/12/15/the-sacred-cut-by-tons-brunes/
DNA is the common denominator that links the we are the 99% .
Even the 1% belongs to the 99% as defined by DNA.
note the Friendship Knot that is made by 4 hands in an embrace.
… follow the forearm to the 4 bends in the 4 elbows >>> so what symbol that helps define CW or CCW movement comes to mind?

Does CHASE Bank want to be counted among your friends?

If you do not enjoy this documentary I will refund you your funny Freedom 55 CHASE the money.
REVELATIONS of the PYRAMIDS
 http://www.youtube.com/watch?v=SmnnJytYjpM http://www.youtube.com/watch?v=SmnnJytYjpM
Many AHA to be found among the ruins in that documentary.
Did you know that the first king of Egypt called Menes by the Greeks was know as King AHA!
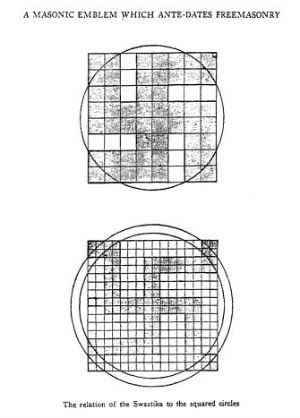
Relationship of both the great pyramid and the swastika to the squared circle, aka pi using two circles?
i.e.
Go to 1:18:20 of that video.
listen carefully to what is being said about the two circles being drawn relative to a square pyramid with eight sides.
Is the speed of light mentioned along with pi?
These next mages were taken out of books printed in and around 1923.
Note in the first image, we have those 4 special constellations mentioned in the documentary, highlighted in the four corners.
i.e. The Man, the Eagle, the Lion, the Bull
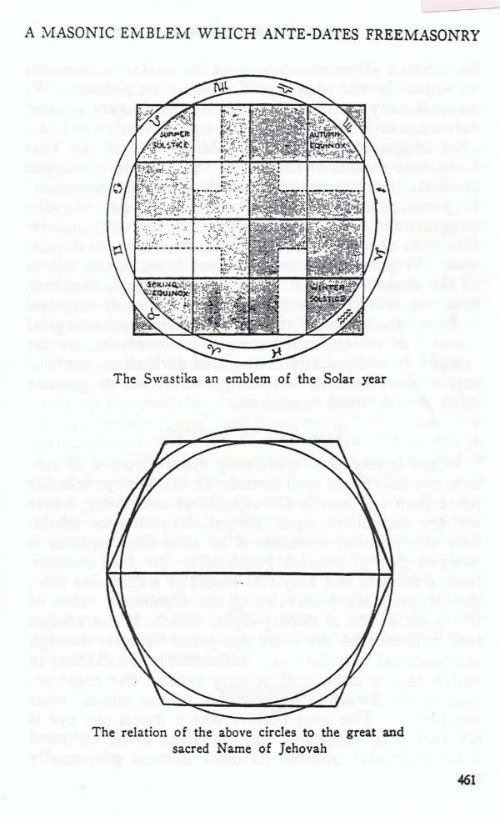
…similar geometry. Is it difficult to connect the star of david to the square or cube?
Not at all.
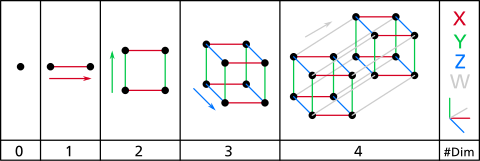
And throughout the video we saw how they divided the Great Pyramid into eight sections, not four.
Go to 16:00 of that video for a discussion of the 8 sided pyramid.
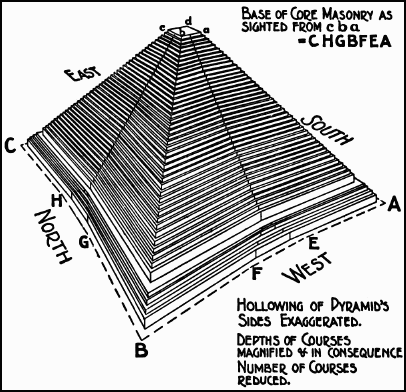
Does the 8 sided pyramid whose 8 sides can only be seen briefly during the two equinoxes have any relationship to the BaB-iLu and the BiBLe?

BaB-iLu is similar to BiBle with the vowels removed…BBL….so is BaBeL, BiBLioS, BaRBeLoS, and the word QiBBLe which is the root of the word CaBaLa.
GeNeSiS is GNoSiS, or both can be written GNSS, if you remove the vowels.
I did promise you an aha or two.
Now you need to find the match to those hexagons/trapezoid in the next image.
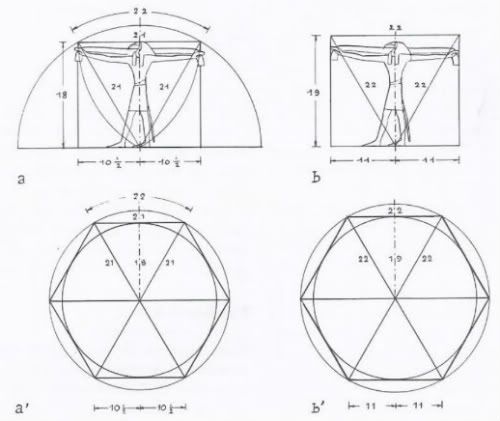
Temple of Man Schwaller de Lubicz page 177 Serpents in the Sky by John Anthony West

.jpg)
WTF 911
WTC 7 is the same shape as the YHVH trapezoid?
YHWH = 26
QaBaLaH =137
Arthur I. Miller ends his book ‘137‘ discussing the ‘26‘ constants physics is currently using trying to formalize a ‘theory of everything’.
Yes 26 of course….and 137 is the most fundamental of them ALL encapsulating 3 other constants into ONE dimensionless constant.
Now would be a good time to introduce the work of engineer Tons Brunes and his insights into geometry.
Specifically ‘the Sacred Cut’.
 http://breakfornews.com/forum/viewtopic.php?p=74451#74451 http://breakfornews.com/forum/viewtopic.php?p=74451#74451
|
|
|
 Primer
Primer
 Anterior
2 a 12 de 27
Siguiente
Anterior
2 a 12 de 27
Siguiente Último
Último
|


![]() FRACTALS – KEYHOLE – DNA – ANKH – LAPIS EXILLIS
FRACTALS – KEYHOLE – DNA – ANKH – LAPIS EXILLIS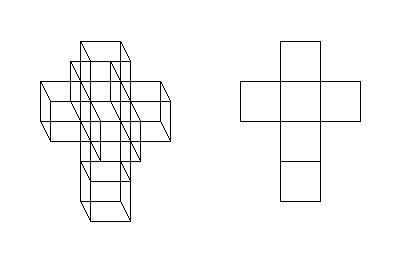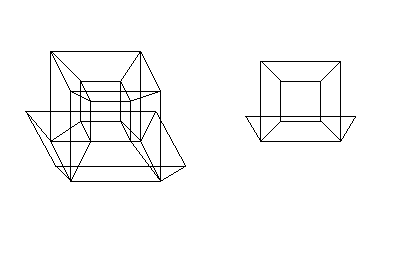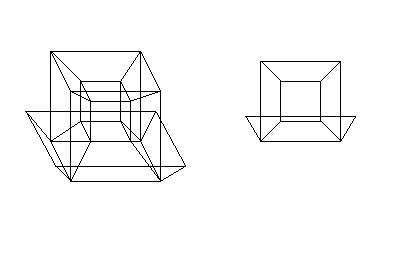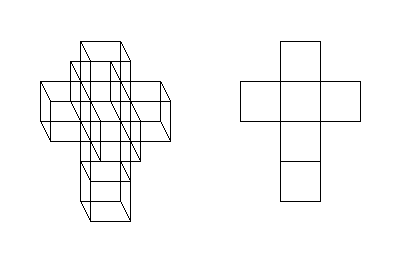




![]() http://www.youtube.com/watch?v=SmnnJytYjpM
http://www.youtube.com/watch?v=SmnnJytYjpM

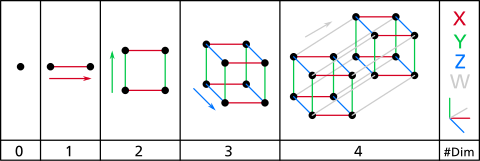



.jpg)
![]() http://breakfornews.com/forum/viewtopic.php?p=74451#74451
http://breakfornews.com/forum/viewtopic.php?p=74451#74451










 1
1

































