–Me encantan las luces de Navidad –exclamó Ven con los ojos llenos de reflejos de colores.
–Sí, son las noches más bonitas del año… –añadió Sal –Bueno, y las de verano cuando vemos en la playa las Perseidas.
–Es verdad, Sal –dijo el pequeño –, pero en Navidad las luces son de todos los colores.
–¿Por qué solo ponemos estas luces tan bonitas en Navidad, Mati? –preguntó el gafotas.
–Parece que su origen podría encontrarse en la época romana, en unas fiestas llamadas los Saturnales –les dijo –que eran muy populares porque en dichas fiestas los esclavos recibían más privilegios que en ninguna época del año. Como las fiestas coincidían con el final de los días más cortos del año, por el solsticio de invierno, lo entendían como el triunfo de la luz sobre la oscuridad y lo celebraban a la luz de velas y antorchas. Fue la popularidad de estas fiestas entre los romanos la que facilitó que los cristianos la asimilaran al nacimiento de su líder para que éstos, los romanos, pudieran convertirse a su religión sin renunciar a sus fiestas alrededor del solsticio.
–Pues sí que es el triunfo de la luz sobre la oscuridad –siguió Ven –, ¡han puesto infinitas luces este año!
–Hala, Ven –protestó Sal –, ya estás exagerando, no puede haber infinitas luces porque no hay infinitas calles y una calle no puede tener infinitas luces.
–Me estás liando… –se quejó Ven agachando su cabecita.
–Mira Ven, si hay un número finito de calles –continuó su hermano con cariño –, por ejemplo, 100 y hubiese infinitas luces en la ciudad, habría en cada calle infinito dividido entre 100 luces en cada calle, y si divides infinito entre un número sale infinito, ¿no?
–¿¿Sí?? –el pequeño abrió los ojos de para en par –¿Infinito dividido entre un número sale infinito?
–Eso es –confirmó Mati –, aunque realmente, infinito no es un número, es un concepto, pero si una cantidad crece mucho, acercándose al infinito, podemos decir que la división entre esa cantidad y un número fijo, se acerca también a infinito.
–No entiendo –confesó el pequeño Ven.
–A ver –dijo Mati –, pensemos en las siguientes divisiones: en el denominador siempre tenemos 100 y los numeradores van aumentando muy rápido, de forma que podemos decir que el numerador tiende a infinito y que , por lo tanto, estas divisiones se están a acercando a ∞ dividido por 100, ¿no?
–Vamos ahora a calcular el valor de esas divisiones –continuó Mati –. La primera sale 1, la segunda sale 100, la tercera sale 10000, y si siguiéramos aumentando el numerador, el resultado iría aumentando tendiendo a ∞:
–Claaaaro… –se asombró el gafotas.
–Por eso podemos decir, con muchas comillas, que ∞ dividido por un número es ∞–les contó.
–¡Toma! –se alegró el pequeño.
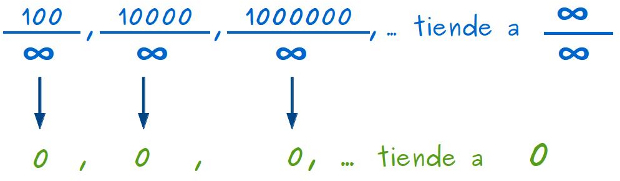
–Ahora vamos a mirar estas divisiones en las que hemos hecho lo contrario –continuó la pelirroja –, hemos dejado fijos los numeradores y hemos ido aumentando los denominadores, para que sean ellos los que tiendan a infinito:
–¿Hacemos las cuentas, Mati? –preguntó el gafotas.
–Adelante, chicos.
–La primera da 1 otra vez –mascullaba Sal –, la segunda da 0,01… la tercera 0,001…
–Eso es, y si siguiésemos aumentando el denominador hasta el infinito, ¿qué pasaría? –les preguntó.
–Que nos saldría casi 0, ¿no, Mati?
–Eso es, Sal, muy bien.
–¡Eres el mejor! –dijo Ven a su hermanito.
–Los dos sois geniales –Mati guiñó un ojo –. Por esto, podemos decir, con muchas muchas comillas, que cualquier número dividido entre ∞ es igual a 0.
–¿Y si divido infinito entre infinito? –preguntó Sal.
–¡Pues 1! –gritó Ven asustando al pobre Gauss.
–Bueno, bueno… –dijo Mati misteriosa –. Vamos a investigar un poco, ¿queréis?
–¡¡Sí!! –gritaron los dos hermanitos.
–Si ponemos en el denominador ∞ y hacemos crecer los numeradores como en el primer ejemplo –les dijo Mati –, podríamos decir que esas divisiones tenderán a ∞ dividido por ∞, ¿no?
–Sí, sí, claro –dijo Ven muy serio.
–Pero al calcular el valor de las divisiones –continuó ella –, como un número dividido entre ∞ hemos dicho que vale 0, tenemos:
–O sea –dijo Ven –que ∞/∞ es igual que 0, ¿verdad, Mati?
–O no… –respondió ella misteriosa –. Vamos a darle la vuelta a a las divisiones, en el numerador ∞ y el denominador creciendo muy rápido:
–¿Qué pasa al calcular el valor de estas divisiones? –les preguntó.
–Infinito dividido por un número es infinito… –decía Sal –. Todas dan como resultado infinito.
–Ajá –confirmó Mati.
–¡Ahí va! –se extrañó Ven –Ahora resulta que ∞/∞ también puede ser infinito…
–¿Cómo sabemos si ∞/∞ es 0 o es infinito?
–U otra cosa, ¿no? –dejó caer Mati misteriosa.
–¿¿Otra cosa?? –exclamó Ven –¡¡Imposible!!
–Fijaos en las siguientes divisiones –les propuso –, ahora hacemos crecer mucho tanto el denominador como el numerador… por lo tanto, también crecerían hasta ∞/∞, ¿no?
–¡Toma, claro! –dijo Ven muy afectado.
–Pues, calculad ahora el valor de las divisiones –les retó —, a ver qué pasa…
–¡Toma, toma, toma! ¡Cómo mola! –gritó Ven de pronto –¡Ahora resulta que ∞/∞ es igual que 3/4!
–Entonces, Mati –preguntó Sal —Si te preguntan cuánto es ∞/∞, ¿qué responderías?
–Que no lo sé, que depende… que es un valor indeterminado, que depende cómo se acerquen al infinito el numerador y el denominador… –les dijo –Es hermoso no saber cómo va a terminar todo en esta vida, ¿no creéis?
–Pues… –dudó Ven y añadió –Sí, es hermoso, a mí me gustan las sorpresas.
















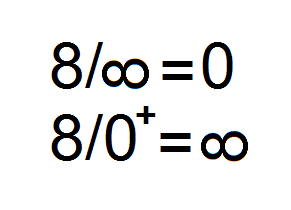

















![PDF] Applying Golden Ratio in Product Packaging and Its Effect on Consumer ' s Buying Behaviour | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/c165da18263b580ae561090171c166c8fa054a6a/3-Figure1-1.png)




![The Pantheon and the golden rectangle [49] | Download Scientific Diagram](https://www.researchgate.net/publication/350876518/figure/fig2/AS:1012713207631873@1618461052910/The-Pantheon-and-the-golden-rectangle-49.png)