|
|
DIAMETRO DE LA TIERRA (MILLAS INGLESAS) =7920=720*11
DIAMETRO DE LA LUNA (MILLAS INGLESAS) =2160=720* 3
RADIO TIERRA MAS RADIO LUNA (MILLAS INGLESAS) =5040=720* 7
7920/5040=11/7 (11 DE SEPTIEMBRE/SEPTIMO/7)
5040*2*22/7=3168*10 (3168=GEMATRIA DE NUESTRO SEÑOR JESUCRISTO)
5040/(7920/2=RADIO DE LA TIERRA)=5040/3960=1.618 (NUMERO DE ORO)
SECRETO 9/11 (TAMBIEN 7/11) ESTA 100% CONECTADO A LA GRAN PIRAMIDE Y LA NUEVA JERUSALEM (MISMO PATRON). La pregunta es del porque de la referencia a la LUNA EN EL MARCO A LA TIERRA. Sabemos que el SOL ES JACOB y que la LUNA ES RAQUEL segun el sueño de Jose de GENESIS 37.
¿Pero la luna en el marco a RAQUEL NO SIMBOLIZA AL HIJO DE RAQUEL? Sabemos que en el sistema solar LA TIERRA ES LA QUE GIRA ALREDEDOR DEL SOL Y LA LUNA GIRA ALREDEDOR DE LA TIERRA.
La simbologia esoterica es como que nos da a ENTENDER QUE LA GRAN PIRAMIDE SIMBOLIZA A LA MADRE Y LA PIEDRA ANGULAR AL HIJO DE LA MISMA. Otro dato asombroso es la interrelacion del PATRON DE LA TIERRA/LUNA/ALQUIMIA CON la misma semana de 7 dias en funcion a la luna y que incluso la cantidad de minutos que contiene la misma equivale matematicamente al RADIO DE LA TIERRA MAS EL RADIO DE LA LUNA.
MENSAJE ESOTERICO-ESPIRITUAL DETRAS DEL 911

Compare estas graficas con el movimiento de la luna.
El movimiento de la Luna es de oeste a este alrededor de la Tierra, en el mismo sentido de rotación del planeta. Veamos cuáles son las fases de la Luna:
 |
- Luna Nueva: en esta fase no vemos ninguna parte iluminada de ella y se da cuando la Luna pasa entre el Sol y la Tierra, siempre siguiendo su órbita alrededor de la Tierra.
- Cuarto Creciente: es cuando la Luna ha completado un cuarto de su órbita alrededor de nuestro planeta y alcanza una posición de 90¼ al este del Sol.
- Luna Llena: una semana después de cuarto creciente, el disco de la Luna se ve completamente iluminado; es decir, con su cara visible frente al Sol.
- Cuarto Menguante: es cuando, una semana después de la fase anterior, solo se ve la mitad del disco de la Luna.
|
Lo que ocurre es que el calendario actual judio, el calendario de Hillel II, considera la luna nueva en luna creciente que como es sabido la misma nace en occidente a contrario de la la verdadera luna nueva que es en luna llena que nace en oriente. Por eso la Biblia habla de "espaldas" porque por razones obvias los judios actualmente en la luna nueva al considerarla en occidente, repito en luna creciente, estan a espaldas de la verdadera luna nueva en luna llena que nace en oriente.
Las cosas nunca suceden sin una mano que las mueva, y en este caso la mano es evidente. Las monedas de los países que fueron agredidos son la clave para la solución de este enigma. Al girarlas toman su ubicación en el pentagrama y anuncian además las fechas de los atentados, pero es solo el comienzo. Todas las investigaciones anteriores han llegado hasta aquí, esta sin embargo comienza en este punto.
 Aquí los signos monetarios toman su lugar en el pentagrama a 0, 90 y 180 grados. Al ser girados las fechas de los crímenes aparecen claramente. Aquí los signos monetarios toman su lugar en el pentagrama a 0, 90 y 180 grados. Al ser girados las fechas de los crímenes aparecen claramente.

Evidentemente hay una fuerte referencia SABATICA EN FUNCION A LA LUNA, EN UN MARCO ALQUIMICO CON EL 911. LA TORA ES EGIPTOLOGIA PURA.
|
|
|
|
|

NOTEN LA LUNA CRECIENTE EN LA PARTE SUPERIOR DEL "HOMBRE DE VITRUBIO"
|
|
|
|
|
http://jesustekton.blogspot.com/
http://jesustekton.blogspot.com/search/label/El%20oficio%20de%20Jes%C3%BAs%20de%20Nazaret
Los evangelios describen a José y a Jesús como un tekton, lo que podríamos traducir como un constructor, fue San Justino, en el siglo II d.C, quién estableció como canónico traducir tekton como carpintero, y desde entonces se asumió como la única verdad esta traducción reduccionista. Esta polémica entre constructores y carpinteros no es poca cosa, el esfuerzo por parte de la ortodoxia de asignar a la familia de Jesús el medio de vida propio del antiguo oficio de los carpinteros ha necesitado de multitud de "églogas" a los trabajadores de la madera. Si se considerasen ambos oficios, no por el aspecto de la importancia actual, sino en el de su etimología respectiva, es bien cierto que los carpinteros y los constructores casi nada tienen en común. Carpintero: constructor de carretas, (Del lat. carpentarius, carpentum, carro en forma de cesto), de donde también provienen el francés "charpentier" y el inglés "carpenter". El latín carpentarius deriva de carpetum (carreta;), palabra de origen céltico, como otras que designan diferentes tipos de carros: "benna", "carrus", "essendum", "petorritum" o "raeda". Tekton: Artífice perteneciente a la construcción o estructura. Perteneciente o relativo a los edificios u otras obras de arquitectura. tekhne TEKS* : ( raiz etimologica indoeuropea.) tejer, fabricar.  En efecto, de manera general en la antigüedad las construcciones eran propias de los tekton, fueran de madera o de piedra. El empleo de la madera correspondía, en las culturas sedentarias, a un estadio inferior que el de la piedra, o, dicho de otra manera, a un menor grado de establecimiento o permanencia en el territorio. Que en la época de Jesús ciertas partes de los edificios se realizasen en madera o en piedra, no significa cambios respecto a las características propias del oficio de tekton. Se puede pues decir que el oficio del tekton, frente al del carpintero, tienen características propias mas allá que la simple cuestión de adaptación de la traducción de una lengua a otra. En la antigüedad un carpintero construía carros o carretas, era un artesano que podía realizar su trabajo en su propio taller, grande o pequeño, y su producto podía ser conducido luego al lugar a donde fuera demandado. Los conocimientos de un carpintero, como hacedor de carros, eran los propios para la realización de las piezas de los carruajes y su ensamblaje, pero muy inferiores a los necesarios por los constructores de edificios, quienes de manera forzosa deberían de manejarse de manera eficaz y completa en disciplinas como el dibujo, la geometría, la aritmética, y las propias de la construcción y la arquitectura. Eran artesanos habituados al uso del martillo, el compás, la plomada y el nivel, herramientas propias de su oficio. Además los constructores de edificios debían de saber manejar los recursos humanos y financieros precisos y necesarios para levantar cualquier edificación independientemente de su tamaño.  Dice Vitruvio en su tratado unos pocos años antes del nacimiento de Jesús: "pues no es posible llegar a ser un diestro arquitecto si posee talento pero carece de conocimientos teóricos, o viceversa. Conviene que sea instruido, hábil en el dibujo, competente en geometría, lector atento de los filósofos, entendido en el arte de la música, documentado en medicina, ilustrado en jurisprudencia y perito en astrología y en los movimientos del cosmos. He aquí las causas de estas exigencias: es conveniente que el arquitecto sea una persona culta y conozca la literatura para fortalecer su memoria con sus explicaciones; conviene que domine el arte del dibujo, con el fin de que, por medio de reproducciones gráficas, le sea posible formarse una imagen de la obra que quiere realizar; también la geometría ofrece múltiples ayudas a la arquitectura, pues facilita la práctica mediante el uso de la regla y del compás, con los que fácilmente se plasman los diseños de los edificios en los solares, mediante los trazados de sus líneas, sus niveles, sus escuadras; gracias a la óptica se sitúan correctamente los puntos de iluminación, según la disposición concreta del cielo; por medio de la aritmética se calculan los costes de los edificios, se hace ver el porqué de sus medidas y mediante el apoyo y el método de la geometría se descifran los difíciles problemas de la simetría; conviene que conozca a fondo la historia ya que, con frecuencia, se emplean abundantes adornos y debe contestar a quien pregunte las razones de sus obras, apoyándose en argumentos históricos." De Architectura. No debemos de olvidar que durante la vida de José, y del propio Jesús, fueron muchos los arquitectos romanos que llevaron a cabo trabajos de construcción de importantes edificios en Galilea y los territorios cercanos: la construcción de la ciudad de Cesárea fundada por Herodes "el grande" antes del nacimiento de Jesús y en honor del emperador Augusto y proyectada según Marco Agripa, la construcción de las ciudades de Séforis y Tiberíades, ambas próximas a Nazaret, y la reconstrucción del segundo Templo de Jerusalén. En estas importantes obras participaron miles de constructores dirigidos por los maestros de obras y arquitectos de Israel, y que el propio Josefo describe que al comienzo de las obras hubo que ocupar 10.000 obreros laicos y 1.000 sacerdotes adiestrados. En la Palestina de los tiempos de Jesús el oficio de tekton alcanzaba un altísimo reconocimiento social, varios eran los oficios que estaban valorados en la cúspide de la estructura social. En el libro: "Jerusalén en tiempos de Jesús" escrito por Joachim Jeremias podemos comprobar como el oficio de tekton era compatible con el de doctor o alto funcionario del Templo: "....Era un signo extraordinario de respeto, porque todo el mundo tenía que saludar a los doctores poniéndose en pie, mientras que los artesanos no estaban obligados a levantarse a su paso durante el trabajo'. "
"La gran estima que se tenía por los artesanos y su trabajo se refleja también en el hecho de que en esta época la mayoría de los escribas ejercía una profesión.....Entre las profesiones que ejercían los más antiguos doctores mencionados en el Talmud figuran las siguientes: sastre, fabricante de sandalias, carpintero, zapatero, curtidor, arquitecto, barquero". pag. 17-18  Más adelante el autor describe que además de doctor, los constructores podían ser sacerdotes. Siendo estos lo que ejecutaban los recintos sagrados. "El segundo templo fue construido en cuarenta y seis años. Herodes el Grande comenzó las nuevas obras en el año 19-20 antes de nuestra Era, y no se terminaron definitivamente hasta el año 62-64 d.C. Josefo dice que, al comienzo de las obras hubo que ocupar 10.000 obreros laicos y 1.000 sacerdotes adiestrados. Aun teniendo en cuenta la continua exageración de Josefo, hay que admitir que se ocupó a un verdadero ejército de obreros. Principalmente se necesitaron canteros, carpinteros, plateros, orfebres y fundidores de bronce. Para la construcción de los sagrados recintos, prohibidos a los laicos, tuvieron que ser utilizados constructores que a la vez eran sacerdotes, es significativo que unos eran expertos en la talla de la piedra ya otros en la carpintería" pag 42 Y como ejemplo de la máxima representación sacerdotal: "Pinjás antes de llegar a ser Sumo Sacerdote, era simple sacerdote rural con el oficio de cantero." pag 212 En resumen, en tiempos de Jesús el oficio de tekton era el propio de los constructores de edificios, este oficio tenía una altísima valoración social y por sus conocimientos y prácticas era muchas veces compartido por sacerdotes, escribas y doctores. Un tekton tenía por su oficio la obligatoriedad de realizar un aprendizaje propio de su disciplina, muy próximo a las enseñanzas que recibían los hombres sabios del templo. Jesús por oficio, y por herencia, compartía conocimientos propios de la clase sacerdotal y en su vida pública hizo demostración practica de todos sus aspectos. Jesús como tekton alcanza la maestría descrita por Vitruvio en su tratado: "Conviene que sea instruido, hábil en el dibujo, competente en geometría, lector atento de los filósofos, entendido en el arte de la música, documentado en medicina, ilustrado en jurisprudencia y perito en astrología y en los movimientos del cosmos."
22.1.08
El apóstol Judas Tomás es nombrado en los evangelios dos veces como uno de los hermanos de Jesús: ¿No es éste el hijo del tekton? ¿No se llama su madre María, y sus hermanos, Jacobo, José, Simón y Judas (Tomás)? (Mt 13,55) ¿No es éste el tekton, hijo de María, hermano de Jacobo, de José, de Judas (Tomás) y de Simón? ¿No están también aquí con nosotros sus hermanas? Y se escandalizaban de él. (Mc 6,3) En el Evangelio, Judas Tomás es llamado varias veces "el Mellizo", en griego, "Dídimo"- (Jn. 11, 16; 20, 24; 21, 2), pero no se aclara de quién era mellizo. Esto ha dado lugar a innumerables hipótesis, incluyendo una que lo hace hermano gemelo de Jesús; por eso en ocasiones se representa a Tomás con los rasgos de Jesús. A Tomás, que es reconocido en los evangelios como hijo de José, de oficio tekton, y hermano de Jesús, de oficio tekton, se le da el oficio de “maestro-tekton" de “arkhitekton”, arquitecto..  Según los "Hechos de Tomás", apócrifo del siglo III, el apóstol Judas Tomás era arquitecto, y habría sido invitado por un rey de la India (Gundoforo, Gondoforo o Gundafar) a levantarle un palacio. Tomás recibe el dinero para la construcción y lo distribuye entre los necesitados. Cuando el rey quiere ver el palacio, Tomás le anuncia que, al dar el dinero a los pobres, le edificó al monarca un palacio en el cielo. El rey, irritado, lo arroja a prisión, pero más tarde lo perdona. A raíz de este episodio legendario, Tomás es representado frecuentemente con una escuadra de arquitecto. Gracias a investigaciones recientes, se han hallado monedas de mediados del siglo I con el nombre del rey Gundafar, lo que da algún sustento histórico a esta tradición. Judas Tomás, arquitecto, celebra su fiesta en el santoral cristiano el 21 de diciembre, día del solsticio de invierno, y una de las puertas del calendario romano del dios Jano, dios de los arquitectos antiguos. A Tomás se le representa con una escuadra de madera, instrumento propio de su oficio, el de arquitecto. Santo Tomás es en la actualidad, y según el santoral católico, patrono de arquitectos; constructores; trabajadores de la construcción; albañiles; agrimensores. Tomás es patrono de los actuales sucesores de los antiguos “tekton”, de los integrantes del gremio del oficio común de su padre José, y de su hermano Jesús.La estirpe del Rey David, de la que descienden José, Jesús y Judas Tomás, es la de los constructores de templos, los constructores del primer templo de Jerusalén. Y el dato cierto del oficio que los tres personajes comparten, y sus conocimientos y su practica en la Galilea de este momento histórico, es un dato que debe incorporarse hoy a cualquier reflexión cristológica.
ECLIPSE EN LA MANO DE ORION EL 21/12/2010 ANTICIPO ESTELARMENTE EL MATRIMONIO REAL DEL PRINCIPE WILLIAM-LA LUNA EN LA MANO SIMBOLIZARIA EL MISMO.
NACIMIENTO DE WILLIAM TAMBIEN FUE EN FUNCION A ORION.
|
|
|
|
|
EL BEBE DEL PRINCIPE WILLIAMS NACIO EN EL MISMO DIA DE MARIA MAGDALENA (22 DE JULIO DEL 2013)-CONTEXTO A LA VISITA DEL PAPA FRANCISCO A BRASIL (BANDERA DE BRASIL ESTA RELACIONADA CON VESICA PISCIS=JUAN 21:11-OJOS DE GATO)-2013=33*61
Así ocurrió
Minuto a minuto: nació el bebé real, hijo de Kate y William
Última actualización: Lunes, 22 de julio de 2013
Para ver las actualizaciones más recientes refresque su navegador o active javascript
-

Este lunes 22 de julio, la duquesa de Cambridge dio a luz al tercer heredero en la sucesión a la corona británica.
El varón pesó tres kilos 900 gramos y nació a las 16:24 hora de Londres.
Así fue la cobertura especial minuto a minuto de BBC Mundo sobre el nacimiento del bebé real, el primogénito del príncipe William y su esposa, Kate.
-
Historia en redes sociales: este es el primer nacimiento real en ser anunciado a través de Twitter y Facebook.
-
Las credenciales y las labores requeridas para una niñera al servicio de la monarquía han cambiado considerablemente a lo largo de los siglos.
-
Un portavoz del Palacio de Buckingham dijo que la reina Isabel II y el duque de Edinburgo estaban encantados con la noticia del nacimiento de su bisnieto.
-

El anuncio oficial fue expuesto en un caballete ornamentado ubicado en el patio delantero del Palacio de Buckingham.
-
Tanto la duquesa como su bebé están en buenas condiciones de salud y permanecerán esta noche en el hospital, según lo anunció el Palacio de Buckingham en un comunicado.
-
-
-

Muchas personas se han congregado frente al hospital St. Mary de Londres a la espera de más noticias.
-
El príncipe Carlos dijo en un comunicado que tanto su esposa Camila como él estaban muy contentos por la llegada de su primer nieto: "Es un momento especial para William y Catherine y estamos muy emocionados por el nacimiento de su bebé".
"Ser abuelo es un momento único en la vida de cualquier persona, como me han dicho muchas personas en los meses recientes, por lo que estoy enormemente feliz de ser abuelo por primera vez y estamos deseando ver al bebé en el futuro cercano", se lee en el texto, que fue publicado a través de la cuenta @ClarenceHouse en la red social Twitter.
-
-
El corresponsal de la realeza de la BBC, Peter Hunt, informó que no se espera que el príncipe William hable esta noche acerca del nacimiento de su hijo. Se espera que pase la noche en el hospital.
-

Frente al palacio de Buckingham también se han acercado los londinenses para festejar la llegada del nuevo heredero a la corona británica.
Se espera que en las próximas horas se anuncie en nombre del niño, que según fuentes médicas está en excelentes condiciones físicas.
-
|
|
|
Fases Lunares para el mes de Julio del año 2013
En el calendario lunar se calculan los años según los ciclos de la luna en lugar de los del sol como se hace en el calendario occidental. En dicho calendario lunar, cada mes lunar corresponde a una lunación, que comprende el período entre dos momentos en que la luna se halla exactamente en la misma fase lunar. Cada mes lunar comprende 29.53 días solares.
Aunque cada día del mes lunar correspondería a una fase lunar, las fases de la luna a las que se conoce con un nombre concreto son la Luna Nueva, Cuarto Creciente, Luna Llena y Cuarto Menguante. Estas fases lunares se asocian a diferentes porcentajes de iluminación o ángulos de fase que van del 0% en la luna nueva, 50% en los cuartos y 100% en la luna llena.
| Día | Fase lunar | Porcentaje iluminado |
| 8 |
Luna Nueva |
En la fase lunar de Luna Nueva la visibilidad es del 0% |
| 15 |
Cuarto Creciente |
En la fase lunar de Cuarto Creciente la visibilidad es del 50% |
| 23 |
Luna Llena |
En la fase lunar de Luna Llena la visibilidad es del 100% |
| 30 |
Cuarto Menguante |
En la fase lunar de Cuarto Menguante la visibilidad es del 50% |
|
|
|
|
|
|
|
|
COLUMBIA, LA LUNA, SOBRE LA PIRAMIDE-DISEÑO DE GIZA EN FUNCION A LA LUNA Y COLUMBIA
Whilst is is obvious that an octagon can be same-sided (lengthwise) as a square - as in Lawlor, above - you need a common describing circle base for an octagon and square to 'live together' on a Seed/Flower of Life geometric development. The octagon sides will have to be smaller than the square's but the radius will be X2 - and hence the describing circle will be X2 in circumference (a Seed/ Flower 'fit'necessity). Lawlor's diagram above might be miscontrued (but not by him!) as indicating Seed/Flower. For my purposes, however, the common side above is abandoned in favour of a common bottom - and (two) circles tangential to each other at it containing two related polygons. One will have a radius of 63 miles (with an inscribed decagon) and one will have a radius of 50.4 miles (with an inscribed octagon), noting that 50.4 is 8/10ths of 63 and that 63 miles is 504 furlongs. Allowing Pi to be 22/7 (which it ain't), we would have circumferences of 316.8 miles (octagon) and 396 miles (decagon) - and our decagon perimeter will (again with 'stylised' 22/7) be 6.66 miles less than the 396 circle circumference. The centre of the octagon circle will fall on Lat. "Pi (22/7)", Elmore Back, River Severn: calc. 7/5.5 = 1.27272727r. The Elmore Back site is on Lat. 51.8428, tan. 1.272728 ...This is very close to the Great Pyramid of Giza gradient. If this latter were on a 9:10 gradient (10/9 = 1.11r), corner to top, say, then the angle would be 51.8442 .... 5184 is a number that is interesting to some: 25920 is the Platonic "canonical" number of years it takes Earth to precess completely through the zodiac (the 12 "Ages" of ...). X 2 = 51840. It is the "Great Year". 5184 is also 72 squared, 72 being a pentagonal and decagonal angle and 1/3 of 2160 ( = 25920/12 = a "canonical Age", itself, aka Great Month). We are looking at some of Bonnie Gaunt's, say, "magnificent numbers" ... this in the octagon and decagon, both. Others include 108, 144, 288, 396, 432, 792 864, 3168, (all 36 X table stuff and you add 0s to each to get interesting (stylised) results: 1080 = Moon's radius, 7920, Earth's diameter, and 864000, Sun's diameter ... and the number of seconds in 10 days, etc.). Note: you have to have "mile" and "second" to get 1080, 7920 and 864000 ... Mile and second appear to be utterly arbitrary man-made quantities of time and distance - but, without them, this beautiful system of number falls apart.*
*
* Take the inch: 198 make a rod/pole/perch (22 X 9) and 198 is half 396, above, our decagon circumference, supposed Ancient Solfeggio healing frequency and Earth radius. Then there's the cricket pitch chain: 792". There has to be a start measure that others are multiplications or divisions off (you might usefully take a look at CIVILISATION ONE, Christopher Knight and Alan Butler, here - thanks Michael!). I note, by-the-by, a fairly standard 51.84 Pi: Taks Planet Earth and shove the Moon atop it tangentially, run an axis from centre Earth X-section to centre Moon Xsection and run a horizontal at 90 degrees to that through the Earth centre/axis bottom, then join up the angles from centre Moon to where the horizontal cuts the Earth circumference, et, voila, Great Pyramid http://genesis.allenaustin.net/pyramid.htm

And the common 'bottom'? It will be at another actual geographical place on a map, too: just by Great Bottom, WhiteSheet Hill, ST813351, Lat 51.115 (a mirror - of sorts). And the 'precious' gems of Lady and Goat? Wel, I gave you Shenstone for Goat/Devil. Lady/Woman is just by Berkeley on the River Severn - a spot from which you might have been able to here the screams of Edward II re. "fundement" and "salamander". Berkeley indicates birch:
COLUMBIA , LA LUNA, SOBRE LA LUNA
|
|
|
|
|
EL ACELERADOR DE PARTICULAS (MAQUINA DE DIOS) ES UN CODIGO ESOTERICO CON FUERTE CONNOTACION CON MARIA MAGDALENA Y EL SANTO GRIAL
AL PAN PAN Y AL VINO TORO
LA CONSTELACION DE LAS PLEYADES ESTA UBICADO EN TAURO/TORO
El diseño del acelerador de particulas tiene forma toroidal, osea de anillo. El toroide tiene fuerte nexo con las PLEYADES/TAURO/TORO. Las pleyades, aparentemente simbolizan la cualidad femenina de DIOS (espiritu santo). La creacion es una cualidad femenina ya que es la mujer la que tiene el hijo y no el hombre. El patriarcado, desgraciadamente, ha obviado este concepto.

El ATLAS (A Toroidal LHC ApparatuS, Aparato Toroidal del LHC) es uno de los cinco detectores de partículas (junto al ALICE, CMS, TOTEM y LHCb) en construcción en el Gran Colisionador de Hadrones, el nuevo acelerador de partículas del CERN en Suiza.
Del ATLAS se espera que investigue los nuevos tipos de partículas que puedan ser detectados en las colisiones de alta energía del LHC, en particular el esquivo bosón de Higgs.
"Estos grupos Sudamericanos han estado trabajando en ATLAS por muchos años, por lo que este es el oficial y bien merecido reconocimiento de su duro trabajo", dijo Jorge Mikenberg, argentino residente en Ginebra, jefe del proyecto del espectómetro de Muones Atlas, que hizo muchos esfuerzos personales para forjar la colaboración con su tierra natal.
Jorge Mikenberg nació en Buenos Aires en 1947. A los 16 años partió hacia Israel y cambió su nombre por Giora. Comenzó a estudiar física entusiasmado por el Prof. Yehuda Shadmi y finalmente recaló en el Instituto de Ciencias Weizmann. En el CERN lo conocen como George.
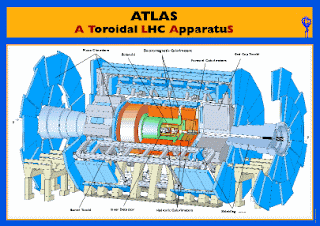
Toroide
De Wikipedia, la enciclopedia libre
En geometría el toroide es la superficie de revolución generada por una curva plana cerrada que gira alrededor de una recta exterior coplanaria (el eje de rotación situado en su mismo plano) con la que no se interseca. Su forma se corresponde con la superficie de los objetos que en el habla cotidiana se denominan donuts,argollas, anillos, aros o roscas. La palabra toroide también se usa para referirse a un poliedro toroidal, la superficie de revolución generada por un polígono que gira alrededor de un eje.[1]
EL NUMERO PI=3.14 TIENE FUERTE NEXO FEMENINO

Animación mostrando un toro siendo cortado por un plano, creando Círculos de Villarceau. Ver Vesica Piscis
El volumen encerrado por un toroide es:
VESICA PISCIS ES SINONIMO DEL NUMERO 153 QUE ESTA EN EL CAPITULO 21 del libro de Juan.
La GRAN PI-RAMIDE diseñada en funcion a las PLEYADES tiene este mensaje espiritual.
STONEHENGE, tambien diseñado en forma circular en funcion a las PLEYADES tambien tiene este mensaje espiritual OBVIAMENTE OBVIADO POR EL CIENTIFICISMO EGOLATRA ATEO que mas busca el PROPIO EGO QUE ADORAR AL CREADOR.
CHICHEN ITZA tambien esta diseñada en funcion a las PLEYADES.
|
|
La alineación del Cenit fue codificada en la Pirámide de Kukulcan. Es simple pero, como mucho de mi trabajo de reconstrucción, ha sido ignorado. El diagrama muestra la verdadera importancia de la Pirámide de Kukulcan y cómo codifica la alineación Precesional Sol-Pléyades-Cenit. (Jenkins)
|
|
|
|
|
|
The Great Pyramid at the Giza Plateau, Egypt, is mysterious, mystical and strategically placed on the face of the Earth. It is aligned with the four cardinal points more accurately than any other structure, even the Greenwich observatory. The builders displayed enlightened understanding of engineering, mathematics, physics and astronomy. They also had a profound knowledge of the Earth's dimensions. Many scientist and scholars now think it was built earlier than the reign of Cheops (Khufu) at 2600 B.C. They disagree with the traditional view of Egyptologist and attribute it to an advanced civilization before the rule of the Pharaohs. I am convinced they are right. For more details follow the "Egypt/Center of Earth" link.
The Pyramid lies in the center of gravity of the continents. It also lies in the exact center of all the land area of the world, dividing the earth's land mass into approximately equal quarters. It lies in the middle of Egypt and in the middle of Lower and Upper Egypt.

The Plate XX from an original 1877 copy of Piazzi Smyth's "Our Inheritance in the Great Pyramid". Charles Piazzi Smyth (1819-1900) was Astronomer Royal for Scotland and a respected Scientist.
The north-south axis (31 degrees east of Greenwich) is the longest land meridian, and the east-west axis (30 degrees north) is the longest land parallel on the globe. There is obviously only one place that these longest land-lines of the terrestrial earth can cross, and it is at the Great Pyramid! This is incredible, one of the scores of features of this mighty structure which begs for a better explanation.
Pyramid Statistics © 2000 by Larry Orcutt,A total of over 2,300,000 blocks of limestone and granite were used in its construction with the average block weighing 2.5 tons and none weighing less than 2 tons. The large blocks used in the ceiling of the King's Chamber weigh as much as 9 tons.
Original entrance of the Great Pyramid. Massive blocks of limestone form a relieving arch over the entrance. 
- The base of the pyramid covers 13 acres, 568,500 square feet and the length of each side was originally 754 feet, but is now 745 feet.
- The original height was 481 feet tall, but is now only 449 feet.
The majority of the outer casing, which was polished limestone, was removed about 600 years ago to help build cities and mosques which created a rough, worn, and step-like appearance. The base measurements of the Great Pyramid are: north - 755.43 ft; south - 756.08 ft; east - 755.88 ft; west - 755.77 ft. These dimensions show no two sides are identical; however, the distance between the longest and shortest side is only 7.8 inches. Each side is oriented almost exactly with the four Cardinal points. The following being the estimated errors: north side 2'28" south of west; south side 1'57" south of west; east side 5'30" west of north; and west side 2'30" west of north. The four corners were almost perfect right angles: north-east 90degrees 3' 2"; north-west 89 degrees 59'58"; south-east 89 deg 56'27"; and south-west
90 deg 0'33". When completed, it rose to a height of 481.4 ft., the top 31 feet of which
are now missing. It's four sides incline at an angle of about 51deg. 51 min. with the ground. At its base, it covers an area of about 13.1 acres. It was built in 201 stepped tiers, which are visible because the casing stones have been removed. It rises to the height of a modern 40-story building.
THE BEDROCK AND CORE
The pyramid is built partly upon a solid, large, bedrock core and a platform of limestone blocks which can be seen at the northern and eastern sides. The builder of this pyramid was very wise to choose this site because most of the stones, with the exception of the casing stones, some granite and basalt stones, could be cut right on the spot and in the nearby quarry. This practical choice made it possible to reduce considerably the time and back-breaking labor needed to drag the stones from distant quarries across the Nile.
The many surveys done on the pyramid proved that the Egyptians located the sides of the pyramid along the four Cardinal Points with extreme accuracy. Whether they used the stars, and/or the rising and setting sun, cannot be determined. One this is certain, that whatever method they used was direct and very simple.
Once the sand, gravel and loose rocks had been removed, down to the solid bedrock of the plateau, the whole pyramid site was open-cast quarried into blocks, leaving a square core for the center of the pyramid (the core is approximately 412.7 ft square, and rises approx. 46.25 feet high). These blocks were then stored outside a low wall; made of mortared stone that surrounds the core (the outside dimensions of the wall are approx. 887.3 feet square). Today there still remains the foundation of this wall on the north, south and west sides of the pyramid, at an average distance of 65 feet from the outer edge of the base casing stone.
This core gives the pyramid stability from the downward and horizontal forces that will develop from the superimposed loads of blocks of stones that are piled up, as the pyramid rises. Also, from the prevailing north-west winds that exert enormous pressures on the huge areas of the pyramid's faces, thus increasing these forces further.
Leveling of the entire pyramid site was accomplished by flooding the area inside the wall with water, leaving just the high spots. These them were cut down to the level of the surface of the water. Next, some of the water was released and the high spots again were cut down to the water's surface. This
process was repeated until the entire pyramid site, between the core and the four walls, was leveled down to the base of the pyramid's platform.
THE CASING STONES
A few of the fine limestone casing blocks remain at the base of the northern side and show how accurately the stones were dressed and fitted together. The core masonry, behind the casing stones, consists of large blocks of local limestone, quarried right on the spot, built around and over the
bedrock core. The size of this core cannot be determined, since it is completely covered by the pyramid.
The casing stones were of highly polished white limestone, which must have
been a dazzling sight. Unlike marble, which tends to become eroded with time
and weather, limestone becomes harder and more polished.
THE SIZE OF THE BLOCKS
The size of the blocks are based on a chance discovery in 1837 by Howard Vyse. He found two of the original side casing blocks at the base of the pyramid, 5 ft x 8 ft x 12 ft, with an angle of 51 degrees, 51 minutes cut on one of the 12 ft. sides. Each of these stones weighed (5 x 8 x 12)/2000 =
39.9 tons before the face angle was cut. These originally were used for the side casing stones of Step No. 1, in the Pascal computer program. The sizes of all the other blocks were scaled from these two original blocks of the remaining Steps 2 to 201.
THE GREAT PYRAMID'S DIMENSIONS AND THEIR LAYOUT
One acre = 43,560 sq. ft, or 208.71 feet on a side.
For the pyramid's base, length = width = (square root of 13.097144 acres) x
208.71 feet = 755.321 feet. Or 755.321 x 12 = 9063.85 inches.
Height = (755.321 x tangent 51deg 51 min)/2 = 480.783 feet. Or 480.783 x 12
= 5769.403 inches.
For the cap stone base: length = width = (32.18 x 2)/tangent 51deg 51 min =
50.55 inches.
The average size of a pyramid stone = (5 x 8 x 12)
The average side measurement, at the base = 759.3 ft.
The height used was 201 steps high, or 480 feet. (This is minus the height
of the Capstone, which was one piece in itself. Geometry of the Great Pyramid
DIMENSIONS of Great Pyramid
The following article is Copyright © 2001-2003 aiwaz.net_institute.
If the calculations concerning the royal cubit are correct the main dimensions of the pyramid should also prove that. The approximate dimensions of the pyramid are calculated by Petrie according to the remains of the sockets in the ground for the casing stones whose remains are still at the top of the pyramid, and the angle 51° 52' ± 2' of the slopes. The base of 9069 inches is approximately 440 royal cubits (the difference is 9 inches which is not a remarkable difference if we consider the whole dimension and consider that the employed data represent only an estimation of the real values) whereas the calculated height, 5776 inches, is precisely 280 royal cubits. The relation 440:280 can be reduced to 11:7, which gives an approximation of the half value of Pi.
Squaring the Circle

The circle and the square are
united through the circumference:
440x4=1760=2x22/7x280
area of square: 440x440=193600
area of circle:28x28x22/7=246400
sum: 440000
|
The engagement of Pi value in the main dimensions suggests also a very accurate angle of 51° 52' ± 2' of the slopes which expresses the value of Pi. Another coincidence is the relation between the height of the pyramid's triangle in relation to a half of the side of the pyramid, since it appears to be the Golden Section, or the specific ratio ruling this set of proportions, F = (sqr(5)+1)/2 = 1.618 = 356:220. This ratio, 356:220 = 89:55 is also contained in the first of Fibonacci Series:
1 2 3 5 8 13 21 34 55 89 144 ...
A single composition contains two apparently contradicting irrational numbers P and F, without disrupting each other. This appears to be completely opposed to the classical architectural canon which postulates that in 'good' composition no two different geometrical systems of proportions may be mixed in order to maintain the purity of design. But analysis of other architectural and artistic forms suggested that the greatest masters skillfully juggled the proportional canons without losing the coherent system, for they knew that these systems can be interconnected if the path that links them is found. That is obvious In the case of the Great Pyramid where two different principles are interweaved without interference ruling different angles of the composition, which is most importantly a most simple one, namely 11:7, a most simple ratio obviously signifying such infinite mysteries as the value of P and most 'natural' value of F. In spite of common miss-understanding of architectural composition, the most mysterious and praised compositions are very simple but not devoid of anthropomorphic appeal, since everything is made out of human proportions, just like Vitruvius describing the rations of the human body, very simple and very clean. The numbers 7 and in 11 are successive factors in the second of Fibonacci progressions that approximate geometry of the pentagram:
1 3 4 7 11 18 29 47 76 123 ...
The summary of the selected main mean dimensions is:
|
dimension
|
b. inch
|
m
|
royal cub.
|
palm
|
digit
|
|
base
|
9068.8
|
230.35
|
440
|
3,080
|
12,320
|
|
height
|
5776
|
146.71
|
280
|
1,960
|
7,840
|
|
sum
|
|
|
720
|
|
20,160
|
|
slope
|
7343.2
|
186.52
|
356
|
2,492
|
9,968
|
|
edge
|
8630.4
|
219.21
|
418
|
2,926
|
11,704
|

The main source of all kinds of delusions and speculations about our mythical past for the western man comes of course from Plato. With the myth of Atlantis he planted the necessary seed of mythical Eden, a culture of high intelligence that lived before the known history. If Plato received any wisdom from the ancient Egypt it could perhaps be traced in the canon of numbers that is so latently present throughout his work, but never on the surface. This canon seems to appear in the descriptions of his fantastic cities where everything is most carefully calculated and proportioned. The topic of Plato's Laws is the description of the ideal state called Magnesia which is entirely composed out of the mysterious number 5,040.
The distance* when Earth is closest to Sun (perihelion) is 147x106 km, which is translated into royal cubits 280x109, hinting at the height of the Great pyramid,
280 royal cubits
|
The Golden Ratio & Squaring the Circle in the Great Pyramid
A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less. [Euclid]
The extreme and mean ratio is also known as the golden ratio.

If the smaller part = 1, and larger part = G, the golden ratio requires that
G is equal approximately 1.6180
Does the Great Pyramid contain the Golden Ratio?
Assuming that the height of the GP = 146.515 m, and base = 230.363 m, and using simple math we find that half of the base is 115.182 m and the "slant height" is 186.369 m
Dividing the "slant height" (186.369m) by "half base" (115.182m) gives = 1.6180, which is practically equal to the golden ration!
The earth/moon relationship is the only one in our solar system that contains this unique golden section ratio that "squares the circle". Along with this is the phenomenon that the moon and the sun appear to be the same size, most clearly noticed during an eclipse. This too is true only from earth's vantage point…No other planet/moon relationship in our solar system can make this claim.
If the base of the Great Pyramid is equated with the diameter of the earth, then the radius of the moon can be generated by subtracting the radius of the earth from the height of the pyramid (see the picture below).

Also the square (in orange), with the side equal to the radius of the Earth, and the circle (in blue), with radius equal to the radius of the Earth plus the radius of the moon, are very nearly equal in perimeters:
Orange Square Perimeter = 2+2+2+2=8
Blue Circle Circumference = 2*pi*1.273=8
Note:
Earth, Radius, Mean = 6,370,973.27862 m *
Moon, Radius, Mean = 1,738,000 m.*
Moon Radius divided by Earth Radius = 0.2728 *
* Source: Astronomic and Cosmographic Data
Let's re-phrase the above arguments **

In the diagram above, the big triangle is the same proportion and angle of the Great Pyramid, with its base angles at 51 degrees 51 minutes. If you bisect this triangle and assign a value of 1 to each base, then the hypotenuse (the side opposite the right angle) equals phi (1.618..) and the perpendicular side equals the square root of phi. And that’s not all. A circle is drawn with it’s centre and diameter the same as the base of the large triangle. This represents the circumference of the earth. A square is then drawn to touch the outside of the earth circle. A second circle is then drawn around the first one, with its circumference equal to the perimeter of the square. (The squaring of the circle.) This new circle will actually pass exactly through the apex of the pyramid. And now the “wow”: A circle drawn with its centre at the apex of the pyramid and its radius just long enough to touch the earth circle, will have the circumference of the moon! Neat, huh! And the small triangle formed by the moon and the earth square will be a perfect 345 triangle (which doesn’t seem to mean much.)
Was the golden ratio intentionally built into the Great Pyramid of Cheops?
Why would anyone intentionally build the golden ratio into a pyramid, or other structure? What was the significance of to the Egyptians? And did the ancient Egyptians intentionally design the Great Pyramid to square the circle?
The answer to these questions is uncertain since designing the Great Pyramid according to the simple rules explained by the graphic below would give the pyramid automatically (by coincidence? ) all its "magic" qualities.
The height of the Great Pyramid times 2π exactly equals the perimeter of the pyramid. This proportions result from elegant design of the pyramid with the height equal two diameters of a circle and the base equal to the circumference of the circle. Click here or on the image below to see larger picture.



For the angle of the Great Pyramid, any theory of the base, combined with any theory of the height, yields a theoretic angle; but the angles actually proposed are the following** :
|
Angle of casing measured
By theory of 34 slope to 21 base
Height : circumference :: radius to circle
9 height on 10 base diagonally
7 height to 22 circumference
area of face = area of height squared
(or sine) = cotangent, and many other relations)
2 height vertical to 3 height diagonal
5 height on 4 base
|
51º 52' ± 2' (51.867)
51º 51' 20"
51º 51' 14.3"
51º 50' 39.1"
51º 50' 34.0"
51º 49' 38.3"
51º 40' 16.2"
51º 20' 25"
|
** Page 184, The Pyramids and Temples of Gizeh
by Sir W.M.Flinders Petrie 1883
Comparing the Great Pyramid with the Pyramid of the Sun in Teotihuacan
The Pyramid of the Sun and the Great Pyramid of Egypt are almost or very nearly equal to one another in base perimeter. The Pyramid of the Sun is "almost" half the height of the Great Pyramid. There is a slight difference. The Great Pyramid is 1.03 - times larger than the base of the Pyramid of the Sun. Conversely, the base of the Pyramid of the Sun is 97% of the Great Pyramid's base.

The ratio of the base perimeter to the height:
| Great Pyramid |
Pyramid of the Sun |
6.2800001... : 1
(deviates by 0.05 % from the
6.2831853 value for 2 x pi) |
12.560171... : 1
(deviates by 0.05 % from the
12.566371 value for 4 x pi) |
The Great Pyramid - Metrological Standard
The Great Pyramid is generally regarded as a tomb and as grandiose memorial to the pharaoh who commissioned it. The opposing view is that of the pyramid being the culminating achievement of those who practiced an advanced science in prehistory.
The Great Pyramid is a repository of universal standards, it is a model of the earth against which any standard could be confirmed and corrected if necessary.
It is exactly the imperishable standard, which the French had sought to create by the devising of the metre, but infinitely more practical and intelligent.
From classical times, the Great pyramid has always been acknowledged as having mathematical, metrological and geodetic functions. But ancient Greek and Roman writers were further removed in time from the designers of the Great Pyramid than they are from us. They had merely inherited fragments of a much older cosmology; the science in which it was founded having long since disappeared.
The Concave Faces of the Great Pyramid

Aerial photo by Groves, 1940 (detail).
In his book The Egyptian Pyramids: A Comprehensive, Illustrated Reference, J.P. Lepre wrote:
One very unusual feature of the Great Pyramid is a concavity of the core that makes the monument an eight-sided figure, rather than four-sided like every other Egyptian pyramid. That is to say, that its four sides are hollowed in or indented along their central lines, from base to peak. This concavity divides each of the apparent four sides in half, creating a very special and unusual eight-sided pyramid; and it is executed to such an extraordinary degree of precision as to enter the realm of the uncanny. For, viewed from any ground position or distance, this concavity is quite invisible to the naked eye. The hollowing-in can be noticed only from the air, and only at certain times of the day. This explains why virtually every available photograph of the Great Pyramid does not show the hollowing-in phenomenon, and why the concavity was never discovered until the age of aviation. It was discovered quite by accident in 1940, when a British Air Force pilot, P. Groves, was flying over the pyramid. He happened to notice the concavity and captured it in the now-famous photograph. [p. 65]
This strange feature was not first observed in 1940. It was illustrated in La Description de l'Egypte in the late 1700's (Volume V, pl. 8). Flinders Petrie noticed a hollowing in the core masonry in the center of each face and wrote that he "continually observed that the courses of the core had dips of as much as ½° to 1°" (The Pyramids and Temples of Gizeh, 1883, p. 421). Though it is apparently more easily observed from the air, the concavity is measurable and is visible from the ground under favorable lighting conditions.

Ikonos satellite image of the Great Pyramid.
Click to view larger image.
I.E.S. Edwards wrote, "In the Great Pyramid the packing-blocks were laid in such a way that they sloped slightly inwards towards the centre of each course, with a result that a noticeable depression runs down the middle of each face -- a peculiarity shared, as far as is known, by no other pyramid" (The Pyramids of Egypt, 1975, p. 207). Maragioglio and Rinaldi described a similar concavity on the pyramid of Menkaure, the third pyramid at Giza. Miroslav Verner wrote that the faces of the Red Pyramid at Dahshur are also "slightly concave."

Diagram of the concavity (not to scale).
What was the purpose for concave Grea the first pyramid should hold true for the others."

Three proposed "baselines" of the Great Pyramid (not to scale).
The purpose for the concavity of the Great Pyramids remains a mystery and no satisfactory explanation for this feature has been offered. The indentation is so slight that any practical function is difficult to imagine.
© 2000 by Larry Orcutt, Catchpenny Mysteries, Reprinted with permission
The Great Pyramid's "Air Shafts"
While shafts in the King's Chamber had been described as early as 1610, the shafts in the Queen's Chamber were not discovered until 1872. In that year, Waynman Dixon and his friend Dr. Grant found a crack in the south wall of the Queen's Chamber. After pushing a long wire into the crack, indicating that a void was behind it, Dixon hired a carpenter named Bill Grundy to cut through the wall. A rectangular channel, 8.6 inches wide and 8 inches high, was found leading 7 feet into the pyramid before turning upward at about a 32º angle. With the two similar shafts of the King's Chamber in mind, Dixon measured a like position on the north wall, and Grundy chiseled away and, as expected, found the opening of a similar channel. The men lit fires inside the shafts in an attempt to find where they led. The smoke stagnated in the northern shaft but disappeared into the southern shaft. No smoke was seen to exit the pyramid on the outside. Three artifacts were discovered inside the shafts: a small bronze grapnel hook, a bit of cedar-like wood, and a "grey-granite, or green-stone" ball weighing 8.325 grains thought to be an Egyptian "mina" weight ball.
Shafts and passages of the Great Pyramid at Giza.
The Shafts of the Queen's Chamber Described
The openings of both shafts are located at the same level in the chamber, at the joint at the top of the second course of granite wall-stone; the ceilings of the shafts are level with the joint.
The northern shaft runs horizontally for just over six feet (76"), then turns upward at a mean angle of 37º 28'. The shaft terminates about 20 feet short of the outside of the pyramid. The total length of the northern shaft is about 240 feet and rises at an angle of 38º for the majority of its length.
The southern shaft also runs horizontally for just over six feet (80"), then turns upward at a mean angle of 38º 28'. The total length of the southern shaft is about 250 feet and, as its northern counterpart, ascends at an angle of 38º for the majority of its length and comes to an end about 20 feet short of the outside of the pyramid.
The Shafts of the King's Chamber Described
The openings of both shafts are located at roughly the same level in the chamber, at the joint at the top of the first course of granite wall-stone. The northern opening is slightly lower, its ceiling being level with the joint, while the floor of the southern opening is roughly level with the joint.
The northern shaft is rectangular, about 7 inches wide by 5 inches high, a shape it maintains throughout its length. The shaft begins on the horizontal for about 6 feet then takes a series of four bends. While maintaining its general upward angle, it shifts first to the north-northwest then back to north, then to north-northeast, and finally back to true north. It has been speculated by some that this unexplained semicircular diversion might have been necessary to avoid some heretofore undiscovered feature of the pyramid. The total length of the northern shaft is about 235 feet and rises at an angle of 31º (with a variation of between 30º 43' and 32º 4') for the majority of its length.
Though the first eight feet of the northern shaft is intact, the next thirty or so feet have been excavated by treasure seekers, presumably following the direction of the shaft in search of treasure. The breach to the shaft was made in the west wall of the short passage leading from the antechamber to the King's Chamber. A modern iron grate today guards the mouth of this breach.
The southern shaft is different in appearance. Its mouth is larger, about 18" wide by 24" high. The dimensions are reduced to about 12" by 18" within a few feet, and then narrows yet more to about 8" by 12". The shape is not rectangular, as is the northern shaft, but has a dome shape where it enters the chamber, with a narrow floor, the angle of the walls being slightly obtuse, and a dome-shaped ceiling. The shaft is horizontal and true south for about 6 feet. At the first bend, its shape changes to an oval, and continues thusly for about 8 feet. Its orientation also changes slightly from true south to south-southwest. At the second bend its shape changes yet again to a rectangle, with a height greater than its width. It retains this shape for the 160 feet to the outside of the pyramid where it emerges at the 101st course of stone. It also changes directions once again at the second bend to a more severe south-southwest diversion. The total length of the southern shaft is about 175 feet and ascends at an angle of 45º (with a variation of between 44º 26' and 45º 30') for the majority of its length.
The Function of the Shafts
When Sandys described the Great Pyramid in 1610, he wrote of the shafts:
In the walls, on each side of the upper room, there are two holes, one opposite to another, their ends not discernable, nor big enough to be crept into -- sooty within, and made, as they say, by a flame of fire which darted through it.
Greaves also wrote of the King's Chamber shafts in 1638. Considering the presence of the lampblack inside, he concluded that the shafts had been intended as receptacles for an "eternal lamp." In 1692, M. Maillet wrote that the shafts served as means of communication for those who were buried alive with the dead king. Not only did the shafts provide air, he reasoned, but they also provides a passage for food which was placed in boxes and pulled through by rope.
By the 20th century, the shafts were presumed to have been designed to provide ventilation. That view has slowly been changing, however. I.E.S. Edwards wrote, "The object of these shafts is not known with certainty; they may have been designed for the ventilation of the chamber or for some religious purpose which is still open to conjecture." (The Pyramids of Egypt, 1961, p. 126.) Ahmed Fakhry wrote, "They are usually referred to as 'air channels,' but most Egyptologists believe that they had a religious significance related to the soul of the king." (The Pyramids, 1969, p. 118.) More recently, Mark Lehner wrote:
A symbolic function should also be attributed to the so-called "air-shafts," which had nothing to do with conducting air. No other pyramid contains chambers and passages so high in the body of masonry as Khufu's and so the builders provided the King's Chamber with small model passages to allow the king's spirit to ascend to the stars. (The Complete Pyramids, 1997, p. 114)
There are many reasons why it is not likely that the shafts were meant for ventilation. The complex angles of the shafts necessitated the piercing of many courses of stone, a daunting logistical challenge during design and construction. Horizontal shafts would have been much easier to build: shafts carved through a single course of stone. One might well wonder why ventilation would be needed at all! No other known pyramid builder made such provisions; even workers in rock-cut tombs managed on the air provided solely by the entrance passage. When the bulk of work on the King's Chamber was being done, ambient air was plentiful as the ceiling had not yet been put in place. The chamber was finished as the superstructure rose.
There are also, however, reasons why it is not likely that the shafts were meant to serve as "launching ramps" for the king's ka. When, in 1964, Alexander Badawy and Virginia Trimble determined that the shafts are "aimed" at certain "imperishable" circumpolar stars and at the constellation of Orion, the function of the shafts as cultic features seemed certain. But the ka did not require a physical means of egress from a tomb -- false doors served this purpose quite nicely both before and after Khufu's reign. The passage that ascends to the entrance of the pyramid is also directed at the circumpolar stars in the manner of previous pyramids. The northern shafts for such a use would have been a needless and bothersome redundancy, although admittedly the Egyptians were not adverse to redundancies.
That fact that no other pyramid in Egypt is known to posses similar shafts as those of the Great Pyramid is problematic. If the shafts were so important for either ventilation or as passages for the king's ka, then why were they omitted in other funerary structures? It is obvious that the builders of Khufu's pyramid went to a jolly lot of trouble to incorporate the shafts into the design of the pyramid, but the true reason why still remains a mystery.
http://genesis.allenaustin.net/pyramid.htm |
|
|
|
|
|
|
|
|
www.youtube.com/watch?v=hBosnQN7usM30 Sep. 2011 - 3 min. - Subido por GuTTedPoSSuM
The Apollo 11 tour has nothing on what is on the dark side of the moon in the Schrodinger ... |
|
|
|
|
www.youtube.com/watch?v=8yaP5-2C4aY21 Oct. 2010 - 4 min. - Subido por Heavens Anomalies JMC
Google Earth Moon Pyramids SPoof. - YouTube. Subscribe 434. All comments ( 22). Share your ... |
www.grahamhancock.com/forum/CreightonS4.php
The Great Pyramid and the Axis of the Earth - Part 2 ... as well as the distance
between the Earth and the moon and the distance between the Earth and the sun
.
greatpyramidmath.weebly.com/19.html
9128.709 inches is the distance between the Great Pyramid's two north side
corner ... The moon is 250000 (one side of a square of One) miles from the earth,
...
www.davidjayjordan.com/Earthmoonphipyramid.html
Plato's Ideal Number = 1x2x3x4x5x6x7 = Earth and Moon Joined = Pyramid
1.618 = Slope = Phi = New Jerusalem. Virgin 7 Pyramid 51.43 degrees = 360 / 7.
https://www.flickr.com/photos/54348064@N08/5035531070/
The geometry of the two circles representing the Earth and Moon are exactly the
ratio of our own Earth and Moon: 7920 miles: 2160 miles. And the geometry of ...
www.numberscience.plus.com/kt2.html
Thus we see an equality between the top height of the Great Pyramid and the
Earth / Moon ratio, which indicates a model for a situation developing under ...
www.numberscience.plus.com/Giza.html
Ancient Mayan city of Teotihuacano - pyramid of the Sun & Moon, Avenue of the
Dead ... Earth in fact has two divine numbers corresponding to it as an object in ...
www.odeion.org/atlantis/chapter-3.html
Mountains of The Moon. 3-8. Earth And Moon. The proportions of the Horizon
Pyramid do indeed relate to the size and ...
www.europa.com/~edge/pyramid.html
The Pyramid is located at the exact center of the Earth's land mass. ... mirrored
surface of 5-1/4 acres distinguished the Pyramid as being visible from the moon.
|
|
|
|
|
|
*The SOHO spacecraft was used to measure the diameter of the Sun by timing transits of Mercury across the surface during 2003 and 2006. The result was a measured radius of 696,342 ± 65 kilometres (432,687 ± 40 miles). Staying within the margin of error, measured radius of the Sun is 432,647 miles (or diameter 865,294 miles).
7 x 8 x 9 x 11 x 12 x 13 = 864,864 which is only 0.05% (430 miles) smaller than the measured value.
Also, 930 x 930 = 864,900 (only 394 miles less than measured value).
Equatorial Circumference of the Earth: 1,000 x 360 x 365.24 feet
= 131,486,400 feet = 40,077km
Official value for equatorial circumference of the Earth: 40,075 kilometers
That is truly a “cosmic” coincidence !!!
There is more… and the Great Pyramid has these values encoded in its proportions!
The radius of the Moon compared to the Earth is three to eleven, ie. 3:11.

Radius of Moon = 1,080 miles = 3 x 360 = 1 x 2 x 3 x 4 x 5 x 6 x (3/2 )
( 1080.030 miles = 1738.1 km )
Radius of Earth = 3,960 miles = 11 x 360 = 1 x 2 x 3 x 4 x 5 x 6 x (11/2)
(3963.167 mi 6378.1 km )
Radius of Earth plus Radius of Moon = 5,040 miles = 14 x 360 =
=1 x 2 x 3 x 4 x 5 x 6 x (14/2) = 7 x 8 x 9 x 10
(Actual 5043.197 miles )
1 x 2 x 3 x 4 x 5 x 6=720
1+2+3+4+5+6 = 21
21 x 240 = 5040
(720 x 21) / 3 = 5040
(720 x 21) / 14 = 1080
The ratio 3:11 is 27.3 percent, and the orbit of the Moon takes 27.3 days.
(Sidereal rotation period 27.321582 d (synchronous).
27.3 days is also the average rotation period of a sunspot.
Here is another unbelievable “coincidence”:
“Pi” approximated to the 9th decimal place is exactly
Pi = 3.141 592 654
3 x 1 x 4 x 1 x 5 x 9 x 2 x 6 x 5 x 4 = 129,600
129,600 x 2 = 25,920 x 10
which is 10x Earth’s precession cycles ( 10 x period of precession of the equinoxes)
The Earth is spinning on its axis in a counter-clockwise direction, and rotating around the sun also in a counter-clockwise direction, while the earth’s spinning axis wobbles like a gyroscope in a clockwise direction. As the result, as the twelve constellations appear to move clockwise along/around the horizon during the course of its annual rotation around the sun during a year, the constellations, from spring or fall equinox to equinox, appear to move counterclockwise at the rate of 72 years/per degree, or one full wobble in 25,920 years (also known as Great Year).of the earth’s axis.
The galactic year is the duration of time required for the Solar System to orbit once around the center of our galaxy (the Milky Way). Estimated length of the galactic year is close to 1000 precession cycles of the Earth.
Fibonacci Sequence, Phi and Pi
The golden ratio is an irrational mathematical constant, approximately 1.6180339887.
phi = 1.61803 39887 49894 84820 45868 34365 63811 77203 09179 80576
phi, 1.618 … is the Golden Ratio in life and the universe.
phi + 1 = phi 2
Phi = 1/phi = 0.618034…
Phi = phi – 1
( 1 + sqrt(5) )/2 = 1.61803 3988…
which is an excellent approximation of Phi
The following formula connects “Pi” (3.14159…) and “phi ” (1.6180…):
(6/5 ) x phi 2 = Pi
or
(12/5) x phi 2 = 2 x Pi
sqrt(phi) nearly equals 4/pi
( 1.272 vs 1.273 )
This Formula is expressed by the numbers describing Pyramids of Giza !!!
Here is how:
Proportions (base to height ratio) of the 1st Pyramid: 11/7
Proportions (base to height ratio) of the 2nd Pyramid: 3/2
Proportions (base to height ratio) of the 3rd Pyramid: 8:/5
(24/10) x phi2 = 2 x Pi
the same formula written with ratios of 3 pyramids:
2 x [ 2 x (11/7)] = (3/2) x (8/5) x phi2
Note: the Great Pyramid is a Golden Pyramid: length of the slope side (356) divided by half of the side (440/2 = 220) height is equal to 1.6181818… which is the Golden Ratio Phi
The dimensions of the Earth and Moon are in Phi relationship, forming a Golden Triangle:

The Summation Series (Fibonacci)
The natural progression follows a “summation series” that is known today as the “Fibonacci Series“ [ of course this Series was in existence before Fibonacci (born in 1179 CE) – he simply “re-discovered” it.] The Summation Series is a progressive series, where you start with the first two numbers, then you add their total to generate the next number, and so on. By definition, the first two Fibonacci numbers are 0 and 1, and each subsequent number is the sum of the previous two. The first summation progression:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …
It is worth to note that the first summation (Fibonacci) progression generates approximation of the golden ratio (PHI):
3/2 =1.5000
5/3 =1.666…
8/5 =1.6000
13/8 =1.6250
21/13=1.6154…
34/21=1.6190…
55/34=1.6176…
89/55=1.61818…
144/89=1.618….
The second of Fibonacci progression (provides approximate geometry of the pentagram and also leads to the golden ratio ‘phi’ )
1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, …
just like in the above example:
199/123 = 1.61788…
322/199=1.618…
…
The Summation Series is reflected throughout nature. The number of seeds in a sunflower, the petals of any flower, the arrangement of pine cones, the growth of a nautilus shell, etc…all follow the same pattern of these series.
The overwhelming evidence indicates that the Summation Series was known to the Ancient Egyptians. Throughout the history of Ancient Egypt, temples and tombs (including pyramids) show in their design expression of the Summation Series: 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, . . .
Pi = 3.141 592 653 5…
3 x 1 = 3
3 x 1 x 4 = 12 (12/3=4)
3 x 1 x 4 x 1 x 5 = 60 (60/12=5)
3 x 1 x 4 x 1 x 5 x 9 = 540 (540/60=9) ::: 540/360=1.5
3 x 1 x 4 x 1 x 5 x 9 x 2 = 1080 (1080/540=2) ::: 1080/360=3 (3/1.5 =2)
3 x 1 x 4 x 1 x 5 x 9 x 2 x 6 = 6480 (6480/1080=6) ::: 6480/360=18 (18/3=6)
3 x 1 x 4 x 1 x 5 x 9 x 2 x 6 x 5 = 32400 (32400/6480=5) ::: 32400/360=90 (90/18=5)
3 x 1 x 4 x 1 x 5 x 9 x 2 x 6 x 5 x 3 = 97200 ::: 97200/360=270 (270/90=3)
3 x 1 x 4 x 1 x 5 x 9 x 2 x 6 x 5 x 3 x 5 = 486 000 ::: 486000/360=1350 (1350/270=5)
Another important observation:
No matter what units of measure we use, the sides of the Giza Pyramids Rectangle (layout for all 3 pyramids)
generate the base of the 1st pyramid:
If we use Royal Egyptian Cubits:
1732/1417 = 440/360

This rectangle shows also relationship of
the Royal Egyptian Cubit 20.62 inch
to the Sacred Cubit 25.2 inch:
1732/1417 = 25.2/20.62
http://blog.world-mysteries.com/science/numbers-dont-lie-ancient-metrology/
|
|
|
|
|
|
|
Another interesting coincidence encoded in the Royal Cubit:
- Royal Egyptian Cubit = 0.524 m
- pi = 3.1416
- 3.1416 feet = 0.957 m = 1.8263 RC
- 2x (0.957 / 0.524 ) = 2x 1.8263 = 3.6526 = 365.26 x 10-2
Number of days in a year: 365.25
Another interpretation of the above:
circumference of a a circle with diameter equal 100 feet is
2 x pi x 100 feet = 2 x pi x 1200? =7539.8? = 365.74 RC
(or 356.25 RC measured in King’s Chamber)
Laws Written in Stone
The Pyramid of Kukulkan in Chichen Itza
Chichen Itza Pyramid Calendar
The Pyramid of Kukulkan at Chichén Itzá, constructed circa 1050 was built during the late Mayan period, when Toltecs from Tula became politically powerful. The pyramid was used as a calendar: four stairways, each with 91 steps and a platform at the top, making a total of 365, equivalent to the number of days in a calendar year.

The ancient Mayan Pyramid at Chichen Itza, Yucatan, Mexico.
Copyright A. Sokolowski
Latitude of the pyramid of Quetzalcoatl: 20° 40? 58.44? N

20 x 40 x 58.44 = 46752
This pyramid is a precise calendar (it has 91 steps on each of 4 sides plus platform on top: 4×91 +1 = 365).
The calendar connection is also confirmed by pyramid’s orientation marking equinoxes and solstices.
The pyramid has 4 sides with 4 staircases dividing each side into 2 sections (in total 8 sections).
Using these numbers and accurate value for 1 year equal 365.25, the pyramid “number” will perfectly relate its latitude:
365.25 x 4 x4 x 8 = 46752
Note: 46752 = 365.25 x 128 (perhaps there is a better fit for the 128?)
For Munck’s number crunching related to the Pyramid of Quetzacoatl in Chichen Itza go to: http://www.world-mysteries.com/chichen_kukulcan.htm

Gate of the Sun at Tiwanacu
The Gate of the Sun is a very sophisticated calendar called “The Muisca Calendar”.

The Gateway of the Sun from the Tiwanku civilization in Bolivia
The Muisca calendar is another important piece in the jigsaw of the lost knowledge of the Andes. If the origins of the Muisca calendar were to be found at Tiwanaku, then perhaps they were also built into the Gate of the this calendar at Tiwanku is not based upon a divison of the solar year into twelve, but into twenty, and this is represented by the eleven smaller icons forming the freize at the bottom which represents the eleven pillars on the west side of the Kalasasayo which is the actual calendar. So if you count from the central icon or pillar out to the right hand end, then back past the central icon to the left hand end, then back to the centre, you will have effectively counted in twenty divisons and followed the path of the sun over a year.
|
|
|
|

This wonderful graphic by Ken Bakeman
shows colored version of the Sun-god
from the Gate of the Sun relief.
Image source: http://www.kenbakeman.com/art.html
So if the chasquis do not relate to the days in whichever number of days we choose for the months of the year, could it be that the chasquis represent the years themselves?
If each chasqui were to represent a solar year, then each column of three chasquis would represent three revolutions of the sun around the eleven pillar calendar wall and three solar years are equivalent to 1 x Muisca Acrotom year of 37 synodic months of 29.53 days and also equivalent to 2 x Muisca Zocam years of 20 sidereal months of 27.32 days.
There are fifteen chasquis on each side of the central figure and each block of 15 chasquis would represent fifteen solar years which would be
5 Muisca Acrotom years of 37 synodic months of 29.53 days or
10 Muisca Zocam years of 20 sidereal months of 27.32 days
The total number of chasquis is thirty chasquis representing thirty solar years which would be
10 Muisca Acrotom years of 37 synodic months of 29.53 days or
20 Muisca Zocam years of 20 sidereal months of 27.32 days
The choice of thirty chasquis as thirty solar years is no random figure, because after thirty solar years have gone by, it becomes necessary to add one sidereal lunar month to the Muisca Zocam calendar making it 20 x 20 + 1 = 401 sidereal lunar months to bring it back into line with the solar year.
At the same time of adding one sidereal month to the Zocam sidereal calendar, it also becomes necessary to add one synodic lunar month to the Muisca Acrotom calendar making it 10 x 37 + 1 synodic lunar months to also bring it into line with both the sidereal lunar calendar and the actual solar year.
Each of the sections with fifteen chasquis corresponds to the period of fifteen solar years which Duquesne tells us was one quarter of the great “century” of the Muiscas so to sum up, each block of fifteen chasquis represents fifteen solar years which is 10 Muisca Zocam years or 5 Muisca Acrotom years, the two blocks together make 30 chasquis representing 30 solar years which is 20 Muisca Zocam years or 10 Muisca Acrotom years and 2 x the 30 chasquis gives 60 chasquis representing 60 solar years completing the great “century” of the Muiscas which was therefore, 40 Muisca Zocam years or 20 Muisca Acrotom years.

Above, detail of the “Gate of the Sun” at Tiwanaku, Bolivia, the 30 Chasquis represent 30 Solar years, equal to 20 Zocam years of 20 sidereal lunar months or 10 Acrotom years of 37 synodic lunar months. At the end of this period, 1 x lunar month had to be added to the lunar calendars to bring them back into phase with the solar year..

Above, the “Gate of the Sun” at Tiwanaku, Bolivia, the 30 Chasquis represent 30 Solar years, equal to 20 Zocam years of 20 sidereal lunar months or 10 Acrotom years of 37 synodic lunar months. At the end of this period, 1 x lunar month had to be added to the lunar calendars to bring them back into phase with the solar year. Beneath the chasquis can be seen the freize with 11 smaller chasqui heads representing the 11 pillars on the calendar wall which in turn divide the solar year into 20 months of 18 days, and the 40 condor heads represent the 40 sidereal months which mesh with the solar calendar every three years.

Above, when the sun reached the end of the pillars, it appeared to “stand still” before beginning its journey back in the opposite direction.
The Great Pyramid of Giza
John Taylor, in his 1859 book “The Great Pyramid: Why Was It Built? & Who Built It?”, claimed that the Great Pyramid was planned and the building supervised by the biblical Noah, and that it was “built to make a record of the measure of the Earth.”

Now let’s look at the coordinates of the Great Pyramid:
29°58? 45.03? N
31°08?03.69?E

Let’s multiply latitude numbers 29x58x45.03 = 75740.46
Now, this pyramid has 4 sides, its perfect slope angle is 51.8428° and there are 365.2425 days in a year:
4 x 51.8428 x 365.2425 = 75740.775
Note: Another very strange “coincidence” was discovered by John Charles Webb Jr. : Precise latitude of the centre of the Grand Gallery (inside GP) is 29°58? 45.28? N = 29.9792458° N
The speed of light in vacuum, usually denoted by c, is a universal physical constant important in many areas of physics. Its value is 299,792,458 metres /s
|
|
|
|
|
|
|
|
¿PORQUE EL NEXO COLUMBIA CON LA "LLEGADA A LA LUNA"? CLAVE GENESIS 8:6 (ARCA DE NOE)
LUNA LLENA EL PRIMERO DE ENERO DE 1972, EN SIRIO, EN EL AÑO NUEVO, (SI-MON/ LUNA PEDRO/PERRO). A LOS 1260 DIAS EXACTOS DE LA LLEGADA A LA LUNA, OSEA EL 31 DE DICIEMBRE DE 1972 FUE EL 11/11 HEBREO (GENESIS 8:6-ARCA DE NOE)-¿MASONES DISEÑARON LA FECHA 20 DE JULIO DE 1969 EN FUNCION A ESTAS PREMISAS? INCLUSO LUNA LLENA EN LA MANO DE ORION, EL 20 DE DICIEMBRE DE 1972. RECORDEMOS EL FUERTE MARCO DE SIRIO EN LA LLEGADA A LA LUNA.
Efectivamente si vamos a las matematicas tenemos que el 20 de junio es el dia numero 201 gregoriano (no bisiesto). Osea que desde este dia hasta el 31 de diciembre tenemos (365-201=164 dias.
20/7/69-31/12/69=164 dias
1970=365 dias
1971=365 dias
1972 (BISIESTO)=366 dias
sumando tenemos:
164+365+365+366=1260 dias exactos.
El patron de secuencia lunar 69, 70, 71 y 72 aproximadamente se repite 88, 89, 90 y 91 y tambien en el 2007, 2008, 2009 y 2010. LAS SECUENCIAS LUNARES SE REPITEN APROXIMADAMENTE CADA 19 AÑOS.
Fases Lunares para el mes de Enero del año 1972
En el calendario lunar se calculan los años según los ciclos de la luna en lugar de los del sol como se hace en el calendario occidental. En dicho calendario lunar, cada mes lunar corresponde a una lunación, que comprende el período entre dos momentos en que la luna se halla exactamente en la misma fase lunar. Cada mes lunar comprende 29.53 días solares.
Aunque cada día del mes lunar correspondería a una fase lunar, las fases de la luna a las que se conoce con un nombre concreto son la Luna Nueva, Cuarto Creciente, Luna Llena y Cuarto Menguante. Estas fases lunares se asocian a diferentes porcentajes de iluminación o ángulos de fase que van del 0% en la luna nueva, 50% en los cuartos y 100% en la luna llena.
| Día | Fase lunar | Porcentaje iluminado |
| 16 |
Luna Nueva |
En la fase lunar de Luna Nueva la visibilidad es del 0% |
| 23 |
Cuarto Creciente |
En la fase lunar de Cuarto Creciente la visibilidad es del 50% |
| 1 |
Luna Llena |
En la fase lunar de Luna Llena la visibilidad es del 100% |
| 8 |
Cuarto Menguante |
En la fase lunar de Cuarto Menguante la visibilidad es del 50% |
|
|
|
|
|
Squaring the Circle - The Great Pyramid
|
The square represents the physical. The circle represents the spiritual. All sacred geometers have attempted the impossible: to square the circle (create a square who's perimeter is equal to the circumference of a circle.)
Here is the first of two valiant attempts:
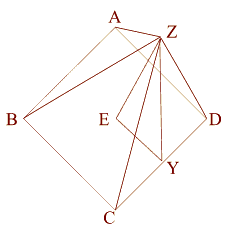
This squaring of the circle works with a right triangle that represents the apothem (ZY) - (a line drawn from the base of the center of one of the sides to top of the pyramid), down to the center of the base (ZE), and out to the point where the apothem touches the Earth (EY).
|

The Great Pyramid of Egypt
(Sphinx in foreground)
|
|
|
Now let's look at this in 2D,
from directly above.
For the purpose of this exercise,
the side (AB) of the base equals 2.
|
|
|
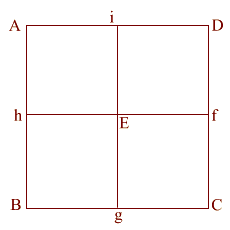
(ABCD) is the base of the Great Pyramid.
This is lettered similarly to the wire frame version (above).
For the purpose of this exercise,
the side (AB) of the base equals 2.
|
|

|
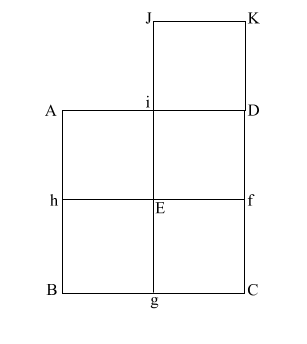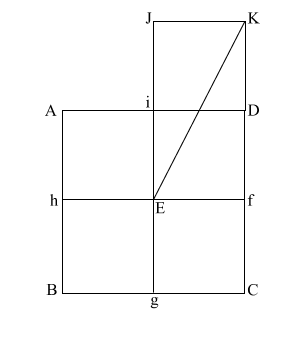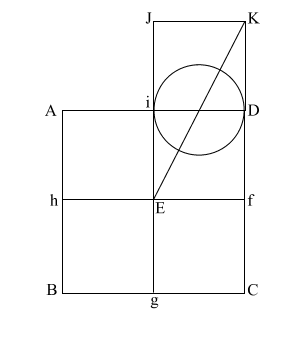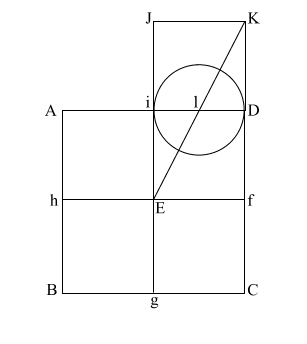
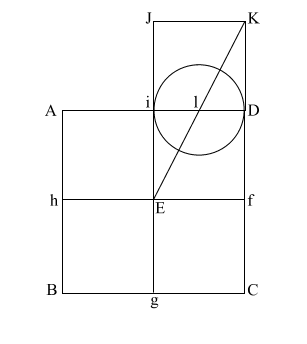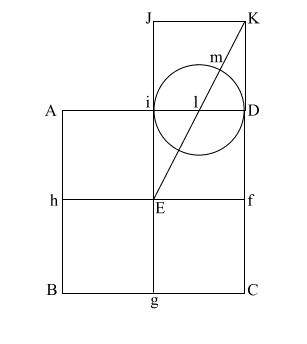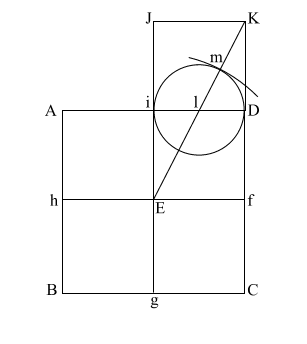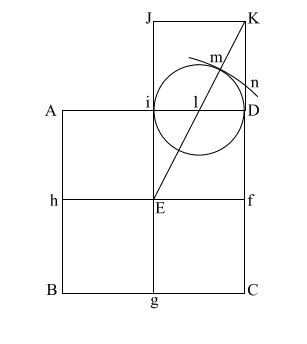
Construct square (i JKD),
thus creating double square (JKE f).
|
|
|
Create diagonal (EK)
which intersects (i D) at (l).
iD = 1,
therefore the diameter
of the circle is also 1.
(EK) = ( 5) = .618 + 1 + .618 5) = .618 + 1 + .618
|
|
|
Put the point of your compass at (E) and extend it along the diagonal (EK) to point (m) where the circle intersects (EK), and draw the arc downward to intersect (KD f C) at (n).
If (EK) = ( 5), and (l m/l D) and l i = .5, the diameter of this circle is 1. 5), and (l m/l D) and l i = .5, the diameter of this circle is 1.
This makes (E m) = .618 + 1, or 1.618.
(E m) is the apothem.
|
|
|
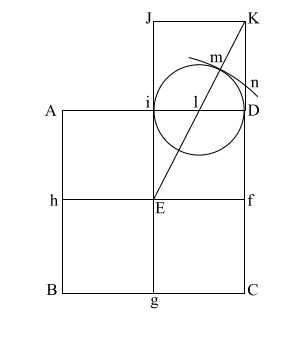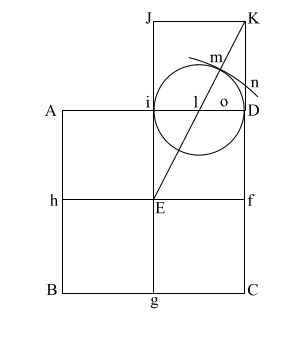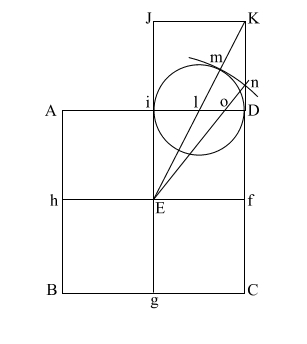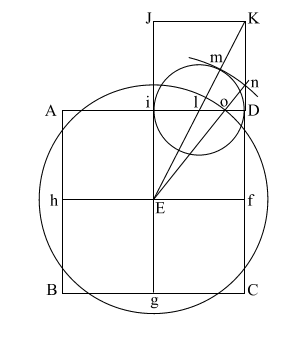
Draw (E n) which intersects (A i l D ) at (o).
Put compass point at (f) and extend it to (n). Again put your point at (E) and draw the circle which happens to have the radius (E o).
(f n) is the height of the Great Pyramid.
This circle comes remarkably close to having the same circumference as the perimeter of the base (ABCD).
|
|
Let's go back to the original right triangle (EYZ)
(EY) = .5
(YZ) = phi
(EZ) = ( phi) phi)
EY = .5, The apothem is phi/1.618. This makes the 51 degree + degree angle.
Using a² + b² = c², this makes the height the square root of phi.
|
Squaring the Circle - The Earth & the Moon
|
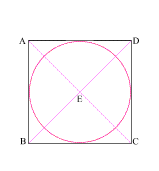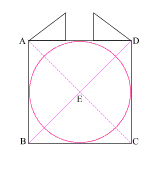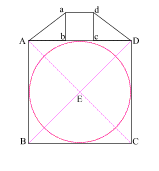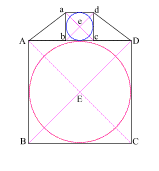
Create a square (ABCD) with (AB) = 11
Create diagonals (AC) and (BD) crossing at center point (E)
Construct a circle which is tangent to square (ABCD) at f
|

|
|
Construct two 3 . 4 . 5 right triangles, with the 4 . 5 angles at (A) and (D).
Connect the 5 . 3 angles creating square (abcd) with side (ab) = 3
{4 + 3 + 4 = 11, or side (AD) of square (ABCD)}
Create diagonals (ac) and (bd) centering at (e)
Create a circle that is tangent to square (abcd) at four places.
|
|
|
Draw line (Ee) which intersects side (AD) at (F)
(EF) = the radius of the larger circle and (eF) = the radius of the smaller circle
The larger circle thus created is to the smaller circle as the moon is to the Earth!
With your compass point at (E), create a circle with radius (Ee)
This creates a circle whose circumference is equal to the perimeter of square (ABCD)!
|

|
The Math:
|
1
(AB) = 11
(EF) = 1/2 of (AB) = 5.5
(ab) = 3
(eF) = 1.5
Therefore 5.5 + 1.5 = 7
The circumference of a circle is equal to two times the radius (the diameter) times pi (3.1416).
C= 14 x 3.1416
C= 43.9824
|
2
In Square (ABCD), (AB) = 11
The perimeter of a square is four times one side. 11 x 4 = 44
According to the Cambridge Encyclopedia, the equator radius of the Earth is 3963 miles. The equator radius of the Moon is 1080.
The claim is that the smaller circle (in square abcd) is to the larger circle (in square ABCD) as the Moon is to the Earth.
|
|
3
(EF) = 5.5
(F e) = 1.5
5.5 : 1.5 :: 3963 : 1080
5.5 / 1.5 = 3.66666
3963 / 1080 = 3.6694 - (if it had been 3960, it would have been exact!)
|
|
|
|
|
|
EN EL MISMO PATRON MATEMATICO DE LA CUADRATURA DEL CIRCULO, ESTA CODIFICADA LA FESTIVIDAD DE JANUKAH. NOTEN LA REFERENCIA A LA LETRA J Y LA LETRA K. EN ESTE CONTEXTO LA ESCUADRA Y EL COMPAS MASONICO TIENE ESTA REFERENCIA
Squaring the Circle - The Great Pyramid
|
The square represents the physical. The circle represents the spiritual. All sacred geometers have attempted the impossible: to square the circle (create a square who's perimeter is equal to the circumference of a circle.)
Here is the first of two valiant attempts:
This squaring of the circle works with a right triangle that represents the apothem (ZY) - (a line drawn from the base of the center of one of the sides to top of the pyramid), down to the center of the base (ZE), and out to the point where the apothem touches the Earth (EY).
|

The Great Pyramid of Egypt
(Sphinx in foreground)
|
|

|
Now let's look at this in 2D,
from directly above.
For the purpose of this exercise,
the side (AB) of the base equals 2.
|
|

|
(ABCD) is the base of the Great Pyramid.
This is lettered similarly to the wire frame version (above).
For the purpose of this exercise,
the side (AB) of the base equals 2.
|
|

|
Construct square (i JKD),
thus creating double square (JKE f).
|
|

|
Create diagonal (EK)
which intersects (i D) at (l).
iD = 1,
therefore the diameter
of the circle is also 1.
(EK) = ( 5) = .618 + 1 + .618 5) = .618 + 1 + .618
|
|

|
Put the point of your compass at (E) and extend it along the diagonal (EK) to point (m) where the circle intersects (EK), and draw the arc downward to intersect (KD f C) at (n).
If (EK) = ( 5), and (l m/l D) and l i = .5, the diameter of this circle is 1. 5), and (l m/l D) and l i = .5, the diameter of this circle is 1.
This makes (E m) = .618 + 1, or 1.618.
(E m) is the apothem.
|
|

|
Draw (E n) which intersects (A i l D ) at (o).
Put compass point at (f) and extend it to (n). Again put your point at (E) and draw the circle which happens to have the radius (E o).
(f n) is the height of the Great Pyramid.
This circle comes remarkably close to having the same circumference as the perimeter of the base (ABCD).
|
En otra clave o significado, "niños", Esotéricamente, son los "Iniciados", y, a quienes, se refiere nuestro Señor Jesús el Cristo:
"... De cierto os digo, que si no os volviereis, y fuereis como niños, no entraréis en el reino de los cielos." (Mateo, 18: 3).
Si la voz de un niño inocente es escuchada y acogida en los Cielos, cuanto más la voz de un Iniciado, la voz de un verdadero esoterista que se ha vuelto como un niño, y es como un niño...
JANUCÁ HANUKKÁH O CHANUKÁH
ES LA FIESTA DE LA DEDICACIÓN - LA FIESTA DE LAS LUCES
“zot chanukat ha-mizbe'ach.”
"Esta fue la dedicación [hanukkáh] del altar".
(Números 7: 84, 88).
El Rey Salomón dice en "Proverbios":
"Educad [chanoch] a un niño de acuerdo a su naturaleza;
cuando él crezca él no la abandonará."
"Y se hacía la fiesta de la dedicación [Hanukkáh] en Jerusalem; y era invierno;
Y Jesús andaba en el templo por el portal de Salomón.
Y rodeáronle los Judíos y dijéronle: ¿Hasta cuándo nos has de turbar el alma?
Si tú eres el Cristo, dínoslo abiertamente.
Respondióles Jesús: Os lo he dicho, y no creéis: las obras que Yo hago en nombre de Mi Padre, ellas dan testimonio de Mí;
Mas vosotros no creéis, porque no sois de Mis ovejas, como os he dicho.
Mis ovejas oyen Mi voz, y Yo las conozco, y Me siguen;
Y Yo les doy vida eterna y no perecerán para siempre,
ni nadie las arrebatará de Mi mano.
Mi Padre que me las dió, mayor que todos es
y nadie las puede arrebatar de la mano de Mi Padre.
Yo y el Padre una cosa somos."
(Juan, 10: 22-30).
La palabra Hebrea Chanukkáh o Hanukkáh", ("dedicación", "consagración"), proviene del Hebreo "hanakh" ("entrenamiento"), significando a su vez: "dedicar", "dar", "empezar", "comenzar".
El Hebreo "Hanokh" o "Henoch", significa también "dedicado, consagrado", "Iniciado", y viene asimismo de la palabra "hanakh".
La palabra Hebrea "Chanoch" o "Hanokh" ("Henoch"), tiene el mismo significado que la palabra Hebrea "HANUKKÁH", y vienen de la misma raíz Hebrea "hanakh", y por lo tanto, son sinónimos.
JANUKAH-RELACION CON LA ESCALERA DE JACOB/CUADRATURA DEL CIRCULO/ALQUIMIA ENTRE EL CIELO Y LA TIERRA-LA GEMATRIA DE MESIAS ES IGUAL A LA DE SERPIENTE (NUMERO 358)
El Mes de Kislev
Jánuca: Los Significados Ocultos del Dreidel
De una monografía del rabino Ginsburgh acerca del dreidel (trompo, perinola)
Jánuca y el Dreidel : La Unión de lo Sobrenatural y lo Natural
Encendemos las luminarias de Jánuca para difundir el milagroso poder de Dios que intervino en beneficio de los Macabeos. Los ocho días de Jánuca conmemoran el encendido milagroso de los siete brazos de la Menorá en el Templo Sagrado durante ocho días, conectando de esta manera los números 7 y 8. En la tradición judía, el número 7 representa un estado de perfección natural, por ejemplo el Shabat es el séptimo día de la semana, pero el número 8 representa un estado de perfección sobrenatural, como la circuncisión que es hecha en el niño de ocho días de vida. Entonces Jánuca reúne lo natural con lo sobrenatural, lo finito y lo infinito.
El Baal Shem Tov, fundador del movimiento jasídico, tenía un amor y afinidad especial por Jánuca más que por las otras festividades del año. Esto es así porque las velas de esta festividad representan el don innato del alma judía de esparcir luz e iluminar el mundo entero, incluso las naciones del mundo. El mensaje del Baal Shem Tov diseminado por el alma judía pone de relieve dos conceptos complementarios: que Dios crea la naturaleza de nuevo a cada momento y al mismo tiempo la impregna con un poder sobrenatural. Gracias a esta capacidad de unir lo natural y lo sobrenatural, la luz de las velas de Jánuca dará lugar eventualmente a la redención verdadera y completa.
El Dreidel
Una costumbre judía muy popular es jugar en Jánuca con el dreidel , también llamado trompo, perinola, etc. Juntos adultos y niños se reúnen alrededor de las luces de la menorá, girando la perinola para descubrir qué letra sale. ¿Cuál es el significado profundo de este acto, y qué pensamientos significativos podemos tener en mente mientras jugamos con el dreidel este Jánuca? Como veremos, al tirar la perinola frente a las luces de las candelas, estamos salvando las distancias entre la realidad finita y la infinita.
Las Cuatro Letras del Dreidel
Tradicionalmente el dreidel tiene cuatro caras. Lo primero que notamos es que cada una tiene grabada una letra del alfabeto Hebreo: nun ( נ ), guimel ( ג ), hei ( ה ) y shin ( ש ), las iniciales de la frase “Un gran milagro ocurrió allí”, nes gadol haiá sham . ( Zejariá 6:12)
Es de destacar que el valor numérico de las cuatro letras es 358, el valor numérico de Mashíaj, משיח ! El motivo recurrente que encontramos en los significados ocultos del dreidel , es el Mashíaj y la redención, cambiar el mundo y hacerlo una morada adecuada para el Creador.
En las generaciones pasadas, algunos judíos que vivían en la Tierra de Israel decidieron que era apropiado cambiar la última letra de “allá” (sham) por “aquí” (po), transformando la frase de acuerdo a estas iniciales en “Un gran milagro ocurrió aquí”. Según esta idea, las letras del dreidel, nun, guimel, hei, pei , suman 138, el valor de Menajem, uno de los nombres del Mashíaj de acuerdo con nuestros sabios; y es también el valor de la palabra Tzemaj el nombre del Mashíaj que aparece en el Tana'j “Tzemaj es su nombre…”
Cuando el Cuadrado se transforma en un Círculo
El dreidel tiene la forma de cono, con cuatro caras cuadradas y un cono cuya punta inferior puede dar vueltas. Hacerlo girar causa que sus contornos cuadrados desaparezcan redondeando sus aristas.
Conceptualmente, sus caras y aristas cuadradas representan la lógica matemática y silogística de la antigua Grecia, sobre las cuales triunfaron los Macabeos tanto material como espiritualmente. Los Macabeos, fieles a nuestra fe en un Dios, creían y sobre todo llevaban a la práctica su creencia de que una visión de la vida y la naturaleza basada sólo en el racionalismo humano es insuficiente. Porque hay además un Dios infinito que trae la realidad a la existencia sin límites. Entonces, los contornos redondeados revelados por el dreidel al girar representa el reino de lo Divino, que se manifiesta en forma de milagros, aquellos eventos que no pueden ser comprendidos e incluso a veces no pueden ser percibidos por la mente humana racional. 1
Utilizando la terminología del Jasidut, los contornos redondeados del dreidel girando representa la revelación de la luz abarcadora de Dios, refiriéndose a la energía con la cual el Todopoderoso sostiene la realidad. Este aspecto de Dios es descripto como circular porque Él sustenta a toda la realidad por igual, desde la partícula más diminuta hasta el cúmulo más enorme de galaxias. Así como el círculo no tiene arriba y abajo y todos los puntos de su circunferencia son equivalentes, desde la perspectiva de la luz abarcadora de Dios abarcadora o circundante de Dios, toda la realidad tiene igual importancia y es sostenida permanentemente. Así como Dios establece las leyes de la naturaleza, sólo Él tiene el poder de alterarlas.
En contraposición, la forma cuadrada del dreidel representa la experiencia constante de la luz interior de Dios, refiriéndose a la energía con la cual el Todopoderoso es percibido por nuestra conciencia. En otras palabras, es la capacidad de revelar las diferentes formas en que la Divinidad se inviste en las distintas partes de la naturaleza, según la diferente capacidad de percibir a Dios que tiene cada individuo. Por esta razón, la luz interior de Dios está asociada con una línea recta (como las del contorno de las caras del dreidel ), que tienen un principio y un final, que indica la existencia de una gradación.
La luz abarcadora o circundante (redonda) revela la naturaleza infinita de Dios; la luz interior (cuadrada) revela Su naturaleza finita. Los milagros suceden a partir de la luz abarcadora de Dios, desde Su naturaleza infinita.
Entonces nosotros no somos los únicos que jugamos con el dreidel . En cierto sentido, siempre que ocurre un milagro nos podemos imaginar que Dios también está jugando con Su enorme dreidel cósmico. Al girar este dreidel abstracto, Dios le da vueltas a Su luz interior, a Su naturaleza finita revelada tal como la experimentamos normalmente, difumando las reglas lógicas estrictas que gobiernan la realidad y permitiendo que Su naturaleza infinita se revele. Podríamos decir que Dios está continuamente haciendo girar los milagros en la naturaleza.
Al meditar en el acto de tirar nuestro propio dreidel de madera, nos conectamos e identificamos con lo Divino y demostramos nuestro deseo de ver más allá de la faceta cuadrada y lógica de la naturaleza. Creer y conectarnos con el reino infinito y circular del espacio infinito de Dios. En efecto, meditar en el giro del dreidel tiene el poder de abrir nuestros ojos a los milagros.
|
|
|
|
|
Phi and the Solar System
The dimensions of the Earth and Moon are in Phi relationship, forming a Golden Triangle

The illustration above shows the relative sizes of the Earth and the Moon to scale.
- Draw a radius of the Earth (1)
- Draw a line from the center point of the Earth to the center point of the Moon (square root of Phi)
- Draw a line to connect the two lines to form a Golden Triangle (Phi).
Using dimensions from Wikipedia and geometry’s classic Pythagorean Theorem, this is expressed mathematically as follows:
| |
Dimension
(km) |
Proportion
(Earth=1) |
Mathematical
Expression |
| Radius of Earth |
6,378.10 |
1.000 |
A |
| Radius of Moon |
1,735.97 |
0.272 |
|
| Earth + Moon |
8,114.07 |
1.272 |
B |
| Hypotenuse |
10,320.77 |
1.618 (Φ) |
C |
Hypotenuse /
(Earth Radius +
Moon Radius) |
1.618 (Φ) |
|
A²+B²=C² |
This geometric construction is the same as that which appears to have been used in the construction of the Great Pyramid of Egypt.
Source: Hidden Nature by Alick Bartholomew. Thanks to Sathimantha Malalasekera for bringing this to my attention.
Certain solar system orbital periods are related to phi
 Certain planets of our solar system seem to exhibit a relationship to phi, as shown by the following table of the time it takes to orbit around the Sun: Certain planets of our solar system seem to exhibit a relationship to phi, as shown by the following table of the time it takes to orbit around the Sun:
| |
Mercury |
Venus |
Earth |
Jupiter |
Saturn |
| Power of Phi |
-3 |
-1 |
0 |
5 |
7 |
| Decimal Result |
0.24 |
0.62 |
1.0 |
11.1 |
29.0 |
| Actual Period |
0.24 |
0.62 |
1.0 |
11.9 |
29.5 |
Saturn reveals a golden ratio phi relationship in several of its dimensions

The diameter of Saturn is in a phi relationship with the diameter of its rings, as illustrated by the green lines.The inner ring division is in a phi relationship with the diameter of the rings outside the sphere of the planet, as illustrated by the blue lines.The Cassini division in the rings of Saturn falls at the Golden Section of the width of the lighter outside section of the rings.
Note: Phi grid showing Golden Ratio lines provided by PhiMatrix software.
A closer look at Saturn’s rings reveals a darker inner ring which exhibits the same golden section proportion as the brighter outer ring.

Venus and Earth reveal a golden ratio phi relationship
Venus and the Earth are linked in an unusual relationship involving phi. Start by letting Mercury represent the basic unit of orbital distance and period in the solar system:
| Planet |
Distance
from
the sun
in km (000) |
Distance
where
Mercury
equals 1 |
Period
where
Mercury
equals 1 |
| Mercury |
57,910 |
1.0000 |
1.0000 |
| Venus |
108,200 |
1.8684 |
2.5490 |
| Earth |
149,600 |
2.5833 |
4.1521 |
Curiously enough we find:
Ö Period of Venus * Phi = Distance of the Earth
Ö 2.5490 * 1.6180339 = 1.5966 * 1.6180339 = 2.5833

In addition, Venus orbits the Sun in 224.695 days while Earth orbits the Sun in 365.242 days, creating a ratio of 8/13 (both Fibonacci numbers) or 0.615 (roughly phi.) Thus 5 conjunctions of Earth and Venus occur every 8 orbits of the Earth around the Sun and every 13 orbits of Venus.
Mercury, on the other hand, orbits the Sun in 87.968 Earth days, creating a conjunction with the Earth every 115.88 days. Thus there are 365.24/115.88 conjunctions in a year, or 22 conjunctions in 7 years, which is very close to Pi!
See more relationships at the Solar Geometry site.
Relative planetary distances average to Phi
The average of the mean orbital distances of each successive planet in relation to the one before it approximates phi:
| Planet |
Mean
distance
in million
kilometers
per NASA |
Relative
mean
distance
where
Mercury=1 |
| Mercury |
57.91 |
1.00000 |
| Venus |
108.21 |
1.86859 |
| Earth |
149.60 |
1.38250 |
| Mars |
227.92 |
1.52353 |
| Ceres |
413.79 |
1.81552 |
| Jupiter |
778.57 |
1.88154 |
| Saturn |
1,433.53 |
1.84123 |
| Uranus |
2,872.46 |
2.00377 |
| Neptune |
4,495.06 |
1.56488 |
| Pluto |
5,869.66 |
1.30580 |
| Total |
|
16.18736 |
| Average |
|
1.61874 |
| Phi |
|
1.61803 |
| Degree of variance |
|
(0.00043) |
Note: We sometimes forget about the asteroids when thinking of the planets in our solar system. Ceres, the largest asteroid, is nearly spherical, comprises over one-third the total mass of all the asteroids and is thus the best of these minor planets to represent the asteroid belt. (Insight on mean orbital distances contributed by Robert Bartlett.)
2005 unveiled the discovery of a 10th planet called 2003UB313. It was found at a distance of 97 times that of the Earth from the Sun. Its ratio to Pluto would thus be 2.47224, much higher than any previous planet to planet orbital distance ratio. Could it be that this is actually the 11th planet and the 10th planet will be found at an orbit whose ratio is 1.52793 times that of Pluto, preserving the phi average? Time will only tell, but if it happens remember that you heard it here first.
The shape of the Universe itself is a dodecahedron based on Phi
New findings in 2003 based on the study of data from NASA’s Wilkinson Microwave Anisotropy Probe (WMAP) on cosmic background radiation reveal that the universe is finite and shaped like a dodecahedron, a geometric shape based on pentagons, which are based on phi. The the Universe page for more.
|
|
|
|
|
TEOTIHUACAN-GIZE-NUMERO DE ORO PHI=1.618-RELACION CON LA INDEPENDENCIA DEL ESTADO DE ISRAEL
ISRAEL
ISIS
RA
ELOHIM
330 AÑOS EXACTOS MAS 1618=1948 (INDEPENDENCIA DE ISRAEL)





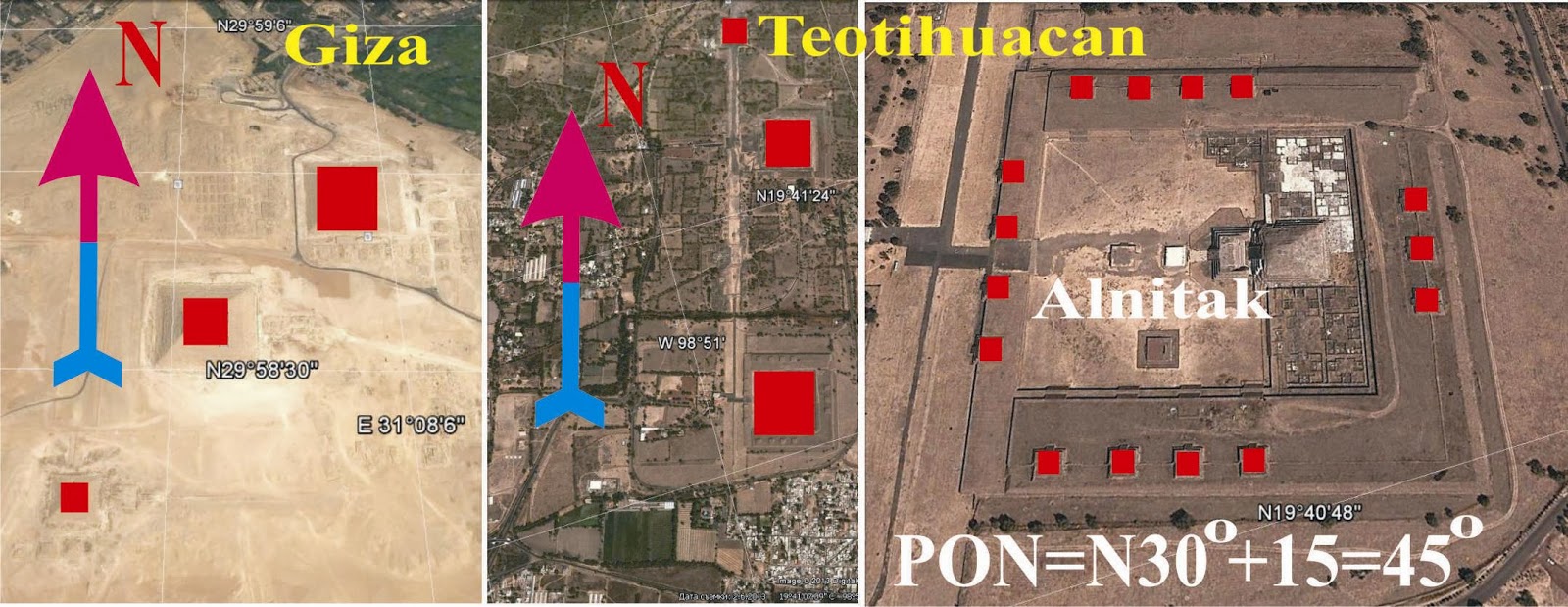
¿Qué es phi?
Phi y la serie de Fibonacci
Funciones trigonométricas
Razones matemáticas
Pentágono
Espirales Áureas
Inicio :: Ver temas relacionados: Decalogo Geometria Sagrada :: Número de Oro :: Merkaba
¿Qué es phi?
Phi (1.618033988749895... ), pronunciado como fi, es un numero irracional como Pi ( 3.14159265358979... ), pero con muchas características matemáticas inusuales. Phi es la base de la Proporción Dorada. La razón o proporción determinada por Phi (1.618...) era conocida por los Griegos como la “Sección Dorada” y por los artistas del renacimiento como la “Proporción Divina”. También se le conoce como la razón Dorada o la Proporción Áurea.
Phi, como Pi, es una razón definida por una construcción geométrica.
Pi es la relación de la circunferencia de un círculo respecto a su diámetro. Phi es la proporción de los segmentos de una línea que resultan cuando una línea es dividida de una forma única y especial.
La línea es dividida para que la proporción de la longitud de la línea entera (A) respecto a la longitud del segmento de la línea mayor (B) sea igual que la proporción de la longitud del segmento de la línea mayor (B) a la longitud del segmento de la línea menor (C)

Esto es que A es 1.618... veces B, y B es 1.618… veces C. Recíprocamente, C es 0.618... de B y B es 0.618... de A. Phi con mayúscula "Phi" es 1.6180339887..., mientras que phi con minúscula es 0.6180339887, el reciproco de Phi o Phi menos 1.
Lo que hace a phi incluso mas inusual es que puede derivarse de muchas formas y ser encontrado en proporcionalmente en el universo. Phi F puede ser derivado por: la serie numérica descubierta por Leonardo Fibonacci, matemáticas y geometría.
Phi y la serie de Fibonacci
Leonardo Fibonacci, por herencia del mundo árabe, descubrió la serie que nos lleva a phi. En el siglo XII, Leonardo Fibonacci descubrió una serie numérica simple que es la base de la increíble relación que encontramos detrás de phi. Empezando con 0 y 1, cada número de la serie es simplemente la suma de los dos anteriores. Así: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .
La razón (proporción) de cada par sucesivo de números en la serie se aproxima a phi (1.618. . .). Así si dividimos 5 entre 3 es 1.666..., y 8 entre 5 es 1.60. En la medida en la que vamos mas lejos del 0 (punto de inicio de la secuencia) nos acercamos al valor de phi.
La tabla de abajo nos muestra como las proporciones de números sucesivos en la serie Fibonacci se aproxima a Phi.
Puedes computar cualquier número de la serie Fibonacci fácilmente. Usa phi para saber cualquier numero (n) de la serie Fibonacci (f)
fn = Fn / 5½
Phi puede derivarse matemáticamente resolviendo la ecuación:
n2 - n1 - n0 = 0 que es lo mismo que n2 - n - 1 = 0
Esta ecuación la rescribimos y nos queda así:
n2 = n + 1 y 1 / n = n - 1
La solución a la ecuación es la raíz cuadrada de 5 más 1 dividido entre 2
( 5½ + 1 ) / 2 = 1.6180339... = F
Esto resulta en dos propiedades únicas de phi:
Si elevas al cuadrado a phi, obtienes un numero exactamente 1 mayor que phi: 2.6180...
F2 = F + 1
Si divides a phi entre 1, obtienes un numero exactamente a 1 menos phi: 0.6180...:
1 / F = F - 1
Phi, curiosamente, puede ser expresado en cinco: 5 ^ .5 * .5 + .5 = F
Puedes usar phi para computar un número n en la serie Fibonacci (fn): fn = Fn / 5½
Como por ejemplo, el número 40 de la serie Fibonacci es 102, 334, 155, que puede expresarse
f40 = F40 / 5½ = 102,334,155
Este método en realidad nos provee un estimado que siempre esta cerca del numero correcto Fibonacci.
http://www.iuca.net/gs/que%20es%20phi.htm
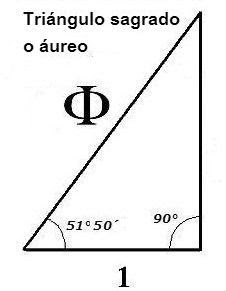
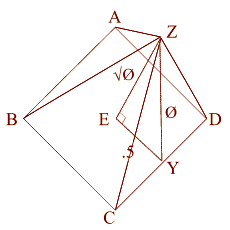









¿Qué es phi?
Phi y la serie de Fibonacci
Funciones trigonométricas
Razones matemáticas
Pentágono
Espirales Áureas
Inicio :: Ver temas relacionados: Decalogo Geometria Sagrada :: Número de Oro :: Merkaba
¿Qué es phi?
Phi (1.618033988749895... ), pronunciado como fi, es un numero irracional como Pi ( 3.14159265358979... ), pero con muchas características matemáticas inusuales. Phi es la base de la Proporción Dorada. La razón o proporción determinada por Phi (1.618...) era conocida por los Griegos como la “Sección Dorada” y por los artistas del renacimiento como la “Proporción Divina”. También se le conoce como la razón Dorada o la Proporción Áurea.
Phi, como Pi, es una razón definida por una construcción geométrica.
Pi es la relación de la circunferencia de un círculo respecto a su diámetro. Phi es la proporción de los segmentos de una línea que resultan cuando una línea es dividida de una forma única y especial.
La línea es dividida para que la proporción de la longitud de la línea entera (A) respecto a la longitud del segmento de la línea mayor (B) sea igual que la proporción de la longitud del segmento de la línea mayor (B) a la longitud del segmento de la línea menor (C)

Esto es que A es 1.618... veces B, y B es 1.618… veces C. Recíprocamente, C es 0.618... de B y B es 0.618... de A. Phi con mayúscula "Phi" es 1.6180339887..., mientras que phi con minúscula es 0.6180339887, el reciproco de Phi o Phi menos 1.
Lo que hace a phi incluso mas inusual es que puede derivarse de muchas formas y ser encontrado en proporcionalmente en el universo. Phi F puede ser derivado por: la serie numérica descubierta por Leonardo Fibonacci, matemáticas y geometría.
Phi y la serie de Fibonacci
Leonardo Fibonacci, por herencia del mundo árabe, descubrió la serie que nos lleva a phi. En el siglo XII, Leonardo Fibonacci descubrió una serie numérica simple que es la base de la increíble relación que encontramos detrás de phi. Empezando con 0 y 1, cada número de la serie es simplemente la suma de los dos anteriores. Así: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .
La razón (proporción) de cada par sucesivo de números en la serie se aproxima a phi (1.618. . .). Así si dividimos 5 entre 3 es 1.666..., y 8 entre 5 es 1.60. En la medida en la que vamos mas lejos del 0 (punto de inicio de la secuencia) nos acercamos al valor de phi.
La tabla de abajo nos muestra como las proporciones de números sucesivos en la serie Fibonacci se aproxima a Phi.
Puedes computar cualquier número de la serie Fibonacci fácilmente. Usa phi para saber cualquier numero (n) de la serie Fibonacci (f)
fn = Fn / 5½
Phi puede derivarse matemáticamente resolviendo la ecuación:
n2 - n1 - n0 = 0 que es lo mismo que n2 - n - 1 = 0
Esta ecuación la rescribimos y nos queda así:
n2 = n + 1 y 1 / n = n - 1
La solución a la ecuación es la raíz cuadrada de 5 más 1 dividido entre 2
( 5½ + 1 ) / 2 = 1.6180339... = F
Esto resulta en dos propiedades únicas de phi:
Si elevas al cuadrado a phi, obtienes un numero exactamente 1 mayor que phi: 2.6180...
F2 = F + 1
Si divides a phi entre 1, obtienes un numero exactamente a 1 menos phi: 0.6180...:
1 / F = F - 1
Phi, curiosamente, puede ser expresado en cinco: 5 ^ .5 * .5 + .5 = F
Puedes usar phi para computar un número n en la serie Fibonacci (fn): fn = Fn / 5½
Como por ejemplo, el número 40 de la serie Fibonacci es 102, 334, 155, que puede expresarse
f40 = F40 / 5½ = 102,334,155
Este método en realidad nos provee un estimado que siempre esta cerca del numero correcto Fibonacci.
http://www.iuca.net/gs/que%20es%20phi.htm





|
|
|
|
|
Cartago - Tanit Tanit - Wikipedia, la enciclopedia libreTanit fue la diosa más importante de la mitología cartaginesa, la consorte de Baal y patrona de Cartago. Era equivalente a la diosa fenicia Astarté; también fue una deidad bereber. Fue la diosa de Ibiza (Islas Baleares, España). [editar]Culto El culto a Tanit comenzó a cobrar importancia a partir del siglo V a. C., y estaba asociado con la Luna y la fertilidad. Hay indicios de que iba acompañado de ritos con sacrificio de niños, pero esta creencia pudiera ser fruto de la política de descrédito romana, A partir del siglo V a. C., Tanit se convierte en la diosa principal del panteón de Cartago, sustituyendo a su predecesora. En la epigrafía a menudo aparece denominada Tnt pn B’l (Tanit faz de Baal), siendo, pues, una manifestación, o incluso la divinidad paredra, del dios Baal, aunque con el tiempo acabará apareciendo sola en las inscripciones. A partir del 400 a. C., su culto está documentado en muchos lugares mediterráneos: Sidón en el Líbano; Kition en Chipre; Thinissut, Hadrumentum y Constantina en el Norte de África; Tharros, Sulcis y Nora en Cerdeña; Tossal de la Cala en Benidorm y Lilibeo y Palermo en Sicilia. Su grafía en púnico es Tnt, dado que las lenguas semitas se escriben sin vocales. Pero, a pesar de que su nombre aparece escrito como Tanit, su pronunciación verdadera, al menos en época tardía, sería aproximadamente Tinit.e Su símbolo era una circunferencia sobre un trazo horizontal y un triángulo o "V" invertida. Inicialmente, el triángulo era un trapecio. Algunos estudiosos lo asocian con el símbolo Anj del Antiguo Egipto. En el Sur de la Península Ibérica, en la desembocadura del río Guadalhorce, apareció un poblado fenicio y entre sus enseres y ajuares una Tanit en bastante buen estado de conservación. [editar]Enlaces externos  Click para ampliar  Luna de Lunes en U  Click para ampliar   Arriba: restos del altar de Tanit en el tophet de Cartago, donde se realizaron sacrificios infantiles a lo largo de al menos 1.000 años, desde su fundación hasta su conquista por los romanos. Se cree que en el momento de la conquista esta práctica se había degradado y contaminado en gran medida. En el altar, aún puede distinguirse el signo de Tanit. Yacimiento arqueológico de Cartago, actualmente en Túnez.  Baal - Bell - Bull - toro  Click para ampliar  Pelicula Dali - Disney  Tanit cara de Leon - Juda - puertas de Leo  Tinker-Bell significa campana reparadora - codigo regenerativo  Puertas de Europa - Tanit - simbolo del luto CARTAGO_SIGNO_DE_TANITMensajes subliminales en esta web de la Dra Maria Vazquez Hoys Vade retro satana - Wikipedia, la enciclopedia libre Click para ampliar    Uvas - fermentacion a la izquierda y la granada - rombo dodecaedro a la derecha  Tanit junto a su consorte el Toro Baal y el 8 095 Iniciado por Gabi  Entonces el triángulo invertido con la luna encima sería igual a la cabeza del toro. Baal?
La campana sería parecido, el triángulo invertido con la línea encima y un circulo pequeño. Tanit?
Salud
Como siempre los codigos pueden ser ambiguos, pero basicamente el mensaje es el triangulo equilatero con la granada y las uvas saliendo de los cuernos de la abundancia, el mana de cristo, la nueva vida. La campana es la llave de la vida sobre el mismo triangulo, que posiblemente en la ambiguedad del codigo pase a ser el cono orbital ya que en muchos casos no tiene 60 grados, tambien puede representar el espiral aureo sobre los 72 grados - 360/5, o sea el codigo de la Diosa Venus - Tanit en este caso. El circulo seguramente sea Venus, la estrella de 5 puntas que vemos en la bandera por ejemplo de Mauritania.  Click para ampliar  Pero puede que tambien represente el regreso a la orbita circular, el tiempo lento original de la era Saturniana dorada, el hipercubo octogonal, recordemos a mayor velocidad mayor excentricidad, la velocidad es un reflejo del espiral central de la galaxia, al comienzo se mueve mas lento y a medida que el espiral se va achicando la velocidad aumenta tal como pasa con la orbita de Mercurio el mensajero veloz de los Dioses del fuego.  Click para ampliar  Despues viene el Orden del Caos junto a las aguilas y el huevo cosmico humpty dumpty Pero el Caos tiene una distribucio matematica que es la campana deGauss  Donde econtramos esta formacion ?  Click para ampliar  Por ejemplo en el medio del escudo de la familia Rothschild flanqueado por el unicornio simbolo de singularidad.  http://en.wikipedia.org/wiki/Gaussian_******** http://en.wikipedia.org/wiki/Gaussian_********Aplicaciones Funciones gaussianas aparecen en muchos contextos de las ciencias naturales , las ciencias sociales , las matemáticas y de ingeniería . Algunos ejemplos incluyen: En las estadísticas y teoría de la probabilidad , las funciones gaussianas aparecen como la función de densidad de la distribución normal , que es una limitación de distribución de probabilidad de sumas complicadas, según el teorema del límite central . Funciones gaussianas son la función de Green para el (homogénea e isotrópica) la ecuación de difusión (y, lo que es lo mismo, a la ecuación del calor ), una ecuación diferencial parcial que describe la evolución temporal de una masa de densidad en la difusión . En concreto, si la densidad de masa en el momento t = 0 está dado por una delta de Dirac , que en esencia significa que la masa se concentró en un solo punto, entonces la masa de distribución en el tiempo t vendrá dado por una función de Gauss, con el parámetro un ser linealmente relacionada con 1 / √ t y c ser linealmente relacionada con √ t . Más generalmente, si la masa inicial de densidad es φ ( x ), entonces la densidad de masa en los últimos tiempos se obtiene tomando la convolución de φ con una función de Gauss. La convolución de una función con una gaussiana también se conoce como un Weierstrass transformar . Una función gaussiana es la función de onda del estado fundamental del oscilador armónico cuántico . Los orbitales moleculares se utilizan en química computacional pueden ser combinaciones lineales de funciones gaussianas llamados orbitales gaussianos (véase también el conjunto de base (química) ). Matemáticamente, los derivados de la función de Gauss se puede representar mediante funciones de Hermite . La n -ésima derivada de la gaussiana es la función de Gauss se multiplicó por el n -ésimo polinomio de Hermite , hasta la escala. Por ejemplo, la primera derivada de la gaussiana es simplemente la de Gauss multiplicado por x . En consecuencia, las funciones gaussianas se asocia también con el estado de vacío en la teoría cuántica de campos . Vigas gaussianas se utilizan en los sistemas ópticos y de microondas. En el espacio escala de representación, las funciones gaussianas se utilizan como suavizar los granos para la generación de multi-escala representaciones en visión por computador y procesamiento de imágenes . Específicamente, los derivados de gaussianas ( funciones de Hermite ) se utilizan como una base para definir un gran número de tipos de operaciones visuales. Funciones gaussianas se utilizan para definir algunos tipos de redes neuronales artificiales . En la microscopía de fluorescencia una función gaussiana 2D se utiliza para aproximar el disco de Airy , que describe la distribución de la intensidad producida por una fuente puntual . En el procesamiento de señales que sirven para definir filtros Gaussianos , como en el procesamiento de imágenes donde gaussianas 2D se utilizan para desenfoques Gaussianos . En el procesamiento de señales digitales , una utiliza un discreto núcleo gaussiano , que puede ser definida mediante el muestreo de una gaussiana, o de una manera diferente. En geoestadística se han utilizado para la comprensión de la variabilidad entre los patrones de un complejo de la imagen de formación . Se utilizan los métodos del kernel para agrupar los patrones en el espacio de características. [ 5 ] http://www.forocoches.com/foro/showthread.php?t=2694602&page=5 |
|
|
 Primer Primer
 Anterior
39 a 53 de 203
Siguiente Anterior
39 a 53 de 203
Siguiente Último
Último
|


En Argentina, la noticia del nacimiento real quedó eclipsada por la visita del Papa Francisco a Río de Janeiro, informó el corresponsal de BBC Mundo en Buenos Aires, Ignacio de los Reyes.
"Aunque el bebé de los duques de Cambridge fue tema en tertulias de radio y televisión, los argentinos y los medios nacionales parecen mucho más interesados en la llegada del compatriota Jorge Bergoglio a Latinoamérica y en el nombramiento del rosarino Gerardo 'Tata' Martino como nuevo director técnico del FC Barcelona", informó el corresponsal.