Dodecaedro

De Wikipedia, la enciclopedia libre

Dodecaedro regular
Familia: Sólidos platónicos
Imágen del sólido
Caras	12
Polígonos que forman las caras	Pentágonos regulares
Aristas	30
Vértices	20
Grupo de simetría	Icosaédrico (I_h)
Poliedro dual	Icosaedro

Un dodecaedro (del griego δώδεκα, ‘doce’ y ἕδρα; ‘asiento’, ‘posición’, en geometría ‘cara’) es un poliedro de doce caras, convexo o cóncavo. Sus caras han de ser polígonos de once lados o menos. Si las doce caras del dodecaedro son pentágonos regulares, iguales entre sí, el dodecaedro es convexo y se denomina regular, siendo entonces uno de los llamados sólidos platónicos.

Recientes investigaciones científicas han propuesto que el espacio dodecahédrico de Poincaré sería la forma del Universo^[1] ^[2] ^[3] y en el año 2008 se estimó la orientación óptima del modelo en el cielo.^[4]

Contenido

[ocultar]

[editar] Dodecaedro regular

Plantilla para armar un dodecaedro regular.

[editar] Cálculo de dimensiones fundamentales

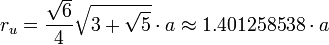
Radio externo: $r_u=frac{sqrt{6}}{4} sqrt{3 +sqrt{5}} cdot a approx 1.401258538 cdot a$
Radio interno: $r_i=frac{a}{4} sqrt{ frac{50+22sqrt{5}}{5} } approx 1.113516364 cdot a$

En todo poliedro regular, el número de caras más el número de vértices, es igual al número de aristas más 2.

$C + V = A + 2 ,$

donde: C = número de caras; V = número de vértices; A = número de aristas

[editar] Área

Animación de uno de los desarrollos del Dodecaedro.

El área total de sus caras, A (que es 12 veces el área de una de ellas, A_c) es igual a:

$A = 12 cdot frac{sqrt{25+10 sqrt{5}}}{4} cdot a^2 = 3 sqrt{25+10 sqrt{5}} cdot a^2 approx 20,65cdot a^2$

También se puede con esta fórmula basada en parte en la trigonometría:

$A = frac{15 l^2}{tan 36^o}$

[editar] Volumen

Para un dodecaedro de arista A, se puede calcular su volumen V mediante la siguiente fórmula:

$V = frac{1}{4} left(15+7 sqrt{5} ight)cdot a^3 approx 7,66 cdot a^3$

[editar] Ángulos diedros

Los ángulos entre cada par de caras son:

$alpha = 180 - arccos left( an{18} imes an{54} ight) = 116,57^o$

[editar] Propiedades particulares

[editar] Simetría

Dado de un juego de rol en forma de dodecaedro.

Un dodecaedro regular tiene seis ejes de simetría de orden cinco, las rectas que unen los centros de caras opuestas; quince ejes de simetría de orden dos, las rectas que unen los centros de aristas opuestas; quince planos de simetría, que contienen cada pareja de aristas opuestas coplanares; y un centro de simetría. Esto hace que este cuerpo tenga un orden de simetría total de 120: 2x(6x5+15x2).

Los elementos de simetría anteriores definen uno de los grupos de simetría icosaédricos, el denominado I_h según la notación de Schöenflies.

El dodecaedro tiene también diez ejes de simetría de orden tres: las rectas que unen cada par de vértices opuestos. Subdividiendo cada cara del dodecaedro en triángulos se pueden construir domos geodésicos.

[editar] Aplicaciones y ejemplos

En los juegos de rol el dado de doce caras es un dodecaedro regular. Su notación escrita es «D12».

http://es.wikipedia.org/wiki/Dodecaedro

Metatron's Cube

After showing that the A-shaped Tree of Life relates to Metatron's Cube, and how both the tree and cube map to the dodecahedron and the DC map, the intention here is to present a mental exercise where we imagine the DC ladscape overlaid on to a stellated dodecahedron, just like the tree and cube.

This image from earlier shows how the dodecahedron relates to a 3D depiction of a cube, and how the Tree of Life maps to points on the dodecahedron. It also illustrates how the 13 circles in Metatron's Cube relate to the corner and faces of the dodecahedron. Three of the outer circles map to faces that we can see, three others to faces turned slightly away from us.

Three of the inner circles map to the three faces on this side, while the other three correlate to three faces (turned upside down) on the opposite side. These last three are all marked by features in the map relating to G Washington; Washington Circle, Mt Vernon Square and the Wash Mmt (5,4 and 9).

The image below is what's called a stellated dodecahedron, where the points in the centers of the faces are raised so that a straight line connects them. Compare this figure with the grey Metatron's Cube above. This image results from bringing 5 equilateral triangles together at a point.

Notice how when the edges of the pentagons meet, 2 of these equilateral triangles form a flat plane, and the line between the new middles of the faces (in blue below) bisects the line formed where two faces meet, creating the same rhombus figure that is generated by the vesica. 5 of these rhombus figures meet at the center of each pentagon here. Just as elsewhere, three of these rhombus depict a 3D cube (in blue above).

This image shows the overlapping pentagon and hexagon/cube on both the map and deodecahedron. These account for 9 of the eleven points in the tree figure.

The Wash Mmt is at the bottom of the hexagon

The WH, which is at the corner of the dodeachedron, is at the bottom of the pentagon

Scott Circle is at the top of the hexagon, in the middle of a pentagonal face

Wash Cr, MtV Sq, and the WM (all affiliated with GW) all lie at points where 3 faces meet (at corners of pentagons).

The triangle at the top of the map figure is one of the five triangles making up a stellated face, so the top is at the center of a face.

The Jefferson Memorial, at the bottom of the tree, falls on the center of a face

The other two corners of the hexagon, the Archives Bldg and the Med Ctr, both lie in the middle of a face, like Scott Cr (accounting for 5 of 12 faces, so far).
The illusion of the hex/cube derives from a series of lines that connect a pentagon corner to a center, then that center to another corner, and to another center, etc. Rememeber that the CB and Jeff Mml are located north of where they should be.

The sides of a dodecahedron come together in threes just like a cube does, but it forms a different solid since it has different angles and number of sides on it's faces. When you view these next images, remember that we are attempting to lay the map on a dodecahedron like a rubber sheet. Note what was said before about finding the corners of pentagons by extending the sides of hexagons.

As you can see, extending P and NY Aves (in purple) indicate the directions to 4 other centers of faces (peaks on the dodecahedron). These are the corners of the Big Rectangle in Metatron's Cube. NY, Penn Ave and 16th Street mark the x, y and z axis in the cube map. Two of the corners are marked by the CB and Georgetown, at opposite ends of PA.

The position of the NE corner is determined by running a line north of the CB, and extending NY Avenue. These meet in the same place where N Street (which runs through the middle of Scott Circle) crosses there. Running west, N Street marks the NW corner where it crosses PA in G'town. The southwest corner can be found by extending NYA to the SW, but no landmark exists there.

The centers of four faces correlate to the four corners above, three more to the front faces in red, and two more the point at the top and the Jeff Mml at the bottom of the tree; that's nine of the 12 faces. The red circles correlate to the centers of three faces on the opposite side of the dodecahedron. I suspect that extension of PA past the Capitol and the section of DC east of the CB, wraps around the figure, but I have not worked that out yet.

DC Symbols Homepage