|
Réponse |
Message 1 de 115 de ce thème |
|
|
|
|
|
Réponse |
Message 71 de 115 de ce thème |
|
|
|
|
Réponse |
Message 72 de 115 de ce thème |
|
|
|
|
Réponse |
Message 73 de 115 de ce thème |
|
|
|
|
Réponse |
Message 74 de 115 de ce thème |
|
|
|
|
Réponse |
Message 75 de 115 de ce thème |
|
|
|
|
Réponse |
Message 76 de 115 de ce thème |
|
| Reply |
Message 5 of 6 on the subject |
|
|
|
|
| Reply |
Message 6 of 6 on the subject |
|
The Language of the Divine Architect
The creation myths of many traditions describe the universe as the work of a Divine Architect who uses “sacred geometry” to unfold the dimensions of a beautiful cosmos, wisely designing every aspect of it, and governing by just proportions evidenced in the geometric shapes and processes of nature.
   
The language of God is mathematical language of numbers, proportions and (sacred) geometry.
“As Above, So Below” – these words circulate throughout occult and magical circles, and they come from Hermetic texts. The concept was first laid out in The Emerald Tablet of Hermes Trismegistus, in the words “That which is Below corresponds to that which is Above, and that which is Above, corresponds to that which is Below, to accomplish the miracles of the One Thing”
The entire Universe (including our solar system, as well as atoms, DNA and life-forms) reveals the secrets of balance, rhythm, proportion and unity in diversity, the fractal interconnection of parts with each other and the whole. This harmony is expressed by some “key” numbers: Fibonacci Series, Phi, Pi and “e”.
The first 21 Fibonacci numbers:
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765

A simple number pattern, known as the Fibonacci Series, sits at the heart of the marvelous architecture and patterns of life and growth.
These few equations are the “seeds” of God’s “Grand Design” ( God’s “fingerprint”):
Pi = (6/5) * phi2
Euler’s Identity Equation:

where
e – is Euler’s number, the base of natural logarithms
i – is the imaginary unit, which satisfies i2 = sqrt(-1)
Pi – is the ratio of the circumference of a circle to its diameter
phi- is the the golden ratio number 1.618034
Mathematical beauty of Euler’s Identity
Euler’s identity is considered by many to be remarkable for its mathematical beauty. These three basic arithmetic operations occur exactly once each: addition, multiplication, and exponentiation. The identity also links five fundamental mathematical constants:
The number 0, the additive identity.
The number 1, the multiplicative identity.
The number Pi, which is ubiquitous in trigonometry, the geometry of Euclidean space, and analytical mathematics (Pi = 3.14159265…)
The number e, the base of natural logarithms, which occurs widely in mathematical and scientific analysis (e = 2.718281828…). Both “pi” and “e” are transcendental numbers.
The number i, the imaginary unit of the complex numbers, a field of numbers that contains the roots of all polynomials (that are not constants), and whose study leads to deeper insights into many areas of algebra and calculus, such as integration in calculus.
Furthermore, in algebra and other areas of mathematics, equations are commonly written with zero on one side of the equals sign.
A poll of readers conducted by The Mathematical Intelligencer magazine named Euler’s identity as the “most beautiful theorem in mathematics”. Another poll of readers that was conducted by Physics World magazine, in 2004, chose Euler’s identity tied with Maxwell’s equations (of electromagnetism) as the “greatest equation ever” — Wikipedia

A simple number pattern, known as the Fibonacci Series, sits at the heart of the marvelous architecture and patterns of life and growth.
Pi and phi
Pi = (6/5) * phi2
300 * Pi = 360 * phi2
For a circle with radius = 1 we get this equation for
(close approximation of) its circumference:
2 * Pi = (360/150) * phi2
There is another way to write this equation:
Pi – Phi2 = 0.2 * phi2
Lets calculate the value:
Pi – phi2 = 0.5236
this number in meters is equal 20.614 inches = 1 Royal Egyptian Cubit
(unit of length used by ancient Egyptians during construction of pyramids)
3:6:9
“If you only knew the magnificence of the 3, 6 and 9, then you would have a key to the universe.” –-N.Tesla
Perhaps Tesla had in mind another thing altogether. It basically boiled down to energy/field/consciousness, which equates in to electricity/magnetism/consciousness, that made up Trinity. Energy is your divine spark, and field is the area you exist within. The 2 things that allow consciousness to isolate itself is electricity and magnetism. NOTHING in the physical universe exists outside energy and field…only then can you have consciousness reside inside a material existence.
3:6:9 … Perhaps these numbers were intentionally expressed by the pyramids of Giza…? There are 9 pyramids on the Giza plateau: 3 large pyramids and 6 small “satellite” pyramids. Also, the design of the Second (Khafre) Pyramid of Giza is based on ratio 9:6.
Note: 6:5 is another special ratio used in ancient times
The Fibonacci series has a pattern that repeats every 24 numbers
Numeric reduction is a technique used in analysis of numbers in which all the digits of a number are added together until only one digit remains. As an example, the numeric reduction of 256 is 4 because 2+5+6=13 and 1+3=4. Applying numeric reduction to the Fibonacci series produces an infinite series of 24 repeating digits:
1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9
If you take the first 12 digits and add them to the second twelve digits and apply numeric reduction to the result, you find that they all have a value of 9.
1st 12 numbers: 1 1 2 3 5 8 4 3 7 1 8 9
2nd 12 numbers: 8 8 7 6 4 1 5 6 2 8 1 9
Numeric reduction – Add rows 1 and 2: 9 9 9 9 9 9 9 9 9 9 9 18
Final numeric reduction – Add digits of result: 9 9 9 9 9 9 9 9 9 9 9 9
|
|
|
|
|
|
Réponse |
Message 77 de 115 de ce thème |
|
| Reply |
Message 89 of 90 on the subject |
|
|
|
|
| Reply |
Message 90 of 90 on the subject |
|
|
|
|
|
|
|
Réponse |
Message 78 de 115 de ce thème |
|
 
1. Génesis 28:12 Y soñó: y he aquí una ESCALERA que estaba apoyada en tierra, y su extremo tocaba en el cielo; y he aquí ángeles de Dios que subían y descendían por ella.
2. 1 Reyes 6:8 La puerta del aposento de en medio estaba al lado derecho de la casa; y se subía por una ESCALERA de caracol al de en medio, y del aposento de en medio al tercero.
 
LA TORRE DE BABEL, OSEA LA UNION ENTRE EL CIELO Y LA TIERRA, ES UN "AGUJERO DE GUSANO". EN ESTE MARCO ES EL GRIAL MISMO. SIMBOLIZA LA UNION ENTRE EL CIELO Y LA TIERRA, O LA CUADRATURA DEL CIRCULO (CIRCULO=CIELO; CUADRADO=TIERRA) O LA ESCUADRA Y EL COMPAS MASONICO. ES OBVIA LA CONNOTACION CON LA "ESCALERA DE JACOB". MAGDALENA TIENE CONNOTACION CON EL MISMO TERMINO TORRE EN HEBREO.
1. Josué 15:37 Zenán, HADASA, Migdal-gad,
2. Ester 2:7 Y había criado a HADASA, es decir, Ester, hija de su tío, porque era húerfana; y la joven era de hermosa figura y de buen parecer. Cuando su padre y su madre murieron, Mardoqueo la adoptó como hija suya.
ESTHER=ISHTAR=STAR GATE=PUERTA ESTELAR
BABEL=PUERTA DE DIOS

ESCUADRA Y COMPAS MASONICO=CUADRADO / CIRCULO
1 Pedro 5:13: La iglesia que está en Babilonia, elegida juntamente con vosotros, y Marcos mi HIJO, os saludan.
HECHOS 12:12 / 33 / JUAN MARCOS
ESTRELLA DE 6 PUNTAS = 33 = 2 TRIANGULOS CRUZADOS =ALQUIMIA
3. Ezequiel 41:7 Y había mayor anchura en las cámaras de más arriba; la ESCALERA de caracol de la casa subía muy alto alrededor por dentro de la casa; por tanto, la casa tenía más anchura arriba. Del piso inferior se podía subir al de en medio, y de éste al superior.
| Reply |
Message 89 of 90 on the subject |
|
|
|
|
| Reply |
Message 90 of 90 on the subject |
|
|
|

| milky way in Simple Gematria Equals: 119 |
( |
m 13 |
i9 |
l 12 |
k 11 |
y 25 |
0 |
w 23 |
a1 |
y 25 |
) |
| queen mary in Simple Gematria Equals: 119 |
( |
q 17 |
u 21 |
e5 |
e5 |
n 14 |
0 |
m 13 |
a1 |
r 18 |
y 25 |
|
| hebrew calendar in Simple Gematria Equals: 119 |
( |
h8 |
e5 |
b2 |
r 18 |
e5 |
w 23 |
0 |
c3 |
a1 |
l 12 |
e5 |
n 14 |
d4 |
a1 |
r 18 |
| mary magdalene in Simple Gematria Equals: 119 |
( |
m 13 |
a1 |
r 18 |
y 25 |
0 |
m 13 |
a1 |
g7 |
d4 |
a1 |
l 12 |
e5 |
n 14 |
e5 |
|

|
|
|
|
Réponse |
Message 79 de 115 de ce thème |
|
|
|
|
Réponse |
Message 80 de 115 de ce thème |
|
Are Singularities Real?
It’s hard to imagine infinity: something that is, by definition, larger than everything you can imagine. Physicists have to deal with the unimaginable every day, and have the tools to do so. But does their math describe reality?
Mathematicians have found a way to pack infinity into manageable equations and theorems as part of a class of mathematical oddities called “singularities.” To a mathematician, a singularity is simply a point where a function breaks down, as 1/x does when x gets close to zero. The defining property of a singular point is that it’s impossible to predict what happens beyond it. But are the singularities in mathematicians’ equations just an abstract concept? Or do they occur in nature?
 The word “singularity” was popularized in a 2005 book by Ray Kurzweil, who uses it to refer to an impending revolution in artificial intelligence (AI). According to Kurzweil, once artificial intelligences become smart enough to improve their own kin, a feedback loop will lead to a runaway process. After that, all bets are off: nobody knows what will happen. But Kurzweil’s technological singularity, if it comes to pass, is not a true singularity. There is no law of nature that limits our ability to predict what might happen once AI evolves past the “singularity” point; we’re confined instead by the limits of the human mind.
Though they sound exotic, mathematical singularities are actually common in solutions to all but the simplest equations in physics. The formation of shock waves and cracks, and even the motion of a billiard ball bouncing off a hard wall, can contain singularities. While these singularities fulfill the mathematical definition, they aren’t physically real either: they arise from idealized assumptions that physicists make to force the messy world of reality into the neat one of mathematics. In reality, no crack is perfectly sharp, no wall is perfectly hard, no shock wave is perfectly localized.
Here is another example: Turn down the water on your kitchen tap until it starts dripping. The hydrodynamical equation describing the surface of the drops has a singularity at the pinching point: you cannot from one drop predict where the next will be. But this singularity, too, can be avoided by applying a more suitable theory. Using atomic physics, you could, in principle, calculate exactly how the water stream breaks apart on the level of single atoms. All these singularities are thus artifacts of using a theory outside its range of applicability, on distances so short that a more precise theory would be needed.
The one type of singularity that might be real—that physicists don’t know how to resolve—is the one that appears in Einstein’s theory of General Relativity when matter collapses under the gravitational pull of its own weight. There is nothing in General Relativity that then stands in the way of this collapse. It will continue until all the matter is located at a single point of infinite matter density and infinite space-time curvature: a singularity.
The singularities that appear inside black holes pose a big problem for physicists. Crossing a black hole’s event horizon is like jumping into a river upstream of a waterfall, at a place where the water flows faster than you can swim. Whatever you do, you’ll end up being pulled down the waterfall. Likewise, whatever falls into a black hole is pulled down into the singularity. And once there, it reaches its end.
At the black hole singularity every particle’s path seems to dead-end. Space-time stops at the singularity, and nobody knows what happens at this point. Yet we cannot imagine how something can just end. The black hole space-time is for this reason referred to as “incomplete,” but in General Relativity there is no way to complete it. This is the origin of the black hole information loss problem: It is the horizon that makes the information irretrievable, but it is the singularity that ultimately annihilates it. This is a big headache for physicists because such annihilation of information is incompatible with quantum mechanics.
The Big Bang is a singularity, too. If you run the expansion of the universe which we observe today backwards, then the density of matter must have been larger the younger the universe was, all the way back to an initial moment where the density must have been infinitely high: it must have been singular.
Are these singularities real, or just vestiges of the gap between math and reality? Based on their experience with other systems, physicists suspect that the singularities in General Relativity are a warning, a tip-off that we need another theory to describe the physics in the extreme situations when gravity is very strong and its quantum effects are very large. Physicists still don’t know how to describe the quantum effects of gravity, but we hope that by doing so we will one day resolve the singularities.
None of our measuring devices can show an infinite value. Not only have we never observed it, we don’t know how to observe it—we don’t know how to even give meaning to such an observation. Physicists therefore treat singularities as symptoms of an ill theory in need of a cure. It would be possible to mathematically deal with the singularities. But based on past experience and intuition, for all we know so far, nature doesn’t like sudden ends. Does nature make an exception for black holes? Right now, we just don’t know.
Go Deeper
Author and editor’s picks for further reading
Ask a Physicist: What are singularities? Do they exist in nature?
An accessible explanation of singularities in math and physics, from water whirlpools to black holes.
arXiv: Singularity Theorems in General Relativity: Achievements and Open Questions
In this technical paper, theoretical physicist José M.M. Senovilla explores how physicists have understood the singularities in Einstein’s theory over the last century.
Inside Science: Black Hole Cores May Not Be Infinitely Dense
A theory of quantum gravity called loop quantum gravity could eliminate the singularities inside black holes and at the moment of the Big Bang.
|
|
|
|
Réponse |
Message 81 de 115 de ce thème |
|
Martin Gardner, puzzle master extraordinaire
 Image copyrightOTHER Image copyrightOTHER
The writer and puzzle master Martin Gardner, who died in 2010, was once said to have turned dozens of innocent youngsters into maths professors - and thousands of maths professors into innocent youngsters. Maths writer Colm Mulcahy looks back at the amazing career of a man who would have been 100 this week.
Let's warm up with three gems from the vaults:
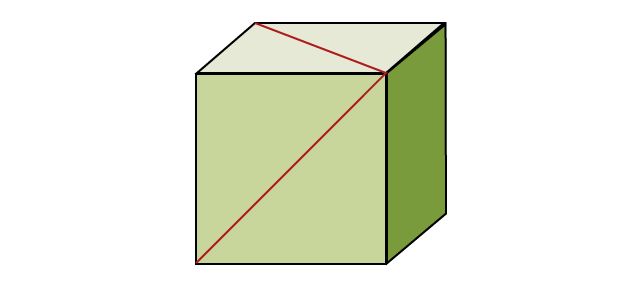
1. What angle is made by the two red lines drawn on the two sides of the cube, as shown in the illustration?
2. A logician visits a distant planet inhabited by two groups of aliens, compulsive liars and faithful truth-tellers. She comes to a fork in a road - one road goes to the left, the other to the right. She meets two aliens there, one a liar, the other a truth-teller... but she doesn't know which is which. The logician must ask just one Yes/No question to discover which road she should take to reach their leader. She thinks for a moment and then asks her question. What question might she have asked?
3. Imagine heating a metal ring enough so it expands. What happens to the hole, does it get bigger or smaller?
 Image copyrightTHINKSTOCK Image copyrightTHINKSTOCK
You may already know the answers to the above questions if you've read some of the 100 or so books written by the American man of letters and numbers, Martin Gardner (1914-2010). His works have long been popular with a variety of people, from science and maths types, to lovers of magic, enemies of pseudoscience, and aficionados of Lewis Carroll - Gardner's Annotated Alice, by far his best seller, has sold more than a million copies.
The most important thing about the three puzzles above is that you can work them out right now, if you have initiative and patience (and a little knowledge of physics). No mathematical training is required. There are some hints at the bottom of the page, and below that, the answers.
Gardner specialised in such puzzles, having studied closely the works of the masters of an earlier generation, England's Henry Dudeney and his American counterpart, Sam Loyd.
The reward for solving puzzles like these, unaided, is to experience priceless Aha! moments. "Googling it is not the Gardner way," says the philosopher Bob Crease in Physics World this month. "The Gardner way is to ignite your fascination so that you experience the pleasure of finding the answer yourself."
Gardner's writing has ignited many sparks over the decades, and even inspired a few scriptwriters fond of nerdy inside jokes. The logician puzzle above resurfaced (slightly repackaged) in the Pyramids of Mars episode of Dr Who, from October 1975. Maths writer Simon Singh, meanwhile, says some of the Simpsons writers - who occasionally slip hidden mathematical references into the storyline - were influenced by Gardner.
One of the last true polymaths, Martin Gardner is best remembered for the quarter century's worth of Mathematical Games columns he wrote for Scientific American magazine, where he injected a spirit of fun and play into a subject many associate with fear and drudgery. It went a lot further than puzzles - there was substance, depth and a fair share of mystery and wonder in the topics he wrote about.
 Image copyrightSCIENCE PHOTO LIBRARYImage captionGardner's column introduced the world to Mandelbrot's fractals Image copyrightSCIENCE PHOTO LIBRARYImage captionGardner's column introduced the world to Mandelbrot's fractals
His lifelong passions included conjuring, chess, wordplay, puzzles of all kinds, science (good, bad and bogus), philosophy and children's literature. He wrote about all of those, extensively, in essays, reviews and books, for a period of 80 years.
http://www.bbc.com/news/magazine-29688355
|
|
|
|
Réponse |
Message 82 de 115 de ce thème |
|
|
|
|
Réponse |
Message 83 de 115 de ce thème |
|
|
|
|
Réponse |
Message 84 de 115 de ce thème |
|
|
|
|
Réponse |
Message 85 de 115 de ce thème |
|

El tunel del tiempo
El asunto del Túnel del tiempo comenzó, en lo que concierne a Harrison, con una serie de acontecimientos tan improbables que parecían una locura, pero que también parecieron inevitables. En un cosmos diseñado para que los seres humanos lo ocuparan, sin embargo debería haber alguna especie de salvaguardia contra las consecuencias de su idiotez. El Túnel del Tiempo pudo ser una de esas salvaguardias. Leinster escribió y publicó más de 1.500 cuentos y artículos durante el transcurso de su carrera. Escribió 14 guiones de películas y centenares de guiones de radio y obras teatrales para televisión, inspirando varias series incluyendo “Tierra de Gigantes” y “El Túnel del Tiempo”. Leinster comenzó a aparecer a finales de los años 1910 en revistas pulp como Argosy y después en Astounding Stories en los años 1930 con regularidad. Se le atribuye la invención de relatos de universos paralelos. Cuatro años antes de que saliera The Legion of Time de Jack Williamson, Leinster escribió su Sidewise in Time. Esta fue la primera vez que el extraño concepto de mundos alternativos apareció en la ciencia ficción moderna.
https://jackmoreno.com/2014/09/15/30-mejores-novelas-de-viajes-en-el-tiempo/ |
|
|
 Premier Premier
 Précédent
71 a 85 de 115
Suivant Précédent
71 a 85 de 115
Suivant Dernier
Dernier
|

