|
Réponse |
Message 1 de 64 de ce thème |
|

Haz clic en la imagen para volver
INICIACIÓN A LOS NÚMEROS DE LA ARQUITECTURA O DE COMO DARLE FORMA A UN EDIFICIO
Los números pueden estar explicados matemáticamente en la “red” pero el problema que plantea el conocimiento de la arquitectura es: ¿cómo se le da forma con esos números a un edificio?. En arquitectura los números operan a partir de los polígonos estrellados formando concatenaciones, tal y como a continuación vamos a describir.

NÚMERO DE ORO - PENTÁGONO
El número de oro viene dado por la solución a la ecuación de segundo grado
x + x² = 1 x = 1+√5 /2 = 1,618033989
Propiedades 1/ 1,618 = 0,618 1,618... x 1,618... = 2,618...
Dado una circunferencia de radio 1 el lado del decágono inscrito en él es 0,618...
Dado un pentágono de lado 1, las diagonales de ese pentágono = 1,618...
La técnica con la que opera la arquitectura es la de las concatenaciones.
Una de ellas, la más usual, es la que presentamos en el dibujo. Si la circunferencia en color azul tiene R=1 el radio de la roja es R= 2,618, correspondiente a la que presentamos en “El vitruvio” de Leonardo da Vinci en la portada de este trabajo.
Se aplicará en la restitución de una tabla de F. Brunelleschi Nº 6.
 
NÚMERO DE PLATA - EL OCTÓGONO
Así como el número de oro está asociado a la √5 el número de plata está asociado a √2 y presenta una serie de propiedades similares a las del número de oro.
√2 = 1,414213562 tg. 22,5º = 0,414213562
tg.67,5º = 2,414213562
1/2,4142... = 0,4142... 2,4142... x 1,4142... = 3,4142...
Observa nuevamente la concatenación, esta vez con el octógono, de la circunferencia en color azul sobre la de color rojo.
Si el radio de la circunferencia azul es 1 la de color rojo es 2,4142....
Si el radio de la circunferencia azul es 0,4142... la de rojo es 1.
Aquí tenéis un ejemplo.
Se aplicará en la Rix House de J. Soane Nº 3.
NÚMERO DE PLATINO - EL HEXÁGONO
De igual forma que el número de oro está relacionado con la √5 y el de plata con la √2, el de platino lo va a estar con la √3
√3 = tg.60º = 1,732050808
1,732... x 2,732... = 4,732...
Combinación, esta, muy utilizada por Andrea Palladio.
Observa la concatenación de la circunferencia azul sobre la de rojo, a través del hexágono, directamente a la circunferencia azul. Si el radio de la circunferencia color azul es 1 el de la circunferencia en color rojo es 2 y el lado del triángulo inscrito es 2 x 1,732...
Este polígono es el más prolífico en la historia de arquitectura como vamos a verlo en los ejercicios.
Aquí tenéis un ejemplo.
Se aplicará al resto de los trabajos Nº 1 - 2 - 4 y 5.
Todos los derechos reservados. Depósito Legal ZA - Nº 69 - 1998
Página web optimizada para ver en resolución de 1024 x 768
2006 - 2007
|
|
|
|
Réponse |
Message 50 de 64 de ce thème |
|
|
|
|
Réponse |
Message 51 de 64 de ce thème |
|
|
|
|
Réponse |
Message 52 de 64 de ce thème |
|
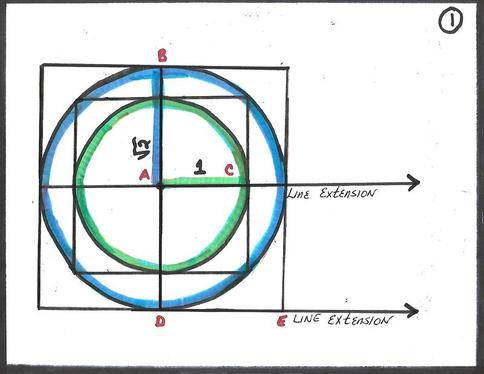
(1) I begin the demonstration with a typical set of nested squares & circles. This diagram is very easy to construct with unmarked compass & straightedge, so I won’t bother with extraneous details. Although measurement is not used to construct these figures, it is obviously required for the proof. Therefore, I will treat the innermost Green Circle as a Unit Circle; (Radius = 1, Area = Pi). The outer Blue Circle is twice the size of the Green Circle; (Radius = √2, Area = 2Pi). Also, you will notice that I’ve labeled key intersecting points with the letters A-E, and made two line extensions; one in the center & one at the bottom. These will come into play in succeeding diagrams.
|
|
|
|
Réponse |
Message 53 de 64 de ce thème |
|
|
|
|
Réponse |
Message 54 de 64 de ce thème |
|
|
|
|
Réponse |
Message 55 de 64 de ce thème |
|
|
|
|
Réponse |
Message 56 de 64 de ce thème |
|
|
|
|
Réponse |
Message 57 de 64 de ce thème |
|
|
|
|
Réponse |
Message 58 de 64 de ce thème |
|
|
|
|
Réponse |
Message 59 de 64 de ce thème |
|
|
|
|
Réponse |
Message 60 de 64 de ce thème |
|
|
|
|
Réponse |
Message 61 de 64 de ce thème |
|
|
|
|
Réponse |
Message 62 de 64 de ce thème |
|
|
|
|
Réponse |
Message 63 de 64 de ce thème |
|
|
|
|
Réponse |
Message 64 de 64 de ce thème |
|
|
|
 Premier Premier
 Précédent
50 a 64 de 64
Suivant Précédent
50 a 64 de 64
Suivant
 Dernier
Dernier

|

