|
|
EL HIPERCUBO, LA CUARTA DIMENSION, EL TIEMPO, LA LEY DE LA RELATIVIDAD DE EINSTEIN Y SU NEXO CON MARCOS 15:33
33. Marcos 15:33: Cuando vino la hora SEXTa, hubo tinieblas sobre toda la tierra hasta la hora novena. (CLAVE MERCURIO-ORION-ISHTAR GATE)

Decimal --- Binario --- Cuaternario
00 -------- 0000 ------ 00
01 -------- 0001 ------ 01
02 -------- 0010 ------ 02
03 -------- 0011 ------ 03
04 -------- 0100 ------ 10
05 -------- 0101 ------ 11
06 -------- 0110 ------ 12
07 -------- 0111 ------ 13
08 -------- 1000 ------ 20
09 -------- 1001 ------ 21
10 -------- 1010 ------ 22
11 -------- 1011 ------ 23
12 -------- 1100 ------ 30
13 -------- 1101 ------ 31
14 -------- 1110 ------ 32
15 -------- 1111 ------ 33
Las Triadas "que nos elevan" como acordes (11, 111, 1111) a través de sus ejes o colúmnas pitagóricas. Los puntos de corte de dos dimensiones.
Aquí el el 3, 7 y 15 decimal, o 3, 13, 33 cuaternario. Puntos, entiendo, de la singularidad en tres planos diferentes. O como fusión de contrarios.
3 veces 3 que nos llevan hasta la eclosión del huevo -singularidad fecundativa-.

3 veces 3 como el PLATO (PI-LATO) de Giza. 3 pirámides grandes, 3 pirámides pequeñas (6) y 9 (3+3+3) en total. 369.
http://www.burbuja.info/inmobiliaria/conspiraciones/297306-hilo-oficial-indigomerovingio-148.html
 |
Click para ampliar |
  Lo que me lleva a relacionar esto del 3 veces 3 con los armónicos solfeggio y sus puntos de corte o frecuencias doradas, donde el "dragón se eleva" Lo que me lleva a relacionar esto del 3 veces 3 con los armónicos solfeggio y sus puntos de corte o frecuencias doradas, donde el "dragón se eleva"
 |
Click para ampliar |
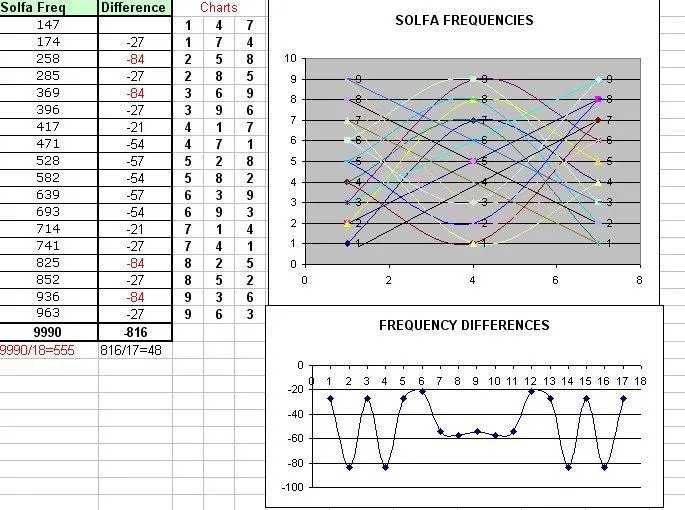 Bettle-Juice, Beetle-Juice, Beetle-Juice.Veo ademas que la suma reducida es 3-6-9. Bettle-Juice, Beetle-Juice, Beetle-Juice.Veo ademas que la suma reducida es 3-6-9.
 |
Click para ampliar |
 3 veces 3. 3 veces 3.
Viene de digitalización de primera semana de curso:
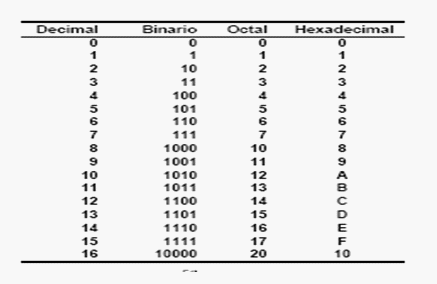
El concepto, que no es nuevo, es que los dieciséis primeros números decimales se pueden mostrar en un nibble binario (medio Byte) resultando 1111 como indicaba IM al representar las coordenadas de los vértices del cubo 4D...
Ahora viene el nuevo apunte...
Que pasa si mostramos esos mismo número decimales en un sistema en base cuatro o cuaternario:
Decimal --- Binario --- Cuaternario
00 -------- 0000 ------ 00
01 -------- 0001 ------ 01
02 -------- 0010 ------ 02
03 -------- 0011 ------ 03
04 -------- 0100 ------ 10
05 -------- 0101 ------ 11
06 -------- 0110 ------ 12
07 -------- 0111 ------ 13
08 -------- 1000 ------ 20
09 -------- 1001 ------ 21
10 -------- 1010 ------ 22
11 -------- 1011 ------ 23
12 -------- 1100 ------ 30
13 -------- 1101 ------ 31
14 -------- 1110 ------ 32
15 -------- 1111 ------ 33
Inquietante... 
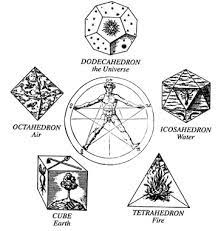
¿Esta letra en base cuatro como se podría representar físicamente? Considero que lo mas adecuado sería un tetraedro regular (formado por 4 triángulos equiláteros), el primero de los sólidos platónicos. Donde cada uno de sus cuatro vértices se encuentran a distancias simétricas entre ellas.
Como para representar el 15 decimal (el 33 en base 4) se necesitan dos dígitos en cuaternario, la forma física de integrar ambas letras sería mediante dos tetraedros unidos en que su vórtices continuaran de forma simétrica.
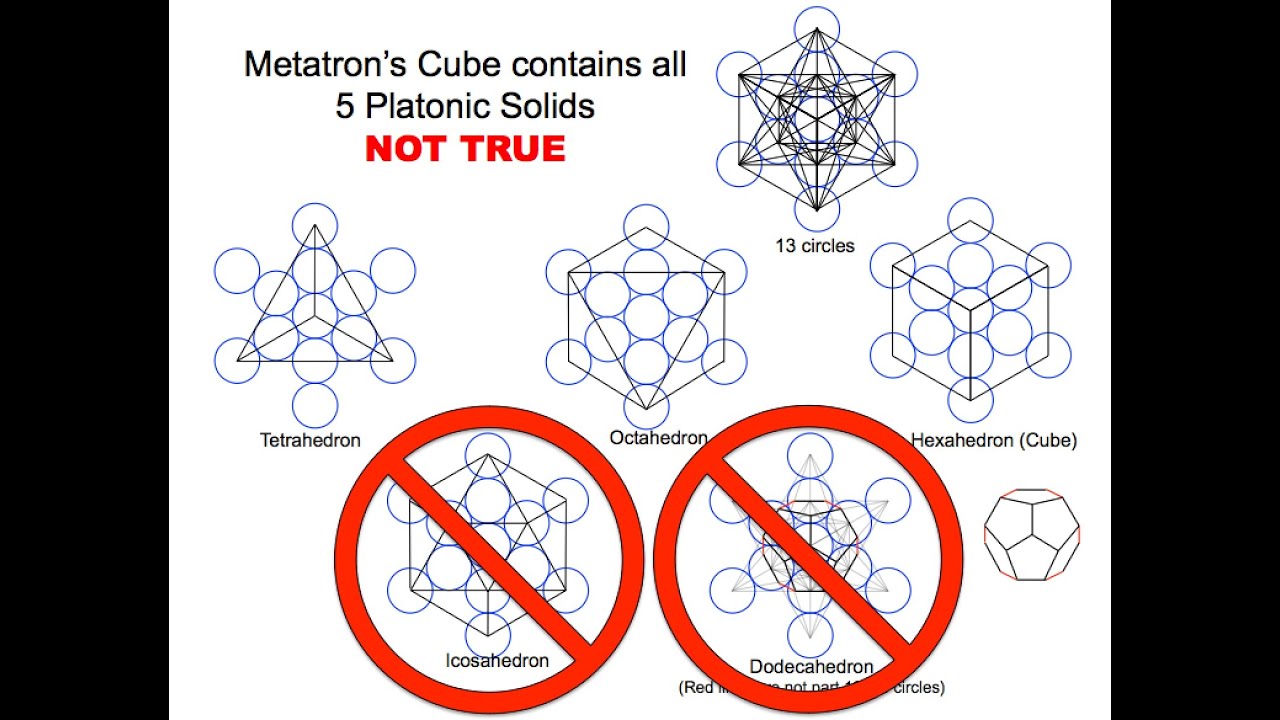
Resumiendo se puede decir, que un hipercubo es lo mismo que lo que se suele representar como Merkaba
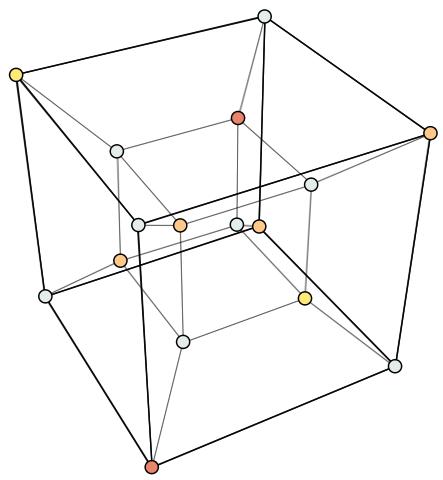


...
..
.
Y que este simbolismo:

Es igual a este:

O al menos que debe representar un concepto muy similar...
|
|
|
|
|


Desde que Leonardo concluyó su célebre pintura en el siglo XV, se han tejido numerosos mitos y leyendas alrededor de esta obra de arte, considerada por los críticos como su “obra más serena y alejada del mundo temporal” y diseñada para poder ser observada en su totalidad y tener una sensación de inmersión. De partida, llama la atención la configuración de sus protagonistas: Jesús ocupa el centro de la escena, y a sus lados existe un equilibrio con seis discípulos a cada lado, agrupados de tres en tres. Los discípulos, según algunos estudiosos, estarían agrupados en “rectángulos”, cuyo significado es unidad y estabilidad. En el centro está Jesús y, al contrario que todos los demás, se encuentra circunscrito en un “triángulo equilátero”, que significa equilibrio perfecto, el triángulo donde reside la majestad y el poder de Dios. El número tres, por lo demás, representa al hombre (cuerpo, mente y espíritu) y a la deidad (Padre, Hijo y Espíritu Santo).

Al fondo del cuadro se puede observar tres ventanales que iluminan la parte central donde está Jesús y donde puede entreverse un paisaje que para algunos simbolizaría el Paraíso (algunos estudios recientes dicen que este paisaje podría corresponder a la zona norte del lago Como, en Italia). Además, con respecto a Judas Iscariote, se comenta que el modelo que Leonardo utilizó fue un verdadero criminal, pues da Vinci habría visitado distintas cárceles de Milán para tales efectos. Algunos también han postulado que el propio Leonardo Da Vinci se pintó a sí mismo en el rol del apóstol Judas Tadeo (un gran predicador que evangelizó a muchos pueblos y que fue el portador de la Sábana Santa después de la muerte de Cristo), aunque hay que consignar que la pintura data de 1495-1497, y en ese tiempo Leonardo tenía 45 años, mientras que el aspecto del apóstol, la penúltima figura de izquierda a derecha, es de mucha más edad.
 
La figura de Judas Tadeo, que en el extremo derecho del cuadro aparece conversando con el mismo Simón el Zelote, estaría basada por su parte en el filósofo Platón, un sabio que debido a sus planteamientos con respecto a la divinidad no era muy querido por la iglesia. Judas Tadeo y Simón el Zelote – o Da Vinci y Platón para algunos- a primera vista aparecen en “La última cena” manteniendo un tranquilo diálogo, ajenos a lo que sucede en la mesa, al revuelo creado, como si ellos estuvieran hablando de cosas más trascendentales e importantes.
         |
|
|
 Primer Primer
 Anterior
176 a 190 de 190
Siguiente Anterior
176 a 190 de 190
Siguiente
 Último
Último

|

