|
|
http://lucesquenobrillan.blogspot.com.ar/2014/01/la-probable-pronunciacion-del-nombre.html
La probable pronunciación del nombre que representa el tetragrámaton griego YHWH
Hoy día se conocen dos pronunciaciones del tetragrámaton o cuatro letras del hipotético nombre de Dios que en griego se escribe con las vocales YHWH (Ipsilon, Eta, Omega, Eta, son vocales, no consonantes), que en el alfabeto griego se pronuncian IEUE, respectivamente, o también IEOE, ya que la letra W (Omega, no uve doble) admite las dos pronunciaciones (U y O). Por lo general en las biblias de las iglesias protestantes el tetragramaton se transcribe como Jehovah. En las católicas, como Yahweh, forma ésta que, según los eruditos en la materia, sería la pronunciación más correcta del tetragramaton con que se representa el nombre divino. Otros eruditos defienden la forma Yahwah.
La pronunciación Jehovah se origina al haber intercalado la Iglesia Católica al tetragrámaton las vocales de la palabra Adonaí (Señor), supliendo la primera A por una E. Indistintamente se pronunciaba el nombre divino como Jehovah o Jehovih. La escritura y pronunciación Jehovah fue la más usada en las biblias católicas. Cuando los protestantes se separaron, adoptaron la forma Jehovah que aparece en sus biblias hasta este día. Posteriormente la Iglesia Católica, para diferenciar la pronunciación, adoptó la forma Yaweh que algunos estudiosos entendían como más correcta, pero que a día de hoy no se sabe si realmente lo es, y lo más probable es que no lo sea.
El historiador Diodoro de Sicilia, del siglo I antes de nuestra era, escribe que la pronunciación del tetragrámaton era IAO. La transcripción YHWH en griego habría conservado la pronunciación original hebrea. Según ello, una de dos, o las letras H no tendrían otra función que la de alargar el sonido vocal de las caracteres precedentes, a saber, Y, que se pronunciaría IAA, y W, con pronunciación de O alargada. La pronunciación sonaría, pues, como IAAOO; o bien ambas H eran mudas y el nombre sonaría como IAO ó YAHOH. No ha de olvidarse que el nombre divino abreviado aparece en la Biblia como YAH ó JAH.
Cada vez más eruditos están convencidos de que IAO ó YAHOH era la pronunciación correcta del tetragrámaton escrito YHWH en griego. Siglos atrás así lo habían creído estudiosos como Orígenes, Ireneo y Clemente de Alejandría, aunque este último defendía la expresión IAOU, dándole el sonido OU a la W. Tal pronunciación del hipotético nombre de Dios que esconde el tetragrámaton YHWH estaría de acuerdo con los arcaicos símbolos o caracteres representados como IO, donde la I se pronunciaba IA.
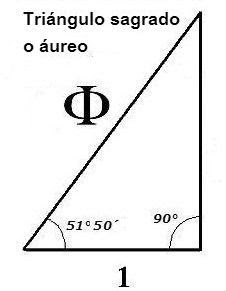
El símbolo I representaba en la antigüedad el concepto masculino, en tanto que O aludía al femenino. Ambos juntos forman IO, significando que la persona a quien se atribuyen los dos símbolos reúne en sí mismo los principios masculino y femenino, siendo el creador de cuanto existe, material o energéticamente. En griego los símbolos IO se funden en una sola letra, la que se denomina PHI, pronunciada F, que encaja el distintivo I en O. PHI es asimismo la designación del número áureo, de valor 1,618, empleado sobre todo en el arte arquitectónico maestro, algo que no está al alcance de todos los arquitectos. Por tanto PHI designa sapiencia profunda. No habría, pues, otra denominación más acorde para la sapiencia del Ser Creador que la representación IO, los principios masculino y femenino, ocultos en el tetragrámaton YHWH y pronunciado YAHOH ó IAO.
|
|
|
|
|
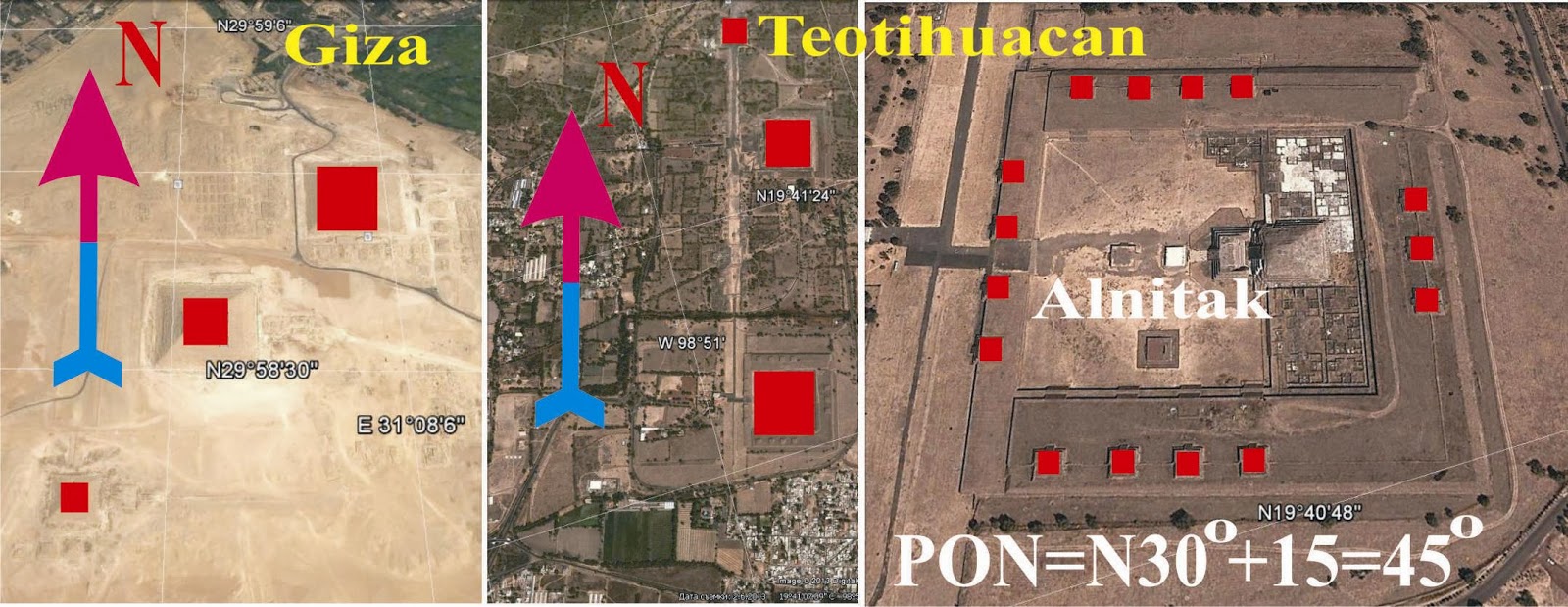
TEOTIHUACAN-GIZE-NUMERO DE ORO PHI=1.618-RELACION CON LA INDEPENDENCIA DEL ESTADO DE ISRAEL
ISRAEL
ISIS
RA
ELOHIM
330 AÑOS EXACTOS MAS 1618=1948 (INDEPENDENCIA DE ISRAEL)




¿Qué es phi?
Phi y la serie de Fibonacci
Funciones trigonométricas
Razones matemáticas
Pentágono
Espirales Áureas
Inicio :: Ver temas relacionados: Decalogo Geometria Sagrada :: Número de Oro :: Merkaba
¿Qué es phi?
Phi (1.618033988749895... ), pronunciado como fi, es un numero irracional como Pi ( 3.14159265358979... ), pero con muchas características matemáticas inusuales. Phi es la base de la Proporción Dorada. La razón o proporción determinada por Phi (1.618...) era conocida por los Griegos como la “Sección Dorada” y por los artistas del renacimiento como la “Proporción Divina”. También se le conoce como la razón Dorada o la Proporción Áurea.
Phi, como Pi, es una razón definida por una construcción geométrica.
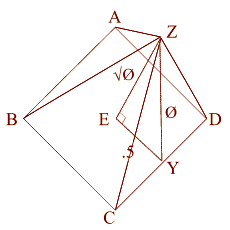
Pi es la relación de la circunferencia de un círculo respecto a su diámetro. Phi es la proporción de los segmentos de una línea que resultan cuando una línea es dividida de una forma única y especial.
La línea es dividida para que la proporción de la longitud de la línea entera (A) respecto a la longitud del segmento de la línea mayor (B) sea igual que la proporción de la longitud del segmento de la línea mayor (B) a la longitud del segmento de la línea menor (C)

Esto es que A es 1.618... veces B, y B es 1.618… veces C. Recíprocamente, C es 0.618... de B y B es 0.618... de A. Phi con mayúscula "Phi" es 1.6180339887..., mientras que phi con minúscula es 0.6180339887, el reciproco de Phi o Phi menos 1.
Lo que hace a phi incluso mas inusual es que puede derivarse de muchas formas y ser encontrado en proporcionalmente en el universo. Phi F puede ser derivado por: la serie numérica descubierta por Leonardo Fibonacci, matemáticas y geometría.
Phi y la serie de Fibonacci
Leonardo Fibonacci, por herencia del mundo árabe, descubrió la serie que nos lleva a phi. En el siglo XII, Leonardo Fibonacci descubrió una serie numérica simple que es la base de la increíble relación que encontramos detrás de phi. Empezando con 0 y 1, cada número de la serie es simplemente la suma de los dos anteriores. Así: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .
La razón (proporción) de cada par sucesivo de números en la serie se aproxima a phi (1.618. . .). Así si dividimos 5 entre 3 es 1.666..., y 8 entre 5 es 1.60. En la medida en la que vamos mas lejos del 0 (punto de inicio de la secuencia) nos acercamos al valor de phi.
La tabla de abajo nos muestra como las proporciones de números sucesivos en la serie Fibonacci se aproxima a Phi.
Puedes computar cualquier número de la serie Fibonacci fácilmente. Usa phi para saber cualquier numero (n) de la serie Fibonacci (f)
fn = Fn / 5½
Phi puede derivarse matemáticamente resolviendo la ecuación:
n2 - n1 - n0 = 0 que es lo mismo que n2 - n - 1 = 0
Esta ecuación la rescribimos y nos queda así:
n2 = n + 1 y 1 / n = n - 1
La solución a la ecuación es la raíz cuadrada de 5 más 1 dividido entre 2
( 5½ + 1 ) / 2 = 1.6180339... = F
Esto resulta en dos propiedades únicas de phi:
Si elevas al cuadrado a phi, obtienes un numero exactamente 1 mayor que phi: 2.6180...
F2 = F + 1
Si divides a phi entre 1, obtienes un numero exactamente a 1 menos phi: 0.6180...:
1 / F = F - 1
Phi, curiosamente, puede ser expresado en cinco: 5 ^ .5 * .5 + .5 = F
Puedes usar phi para computar un número n en la serie Fibonacci (fn): fn = Fn / 5½
Como por ejemplo, el número 40 de la serie Fibonacci es 102, 334, 155, que puede expresarse
f40 = F40 / 5½ = 102,334,155
Este método en realidad nos provee un estimado que siempre esta cerca del numero correcto Fibonacci.
http://www.iuca.net/gs/que%20es%20phi.htm









¿Qué es phi?
Phi y la serie de Fibonacci
Funciones trigonométricas
Razones matemáticas
Pentágono
Espirales Áureas
Inicio :: Ver temas relacionados: Decalogo Geometria Sagrada :: Número de Oro :: Merkaba
¿Qué es phi?
Phi (1.618033988749895... ), pronunciado como fi, es un numero irracional como Pi ( 3.14159265358979... ), pero con muchas características matemáticas inusuales. Phi es la base de la Proporción Dorada. La razón o proporción determinada por Phi (1.618...) era conocida por los Griegos como la “Sección Dorada” y por los artistas del renacimiento como la “Proporción Divina”. También se le conoce como la razón Dorada o la Proporción Áurea.
Phi, como Pi, es una razón definida por una construcción geométrica.
Pi es la relación de la circunferencia de un círculo respecto a su diámetro. Phi es la proporción de los segmentos de una línea que resultan cuando una línea es dividida de una forma única y especial.
La línea es dividida para que la proporción de la longitud de la línea entera (A) respecto a la longitud del segmento de la línea mayor (B) sea igual que la proporción de la longitud del segmento de la línea mayor (B) a la longitud del segmento de la línea menor (C)

Esto es que A es 1.618... veces B, y B es 1.618… veces C. Recíprocamente, C es 0.618... de B y B es 0.618... de A. Phi con mayúscula "Phi" es 1.6180339887..., mientras que phi con minúscula es 0.6180339887, el reciproco de Phi o Phi menos 1.
Lo que hace a phi incluso mas inusual es que puede derivarse de muchas formas y ser encontrado en proporcionalmente en el universo. Phi F puede ser derivado por: la serie numérica descubierta por Leonardo Fibonacci, matemáticas y geometría.
Phi y la serie de Fibonacci
Leonardo Fibonacci, por herencia del mundo árabe, descubrió la serie que nos lleva a phi. En el siglo XII, Leonardo Fibonacci descubrió una serie numérica simple que es la base de la increíble relación que encontramos detrás de phi. Empezando con 0 y 1, cada número de la serie es simplemente la suma de los dos anteriores. Así: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .
La razón (proporción) de cada par sucesivo de números en la serie se aproxima a phi (1.618. . .). Así si dividimos 5 entre 3 es 1.666..., y 8 entre 5 es 1.60. En la medida en la que vamos mas lejos del 0 (punto de inicio de la secuencia) nos acercamos al valor de phi.
La tabla de abajo nos muestra como las proporciones de números sucesivos en la serie Fibonacci se aproxima a Phi.
Puedes computar cualquier número de la serie Fibonacci fácilmente. Usa phi para saber cualquier numero (n) de la serie Fibonacci (f)
fn = Fn / 5½
Phi puede derivarse matemáticamente resolviendo la ecuación:
n2 - n1 - n0 = 0 que es lo mismo que n2 - n - 1 = 0
Esta ecuación la rescribimos y nos queda así:
n2 = n + 1 y 1 / n = n - 1
La solución a la ecuación es la raíz cuadrada de 5 más 1 dividido entre 2
( 5½ + 1 ) / 2 = 1.6180339... = F
Esto resulta en dos propiedades únicas de phi:
Si elevas al cuadrado a phi, obtienes un numero exactamente 1 mayor que phi: 2.6180...
F2 = F + 1
Si divides a phi entre 1, obtienes un numero exactamente a 1 menos phi: 0.6180...:
1 / F = F - 1
Phi, curiosamente, puede ser expresado en cinco: 5 ^ .5 * .5 + .5 = F
Puedes usar phi para computar un número n en la serie Fibonacci (fn): fn = Fn / 5½
Como por ejemplo, el número 40 de la serie Fibonacci es 102, 334, 155, que puede expresarse
f40 = F40 / 5½ = 102,334,155
Este método en realidad nos provee un estimado que siempre esta cerca del numero correcto Fibonacci.
http://www.iuca.net/gs/que%20es%20phi.htm





|
|
|
 Primer
Primer
 Anterior
2 a 4 de 34
Siguiente
Anterior
2 a 4 de 34
Siguiente Último
Último
|

