|
|
VERSICULO BIBLICO QUE "ANTICIPO" INFERNO, ESCRITO POR DAN BROWN
DAN BROWN= SERPIENTE= "AGUJERO DE GUSANO"
NOTEN EL NEXO DE DAN, CON LA SERPIENTE (VENECIA) Y EL CABALLO (PLAZA SAN MARCOS)
7. Génesis 49:17 Será Dan SERPIENTE junto al camino, Víbora junto a la senda, Que muerde los talones del caballo, Y hace caer hacia atrás al jinete.
|
|
7. Mateo 23:33 ¡Serpientes, generación de víboras! ¿Cómo escaparéis de la condenación del INFIERNO?
MONTE HERMON (TRIBU DE DAN)
DAN-IEL / PARALELO 33
MON / MOON / LUNA / TRANSFIGURACION
LINAJE DE A-DAN
|
|
|
| Reply |
Message 7 of 8 on the subject |
|
|
|
|
| Reply |
Message 8 of 8 on the subject |
|
| Reply |
Message 146 of 146 on the subject |
|
|
|
|
|
 First First  Previous 2 to 2 of 2 Next Previous 2 to 2 of 2 Next  Last Last  |
| Reply |
Message 2 of 2 on the subject |
|
68. Juan 4:10 Respondió Jesús y le dijo: Si conocieras el don de Dios, y quién es el que te dice: Dame de beber; tú le pedirías, y él te daría agua VIVA.
69. Juan 4:11 La mujer le dijo: Señor, no tienes con qué sacarla, y el pozo es hondo. ¿De dónde, pues, tienes el agua VIVA?
70. Juan 7:38 El que cree en mí, como dice la Escritura, de su interior correrán ríos de agua VIVA.
|
|
|
|
|
|
|
ISLA SAN GIORGIO (VENECIA)=GEORGE LEMAITRE
|
|
|
|
|

Jordan River (Utah)
From Wikipedia, the free encyclopedia
The Jordan River, in the state of Utah, United States, is a river about 51 miles (82 km) long. Regulated by pumps at its headwaters at Utah Lake, it flows northward through the Salt Lake Valley and empties into the Great Salt Lake. Four of Utah's six largest cities border the river: Salt Lake City, West Valley City, West Jordan, and Sandy. More than a million people live in the Jordan Subbasin, part of the Jordan River watershed that lies within Salt Lake and Utah counties. During the Pleistocene, the area was part of Lake Bonneville.
Members of the Desert Archaic Culture were the earliest known inhabitants of the region; an archaeological site found along the river dates back 3,000 years. Mormon pioneers led by Brigham Young were the first European American settlers, arriving in July 1847 and establishing farms and settlements along the river and its tributaries. The growing population, needing water for drinking, irrigation, and industrial use in an arid climate, dug ditches and canals, built dams, and installed pumps to create a highly regulated river.
Although the Jordan was originally a cold-water fishery with 13 native species, including Bonneville cutthroat trout, it has become a warm-water fishery where the common carp is most abundant. It was heavily polluted for many years by raw sewage, agricultural runoff, and mining wastes. In the 1960s, sewage treatment removed many pollutants. In the 21st century, pollution is further limited by the Clean Water Act, and, in some cases, the Superfund program. Once the home of bighorn sheep and beaver, the contemporary river is frequented by raccoons, red foxes, and domestic pets. It is an important avian resource, as are the Great Salt Lake and Utah Lake, visited by more than 200 bird species.
Big Cottonwood, Little Cottonwood, Red Butte, Mill, Parley's, and City creeks, as well as smaller streams like Willow Creek at Draper, Utah, flow through the sub-basin. The Jordan River Parkway along the river includes natural areas, botanical gardens, golf courses, and a 40-mile (64 km) bicycle and pedestrian trail, completed in 2017.[6]
The Jordan River is Utah Lake's only outflow. It originates at the northern end of the lake between the cities of Lehi and Saratoga Springs. It then meanders north through the north end of Utah Valley for approximately 8 miles (13 km) until it passes through a gorge in the Traverse Mountains, known as the Jordan Narrows. The Utah National Guard base at Camp Williams lies on the western side of the river through much of the Jordan Narrows.[7][8] The Turner Dam, located 41.8 miles (67.3 km) from the river's mouth (or at river mile 41.8) and within the boundaries of the Jordan Narrows, is the first of two dams of the Jordan River. Turner Dam diverts the water to the right or easterly into the East Jordan Canal and to the left or westerly toward the Utah and Salt Lake Canal. Two pumping stations situated next to Turner Dam divert water to the west into the Provo Reservoir Canal, Utah Lake Distribution Canal, and Jacob-Welby Canal. The Provo Reservoir Canal runs north through Salt Lake County, Jacob-Welby runs south through Utah County. The Utah Lake Distribution Canal runs both north and south, eventually leading back into Utah Lake.[9] Outside the narrows, the river reaches the second dam, known as Joint Dam, which is 39.9 miles (64.2 km) from the river's mouth. Joint Dam diverts water to the east for the Jordan and Salt Lake City Canal and to the west for the South Jordan Canal.[10][11][12]
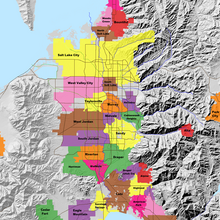
Map of the Salt Lake Valley
The river then flows through the middle of the Salt Lake Valley, initially moving through the city of Bluffdale and then forming the border between the cities of Riverton and Draper.[7] The river then enters the city of South Jordan where it merges with Midas Creek from the west. Upon leaving South Jordan, the river forms the border between the cities of West Jordan on the west and Sandy and Midvale on the east. From the west, Bingham Creek enters West Jordan. Dry Creek, an eastern tributary, combines with the main river in Sandy. The river then forms the border between the cities of Taylorsville and West Valley City on the west and Murray and South Salt Lake on the east. The river flows underneath Interstate 215 in Murray. Little and Big Cottonwood Creeks enter from the east in Murray, 21.7 miles (34.9 km) and 20.6 miles (33.2 km) from the mouth respectively. Mill Creek enters on the east in South Salt Lake, 17.3 miles (27.8 km) from the mouth. The river runs through the middle of Salt Lake City, where the river travels underneath Interstate 80 a mile west of downtown Salt Lake City and again underneath Interstate 215 in the northern portion of Salt Lake City. Interstate 15 parallels the river's eastern flank throughout Salt Lake County. At 16 miles (26 km) from the mouth, the river enters the Surplus Canal channel. The Jordan River physically diverts from the Surplus Canal through four gates and heads north with the Surplus Canal heading northwest. Parley's, Emigration, and Red Butte Creeks converge from the east through an underground pipe, 14.2 miles (22.9 km) from the mouth.[7] City Creek also enters via an underground pipe, 11.5 miles (18.5 km) from the river's mouth. The length of the river and the elevation of its mouth varies year to year depending on the fluctuations of the Great Salt Lake caused by weather conditions. The lake has an average elevation of 4,200 feet (1,300 m) which can deviate by 10 feet (3.0 m).[3] The Jordan River then continues for 9 to 12 miles (14 to 19 km) with Salt Lake County on the west and North Salt Lake and Davis County on the east until it empties into the Great Salt Lake.[7][8][11]
Discharge[edit]
The United States Geological Survey maintains a stream gauge in Salt Lake City that shows annual runoff from the period 1980–2003 is just over 150,000 acre-feet (190,000,000 m3) per year or 100 percent of the total 800,000 acre-feet (990,000,000 m3) of water entering the Jordan River from all sources. The Surplus Canal carries almost 60 percent of the water into the Great Salt Lake, with various irrigation canals responsible for the rest. The amount of water entering the Jordan River from Utah Lake is just over 400,000 acre-feet (490,000,000 m3) per year. Inflow from the 11 largest streams feeding the Jordan River, sewage treatment plants, and groundwater each account for approximately 15 percent of water entering the river.[13]
Watershed[edit]
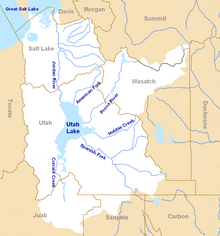
Map of the entire Jordan River Basin
|
|
|
|
|

The letter S is the 19th letter of the Latin alphabet and the English alphabet. It is also used in other Western European languages and other Latin alphabets.
   
POPE NUMBER 266
9 LUNAR MONTHS=266 DAYS
FR-ANC-ISCO / J-ANUK-A
1/1-23/9 GREGORIAN CALENDAR=266 DAYS
266 DAYS=19*2*7 DAYS (SATURDAY)=WOMAN IN PREGNANT=LUNAR PHASE (36=4*9) (1+2+3+4+...36=666)
10/3-30/11 (JANUKAH=JOHN 10 22=24/9-KISLEV HAGGAI 2 10 )=266 DAYS
10 On the twenty-fourth day of the ninth month, in the second year of Darius, the word of the Lord came by Haggai the prophet, 11 “Thus says the Lord of hosts: Ask the priests about the law: 12 ‘If someone carries holy meat in the fold of his garment and touches with his fold bread or stew or wine or oil or any kind of food, does it become holy?’” The priests answered and said, “No.” 13 Then Haggai said, “If someone who is unclean by contact with a dead body touches any of these, does it become unclean?” The priests answered and said, “It does become unclean.” 14 Then Haggai answered and said, “So is it with this people, and with this nation before me, declares the Lord, and so with every work of their hands. And what they offer there is unclean. 15 Now then, consider from this day onward. Before stone was placed upon stone in the temple of the Lord, 16 how did you fare? When one came to a heap of twenty measures, there were but ten. When one came to the wine vat to draw fifty measures, there were but twenty. 17 I struck you and all the products of your toil with blight and with mildew and with hail, yet you did not turn to me, declares the Lord. 18 Consider from this day onward, from the twenty-fourth day of the ninth month. Since the day that the foundation of the Lord's temple was laid, consider: 19 Is the seed yet in the barn? Indeed, the vine, the fig tree, the pomegranate, and the olive tree have yielded nothing. But from this day on I will bless you.”


|
|
|
 Primer Primer
 Anterior
65 a 79 de 79
Següent Anterior
65 a 79 de 79
Següent
 Darrer
Darrer

|

