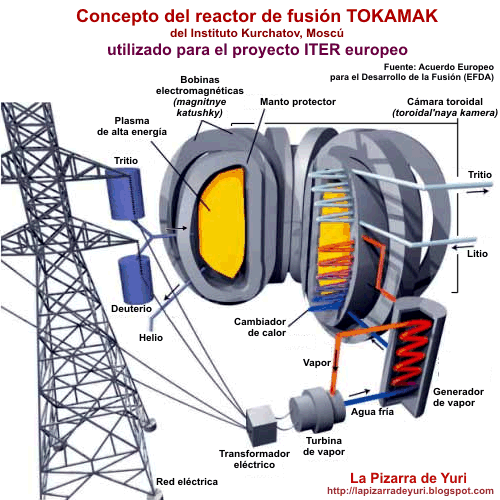
The Louvre is the Moon Pyramid. It encodes canonical distances that relate to the moon. This famous museum in Paris reveals esoteric wisdom but only for those with the eyes to see.
The surface of the Louvre is covered in glass panes. If we examine the angular measures of each glass polygon and sum them up we get the canonical distance between Earth and Moon, in miles. The Moon doesn’t revolve around Earth in a perfect circle, it’s more of an ellipse. When it is closer to Earth it is called perigee (close to Moon). When the moon is farthest from Earth it is called apogee (apart from Moon). These distances are 225,622 miles and 252,088 miles respectively.
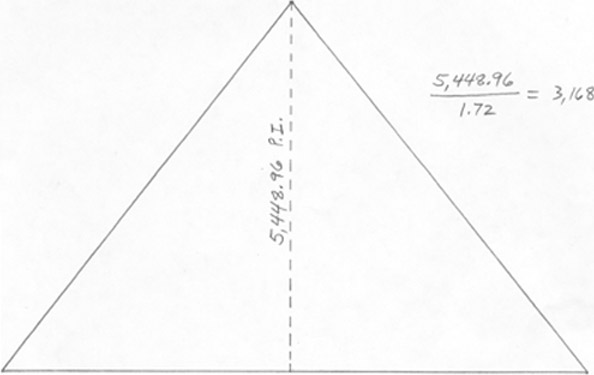
On each of the four sides there are 153 rhombi and 18 triangles at the bottom.
Rhombi have 360° in their angles, and triangles contain 180°.
153 x 360° = 55,080°
18 x 180° = 3240°
55,080 + 3240 = 58,320°
58,320 x 4 = 233,280° degrees on the outer surface of the Louvre Pyramid.
This is a great estimation for the distance the Moon is from Earth, in miles. This would seem to be an obvious flaw in reasoning since we are mixing units. What do degrees have anything to do with miles?
The origin of the mile, and most other metrics, are based on the actual dimensions of Earth. For instance a meter is one 40 millionth of the polar circumference of Earth. The distances of the planets in the solar system and the sun are proportioned to a canon of number reflected in our units of measure, such as feet, miles, and furlongs.
You’ll notice they always reduce to nine, kabbalistically. i.e. 2160, the diameter of the Moon in miles(99.99%), equals 9 because 2+1+6+0= 9.
Or the diameter of the moon, in furlongs, is 17,280 (1+7+2+8+0=9)
This technique of reducing numbers down to one digit is called many names. In Vortex Based Mathematics they call the result the ‘digital root’. The digital root of 55 is 1, because 5+5=10. And 1+0=1.
The digital root of 432 is 9
The digital root of 108, another highly revered number in theosophy, is also 9.
You’ll notice that many of the numbers we commonly use today to measure time, distance, volume, area, angle, etc, all reduce to 9.
According to NASA there is a point in time, between perigee and apogee, when the Moon is exactly 233,280 miles from Earth. Another way you can think of this is, at this point, the Moon is 108 Moon diameters(2160 miles) away from Earth. It’s interesting to note that the Sun is about 108 ‘sun diameters’ away from Earth and about 108 Earths fit across the diameter of the Sun. 108 is a sacred number in almost every religion. Say a prayer and then count the number beads on your mala.
The Louvre Pyramid not only echoes the canonical distance between Earth and Moon(2160×108), but it also encodes the number of full moons in a year. √153 = 12.369. There are 12.369 full moons every year (99.99%). Each side of the Louvre Pyramid is composed of 153 rhombi. 153, as it turns out is also a sacred number.
Jesus said to them, “Bring some of the fish you have just caught.” So Simon Peter climbed back into the boat and dragged the net ashore. It was full of large fish, 153, but even with so many the net was not torn.
John, 21:11
Why 153? Why not any other number? Is this really arbitrary or are they trying to tell us something? (153 also digitally reduces to 9, as 1+5+3=9.
Astrologically, we are in the age of Pisces, or the age of the Fish. 153 is derived from the vesica pisces and the square root of three.(1.732..) The ratio 265:153 is a great approximation of √3. 265:153 is essentially the same as √3:1 or 1.732:1

We can see why the bible relates 153 to fish, as the vesica pisces literally translates to ‘bladder of the fish’ in Latin, and the number 153 is encoded into the sacred geometry of the vesica pisces, which represents duality. As unity (the circle) decides to double itself into duality, it creates this almond shaped geometry that is mentioned in the bible, and temporally apparent in our solar system. The Jesus-Fish bumper sticker probably makes a lot more sense now.
Coincidentally, or not, turbot and brill fish (Scophthalmus rhombus), also exhibit this rhombic geometry.
A factorial is simply all the numbers below it multiplied together.
3! = 1 x 2 x 3
So, factorial three equals six
153 is coincidentally (or not) the sum of the first 5 factorials
1! + 2! + 3! + 4! + 5! = 153
153 is the 17th triangular number(see below)
153 is also a narcissistic number, in that, 1 cubed + 5 cubed + 3 cubed = 153

153: a very auspicious number (img courtesy of Infinity-Codes)
The diameter of the Moon can also be approximated using factorials, as 2160 miles = (1x2x3x4x5x6) x 3. The same could be said for Earth’s diameter of 7920 miles (99.97%). 7920 = 11!/7! ,or more simply: 8x9x10x11 miles The Moon’s radius, 1080 miles, plus Earth’s radius(3960 miles), equals 5040.
5040 = 1x2x3x4x5x6x7
5040 = 7!
5040 = 7x8x9x10
5040 = 10!/6!
7 divides the ‘decad’, or the 10 numbers in our decimal system, in half. This is why Pythagoras considered 7 to be the middle ground among the ten numbers, and not 5 like you would think. If we add these two factorial sums together we get the number of minutes in a week, 10,080 (5040 x 2). And of course, there are 7 days in a week.
As you can see, talking about one number alone is next to impossible, as it draws you into another numeric connection. 153, 5040, 108, 432, the list of sacred numbers goes on and on… It is the quality of the number that is important, not just the mere quantity.
“Numbers are Real and Alive not merely symbols for other things. You will discover that the relationships between numbers are not random or man-made but that numbers are actually elementary particles of which everything is composed. This lost knowledge was well known to our ancients and is now being uncovered for us today” -Rhuben Neal (Barbitone)
“Pythagoras was one of the first teachers to establish a community wherein all the members were of mutual assistance to one another in the common attainment of the higher sciences. He also introduced the discipline of retrospection as essential to the development of the spiritual mind. Pythagoreanism may be summarized as a system of metaphysical speculation concerning the relationships between numbers and the causal agencies of existence.” -Manly P. Hall