|
Réponse |
Message 1 de 91 de ce thème |
|
ISRAEL=ISIS-RA-ELOHIM / RA/ RELOJ/ RESURRECCION / LETRA R/ RAHABIT / RAQUEL (MADRE DE BENJAMIN (LOBO/ PERRO)
|
|
EL CONEJO ES SIMBOLO DE FERTILIDAD Y SE REPRODUCE CON EL NUMERO DE ORO
LA LEY DE LA RELATIVIDAD DE EINSTEIN TIENE QUE VER CON LA RELATIVIDAD DEL TIEMPO EN FUNCION A LA MASA Y LA VELOCIDAD DE LA LUZ
| Reply |
Message 52 of 52 on the subject |
|
|
|
|
|
MON-KEY/MON-DAY/MON-EY-E/LLAVE DEL MONO/MOON /LUNA/ RAQUEL (GENESIS 37)
|
|
|
|
Réponse |
Message 62 de 91 de ce thème |
|
Fibonacci 24 Repeating Pattern
May 15, 2012 by Gary Meisner
The Fibonacci sequence has a pattern that repeats every 24 numbers.
Numeric reduction is a technique used in analysis of numbers in which all the digits of a number are added together until only one digit remains. As an example, the numeric reduction of 256 is 4 because 2+5+6=13 and 1+3=4.
Applying numeric reduction to the Fibonacci series produces an infinite series of 24 repeating digits:
1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9
If you take the first 12 digits and add them to the second twelve digits and apply numeric reduction to the result, you find that they all have a value of 9.
| 1st 12 numbers |
1 |
1 |
2 |
3 |
5 |
8 |
4 |
3 |
7 |
1 |
8 |
9 |
| 2nd 12 numbers |
8 |
8 |
7 |
6 |
4 |
1 |
5 |
6 |
2 |
8 |
1 |
9 |
| Numeric reduction – Add rows 1 and 2 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
18 |
| Final numeric reduction – Add digits of result |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
This pattern was contributed both by Joseph Turbeville and then again by a mathematician by the name of Jain.
We would expect a pattern to exist in the Fibonacci series since each number in the series encodes the sum of the previous two. What’s not quite so obvious is why this pattern should repeat every 24 numbers or why the first and last half of the series should all add to 9.
For those of you from the “Show Me” state, this pattern of 24 digits is demonstrated in the numeric reduction of the first 73 numbers of the Fibonacci series, as shown below:
|
Fibonacci Number
|
Numeric reduction by adding digits |
| 1st Level |
2nd Level |
Final Level |
| Example: 2,584 |
2+5+8+4=19 |
1+9=10 |
1+0=1 |
| 0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
| 2 |
2 |
2 |
2 |
| 3 |
3 |
3 |
3 |
| 5 |
5 |
5 |
5 |
| 8 |
8 |
8 |
8 |
| 13 |
4 |
4 |
4 |
| 21 |
3 |
3 |
3 |
| 34 |
7 |
7 |
7 |
| 55 |
10 |
1 |
1 |
| 89 |
17 |
8 |
8 |
| 144 |
9 |
9 |
9 |
| 233 |
8 |
8 |
8 |
| 377 |
17 |
8 |
8 |
| 610 |
7 |
7 |
7 |
| 987 |
24 |
6 |
6 |
| 1,597 |
22 |
4 |
4 |
| 2,584 |
19 |
10 |
1 |
| 4,181 |
14 |
5 |
5 |
| 6,765 |
24 |
6 |
6 |
| 10,946 |
20 |
2 |
2 |
| 17,711 |
17 |
8 |
8 |
| 28,657 |
28 |
10 |
1 |
| 46,368 |
27 |
9 |
9 |
| 75,025 |
19 |
10 |
1 |
| 121,393 |
19 |
10 |
1 |
| 196,418 |
29 |
11 |
2 |
| 317,811 |
21 |
3 |
3 |
| 514,229 |
23 |
5 |
5 |
| 832,040 |
17 |
8 |
8 |
| 1,346,269 |
31 |
4 |
4 |
| 2,178,309 |
30 |
3 |
3 |
| 3,524,578 |
34 |
7 |
7 |
| 5,702,887 |
37 |
10 |
1 |
| 9,227,465 |
35 |
8 |
8 |
| 14,930,352 |
27 |
9 |
9 |
| 24,157,817 |
35 |
8 |
8 |
| 39,088,169 |
44 |
8 |
8 |
| 63,245,986 |
43 |
7 |
7 |
| 102,334,155 |
24 |
6 |
6 |
| 165,580,141 |
31 |
4 |
4 |
| 267,914,296 |
46 |
10 |
1 |
| 433,494,437 |
41 |
5 |
5 |
| 701,408,733 |
33 |
6 |
6 |
| 1,134,903,170 |
29 |
11 |
2 |
| 1,836,311,903 |
35 |
8 |
8 |
| 2,971,215,073 |
37 |
10 |
1 |
| 4,807,526,976 |
54 |
9 |
9 |
| 7,778,742,049 |
55 |
10 |
1 |
| 12,586,269,025 |
46 |
10 |
1 |
| 20,365,011,074 |
29 |
11 |
2 |
| 32,951,280,099 |
48 |
12 |
3 |
| 53,316,291,173 |
41 |
5 |
5 |
| 86,267,571,272 |
53 |
8 |
8 |
| 139,583,862,445 |
58 |
13 |
4 |
| 225,851,433,717 |
48 |
12 |
3 |
| 365,435,296,162 |
52 |
7 |
7 |
| 591,286,729,879 |
73 |
10 |
1 |
| 956,722,026,041 |
44 |
8 |
8 |
| 1,548,008,755,920 |
54 |
9 |
9 |
| 2,504,730,781,961 |
53 |
8 |
8 |
| 4,052,739,537,881 |
62 |
8 |
8 |
| 6,557,470,319,842 |
61 |
7 |
7 |
| 10,610,209,857,723 |
51 |
6 |
6 |
| 17,167,680,177,565 |
67 |
13 |
4 |
| 27,777,890,035,288 |
73 |
10 |
1 |
| 44,945,570,212,853 |
59 |
14 |
5 |
| 72,723,460,248,141 |
51 |
6 |
6 |
| 117,669,030,460,994 |
65 |
11 |
2 |
| 190,392,490,709,135 |
62 |
8 |
8 |
| 308,061,521,170,129 |
46 |
10 |
1 |
| 498,454,011,879,264 |
72 |
9 |
9 |
Thanks to Joseph Turbeville for sending “A Glimmer of Light from the Eye of a Giant” and to Helga Hertsig for bringing Jain’s discovery of this pattern to my attention.
Filed Under: Math
https://www.goldennumber.net/fibonacci-24-pattern/ |
|
|
|
Réponse |
Message 63 de 91 de ce thème |
|
Fibonacci 60 Repeating Pattern
October 30, 2016 by Gary Meisner
The last digit of the numbers in the Fibonacci Sequence form a pattern that repeats after every 60th number:
0, 1, 1, 2, 3, 5, 8, 3, 1, 4, 5, 9, 4, 3, 7, 0, 7, 7, 4, 1, 5, 6, 1, 7, 8, 5, 3, 8, 1, 9, 0, 9, 9, 8, 7, 5, 2, 7, 9, 6, 5, 1, 6, 7, 3, 0, 3, 3, 6, 9, 5, 4, 9, 3, 2, 5, 7, 2, 9, 1
This pattern can be seen in the following list of the first 72 Fibonacci numbers:
| 0 |
0 |
| 1 |
1 |
| 2 |
1 |
| 3 |
2 |
| 4 |
3 |
| 5 |
5 |
| 6 |
8 |
| 7 |
13 |
| 8 |
21 |
| 9 |
34 |
| 10 |
55 |
| 11 |
89 |
| 12 |
144 |
| 13 |
233 |
| 14 |
377 |
| 15 |
610 |
| 16 |
987 |
| 17 |
1,597 |
| 18 |
2,584 |
| 19 |
4,181 |
| 20 |
6,765 |
| 21 |
10,946 |
| 22 |
17,711 |
| 23 |
28,657 |
| 24 |
46,368 |
| 25 |
75,025 |
| 26 |
121,393 |
| 27 |
196,418 |
| 28 |
317,811 |
| 29 |
514,229 |
| 30 |
832,040 |
| 31 |
1,346,269 |
| 32 |
2,178,309 |
| 33 |
3,524,578 |
| 34 |
5,702,887 |
| 35 |
9,227,465 |
| 36 |
14,930,352 |
| 37 |
24,157,817 |
| 38 |
39,088,169 |
| 39 |
63,245,986 |
| 40 |
102,334,155 |
| 41 |
165,580,141 |
| 42 |
267,914,296 |
| 43 |
433,494,437 |
| 44 |
701,408,733 |
| 45 |
1,134,903,170 |
| 46 |
1,836,311,903 |
| 47 |
2,971,215,073 |
| 48 |
4,807,526,976 |
| 49 |
7,778,742,049 |
| 50 |
12,586,269,025 |
| 51 |
20,365,011,074 |
| 52 |
32,951,280,099 |
| 53 |
53,316,291,173 |
| 54 |
86,267,571,272 |
| 55 |
139,583,862,445 |
| 56 |
225,851,433,717 |
| 57 |
365,435,296,162 |
| 58 |
591,286,729,879 |
| 59 |
956,722,026,041 |
| 60 |
1,548,008,755,920 |
| 61 |
2,504,730,781,961 |
| 62 |
4,052,739,537,881 |
| 63 |
6,557,470,319,842 |
| 64 |
10,610,209,857,723 |
| 65 |
17,167,680,177,565 |
| 66 |
27,777,890,035,288 |
| 67 |
44,945,570,212,853 |
| 68 |
72,723,460,248,141 |
| 69 |
117,669,030,460,994 |
| 70 |
190,392,490,709,135 |
| 71 |
308,061,521,170,129 |
| 72 |
498,454,011,879,264 |
Lucien Khan arranged these 60 digits of the pattern in a circle, as shown in illustration below:
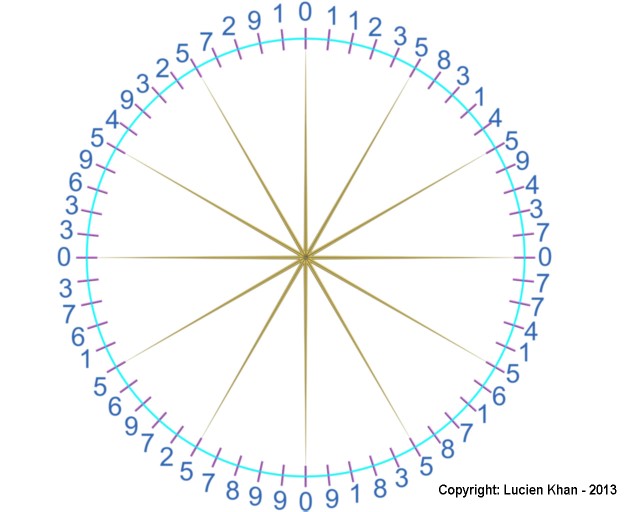
Here he found other interesting results:
- The zeros align with the 4 cardinal points on a compass.
- The fives align with the 8 other points of the 12 points on a clock.
- Except for the zeros, the number directly opposite each number adds to 10.
Lucien postulates that ancient knowledge of these relationships contributed to the development of our modern use of 60 minutes in an hour, and presentation of numbers on the face of the clock.
I found too that any group of four numbers that are 90 degrees from each other (15 away from each other in the circle) sum to 20, except again for the zeros. As an example, use 1, 7, 9 and 3, which appear one to the right of each of the compass points.
Additionally, every group of five numbers that define the points of the 12 pentagons on the circle also create a pattern. Four of the pentagons have even-numbered last digits of 0, 2, 4, 6, and 8. The remaining eight pentagons have odd-numbered last digits of 1, 3, 5, 7 and 9.
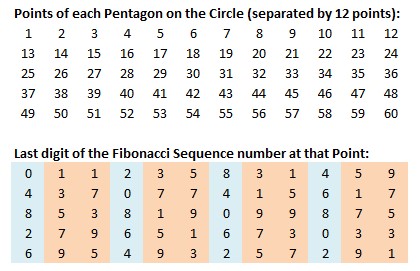
Another interesting pattern yet was observed by Lucien Khan: The 216th number is this sequence is 619220451666590135228675387863297874269396512. The sum of all the digits in that number add up to 216, as well. He notes that it is believed that the secret or hidden name of God contains 216 characters. There are many other fascinating relationships and sacred geometries, which are presented by Lucien Khan in more detail at the links below.
https://www.goldennumber.net/fibonacci-60-repeating-pattern/ |
|
|
|
Réponse |
Message 64 de 91 de ce thème |
|
|
|
|
Réponse |
Message 65 de 91 de ce thème |
|
|
|
|
Réponse |
Message 66 de 91 de ce thème |
|
|
|
|
Réponse |
Message 67 de 91 de ce thème |
|
|
|
|
Réponse |
Message 68 de 91 de ce thème |
|
21/6=MANO DE DIOS DE MARADONA
|
|
|
|
Réponse |
Message 69 de 91 de ce thème |
|
|
|
|
Réponse |
Message 70 de 91 de ce thème |
|
|
|
|
Réponse |
Message 71 de 91 de ce thème |
|
|
|
|
Réponse |
Message 72 de 91 de ce thème |
|
|
|
|
Réponse |
Message 73 de 91 de ce thème |
|
|
|
|
Réponse |
Message 74 de 91 de ce thème |
|
The amount of days in a solar year plus the proportions for the Equatorial circumference of the Earth and the proportions of the Great Pyramid of Giza according to Golden Pi = 4/√φ = 3.144605511029693144: The Great Pyramid of Giza is a geodetic model of Planet Earth. The measurements mentioned below are the ideal measurements. A meter is equal to 100 centimeters 1 Solon cubit = 40 times √φ = 50.88078598056276 centimeters. If 1 Solon cubit is divided into 20 equal units of measure then 20 inches can be derived because 1 Solon cubit is equal to 20 inches. 1 Saylen cubit = 50 times √φ = 63.60098247570345 centimeters. If 1 Saylen cubit is divided into 25 equal units of measure then 25 inches can be derived because 1 Saylen cubit is equal to 25 inches. 1 inch = 2 times √φ = 2.544039299028138 centimeters. 1 foot = 12 inches. 1 foot = 24 times √φ = 30.528471588337656 centimeters. If the shortest edge length of a Kepler right triangle is equal to 1 then the hypotenuse of the Kepelr right triangle is equal to The Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 according to the Pythagorean theorem. The Golden ratio in Trigonometry = (cosine (36 degrees) times 2) = 1.618033988749895. If the shortest edge length of a Kepler right triangle is equal to 1 then second longest edge length of the Kepelr right triangle is the square root of the Golden ratio = √φ = 1.272019649514069 according to the Pythagorean theorem. The width for the square base of the Great Pyramid of Giza is equal to 756 feet. • If the shortest edge length of a Kepler right triangle is equal to 1 foot and then the second edge length of the Kepler right triangle is multiplied 378 equal times the result will be the height of the Great Pyramid of Giza = 378 times √φ = 480.823427516318082 feet according to Golden Pi = 4/√φ = 3.144605511029693144. • If the shortest edge length of a Kepler right triangle is equal to 1 foot and then the hypotenuse of the Kepler right triangle is multiplied 378 equal times the result will be the slant height of the Great Pyramid of Giza = 378 times φ = 611.61684774746031 feet according to Golden Pi = 4/√φ = 3.144605511029693144. • If the shorter edge length of a Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 rectangle is equal to 1 foot and then the diagonal of the Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 rectangle is multiplied 378 equal times the result will be the edge height of the Great Pyramid of Giza = 378 times = Cosine (18) degrees times 2 = 1.902113032590307 = 718.998726319136046 feet according to Golden Pi = 4/√φ = 3.144605511029693144.Cosine (18) degrees times 2 = 1.902113032590307. Cosine (18) degrees times 2 = 1.902113032590307 squared = φ plus 2 = 3.618033988749895. • If the shortest edge length of a Kepler right triangle is equal to 1 foot = 24 times √φ = 30.528471588337656 centimeters then the second longest edge length of that Kepler right triangle is equal to 38.832815729997479 centimeters.24 times √φ = 30.528471588337656 centimeters times the square root of the Golden ratio = √φ = 1.272019649514069 = 38.832815729997479 centimeters. 1 foot = 24 times √φ = 30.528471588337656 centimeters times the square root of the Golden ratio = √φ = 1.272019649514069 = 38.832815729997479 centimeters times 378 = the height of the Great Pyramid of Giza of Giza = 14678.804345939047062 centimeters. The height of the Great Pyramid of Giza = 14678.804345939047062 centimeters divided by 24 times √φ = 30.528471588337656 centimeters = the height of the Great Pyramid of Giza = 480.823427516318088 feet. 378 times √φ = 1.272019649514069 = 480.823427516318088. • If the shortest edge length of a Kepler right triangle is equal to 1 foot = 24 times √φ = 30.528471588337656 centimeters then the hypotenuse of that Kepler right triangle is equal to 49.39610465451582 centimeters. 24 times √φ = 30.528471588337656 centimeters times the Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 = 49.39610465451582 centimeters. 1 foot = 24 times √φ = 30.528471588337656 centimeters times the Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 378 = 49.39610465451582 centimeters times 378 = slant the height of the Great Pyramid of Giza = 18671.727559406979971centimeters. The Slant height of the Great Pyramid = 18671.727559406979971 centimeters divided by 24 times √φ = 30.528471588337656 centimeters = the slant height of the Great Pyramid of Giza = 611.61684774746031 feet. 378 times √φ = 1.272019649514069 = 611.61684774746031. • If the shortest edge length of a Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 rectangle is equal to 1 foot = 24 times √φ = 30.528471588337656 centimeters then the length of the diagonal of that Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 rectangle is equal to 58.068603673239965 centimeters. 24 times √φ = 30.528471588337656 centimeters times Cosine (18) degrees times 2 = 1.902113032590307 = 58.068603673239965 centimeters. Cosine (18) degrees times 2 = 1.902113032590307 squared = φ plus 2 = 3.618033988749895. 1 foot = 24 times √φ = 30.528471588337656 centimeters times = Cosine (18) degrees times 2 = 1.902113032590307 = 58.068603673239965 centimeters times 378 = the edge height of the Great Pyramid of Giza of Giza = 21949.932188484706835 centimeters. The edge height of the Great Pyramid = 21949.932188484706835 centimeters divided by 24 times √φ = 30.528471588337656 centimeters = the edge height of the Great Pyramid of Giza = 718.998726319136046 feet. 378 times Cosine (18) degrees times 2 = 1.902113032590307 = 718.998726319136046. Cosine (18) degrees times 2 = 1.902113032590307. Cosine (18) degrees times 2 = 1.902113032590307 squared = φ plus 2 = 3.618033988749895. A Kepler right triangle can be created from the construction of a Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 rectangle by using Compass and straight edge and obviously a marker for the drawing surface. The amount of days in a Solar year = 4/√φ times 7920 times 5280/(10 ^ 3 times 360) = 365.277376161209156. The amount of days in a Solar year = 4/√φ = 3.144605511029693144 times 7920 times 5280/(10 ^ 3 times 360) = 365.277376161209156. The equatorial circumference of planet Earth = 10 ^ 3 times 360 times 365.277376161209156 = 131499855.41803529616 feet. The equatorial circumference of planet Earth = 4/√φ = 3.144605511029693144 times 7920 = 24905.275647355169727 statute miles. 131499855.41803529616 feet divided by 86400 = half the perimeter of the socle of the Great Pyramid of Giza = 1521.989067338371483 feet. Half the perimeter of the socle of the Great Pyramid of Giza times 86400 is also equal to the equatorial circumference of planet Earth = 131499855.41803529616 feet. 484 divided by √φ times 2 = the width of the socle of the Great Pyramid of Giza = 760.99453366918572 feet. Half the width of the socle of the Great Pyramid of Giza = 380.49726683459286 feet times √φ = 484 feet. 484/√φ times 2 times 2 times 86400 = 131499855.41803529616 feet. 131499855.41803529616 feet divided by 5280 = The perimeter of the socle of the Great Pyramid of Giza = 484/√φ times 8 = 3043.978134676742966 feet. 484 feet /√φ times 8 = 3043.978134676742966 feet times 12 = 24905.275647355169727 statute miles. 24905.275647355169727 statute miles divided by 7920 statute miles = Golden Pi = 4/√φ = 3.144605511029693144. There are 929.28 meters in the square perimeter of the socle of the Great Pyramid of Giza according to Golden Pi = 4/√φ = 3.144605511029693144. 484/√φ times 8 = 3043.978134676742966 times 12 = 36527.737616120915592 divided by 100 = the exact amount of days in a solar year = 365.277376161209156. The equatorial diameter of our planet Earth = 41817600 feet. 41817600 feet divided 86400 = the height of the Great Pyramid of Giza = 378 times √φ = 480.823427516318082 feet plus the height of the socle of the Great Pyramid of Giza = 3.176572483681918 feet. 10 ^ 3 times 360 times 484/(√φ) times 8 times 12/(100) = 131499855.41803529616 feet. The height of the Great Pyramid if Giza is 378 times √φ = 480.823427516318082 feet. The width of the square base of the Great Pyramid of Giza is 756 feet. The perimeter of the square base of the Great Pyramid of Giza = 3024 feet. 9 factorial = 362880. At 10 degrees latitude the length of a degree is 9 factorial =362880 feet. The amount of inches in the perimeter of the square of the Great Pyramid of Giza = 36288. 36288 times 10 = 362880. The width for the square base of the Great Pyramid of Giza = 756 feet. The perimeter of the square base of the Great Pyramid of Giza = 3024 feet. There are 36288 inches in the perimeter of the square base of the Great Pyramid of Giza. 3024 times 12 = 36288. 756 times 4 times 12 = 36288. (9!)/10 = 36288. The equatorial circumference of planet Earth: https://joedubs.com/four-earthly-elements/equatorial-circumference-of-earth/ Kepler right triangle diagram with squares upon the edges of the Kepler right triangle: https://drive.google.com/file/d/1iBtXYy06yv9UWtGP5mwMXyt80vaysFvR/view?usp=sharing Kepler right triangle construction method: https://drive.google.com/file/d/15DNXB_xNP2f2jCroC0FyNUyBYGhVAA2J/view?usp=sharing PYTHAGOREAN THEOREM: https://en.wikipedia.org/wiki/Pythagorean_theorem Golden ratio: https://en.wikipedia.org/wiki/Golden_ratio The history of the meter: The history of the meter: https://www.factinate.com/editorial/meter-history/ The meter: https://en.wikipedia.org/wiki/Metre The meter is based now on the speed of light: https://www.youtube.com/watch?v=vgqUyFaUDcI |
|
|
|
Réponse |
Message 75 de 91 de ce thème |
|
|
|
|
Réponse |
Message 76 de 91 de ce thème |
|
|
|
 Premier Premier
 Précédent
62 a 76 de 91
Suivant Précédent
62 a 76 de 91
Suivant Dernier
Dernier
|


.jpg)














