ANCIENT EGYPTIAN GEODESY - PART II
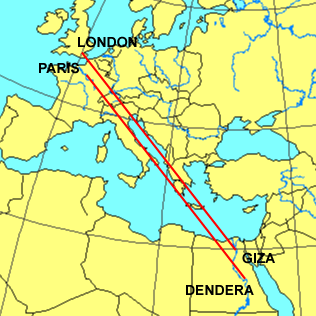
The great circle alignment from Giza to Alexandria has an azimuth of 51.85° north of due west from Giza (the same angle as the slope of the Great Pyramid). Extended beyond Alexandria, this great circle also crosses over Delphi, Rollright and Newgrange, as well as the city of London.

Map image © VectorGlobe
The azimuth of a great circle alignment from Dendera to Paris is also 51.85° north of due west.
Map image - Roger Hedin
Dendera was dedicated to Isis/Sirius. The ancient Egyptian year began on the date of the heliacal rising of Sirius in mid July. The helical rising of Sirius heralded the annual inundation of the Nile that was essential to the welfare of ancient Egypt. The axis of the temple of Isis at Dendera was aligned 20° south of due east, pointing directly at the rising point of Sirius from the latitude of Dendera.
Robert Bauval describes a number of connections between Isis/Sirius and Paris in Talisman (2004). Isis is shown riding on a boat in many ancient Egyptian drawings and carvings. At the direction of Napoleon, Sirius and a statue of Isis were added to the coat of arms for Paris shown below.

During the French revolution, a statue of Isis known as the Fountain of Regeneration was constructed on the former site of the Bastille. The engraving below commemorated this statue.

Fountain of Regeneration Engraving
The Elysian Fields is described as a place of eternal salvation in the ancient Egyptian Book of the Dead. Named after the Elysian Fields, the Champs Elysees is the main axis of Paris. The names Elysian and Elysees both suggest an association with Isis. The photograph below is facing southeast. The Arc de Triumphe is visible in the background. Beyond the Arc de Triumphe is the Louvre. The azimuth of the Champs Elysees is 26° south of due east, pointing directly at the rising point of Sirius/Isis from the latitude of Paris.

The termination point of the Champs Elysees to the northwest is the Grande Arche, in the foreground of the picture above. The axis of the Grande Arche is offset 6.33° south of the axis of the Champs Elysees. With an azimuth of just over 32° south of due east, the azimuth of the axis of the Grande Arche is the same as the azimuth of the great circle alignment from Paris to Dendera.
The Grande Arche is a nearly perfect cube with a height of 110 meters, a width of 108 meters and a depth of 112 meters. It is often described as a cube with side lengths of 110 meters. This is equal to 210 ancient Egyptian cubits:
110/210 = .5238
.5238 meters is a precise measure of the ancient Egyptian cubit, equating to 20.6222 inches, well within the ± .005 inches in Petrie's 20.62 inch measure of the ancient Egyptian cubit. Instead of the usual comparisons between the cubit and the meter of .52375/1 or .524/1, the best comparative measure may be the simple fraction of 11/21 that is suggested by the Grande Arche.

Image © Insecula.com
The sides of the Grande Arche are divided into 5 x 5 large panels and within each large panel are 7 x 7 smaller panels. Side lengths of 110 meters suggest lengths of 22 meters for the sides of the large panels with lengths of 22/7 meters for the sides of the smaller panels. The fraction 22/7 equals 3.1428, an accurate expression of π that is also found in the dimensions of the Great Pyramid. Side lengths of 210 cubits in the Grande Arche suggest lengths of 42 cubits for the sides of the large panels and 6 cubits for the sides of the smaller panels. This also shows that the relationship between the meter and the cubit is 6/π, using the measure of 22/7 for π:
21/11 = 6/π
22/7 x 21/11 = 6

The northern pyramid at Dashur, known as the Red Pyramid, was the first true (smooth sided) pyramid built in Egypt and it was the last pyramid built prior to construction of the Great Pyramid. The baselengths of the Red Pyramid are 420 cubits (220 meters) long, 20x multiples of 21/11.

Image by Jon Bodsworth
One of the oldest stone circles in England is at Rollright. The diameter of the Rollright circle is 31.4 meters, an accurate expression of π times 10 meters. Given the 6/π relationship between the meter and the cubit, the diameter of the Rollright circle is also 60 ancient Egyptian cubits.

BACK
http://home.hiwaay.net/~jalison/Art5.html

