Fibonacci 24 Repeating Pattern
May 15, 2012 by Gary Meisner
The Fibonacci sequence has a pattern that repeats every 24 numbers.
Numeric reduction is a technique used in analysis of numbers in which all the digits of a number are added together until only one digit remains. As an example, the numeric reduction of 256 is 4 because 2+5+6=13 and 1+3=4.
Applying numeric reduction to the Fibonacci series produces an infinite series of 24 repeating digits:
1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9
If you take the first 12 digits and add them to the second twelve digits and apply numeric reduction to the result, you find that they all have a value of 9.
| 1st 12 numbers |
1 |
1 |
2 |
3 |
5 |
8 |
4 |
3 |
7 |
1 |
8 |
9 |
| 2nd 12 numbers |
8 |
8 |
7 |
6 |
4 |
1 |
5 |
6 |
2 |
8 |
1 |
9 |
| Numeric reduction – Add rows 1 and 2 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
18 |
| Final numeric reduction – Add digits of result |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
This pattern was contributed both by Joseph Turbeville and then again by a mathematician by the name of Jain.
We would expect a pattern to exist in the Fibonacci series since each number in the series encodes the sum of the previous two. What’s not quite so obvious is why this pattern should repeat every 24 numbers or why the first and last half of the series should all add to 9.
For those of you from the “Show Me” state, this pattern of 24 digits is demonstrated in the numeric reduction of the first 73 numbers of the Fibonacci series, as shown below:
|
Fibonacci Number
|
Numeric reduction by adding digits |
| 1st Level |
2nd Level |
Final Level |
| Example: 2,584 |
2+5+8+4=19 |
1+9=10 |
1+0=1 |
| 0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
| 2 |
2 |
2 |
2 |
| 3 |
3 |
3 |
3 |
| 5 |
5 |
5 |
5 |
| 8 |
8 |
8 |
8 |
| 13 |
4 |
4 |
4 |
| 21 |
3 |
3 |
3 |
| 34 |
7 |
7 |
7 |
| 55 |
10 |
1 |
1 |
| 89 |
17 |
8 |
8 |
| 144 |
9 |
9 |
9 |
| 233 |
8 |
8 |
8 |
| 377 |
17 |
8 |
8 |
| 610 |
7 |
7 |
7 |
| 987 |
24 |
6 |
6 |
| 1,597 |
22 |
4 |
4 |
| 2,584 |
19 |
10 |
1 |
| 4,181 |
14 |
5 |
5 |
| 6,765 |
24 |
6 |
6 |
| 10,946 |
20 |
2 |
2 |
| 17,711 |
17 |
8 |
8 |
| 28,657 |
28 |
10 |
1 |
| 46,368 |
27 |
9 |
9 |
| 75,025 |
19 |
10 |
1 |
| 121,393 |
19 |
10 |
1 |
| 196,418 |
29 |
11 |
2 |
| 317,811 |
21 |
3 |
3 |
| 514,229 |
23 |
5 |
5 |
| 832,040 |
17 |
8 |
8 |
| 1,346,269 |
31 |
4 |
4 |
| 2,178,309 |
30 |
3 |
3 |
| 3,524,578 |
34 |
7 |
7 |
| 5,702,887 |
37 |
10 |
1 |
| 9,227,465 |
35 |
8 |
8 |
| 14,930,352 |
27 |
9 |
9 |
| 24,157,817 |
35 |
8 |
8 |
| 39,088,169 |
44 |
8 |
8 |
| 63,245,986 |
43 |
7 |
7 |
| 102,334,155 |
24 |
6 |
6 |
| 165,580,141 |
31 |
4 |
4 |
| 267,914,296 |
46 |
10 |
1 |
| 433,494,437 |
41 |
5 |
5 |
| 701,408,733 |
33 |
6 |
6 |
| 1,134,903,170 |
29 |
11 |
2 |
| 1,836,311,903 |
35 |
8 |
8 |
| 2,971,215,073 |
37 |
10 |
1 |
| 4,807,526,976 |
54 |
9 |
9 |
| 7,778,742,049 |
55 |
10 |
1 |
| 12,586,269,025 |
46 |
10 |
1 |
| 20,365,011,074 |
29 |
11 |
2 |
| 32,951,280,099 |
48 |
12 |
3 |
| 53,316,291,173 |
41 |
5 |
5 |
| 86,267,571,272 |
53 |
8 |
8 |
| 139,583,862,445 |
58 |
13 |
4 |
| 225,851,433,717 |
48 |
12 |
3 |
| 365,435,296,162 |
52 |
7 |
7 |
| 591,286,729,879 |
73 |
10 |
1 |
| 956,722,026,041 |
44 |
8 |
8 |
| 1,548,008,755,920 |
54 |
9 |
9 |
| 2,504,730,781,961 |
53 |
8 |
8 |
| 4,052,739,537,881 |
62 |
8 |
8 |
| 6,557,470,319,842 |
61 |
7 |
7 |
| 10,610,209,857,723 |
51 |
6 |
6 |
| 17,167,680,177,565 |
67 |
13 |
4 |
| 27,777,890,035,288 |
73 |
10 |
1 |
| 44,945,570,212,853 |
59 |
14 |
5 |
| 72,723,460,248,141 |
51 |
6 |
6 |
| 117,669,030,460,994 |
65 |
11 |
2 |
| 190,392,490,709,135 |
62 |
8 |
8 |
| 308,061,521,170,129 |
46 |
10 |
1 |
| 498,454,011,879,264 |
72 |
9 |
9 |
Thanks to Joseph Turbeville for sending “A Glimmer of Light from the Eye of a Giant” and to Helga Hertsig for bringing Jain’s discovery of this pattern to my attention.
Filed Under: Math
https://www.goldennumber.net/fibonacci-24-pattern/ |
|
|
 Primer Primer  Anterior 2 a 3 de 3 Siguiente Anterior 2 a 3 de 3 Siguiente  Último Último  |
|
|
Fibonacci 60 Repeating Pattern
October 30, 2016 by Gary Meisner
The last digit of the numbers in the Fibonacci Sequence form a pattern that repeats after every 60th number:
0, 1, 1, 2, 3, 5, 8, 3, 1, 4, 5, 9, 4, 3, 7, 0, 7, 7, 4, 1, 5, 6, 1, 7, 8, 5, 3, 8, 1, 9, 0, 9, 9, 8, 7, 5, 2, 7, 9, 6, 5, 1, 6, 7, 3, 0, 3, 3, 6, 9, 5, 4, 9, 3, 2, 5, 7, 2, 9, 1
This pattern can be seen in the following list of the first 72 Fibonacci numbers:
| 0 |
0 |
| 1 |
1 |
| 2 |
1 |
| 3 |
2 |
| 4 |
3 |
| 5 |
5 |
| 6 |
8 |
| 7 |
13 |
| 8 |
21 |
| 9 |
34 |
| 10 |
55 |
| 11 |
89 |
| 12 |
144 |
| 13 |
233 |
| 14 |
377 |
| 15 |
610 |
| 16 |
987 |
| 17 |
1,597 |
| 18 |
2,584 |
| 19 |
4,181 |
| 20 |
6,765 |
| 21 |
10,946 |
| 22 |
17,711 |
| 23 |
28,657 |
| 24 |
46,368 |
| 25 |
75,025 |
| 26 |
121,393 |
| 27 |
196,418 |
| 28 |
317,811 |
| 29 |
514,229 |
| 30 |
832,040 |
| 31 |
1,346,269 |
| 32 |
2,178,309 |
| 33 |
3,524,578 |
| 34 |
5,702,887 |
| 35 |
9,227,465 |
| 36 |
14,930,352 |
| 37 |
24,157,817 |
| 38 |
39,088,169 |
| 39 |
63,245,986 |
| 40 |
102,334,155 |
| 41 |
165,580,141 |
| 42 |
267,914,296 |
| 43 |
433,494,437 |
| 44 |
701,408,733 |
| 45 |
1,134,903,170 |
| 46 |
1,836,311,903 |
| 47 |
2,971,215,073 |
| 48 |
4,807,526,976 |
| 49 |
7,778,742,049 |
| 50 |
12,586,269,025 |
| 51 |
20,365,011,074 |
| 52 |
32,951,280,099 |
| 53 |
53,316,291,173 |
| 54 |
86,267,571,272 |
| 55 |
139,583,862,445 |
| 56 |
225,851,433,717 |
| 57 |
365,435,296,162 |
| 58 |
591,286,729,879 |
| 59 |
956,722,026,041 |
| 60 |
1,548,008,755,920 |
| 61 |
2,504,730,781,961 |
| 62 |
4,052,739,537,881 |
| 63 |
6,557,470,319,842 |
| 64 |
10,610,209,857,723 |
| 65 |
17,167,680,177,565 |
| 66 |
27,777,890,035,288 |
| 67 |
44,945,570,212,853 |
| 68 |
72,723,460,248,141 |
| 69 |
117,669,030,460,994 |
| 70 |
190,392,490,709,135 |
| 71 |
308,061,521,170,129 |
| 72 |
498,454,011,879,264 |
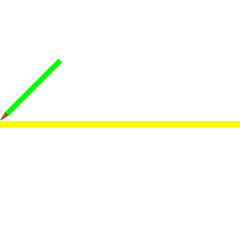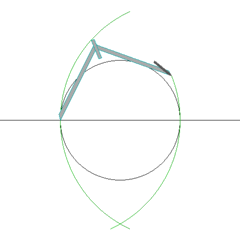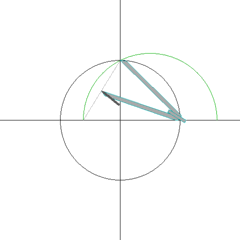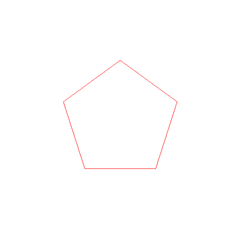
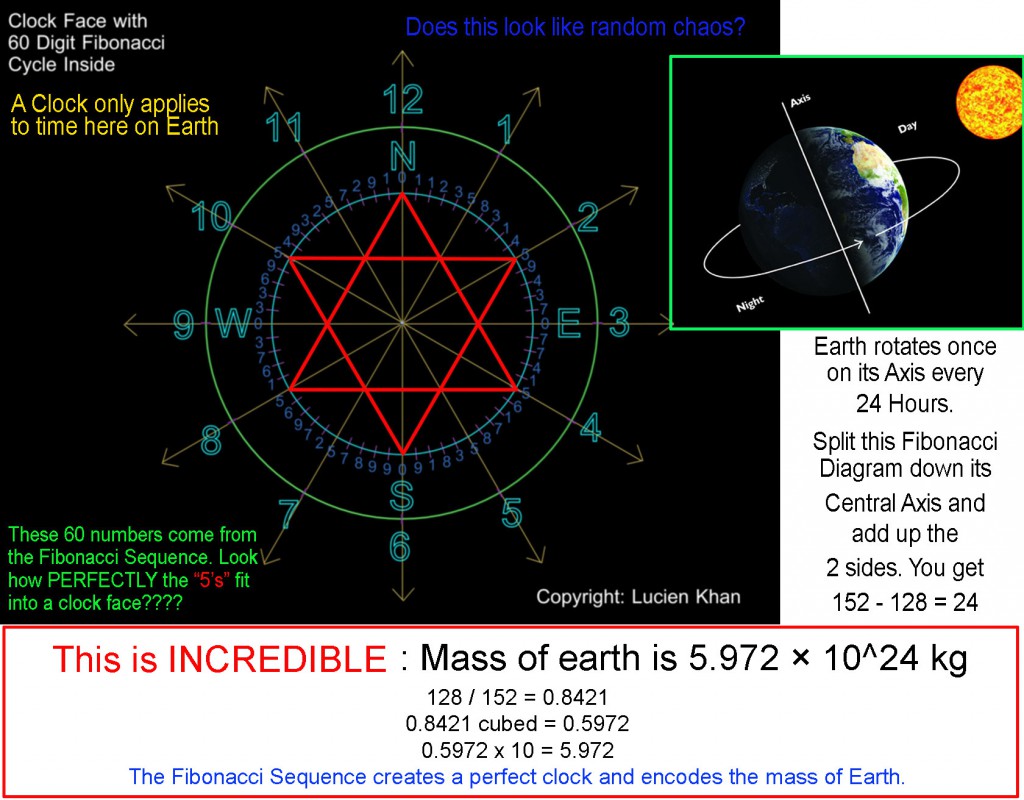
Lucien Khan arranged these 60 digits of the pattern in a circle, as shown in illustration below:
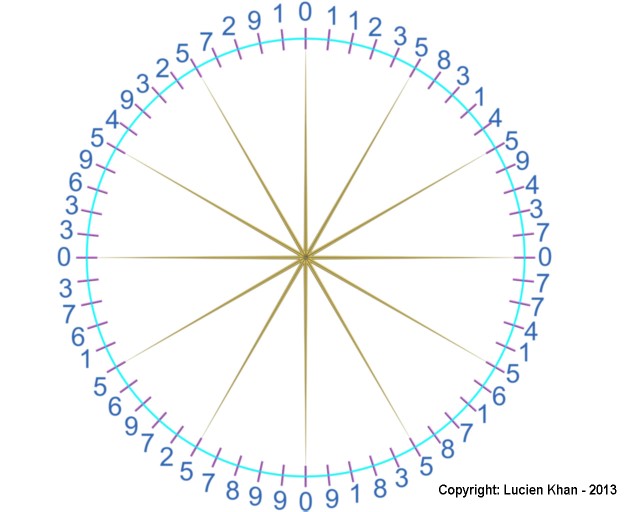
Here he found other interesting results:
- The zeros align with the 4 cardinal points on a compass.
- The fives align with the 8 other points of the 12 points on a clock.
- Except for the zeros, the number directly opposite each number adds to 10.
Lucien postulates that ancient knowledge of these relationships contributed to the development of our modern use of 60 minutes in an hour, and presentation of numbers on the face of the clock.
I found too that any group of four numbers that are 90 degrees from each other (15 away from each other in the circle) sum to 20, except again for the zeros. As an example, use 1, 7, 9 and 3, which appear one to the right of each of the compass points.
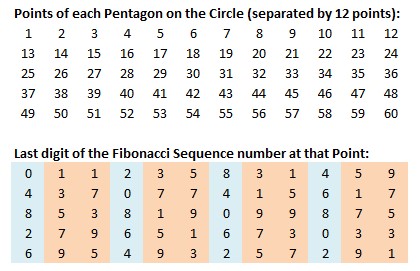
Additionally, every group of five numbers that define the points of the 12 pentagons on the circle also create a pattern. Four of the pentagons have even-numbered last digits of 0, 2, 4, 6, and 8. The remaining eight pentagons have odd-numbered last digits of 1, 3, 5, 7 and 9.
Another interesting pattern yet was observed by Lucien Khan: The 216th number is this sequence is 619220451666590135228675387863297874269396512. The sum of all the digits in that number add up to 216, as well. He notes that it is believed that the secret or hidden name of God contains 216 characters. There are many other fascinating relationships and sacred geometries, which are presented by Lucien Khan in more detail at the links below.
https://www.goldennumber.net/fibonacci-60-repeating-pattern/ |
|
|
|