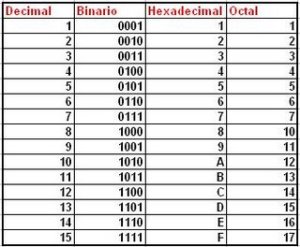
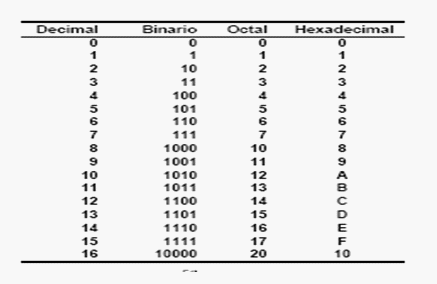
Los sistemas de numeración son conjuntos de dígitos usados para representar cantidades, así se tienen los sistemas de numeración decimal, binario, octal, hexadecimal, romano, etc. Los cuatro primeros se caracterizan por tener una base (número de dígitos diferentes: diez, dos, ocho, dieciseis respectivamente) mientras que el sistema romano no posee base y resulta más complicado su manejo tanto con números, así como en las operaciones básicas.
Los sistemas de numeración que poseen una base tienen la característica de cumplir con la notación posicional, es decir, la posición de cada número le da un valor o peso, así el primer dígito de derecha a izquierda después del punto decimal, tiene un valor igual a b veces el valor del dígito, y así el dígito tiene en la posición n un valor igual a: (bn) * A
donde:
b = valor de la base del sistema
n = número del dígito o posición del mismo
A = dígito.
- Sistema binario:
El sistema de numeración más simple que usa la notación posicional es el sistema de numeración binario. Este sistema, como su nombre lo indica, usa solamente dos dígitos (0,1). Por su simplicidad y por poseer únicamente dos dígitos diferentes, el sistema de numeración binario se usa en computación para el manejo de datos e información.
A la representación de un dígito binario se le llama bit y al conjunto de 8 bits se le llama byte, así por ejemplo: 110 contiene 3 bits, 1001 contiene 4 y 1 contiene 1 bit.
Como el sistema binario usa la notación posicional entonces el valor de cada dígito depende de la posición que tiene en el número, así por ejemplo el número 110101b es:
- Sistema octal:
El sistema de numeración octal es también muy usado en la computación por tener una base que es potencia exacta de 2 o de la numeración binaria. Esta característica hace que la conversión a binario o viceversa sea bastante simple. El sistema octal usa 8 dígitos (0,1,2,3,4,5,6,7) y tienen el mismo valor que en el sistema de numeración decimal. Como el sistema de numeración octal usa la notación posicional entonces para el número 3452.32q tenemos:
2*(80) + 5*(81) + 4*(82) + 3*(83) + 3*(8-1) + 2*(8-2) = 2 + 40 + 4*64 + 64 + 3*512 + 3*0.125 + 2*0.015625 = 2 + 40 + 256 + 1536 + 0.375 + 0.03125 = 1834 + 40625d entonces, 3452.32q = 1834.40625d
- Sistema decimal:
El sistema de numeración decimal es el más usado, tiene como base el número 10, o sea que posee 10 dígitos diferentes (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). El sistema de numeración decimal fué desarrollado por los hindúes, posteriormente lo introducen los árabes en Europa, donde recibe el nombre de sistema de numeración decimal o arábigo. Si se aplica la notación posicional al sistema de numeración decimal entonces el dígito número n tiene el valor: (10n)* A
Este valor es positivo y es mayor o igual que uno si el dígito se localiza a la izquierda del punto decimal y depende del dígito A, en cambio el valor es menor que uno si el dígito se localiza a la derecha del punto decimal.
- Sistema hexadecimal:
Un gran problema con el sistema binario es la verbosidad. El sistema de numeración hexadecimal, o sea de base 16, resuelve este problema (es común abreviar hexadecimal como hex aunque hex significa base seis y no base dieciseis). El sistema hexadecimal es compacto y nos proporciona un mecanismo sencillo de conversión hacia el formato binario, debido a ésto, la mayoría del equipo de cómputo actual utiliza el sistema numérico hexadecimal. Como la base del sistema hexadecimal es 16, cada dígito a la izquierda del punto hexadecimal representa tantas veces un valor sucesivo potencia de 16, por ejemplo, el número 123416 es igual a:
lo que da como resultado:
4096 + 512 + 48 + 4 = 466010
Cada dígito hexadecimal puede representar uno de dieciseis valores entre 0 y 1510. Como sólo tenemos diez dígitos decimales, necesitamos inventar seis dígitos adicionales para representar los valores entre 1010 y 1510. En lugar de crear nuevos símbolos para estos dígitos, utilizamos las letras A a la F.



















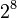 valores posibles, y esto puede representarse como
valores posibles, y esto puede representarse como 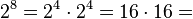
 , que equivale al número en base 16
, que equivale al número en base 16 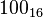 , dos dígitos hexadecimales corresponden exactamente a un byte.
, dos dígitos hexadecimales corresponden exactamente a un byte.