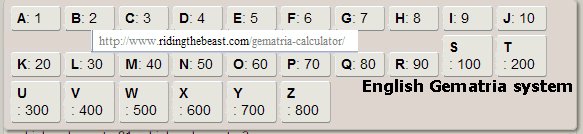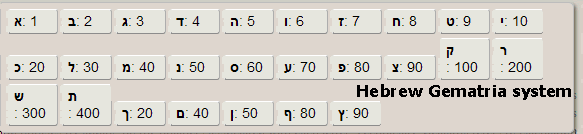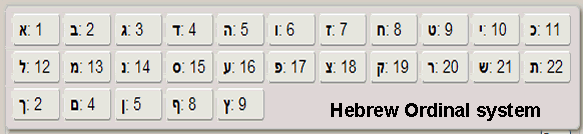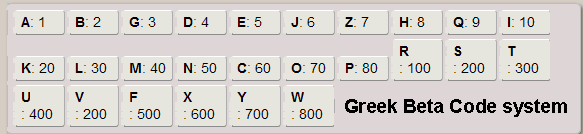
Aside from you chronically late people, we all know how time works:
This system is okay. But also, it’s kind of crazy.
Why 60 minutes per hour? Why 60 seconds per minute? It goes back to Babylon, with their base 60 number system—the same heritage that gives us 360 degrees in a circle. Now, that’s all well and good for Babylon 5 fans, but our society isn’t base-60. It’s base-10. Shouldn’t our system of measuring time reflect that?
So ring the bells, beat the drums, and summon the presidential candidates to “weigh in,” because I hereby give you… metric time.
Now, this represents a bit of a change. The new seconds are a bit shorter. The new minutes are a bit longer. And the new hours are quite different—nearly two and a half times as long.
So why do this? Because it’d be so much easier to talk about time!
Here’s one improvement: analog clocks are easier to read. At first glance, the improvement may not be so obvious—we’ve simply reshuffled the numbers a bit.
But notice, the minute hand makes more sense now. When it’s at the 2, we’re 20 minutes past the hour. When it’s at the 7, we’re 70 minutes after the hour. And so on.
Second, times are no longer duplicated. For example, instead of needing to distinguish between 6am and 6pm, we can simply say “2:50” and “7:50.” (This is, of course, how “military time” currently works.)
Third—this is a big one—the time tells you how far through the day you are. The time 2:00 is exactly 20% of the way through the day. At 8:76, we’re exactly 87.6% of the way through the day.
Fourth, consider the moment when we’re 99.9% of the way through the day. In the new metric system, we get to watch the clock roll from 9:99 back around to 0:00. Isn’t that nicer and more conclusive than 11:59pm rolling around to 12:00am?
Fifth, it’s so much easier to talk about longer times. Two and a half days? That’s 25 hours. Three days and 6 hours? That’s simply 3.6 days. Since an hour is now a nice decimal fraction of a day, these conversions become easy.
Will there be adjustments to make? Certainly! But the adjustments are half of the fun.
Let’s start, as all good things do, with television. Whether you enjoy half-hour sitcoms or hour-long dramas, the length of your favorite shows is probably going to change. Why? Because, under our new system, what we now call “half an hour” will be 20.83 minutes. What we now call “an hour” will be 41.67.
There’s nothing magical about these “half-hour” and “hour” lengths, obviously. They were chosen simply because they were nice round numbers. But under the new system, they aren’t! Since it’d be silly to divide the TV schedule into 21-minute intervals, presumably television networks would tweak the lengths to go more evenly into an hour.
If so, they’d have two choices: 5 blocks per hour (i.e., two dramas, plus a sitcom), or 4 blocks per hour (i.e., two dramas).
If you choose the former, shows will be 4% shorter than today, leading to accelerated storytelling. (It’s the same change that’s unfolded over the last 20 years, as increased ad time has squeezed the shows themselves to be shorter.)
And if you choose the latter, shows will be 20% longer. They’ll perhaps unfold at a slower, more cinematic speed. Either way, expect the pacing and rhythm of TV shows to change.
Sports run into the same issue. Football will probably opt for four quarters of 10 minutes each, which shortens the game by 4%. Expect slightly diminished scoring as a result. (And, if we’re lucky, diminished concussions.)
Hockey, meanwhile, might go for three periods of 15 minutes each, which actually makes the game 8% longer. It might give someone a chance to tackle Wayne Gretzky’s scoring records (but then again, probably not—he’s way out of reach right now).
I’d expect soccer to select two halves of 30 minutes each, which (as with American football) shortens games by 4%. If you thought soccer was too high-scoring already, you’re in luck (and also in a very small minority, I suspect).
When it comes to sports, the lengths of games won’t be the only thing changing. We also need to reconsider record running times.
Usain Bolt’s world-record for the 100-meter dash (currently 9.58 seconds) would be, under the new system, 11.09 metric seconds. Doing the 100m in 11 metric seconds might be achievable in the future, but 10 seconds? Perhaps never. (That’s the equivalent of 8.64 of our seconds!)
What about the mile? Well, it’s a little funny to imagine a world with metric time still worrying about that strange unit of distance (5280 feet? Really?), but the famed 4-minute mile would correspond to a 2.78-minute mile.
This is weird because, for top runners in the 1940s and 1950s, the barrier to running a 4-minute mile may have been less physiological than psychological. Would the 2.8-minute mile have felt as intimidating? Would the 3-minute mile? Perhaps it’d be the 2.5-minute mile, seeing as the current world record (3:43 in our old system) is 2.58 metric minutes?
And we might as well mention the marathon, where the world record time (currently 2:02:57) is now under an hour: 85 minutes, 38 seconds. I suspect that the 1-hour marathon would be a real badge of honor, something that every distance runner aspires to.
Leaving sports aside, what about food?
Restaurants would open for breakfast at perhaps 3:00 or 3:50. (Of course, coffee shops like Starbucks might open as early as 2:50.)
You’d get lunch around 5:00—that is to say, noon. Under our current system, I feel silly eating before 11:30, which is 4:80 under the new system. But I wonder—would I feel comfortable grabbing lunch at 4:75? Perhaps even 4:60 (even though that’s earlier than 11am under our current scheme)?
Eating is psychological, and how we number our hours might steer our behavior.
As for dinner, I suspect 7:50 to 8:00 would be the preferred time (although the famously late-eating Spaniards might hold off until 8:75 or 9:00).
Other numbers change, too. Take speed limits: the typical 65mph limit on many highways translates to 156 mph under the new system; I suspect we’d see that bumped up to 160 mph or down to 150 mph for the sake of roundness (which translates to 66.7mph or 62.5mph under our current system).
The speed of sound? Not 340 meters per second any longer; it’s now just 294 meters per second. Meters haven’t changed, of course, but seconds have gotten shorter!
And the speed of light? Unfortunately, we lose the lovely number 300 million meters per second; instead, it becomes roughly 260 million meters per second.
Speaking of light, on the equinox, you get 5 hours of light and 5 hours of dark.
The winter solstice is pretty grim: in London, you’d see just 3 hours, 25 minutes, and 25 seconds of daylight.
The summer solstice is nice, though: London would get 6 hours, 93 minutes of sun.
Okay, time to come clean: I propose this without a single iota of seriousness. It’d be insane to ditch our current system. We’re used to it. We’ve agreed upon it. We’ve built our lives around it. The hassle of a change far outweighs the gains.
But I still love the thought experiment. It asks you, in some small way, to reimagine your life. How do you spend your time? How do you measure the success of a day? When you plan your hours, are you conceding to the arbitrary dictates of a quirky clock, or are you truly giving your tasks the time that they deserve? If I scrambled your sense of time, relabeling all your moments, would it change the way you feel about them? Do the numbers we assign to times matter? Or are we just scratching lines on the shifting dunes of eternity?




.jpg)