|
|
El Gato de Schrödinger - Mención en The Big Bang Theory
 La paradoja de Schrödinger
El gato de Schrödinger es la paradoja más popular de la cuántica. La propuso el nobel austríaco Erwin Schrödinger en 1935. Es un experimento mental que muestra lo desconcertante del mundo cuántico. Tiene distintas variantes, exponemos la más sencilla.
Erwin Schrödinger
Imaginemos un gato dentro de una caja completamente opaca. En su interior se instala un mecanismo que une un detector de electrones a un martillo. Y, justo debajo del martillo, un frasco de cristal con una dosis de veneno letal para el gato. Si el detector capta un electrón activará el mecanismo, haciendo que el martillo caiga y rompa el frasco.
Se dispara un electrón. Por lógica, pueden suceder dos cosas. Puede que el detector capte el electrón y active el mecanismo. En ese caso, el martillo cae, rompe el frasco y el veneno se expande por el interior de la caja. El gato lo inhala y muere. Al abrir la caja, encontraremos al gato muerto. O puede que el electrón tome otro camino y el detector no lo capte, con lo que el mecanismo nunca se activará, el frasco no se romperá, y el gato seguirá vivo. En este caso, al abrir la caja el gato aparecerá sano y salvo.
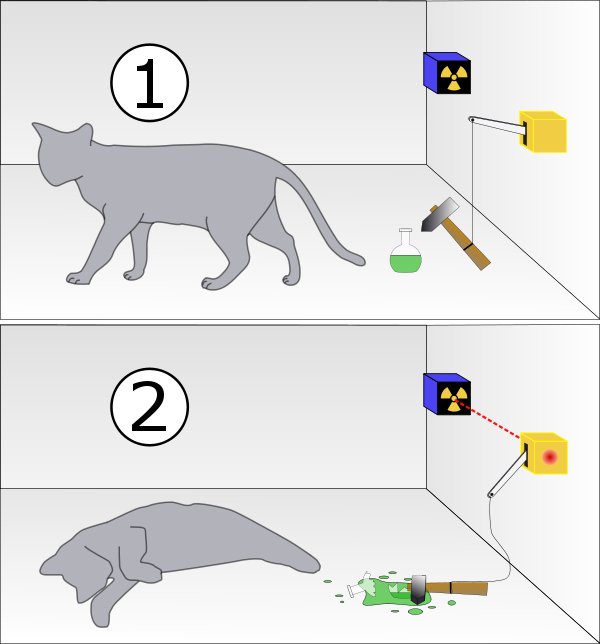
Hasta aquí todo es lógico. Al finalizar el experimento veremos al gato vivo o muerto. Y hay un 50% de probabilidades de que suceda una cosa o la otra. Pero la cuántica desafía nuestro sentido común.
El electrón es al mismo tiempo onda y partícula. Para entenderlo, sale disparado como una bala, pero también, y al mismo tiempo, como una ola o como las ondas que se forman en un charco cuando tiramos una piedra. Es decir, toma distintos caminos a la vez. Y además no se excluyen sino que se superponen, como se superpondrían las ondas de agua en el charco. De modo que toma el camino del detector y, al mismo tiempo, el contrario. El electrón será detectado y el gato morirá. Y, al mismo tiempo, no será detectado y el gato seguirá vivo. A escala atómica, ambas probabilidades se cumplen. En el mundo cuántico, el gato acaba vivo y muerto a la vez, y ambos estados son igual de reales. Pero, al abrir la caja, nosotros sólo lo vemos vivo o muerto.
¿Qué ha ocurrido? Si ambas posibilidades se cumplen y son reales, ¿por qué sólo vemos una? La explicación es que el experimento aplica las leyes cuánticas, pero el gato no es un sistema cuántico. La cuántica actúa a escala subatómica y sólo bajo determinadas condiciones. Sólo es válida en partículas aisladas. Cualquier interacción con el entorno hace que las leyes cuánticas dejen de aplicarse.
Muchas partículas juntas interactúan entre sí, por eso la cuántica no vale en el mundo de lo grande, como el gato. Tampoco cuando hay calor, pues el calor es el movimiento de los átomos interactuando. Y el gato es materia caliente. Pero lo más sorprendente es que incluso nosotros, al abrir la caja y observar el resultado del experimento, interactuamos y lo contaminamos.
Así es. Una curiosa característica de la cuántica es que el mero hecho de observar contamina el experimento y define una realidad frente a las demás. Einstein expresaba así su desconcierto: "¿quiere esto decir que la Luna no está ahí cuando nadie la mira?"
Conclusión: cuando el sistema cuántico se rompe, la realidad se define por una de las opciones. Sólo veremos al gato vivo o muerto, nunca ambas. Este proceso de tránsito de la realidad cuántica a nuestra realidad clásica se llama decoherencia, y es la responsable de que veamos el mundo tal y como lo conocemos. Es decir, una única realidad. ¿El motivo de este Post? Es el siguiente:
Mención en The Big Bang Theory
En el final de la Primera Temporada, Leonard finalmente reúne el coraje suficiente para invitar a Penny a salir. Penny no está acostumbrada a salir con tipos como Leonard y eso pudo ocasionar que sus relaciones anteriores no hayan funcionado, pero por otro lado si esta relación no termina bien, se arriesgaría a perder un buen amigo.
Penny le pide algún consejo a Sheldon porque debería conocer a Leonard más que al resto. Sheldon le da la solución de considerar al gato de Schrodinger.
Penny confunde Schrodinger con la vecina del apartamento 2A pero Sheldon la corrige de inmediato diciéndole que esa es la Señorita Grossinger, y le comienza a explicar que en 1935, Erwin Schrödinger, en un intento de explicar la interpretación de la física cuántica de Copenhague, propuso un experimento donde un gato es situado dentro de una caja con conductos de veneno que serian abiertos en un momento aleatorio y como nadie sabe cuándo o si el veneno se ha introducido, hasta que la caja se abriese, el gato puede ser considerado tanto vivo como muerto.
Penny no entendió la explicación y Sheldon le responde que eso es porque aun no terminaba de explicar. Sheldon continua diciendo que simplemente el gato de Schrodinger es la potencial relación que tiene ella con Leonard ahora mismo, puede ser pensada tanto como mala y como buena, y que solo abriendo la caja se puede averiguar cuál es.
Penny cree entender lo que trata de decir Sheldon. Ella debe salir con Leonard, Pero Sheldon le responde que eso no era lo que quería decir, y comienza a explicarle el experimento del gato de Schrödinger todo de nuevo.
En el día de la cita, Leonard va a buscar a Penny y estos dos se demostraban muy nerviosos. Penny le dice que antes de salir deberían hablar pero Leonard le pregunta antes si conocía sobre el gato de Schrodinger. Penny le responde que conoce demasiado sobre ese gato por lo que Leonard la besa sorpresivamente. Al terminar, Penny concluye que la relación podía funcionar 
|
|
|
|
|
11 DE SEPTIEMBRE O SEPTIEMBRE 11
11/9 O 9/11
Sapientia Aedificavit Sibi Domum. Es decir, "la sabiduría ha edificado aquí su casa". Resulta curioso que la misma frase aparece en el Evangelio de María Magdalena, un texto apócrifo. Se dice que en el interior de esta iglesia y de otras muchas de Venecia está escondido el tesoro de los templarios. Pero no hay ninguna prueba de ello. Para terminar ya con esta entrada me gustaría que nos acercásemos un momento a uno de los edificios más emblemáticos de Venecia: el Palacio Ducal.
La Maddalena
La Maddalena
ISLA SAN GIORGIO (VENECIA)=GEORGE LEMAITRE
GEMATRIA EN INGLES DE SEED=33
GEMATRIA EN INGLES DE GATE=33
SARA (CE-SAREA DE FILIPO)=PARALELO 33
"¡Oh profundidad de las riquezas de la sabiduría (sophia)
y de la ciencia (gnwsiV, gnosis) de Dios!
¡Cuán incomprensibles son sus juicios, e inescrutables sus caminos!"
(Romanos, 11: 33).
 the Apple
| milky way in Simple Gematria Equals: 119 |
( |
m 13 |
i9 |
l 12 |
k 11 |
y 25 |
0 |
w 23 |
a1 |
y 25 |
) |
| queen mary in Simple Gematria Equals: 119 |
( |
q 17 |
u 21 |
e5 |
e5 |
n 14 |
0 |
m 13 |
a1 |
r 18 |
y 25 |
|
| hebrew calendar in Simple Gematria Equals: 119 |
( |
h8 |
e5 |
b2 |
r 18 |
e5 |
w 23 |
0 |
c3 |
a1 |
l 12 |
e5 |
n 14 |
d4 |
a1 |
r 18 |
| mary magdalene in Simple Gematria Equals: 119 |
( |
m 13 |
a1 |
r 18 |
y 25 |
0 |
m 13 |
a1 |
g7 |
d4 |
a1 |
l 12 |
e5 |
n 14 |
e5 |
|
|
|
|
|
|
BENJAMIN/LOBO/PERRO/GUERRA/MARTE/HORUS
EN ESTE VERSICULO ESTA LA CLAVE DE LOS VIAJES EN EL TIEMPO
|
|
|
|
|
Sabemos que Vesica Piscis esta en funcion al a los 153 peces de Juan 21:11.
 Aqui tenemos a Pi - la circunferencia del toro y la vesica piscis 256/153 equivalente a la raiz cuadrada de 3 En el hipercubo las coordinadas binarias de Piscis son decimal 3 y binario 11 153 los pescados de Jesus en la biblia   
I have a lot to say about pythagorean triangles in my videos. In particular I have found many references to 5:12:13 triangles and 5:12 rectangles (that’s 2 of the triangles put together) in Stonehenge and the whole region surrounding it, in Washington DC, Paris, and Jerusalem. Someone who listened to my first Red Ice interview contacted me with a major discovery he made in regards to the 5:12 proportion. Brace yourself…
A rectangle measuring 5 feet by 12 feet has an area of 8640 square inches. This is something I can work with. I’m never going to be able to build an 864 foot solar Osiris talisman on a geodetic hot spot, but I think I can manage making a few raised garden beds measuring exactly 5 by 12 feet. And where I live in Canada (above 50 degrees North) can really use more resonance with the Sun.
If you saw SIPS Volume 1, you might recall that Stonehenge has its station stones which describe a 5×12 rectangle.
from SIPS Volume 1
Stonehenge is also 33.33° from Solomon’s Temple.
 
Sapientia Aedificavit Sibi Domum. Es decir, "la sabiduría ha edificado aquí su casa". Resulta curioso que la misma frase aparece en el Evangelio de María Magdalena, un texto apócrifo. Se dice que en el interior de esta iglesia y de otras muchas de Venecia está escondido el tesoro de los templarios. Pero no hay ninguna prueba de ello. Para terminar ya con esta entrada me gustaría que nos acercásemos un momento a uno de los edificios más emblemáticos de Venecia: el Palacio Ducal.
|
|
|
|
|
 
|
LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
Incendio Notre Dame: Última hora de la catedral de París (15 DE ABRIL)
 Incendio Notre Dame (París), en directo (Bertrand Guay / AFP)
PHI A NOTRE-DAME
A la catredal de Notre Dame hi observem més rectanlges auris: Creat per Mario Pastor 
The DaVinci Code, Notre Dame Cathedral from DaVinci Code
original movie prop
HEXAGONO=OCTAHEDRO =ESTRELLA DE 6 PUNTAS= SATURNO =CUBO/HEXAGONO= ESPACIO/TIEMPO =1 DE REYES 6:20 Y APOCALIPSIS 21:16
EL SEXTO DIA ES EL VIERNES Y EL OCTAVO EL DOMINGO. INCREIBLE
   
August 23, 2018/
The Golden Section (aka Golden Mean, and Golden Ratio) phys.org
We use math in architecture on a daily basis to solve problems. We use it to achieve both functional and aesthetic advantages. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance. As you will see from some of the examples below, the application of mathematical principles can result in beautiful and long-lasting architecture which has passed the test of time.
Using Math in Architecture for Function and Form
We use math in architecture every day at our office. For example, we use math to calculate the area of a building site or office space. Math helps us to determine the volume of gravel or soil that is needed to fill a hole. We rely on math when designing safe building structures and bridges by calculating loads and spans. Math also helps us to determine the best material to use for a structure, such as wood, concrete, or steel.
“Without mathematics there is no art.” – Luca Pacioli, De divina proportione, 1509
Architects also use math when making aesthetic decisions. For instance, we use numbers to achieve attractive proportion and harmony. This may seem counter-intuitive, but architects routinely apply a combination of math, science, and art to create attractive and functional structures. One example of this is when we use math to achieve harmony and proportion by applying a well-known principle called the Golden Section
Math and Proportion – The Golden Section
Perfect proportions of the human body – The Vitruvian Man – by Leonardo da Vinci.
We tend to think of beauty as purely subjective, but that is not necessarily the case. There is a relationship between math and beauty. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance.
The Golden Section is one example of a mathematical principle that is believed to result in pleasing proportions. It was mentioned in the works of the Greek mathematician Euclid, the father of geometry. Since the 4th century, artists and architects have applied the Golden Section to their work.
The Golden Section is a rectangular form that, when cut in half or doubled, results in the same proportion as the original form. The proportions are 1: the square root of 2 (1.414) It is one of many mathematical principles that architects use to bring beautiful proportion to their designs.
Examples of the Golden Section are found extensively in nature, including the human body. The influential author Vitruvius asserted that the best designs are based on the perfect proportions of the human body.
Over the years many well-known artists and architects, such as Leonardo da Vinci and Michelangelo, used the Golden Section to define the dimensions and proportions in their works. For example, you can see the Golden Section demonstrated in DaVinci’s painting Mona Lisa and his drawing Vitruvian Man.
Famous Buildings Influenced by Mathematical Principles
Here are some examples of famous buildings universally recognized for their beauty. We believe their architects used math and the principals of the Golden Section in their design:
Parthenon
The classical Doric columned Parthenon was built on the Acropolis between 447 and 432 BC. It was designed by the architects Iktinos and Kallikrates. The temple had two rooms to shelter a gold and ivory statue of the goddess Athena and her treasure. Visitors to the Parthenon viewed the statue and temple from the outside. The refined exterior is recognized for its proportional harmony which has influenced generations of designers. The pediment and frieze were decorated with sculpted scenes of Athena, the Gods, and heroes.
Parthenon Golden Section
Notre Dame Cathedral in Paris
Built on the Ile de la Cite, Notre Dame was built on the site of two earlier churches. The foundation stone was laid by Pope Alexander III in 1163. The stone building demonstrates various styles of architecture, due to the fact that construction occurred for over 300 years. It is predominantly French Gothic, but also has elements of Renaissance and Naturalism. The cathedral interior is 427 feet x 157 feet in plan. The two Gothic towers on the west façade are 223 feet high. They were intended to be crowned by spires, but the spires were never built. The cathedral is especially loved for its three stained glass rose windows and daring flying buttresses. During the Revolution, the building was extensively damaged and was saved from demolition by the emperor Napoleon.
Notre Dame Cathedral in Paris
Taj Mahal
Built in Agra between 1631 and 1648, the Taj Mahal is a white marble mausoleum designed by Ustad-Ahmad Lahori. This jewel of Indian architecture was built by Emperor Shah Jahan in memory of his favorite wife. Additional buildings and elements were completed in 1653. The square tomb is raised and is dramatically located at the end of a formal garden. On the interior, the tomb chamber is octagonal and is surrounded by hallways and four corner rooms. Building materials are brick and lime veneered with marble and sandstone.
Taj Mahal designed by Ustad-Ahmad Lahori
As you can see from the above examples, the application of mathematical principles can result in some pretty amazing architecture. The architects’ work reflects eye-catching harmony and balance. Although these buildings are all quite old, their designs have pleasing proportions which have truly passed the test of time.
https://bleckarchitects.com/math-in-architecture/
|
|
|
|
|
|
|
| Rolmen |
Enviado: 06/05/2019 19:01 |
|
Bariloche, estás enfermo de ira, de envidia, de egolatría, de odio, de soberbia, de frustración, necesitas ver un psicólogo o quizá mejor un psiquiatra y lo peor que tenés es que estás acomplejado, ignorás del mundo sin conocerlo, el valle del Silicón es la cuna de grandes industrias tecnológicas sita en el área de la Bahía de San Francisco en el norte del Estado de California y Netflix está localizado desde su fundación en Los Gatos, en el condado de Santa Clara, California, en el centro del Estado muy distante del valle del Silicón.
Con ello demostrás que sos un gil que solo posteás a lo boludo lo que te encontrás en internet, mejor deberías de quedarte callado y tratar de ser un poco inteligente.
Lo más triste es que todo lo relacionás, deberías de ir a una escuela nocturna para adultos y aprender geografía, física pero sobretodo, a no ser tan pelotudo.
Con todo respeto...es el marco ...
|
|
|
|
|
|
TODOS LOS CAMINOS CONDUCEN A ROMA
DE TERROR PARA LOS SANTURRONES FARISEOS QUE LES ENCANTA DEMONIZAR
|
|
|
|
|
|
|
| Te invitamos a conocer las oficinas de Netflix en Los Gatos, California. Videos Diario Financiero. Loading ...We have been visiting in Los Gatos with Netflix, which opened up for their daily locations where approx. 1000 ...
|
|
|
|
|
|
|
|
El Santo Grial y su posible localización en España
La leyenda indica que el Santo Grial fue el cáliz en que bebió Jesucristo durante la Última Cena, la cual le reunió con los doce apóstoles en las horas que precedieron a su muerte. Es, por tanto, una reliquia de enorme trascendencia para el cristianismo, seguramente una de las más valiosas. Actualmente no se sabe con certeza su paradero, aunque ciertas hipótesis apuntan a la posibilidad de que se encuentre en alguno de los templos cristianos de España. Los dos más representativos son los de la Colegiata de San Isidoro de León y la Catedral de Valencia. A continuación se relata la historia de estos dos Santos Cálices.
Santo Grial de la Colegiata de San Isidoro de León
Existen dos antiguos manuscritos egipcios de la Universidad de al-Azhar de El Cairo que relatan los hechos. El Santo Grial habría permanecido en una capilla de la iglesia del Santo Sepulcro de Jerusalén desde el siglo IV hasta inicios del siglo XI, cuando fue saqueada y el cáliz robado llegó hasta El Cairo. No se sabe nada de su ubicación antes del siglo IV.
En el año 1054 ocurrió que hubo una gran hambruna en Egipto. Desde el emirato musulmán de Denia se ayudó con el envío de víveres. Tras superar esta circunstancia, el califa fatimí de Egipto ofreció diversos regalos al emir de Denia como señal de agradecimiento. Uno de ellos fue el Santo Grial, parece que solicitado explícitamente por el emir de Denia, que se lo entregó al rey Fernando I de León, el monarca más poderoso de la época en la Península Ibérica, como gesto de confraternización entre los dos reinos, el cristiano y el musulmán.
Desde entonces permanece en León. Tras la muerte del rey Fernando I de León, la reliquia pasó a pertenecer a su hija la infanta Urraca de Zamora, que por expreso deseo mandó a los orfebres leoneses que fuese retocada para darla su aspecto actual. De hecho, es conocida como el Cáliz de Doña Urraca. En la actualidad se expone en el Museo de la Colegiata de San Isidoro de León.
La pieza está formada por la unión de dos copas de ágata unidas por las bases con un armazón de oro y plata sobredorada junto a perlas, esmeraldas, amatistas y zafiros. Está adornada por las joyas personales de la infanta Urraca de Zamora. La copa superior es la que se identificaría con el cáliz, que es una sencilla pieza al parecer de época romana contemporánea al tiempo de Jesucristo.
Santo Grial de de la Catedral de Valencia
Inicialmente, en el siglo I, San Pedro habría llevado el Santo Grial desde Jerusalén a Roma, en donde fue conservada hasta el siglo III y se utilizó para oficiar misa por los sucesivos papas. En el año 256, ante la persecución del emperador romano Valeriano y con el fin de preservarlo, el papa Sixto II lo entregó en custodia a su diácono San Lorenzo, encargado de administrar los bienes de la Iglesia. San Lorenzo era originario de Huesca y para poner a salvo el cáliz lo hizo llevar a Hispania, a donde llegó en el año 258 hasta sus familiares de las tierras natales oscenses. El cáliz estuvo guardado algún tiempo en la casa familiar de San Lorenzo y pronto fue trasladado a la iglesia de San Pedro el Viejo de Huesca, en donde permaneció bajo la vigilancia del obispo de la diócesis.
A partir del año 711, con la invasión musulmana, el Santo Grial se escondió por diversos lugares del pirineo aragonés. Primero estuvo en la casi inaccesible Cueva de Yebra. Entre los siglos IX y X estuvo protegido en el Monasterio de San Pedro de Siresa. Entre los siglos X y XI se conservó en la Iglesia de Santa María, cuyos restos se encuentran bajo la Ermita de San Adrián de Sásabe de Borau. Entre los años 1014 y 1045 permaneció en la Iglesia de la Corte de Bailo. Luego su presencia se señala por un breve tiempo en la Catedral de Jaca. Desde allí llegó en el año 1071 hasta el monasterio de San Juan de la Peña en donde continuó hasta el año 1399.
Entonces, el rey Martín I de Aragón solicitó la reliquia al abad del monasterio y la mantuvo en su Palacio Real de la Aljafería de Zaragoza. Después fue trasladado a la residencia del rey Martín I de Aragón en Barcelona. Al morir le sucedió, en virtud del Compromiso de Caspe, su sobrino Fernando de Antequera. El hijo de éste y sucesor, el rey Alfonso V de Aragón, en el año 1424 se llevó la pieza a su Palacio Real de Valencia, hoy día desaparecido. En el año 1437 entregó el Santo Grial a la Catedral de Valencia, dejado como garantía por el dinero prestado por la Catedral y el Consejo de la Ciudad para costear la guerra de Nápoles.
Pero ni éste ni los siguientes reyes ya pudieron recuperarlo. Quedó custodiado y venerado en la Catedral de Valencia a partir de entonces. En el año 1809, ante la inminente llegada de las tropas francesas de Napoleón a Valencia, el Santo Grial inició un peregrinaje por Alicante, Mallorca e Ibiza, regresando en el año 1812 de nuevo a la Catedral de Valencia. Durante la Guerra Civil estuvo escondido en el municipio valenciano de Carlet. En la actualidad se expone en la Capilla del Santo Cáliz, en la antigua Sala Capitular de la Catedral de Valencia.
La pieza está formada por la unión de dos copas. La de arriba es de calcedonia finamente pulida y correspondería con el Santo Grial. Parece que podría proceder de un taller grecorromano y estaría fechado entre los siglos II y I a.C. Está acompañada por un añadido posterior de arte islámico, formado por unas asas y un pie de oro que encierra una copa ovalada invertida de calcedonia con un engaste en la base de perlas, rubíes y esmeraldas.
Conclusión
Existen otros lugares tanto en España, por ejemplo el Monasterio de Santa María do Cebreiro de Lugo, así como fuera, por ejemplo la Catedral de San Lorenzo de Génova, en donde también aseguran tener el verdadero Santo Grial. Lo indudable es que esta reliquia es un objeto de peregrinación con un incalculable valor para los que afirman poseerla. Sin embargo, es muy difícil que alguna vez se compruebe con total certeza que el cáliz original sea cualquiera de ellos, o que sea encontrado en el futuro. Ni siquiera se puede saber si realmente existió.
Santo Grial de la Colegiata de León
Santo Grial de la Catedral de Valencia
https://iberhistoria.es/edad-media/cristianos/entradas/el-santo-grial/ |
|
|
|
|
|
 Primeira
Anterior
146 a 160 de 205
Seguinte
Última
|
