Gravity of Mars

Earth vs Mars vs Moon gravity at elevation

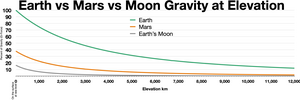
The gravity of Mars is a natural phenomenon, due to the law of gravity, or gravitation, by which all things with mass around the planet Mars are brought towards it. It is weaker than Earth's gravity due to the planet's smaller mass. The average gravitational acceleration on Mars is 3.72076 m/s² (about 38% of the gravity of Earth) and it varies.^[1]

In general, topography-controlled isostasy drives the short wavelength free-air gravity anomalies.^[2] At the same time, convective flow and finite strength of the mantle lead to long-wavelength planetary-scale free-air gravity anomalies over the entire planet.^[3]^[4] Variation in crustal thickness, magmatic and volcanic activities, impact-induced Moho-uplift, seasonal variation of polar ice caps, atmospheric mass variation and variation of porosity of the crust could also correlate to the lateral variations.^[5]^[6]^[7]^[8]^[9]

Over the years models consisting of an increasing but limited number of spherical harmonics have been produced. Maps produced have included free-air gravity anomaly, Bouguer gravity anomaly, and crustal thickness. In some areas of Mars there is a correlation between gravity anomalies and topography. Given the known topography, higher resolution gravity field can be inferred. Tidal deformation of Mars by the Sun or Phobos can be measured by its gravity. This reveals how stiff the interior is, and shows that the core is partially liquid. The study of surface gravity of Mars can therefore yield information about different features and provide beneficial information for future Mars landings.

Measurement

Rotating spherical harmonic, with

{displaystyle ell =0{ ext{ to }}4}

for the vertical, and

{displaystyle m=0{ ext{ to }}4}

for the horizontal. For the Martian C₂₀ and C₃₀, they vary with time because of the seasonal variation of mass of the polar ice caps through the annual sublimation-condensation cycle of carbon dioxide.

To understand the gravity of Mars, its gravitational field strength g and gravitational potential U are often measured. Simply, if Mars is assumed to be a static perfectly spherical body of radius R_M, provided that there is only one satellite revolving around Mars in a circular orbit and such gravitation interaction is the only force acting in the system, the equation would be

{displaystyle {frac {GMm}{r^{2}}}=mromega ^{2},}

where G is the universal constant of gravitation (commonly taken as G = 6.674 × 10⁻¹¹ m³ kg⁻¹ s⁻²),^[10] M is the mass of Mars (most updated value: 6.41693 × 10²³ kg),^[11] m is the mass of the satellite, r is the distance between Mars and the satellite, and ${displaystyle omega }$ is the angular velocity of the satellite, which is also equivalent to ${displaystyle {frac {2pi }{T}}}$ (T is the orbiting period of the satellite).

Therefore, ${displaystyle g={frac {GM}{R_{M}^{2}}}={frac {r^{3}omega ^{2}}{R_{M}^{2}}}={frac {4r^{3}pi ^{2}}{T^{2}R_{M}^{2}}}}$ , where R_M is the radius of Mars. With proper measurement, r, T, and R_M are obtainable parameters from Earth.

However, as Mars is a generic, non-spherical planetary body and influenced by complex geological processes, more accurately, the gravitational potential is described with spherical harmonic functions, following convention in geodesy; see Geopotential model.

{displaystyle U(r,lambda ,psi )=-{frac {GM}{r}}left(1+sum _{ell =2}^{ell =L}left({frac {R}{r}} ight)^{ell }left(C_{ell 0}P_{ell }^{0}(sin psi )+sum _{m=1}^{+ell }(C_{ell m}cos mlambda +S_{ell m}sin mlambda )P_{ell }^{m}(sin psi ) ight) ight),}

^[12]

where ${displaystyle r,psi ,lambda }$ are spherical coordinates of the test point.^[12] ${displaystyle lambda }$ is longitude and ${displaystyle psi }$ is latitude. ${displaystyle C_{ell m}}$ and ${displaystyle S_{ell m}}$ are dimensionless harmonic coefficients of degree ${displaystyle l}$ and order ${displaystyle m}$ .^[12] ${displaystyle P_{ell }^{m}}$ is the Legendre polynomial of degree ${displaystyle l}$ with ${displaystyle m=0}$ and is the associated Legendre polynomial with ${displaystyle m>0}$ . These are used to describe solutions of Laplace's equation.^[12] ${displaystyle R}$ is the mean radius of the planet.^[12] The coefficient ${displaystyle C_{ell 0}}$ is sometimes written as ${displaystyle J_{n}}$ .

The lower the degree ${displaystyle ell }$ and order ${displaystyle m}$ , the longer wavelength of anomaly it represents. In turn, long-wavelength gravity anomaly is influenced by global geophysical structures.
The higher the degree ${displaystyle ell }$ and order ${displaystyle m}$ , the shorter wavelength of anomaly it represents. For degree over 50, it has been shown that those variations have high correlation with the topography.^[13] Geophysical interpretation of surface features could further help deriving a more complete picture of the Martian gravity field, though misleading results could be produced.^[13]

The oldest technique in determining the gravity of Mars is through Earth-based observation. Later with the arrival of uncrewed spacecraft, subsequent gravity models were developed from radio tracking data.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

Gold and silver NFT blockchain technology icon isolated on black background. Non fungible token. Digital crypto art concept. Long shadow style. Vector.

In ‘Back to the Future’ (1985) you can see a portrait of Thomas Edison in Doc’s house when Marty travels back to 1955. This was a good prop to illustrate the time period, as no modern scientist like Doc would ever respect a degenerate conman like Edison.

In Back to the Future, Doc displays pictures of Newton, Franklin, Edison, and Einstein in his 1955 home while discussing time travel with Marty. All men whose work influenced Doc's invention.

Definitive proof of Einstein's theory of relativity... 'Epoch making'...

Currently Unavailable. Contact us if you would like to be placed on a want list or to be notified if a similar item is available.

Gravity of Mars

Measurement