|
|
| BARILOCHENSE6999 ha eliminado este mensaje |
|
|
|
|



16. Génesis 49:27 Benjamín es lobo arrebatador; A la mañana comerá la presa, Y a la tarde repartirá los despojos.
169. Romanos 11:1 Digo, pues: ¿Ha desechado Dios a su pueblo? En ninguna manera. Porque también yo soy israelita, de la descendencia de Abraham, de la tribu de Benjamín. 170. Filipenses 3:5 circuncidado al octavo día, del linaje de Israel, de la tribu de Benjamín, hebreo de hebreos; en cuanto a la ley, fariseo;
PABLO, ESTA EN FUNCION A LA MISMA SANTA CENA, OSEA EL MISMO RELOJ.
JERUSALEN ESTABA EN LA TRIBU DE BENJAMIN, OSEA QUE ES OBVIO QUE LA NUEVA JERUSALEN ES PABLO MISMO
PABLO/PEQUEÑO/PERRO/LOBO/GUERRA/MARTE/GRIAL
PABLO ES UN TIPO DEL GRIAL MISMO
16. Génesis 49:27 Benjamín es lobo arrebatador; A la mañana comerá la presa, Y a la tarde repartirá los despojos.
169. Romanos 11:1 Digo, pues: ¿Ha desechado Dios a su pueblo? En ninguna manera. Porque también yo soy israelita, de la descendencia de Abraham, de la tribu de Benjamín. 170. Filipenses 3:5 circuncidado al octavo día, del linaje de Israel, de la tribu de Benjamín, hebreo de hebreos; en cuanto a la ley, fariseo;
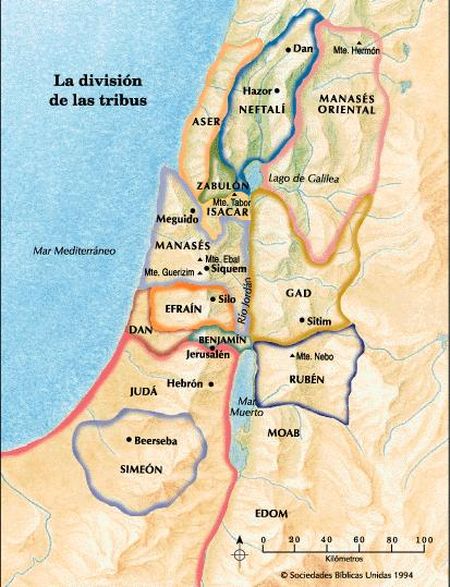 LAS DOCE TRIBUS DE ISRAEL LAS DOCE TRIBUS DE ISRAEL

13 HIJOS MAS DINA, LA UNICA HIJA MUJER
JABOB=ISRAEL=VENCEDOR

The classic logarithmic Golden Spiral

LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
| milky way in Simple Gematria Equals: 119 |
( |
m 13 |
i9 |
l 12 |
k 11 |
y 25 |
0 |
w 23 |
a1 |
y 25 |
) |
| queen mary in Simple Gematria Equals: 119 |
( |
q 17 |
u 21 |
e5 |
e5 |
n 14 |
0 |
m 13 |
a1 |
r 18 |
y 25 |
|
| hebrew calendar in Simple Gematria Equals: 119 |
( |
h8 |
e5 |
b2 |
r 18 |
e5 |
w 23 |
0 |
c3 |
a1 |
l 12 |
e5 |
n 14 |
d4 |
a1 |
r 18 |
| mary magdalene in Simple Gematria Equals: 119 |
( |
m 13 |
a1 |
r 18 |
y 25 |
0 |
m 13 |
a1 |
g7 |
d4 |
a1 |
l 12 |
e5 |
n 14 |
e5 |
|

| milky way in Simple Gematria Equals: 119 |
( |
m 13 |
i9 |
l 12 |
k 11 |
y 25 |
0 |
w 23 |
a1 |
y 25 |
) |
| queen mary in Simple Gematria Equals: 119 |
( |
q 17 |
u 21 |
e5 |
e5 |
n 14 |
0 |
m 13 |
a1 |
r 18 |
y 25 |
|
| hebrew calendar in Simple Gematria Equals: 119 |
( |
h8 |
e5 |
b2 |
r 18 |
e5 |
w 23 |
0 |
c3 |
a1 |
l 12 |
e5 |
n 14 |
d4 |
a1 |
r 18 |
| mary magdalene in Simple Gematria Equals: 119 |
( |
m 13 |
a1 |
r 18 |
y 25 |
0 |
m 13 |
a1 |
g7 |
d4 |
a1 |
l 12 |
e5 |
n 14 |
e5 |
|
|
|
|
|
|
Sabemos que Vesica Piscis esta en funcion al a los 153 peces de Juan 21:11.
 Aqui tenemos a Pi - la circunferencia del toro y la vesica piscis 256/153 equivalente a la raiz cuadrada de 3 En el hipercubo las coordinadas binarias de Piscis son decimal 3 y binario 11 153 los pescados de Jesus en la biblia
Sapientia Aedificavit Sibi Domum. Es decir, "la sabiduría ha edificado aquí su casa". Resulta curioso que la misma frase aparece en el Evangelio de María Magdalena, un texto apócrifo. Se dice que en el interior de esta iglesia y de otras muchas de Venecia está escondido el tesoro de los templarios. Pero no hay ninguna prueba de ello. Para terminar ya con esta entrada me gustaría que nos acercásemos un momento a uno de los edificios más emblemáticos de Venecia: el Palacio Ducal.
|
|
|
|
|

  
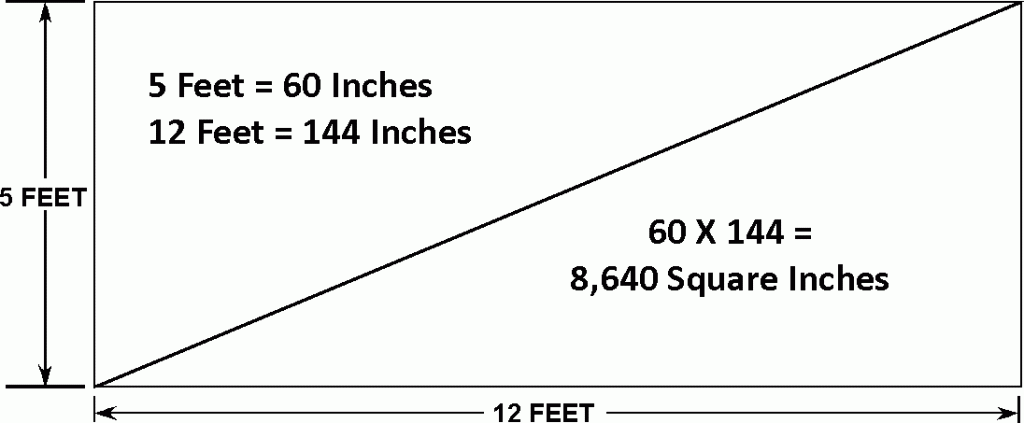
  Las piedras de estaciones de Stonehenge forman un rectángulo con la proporción de 5:12 - Mapa con Stonehenge y la isla Caldey mostrando la distancia proporcional de 12,369 - eso es el número de lunas llenas por año Las piedras de estaciones de Stonehenge forman un rectángulo con la proporción de 5:12 - Mapa con Stonehenge y la isla Caldey mostrando la distancia proporcional de 12,369 - eso es el número de lunas llenas por año
5. Stonehenge - geometría secreta - triángulo de 5:12, estrella de 7 puntos, número 1234, Stonehenge+isla Lundy -- Nueva York con un triángulo en el Parque Central como Stonehenge tiene -- Stonehenge: la proporción original de 5:12 -- Stonehenge: William Stukeley y druidas para la francmasonería -- Stonehenge: una estrella de 7 puntos e Isis -- Distancias: Stonehenge - Averbury - la colina de Silbury -- Stonehenge, monumento de Averbury y el monumento de Silbury - números con sol, luna y el cubo de Isis -- Stonehenge y su cantera en las montañas Preseli en Gales apr. 130 millas en el oeste -- El número 1234: Stonehenge - isla Lundy 123,4 millas -- Triángulo Stonehenge - cantera de Preseli - isla Lundy: 5:12 -- Copias de Stonehenge en el mundo - francmasones e iluminados criminales ponen sus símbolos de poder - p.e. en Lima en el Perú -- Hay una copia de Stonehenge en el centro de Lima en el parque de fontanas (parque de la reserva) -- 6. Milla y pies y luna y Tierra - números 3456, 108, 528 -- La milla y Stonehenge: 108 millas reales = 123,4 millas internacionales -- Número 108: Tierra, religiones, luna etc. -- Luna y número 108: radio 1080 millas reales -- Pie y Tierra: 360 grados x 365,242 días x pie x 1.000 = circunferencia de la Tierra -- Milla y Tierra: 12 elevado 5 dividido por 10 millas = circunferencia de la Tierra -- El pie inglés es el origen del sistema antiguo de mediciones -- 7. Stonehenge, la cantera y las islas 5:12 - Newton y su número 33 -- Stonehenge: isla Lundy + isla Caldey: 3:2 - Stonehenge-isla Caldey=12,369 = número de lunas llenas por año -- Newton: su escala de temperatura y el número 33
 Aqui tenemos a Pi - la circunferencia del toro y la vesica piscis 256/153 equivalente a la raiz cuadrada de 3 En el hipercubo las coordinadas binarias de Piscis son decimal 3 y binario 11 153 los pescados de Jesus en la biblia
|
|
|
|
|
Madrid celebra a Leonardo da Vinci y expone sus Códices y la Tavola Lucana
EFE - Madrid

Madrid celebra a Leonardo da Vinci y expone sus Códices y la Tavola Lucana
Con el objetivo de mostrar no solo al genio sino al "hombre de carne y hueso" que fue Leonardo da Vinci, la Biblioteca Nacional y el Palacio de las Alhajas conmemoran desde hoy el quinto centenario de su muerte con una exposición que ofrece dos "joyas": los Códices de Madrid y la Tavola Lucana.
"Leonardo da Vinci: los rostros del genio" es el título de la exposición que ha sido presentada hoy por su comisario, Christian Gálvez, presentador de televisión y experto en la figura del maestro renacentista, y la directora de la Biblioteca Nacional (BNE), Ana Santos, quienes han destacado la oportunidad de ver tanto los Códices, los dos únicos textos de Leonardo que se conservan en España, como la Tavola Lucana, identificada como el autorretrato del italiano.
Una exposición con dos sedes, el Palacio de las Alhajas y la BNE, con las que Madrid se une a los actos de conmemoración del quinto centenario de la muerte de Da Vinci, que se cumple el 2 de mayo de 2019.
Un gran cubo con los posibles rostros de Leonardo reciben al visitante en el Palacio de las Alhajas, una forma de reflejar "la mente poliédrica de Da Vinci y la transversalidad de su conocimiento", ha explicado hoy Gálvez en la presentación de esta exposición, que enseña cómo para él era tan importante la obra acabada como la inacabada.
Imágenes de los coetáneos de Da Vinci acompañan a reproducciones de sus principales obras pictóricas, entre las que destacan "La última cena" y " La Gioconda" y sus trabajos preparatorios, junto a sus estudios de anatomía que abordó tanto con un propósito artístico como científico.
Además, la exposición ofrece numerosas maquetas tanto físicas como virtuales de las avanzadas máquinas e ingenios ideadas por un hombre "que nunca dejó de volar con la imaginación", ha indicado Gálvez.
Tras un apartado dedicado a las posibles "caras" de Leonardo, la muestra expone por primera vez en España la "Tavola Lucana", descubierta en 2008 por el historiador de arte Nicola Barbatelli, quien ha asegurado hoy que es el único retrato que reúne todas las condiciones para asegurar que representa al maestro florentino.
Estudios de pigmentación, materiales, técnicas y detalles en el cuadro han determinado que se trataba de un autorretrato de Da Vinci, ha indicado Barbatelli.
Al mismo tiempo, la Biblioteca Nacional abre hoy por primera vez su vestíbulo como espacio expositivo para mostrar dos "joyas" de sus fondos, los Códices Madrid I y Madrid II de Leonardo da Vinci.
Redactados en torno a 1500 con su escritura inversa (era zurdo), los códices son los únicos que conserva España de la colección de manuscritos que llegó a Madrid a principios del XVII: El Códice I es un tratado de mecánica y estática mientras que el II es un estudio de fortificación, estática y geometría.
Aunque la exposición permanecerá abierta hasta el 19 de mayo de 2019, los códices originales solo podrán ser contemplados un mes, en el que se irán alternando, para garantizar su adecuada conservación, ha indicado la directora de la BNE, que ha explicado que luego serán sustituidos por sus facsímiles.
Acompañarán a estos dos volúmenes otras 32 obras de la colección de la BNE que contextualizan las vida y obras de Leonardo da Vinci, así como reconstrucciones de máquinas dibujadas en los códices por el maestro y de uno de los mayores proyectos que acometió, el enorme caballo diseñado para Ludovico Sforza.
https://www.eldiario.es/cultura/Madrid-Leonardo-Codices-Tavola-Lucana_0_840616533.html |
|
|
|
|
|

LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
Incendio Notre Dame: Última hora de la catedral de París (15 DE ABRIL)

 Incendio Notre Dame (París), en directo (Bertrand Guay / AFP)
PHI A NOTRE-DAME
A la catredal de Notre Dame hi observem més rectanlges auris: Creat per Mario Pastor 
The DaVinci Code, Notre Dame Cathedral from DaVinci Code
original movie prop
 
        

August 23, 2018/

The Golden Section (aka Golden Mean, and Golden Ratio) phys.org
We use math in architecture on a daily basis to solve problems. We use it to achieve both functional and aesthetic advantages. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance. As you will see from some of the examples below, the application of mathematical principles can result in beautiful and long-lasting architecture which has passed the test of time.
Using Math in Architecture for Function and Form
We use math in architecture every day at our office. For example, we use math to calculate the area of a building site or office space. Math helps us to determine the volume of gravel or soil that is needed to fill a hole. We rely on math when designing safe building structures and bridges by calculating loads and spans. Math also helps us to determine the best material to use for a structure, such as wood, concrete, or steel.
“Without mathematics there is no art.” – Luca Pacioli, De divina proportione, 1509
Architects also use math when making aesthetic decisions. For instance, we use numbers to achieve attractive proportion and harmony. This may seem counter-intuitive, but architects routinely apply a combination of math, science, and art to create attractive and functional structures. One example of this is when we use math to achieve harmony and proportion by applying a well-known principle called the Golden Section
Math and Proportion – The Golden Section

Perfect proportions of the human body – The Vitruvian Man – by Leonardo da Vinci.
We tend to think of beauty as purely subjective, but that is not necessarily the case. There is a relationship between math and beauty. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance.
The Golden Section is one example of a mathematical principle that is believed to result in pleasing proportions. It was mentioned in the works of the Greek mathematician Euclid, the father of geometry. Since the 4th century, artists and architects have applied the Golden Section to their work.
The Golden Section is a rectangular form that, when cut in half or doubled, results in the same proportion as the original form. The proportions are 1: the square root of 2 (1.414) It is one of many mathematical principles that architects use to bring beautiful proportion to their designs.
Examples of the Golden Section are found extensively in nature, including the human body. The influential author Vitruvius asserted that the best designs are based on the perfect proportions of the human body.
Over the years many well-known artists and architects, such as Leonardo da Vinci and Michelangelo, used the Golden Section to define the dimensions and proportions in their works. For example, you can see the Golden Section demonstrated in DaVinci’s painting Mona Lisa and his drawing Vitruvian Man.
Famous Buildings Influenced by Mathematical Principles
Here are some examples of famous buildings universally recognized for their beauty. We believe their architects used math and the principals of the Golden Section in their design:
Parthenon
The classical Doric columned Parthenon was built on the Acropolis between 447 and 432 BC. It was designed by the architects Iktinos and Kallikrates. The temple had two rooms to shelter a gold and ivory statue of the goddess Athena and her treasure. Visitors to the Parthenon viewed the statue and temple from the outside. The refined exterior is recognized for its proportional harmony which has influenced generations of designers. The pediment and frieze were decorated with sculpted scenes of Athena, the Gods, and heroes.

Parthenon Golden Section
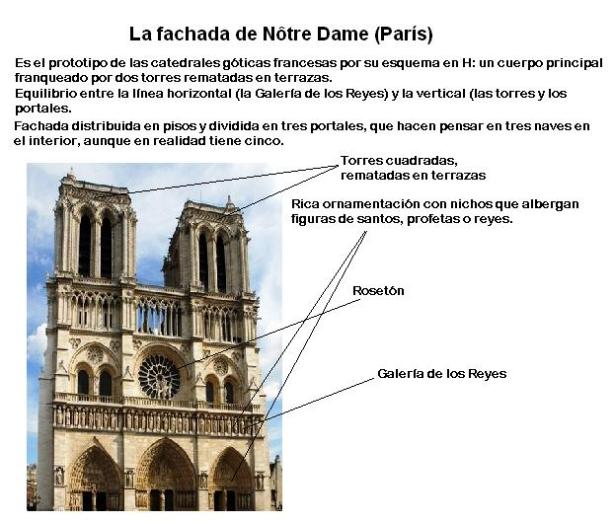
Notre Dame Cathedral in Paris
Built on the Ile de la Cite, Notre Dame was built on the site of two earlier churches. The foundation stone was laid by Pope Alexander III in 1163. The stone building demonstrates various styles of architecture, due to the fact that construction occurred for over 300 years. It is predominantly French Gothic, but also has elements of Renaissance and Naturalism. The cathedral interior is 427 feet x 157 feet in plan. The two Gothic towers on the west façade are 223 feet high. They were intended to be crowned by spires, but the spires were never built. The cathedral is especially loved for its three stained glass rose windows and daring flying buttresses. During the Revolution, the building was extensively damaged and was saved from demolition by the emperor Napoleon.

Notre Dame Cathedral in Paris
Taj Mahal
Built in Agra between 1631 and 1648, the Taj Mahal is a white marble mausoleum designed by Ustad-Ahmad Lahori. This jewel of Indian architecture was built by Emperor Shah Jahan in memory of his favorite wife. Additional buildings and elements were completed in 1653. The square tomb is raised and is dramatically located at the end of a formal garden. On the interior, the tomb chamber is octagonal and is surrounded by hallways and four corner rooms. Building materials are brick and lime veneered with marble and sandstone.

Taj Mahal designed by Ustad-Ahmad Lahori
As you can see from the above examples, the application of mathematical principles can result in some pretty amazing architecture. The architects’ work reflects eye-catching harmony and balance. Although these buildings are all quite old, their designs have pleasing proportions which have truly passed the test of time.
https://bleckarchitects.com/math-in-architecture/
|
|
|
|
|
|
|







 




|

LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
Incendio Notre Dame: Última hora de la catedral de París (15 DE ABRIL)

 Incendio Notre Dame (París), en directo (Bertrand Guay / AFP)
PHI A NOTRE-DAME
A la catredal de Notre Dame hi observem més rectanlges auris: Creat per Mario Pastor 
The DaVinci Code, Notre Dame Cathedral from DaVinci Code
original movie prop
HEXAGONO=OCTAHEDRO =ESTRELLA DE 6 PUNTAS= SATURNO =CUBO/HEXAGONO= ESPACIO/TIEMPO =1 DE REYES 6:20 Y APOCALIPSIS 21:16
EL SEXTO DIA ES EL VIERNES Y EL OCTAVO EL DOMINGO. INCREIBLE
   

August 23, 2018/

The Golden Section (aka Golden Mean, and Golden Ratio) phys.org
We use math in architecture on a daily basis to solve problems. We use it to achieve both functional and aesthetic advantages. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance. As you will see from some of the examples below, the application of mathematical principles can result in beautiful and long-lasting architecture which has passed the test of time.
Using Math in Architecture for Function and Form
We use math in architecture every day at our office. For example, we use math to calculate the area of a building site or office space. Math helps us to determine the volume of gravel or soil that is needed to fill a hole. We rely on math when designing safe building structures and bridges by calculating loads and spans. Math also helps us to determine the best material to use for a structure, such as wood, concrete, or steel.
“Without mathematics there is no art.” – Luca Pacioli, De divina proportione, 1509
Architects also use math when making aesthetic decisions. For instance, we use numbers to achieve attractive proportion and harmony. This may seem counter-intuitive, but architects routinely apply a combination of math, science, and art to create attractive and functional structures. One example of this is when we use math to achieve harmony and proportion by applying a well-known principle called the Golden Section
Math and Proportion – The Golden Section

Perfect proportions of the human body – The Vitruvian Man – by Leonardo da Vinci.
We tend to think of beauty as purely subjective, but that is not necessarily the case. There is a relationship between math and beauty. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance.
The Golden Section is one example of a mathematical principle that is believed to result in pleasing proportions. It was mentioned in the works of the Greek mathematician Euclid, the father of geometry. Since the 4th century, artists and architects have applied the Golden Section to their work.
The Golden Section is a rectangular form that, when cut in half or doubled, results in the same proportion as the original form. The proportions are 1: the square root of 2 (1.414) It is one of many mathematical principles that architects use to bring beautiful proportion to their designs.
Examples of the Golden Section are found extensively in nature, including the human body. The influential author Vitruvius asserted that the best designs are based on the perfect proportions of the human body.
Over the years many well-known artists and architects, such as Leonardo da Vinci and Michelangelo, used the Golden Section to define the dimensions and proportions in their works. For example, you can see the Golden Section demonstrated in DaVinci’s painting Mona Lisa and his drawing Vitruvian Man.
Famous Buildings Influenced by Mathematical Principles
Here are some examples of famous buildings universally recognized for their beauty. We believe their architects used math and the principals of the Golden Section in their design:
Parthenon
The classical Doric columned Parthenon was built on the Acropolis between 447 and 432 BC. It was designed by the architects Iktinos and Kallikrates. The temple had two rooms to shelter a gold and ivory statue of the goddess Athena and her treasure. Visitors to the Parthenon viewed the statue and temple from the outside. The refined exterior is recognized for its proportional harmony which has influenced generations of designers. The pediment and frieze were decorated with sculpted scenes of Athena, the Gods, and heroes.

Parthenon Golden Section
Notre Dame Cathedral in Paris
Built on the Ile de la Cite, Notre Dame was built on the site of two earlier churches. The foundation stone was laid by Pope Alexander III in 1163. The stone building demonstrates various styles of architecture, due to the fact that construction occurred for over 300 years. It is predominantly French Gothic, but also has elements of Renaissance and Naturalism. The cathedral interior is 427 feet x 157 feet in plan. The two Gothic towers on the west façade are 223 feet high. They were intended to be crowned by spires, but the spires were never built. The cathedral is especially loved for its three stained glass rose windows and daring flying buttresses. During the Revolution, the building was extensively damaged and was saved from demolition by the emperor Napoleon.

Notre Dame Cathedral in Paris
Taj Mahal
Built in Agra between 1631 and 1648, the Taj Mahal is a white marble mausoleum designed by Ustad-Ahmad Lahori. This jewel of Indian architecture was built by Emperor Shah Jahan in memory of his favorite wife. Additional buildings and elements were completed in 1653. The square tomb is raised and is dramatically located at the end of a formal garden. On the interior, the tomb chamber is octagonal and is surrounded by hallways and four corner rooms. Building materials are brick and lime veneered with marble and sandstone.

Taj Mahal designed by Ustad-Ahmad Lahori
As you can see from the above examples, the application of mathematical principles can result in some pretty amazing architecture. The architects’ work reflects eye-catching harmony and balance. Although these buildings are all quite old, their designs have pleasing proportions which have truly passed the test of time.
https://bleckarchitects.com/math-in-architecture/
|
|
|
|
|
|
|
.

|
|
|
|
|
.

|
|
|
|
|
Entre 18 mil postulantes, la NASA eligió 12 nuevos astronautas: 7 hombres y 5 mujeres
07/06/2017-20:21Vida
El proceso de elección tuvo el mayor número de solicitantes de la historia.

Selfie. Los 12 nuevos astronautas seleccionados por la NASA. AFP
La NASA seleccionó a siete hombres y cinco mujeres como sus nuevos astronautas, en un proceso de selección que tuvo el mayor número de solicitantes de su historia.

Los 12 nuevos astronautas seleccionados por la NASA. (Michael Ciaglo/Houston Chronicle via AP)
El anuncio de la promoción de astronautas del 2017 se hizo en el Centro Espacial Johnson, en Houston, que contó con la presencia del vicepresidente de los Estados Unidos, Mike Pence.
“
Ustedes son lo mejor de nosotros. Con el presidente Donald Trump, Estados Unidos liderará en el espacio una vez más y el mundo se maravillará.
Mike Pence, vicepresidente de los Estados Unidos
http://eju.tv/2017/06/entre-18-mil-postulantes-la-nasa-eligio-12-nuevos-astronautas-7-hombres-y-5-mujeres/
|
|
|
 Primer Primer
 Anterior
74 a 88 de 163
Siguiente Anterior
74 a 88 de 163
Siguiente Último
Último
|

