|
|
EL HIPERCUBO, LA CUARTA DIMENSION, EL TIEMPO, LA LEY DE LA RELATIVIDAD DE EINSTEIN Y SU NEXO CON MARCOS 15:33
33. Marcos 15:33: Cuando vino la hora SEXTa, hubo tinieblas sobre toda la tierra hasta la hora novena. (CLAVE MERCURIO-ORION-ISHTAR GATE)

Decimal --- Binario --- Cuaternario
00 -------- 0000 ------ 00
01 -------- 0001 ------ 01
02 -------- 0010 ------ 02
03 -------- 0011 ------ 03
04 -------- 0100 ------ 10
05 -------- 0101 ------ 11
06 -------- 0110 ------ 12
07 -------- 0111 ------ 13
08 -------- 1000 ------ 20
09 -------- 1001 ------ 21
10 -------- 1010 ------ 22
11 -------- 1011 ------ 23
12 -------- 1100 ------ 30
13 -------- 1101 ------ 31
14 -------- 1110 ------ 32
15 -------- 1111 ------ 33
Las Triadas "que nos elevan" como acordes (11, 111, 1111) a través de sus ejes o colúmnas pitagóricas. Los puntos de corte de dos dimensiones.
Aquí el el 3, 7 y 15 decimal, o 3, 13, 33 cuaternario. Puntos, entiendo, de la singularidad en tres planos diferentes. O como fusión de contrarios.
3 veces 3 que nos llevan hasta la eclosión del huevo -singularidad fecundativa-.

3 veces 3 como el PLATO (PI-LATO) de Giza. 3 pirámides grandes, 3 pirámides pequeñas (6) y 9 (3+3+3) en total. 369.
http://www.burbuja.info/inmobiliaria/conspiraciones/297306-hilo-oficial-indigomerovingio-148.html
 |
Click para ampliar |
  Lo que me lleva a relacionar esto del 3 veces 3 con los armónicos solfeggio y sus puntos de corte o frecuencias doradas, donde el "dragón se eleva" Lo que me lleva a relacionar esto del 3 veces 3 con los armónicos solfeggio y sus puntos de corte o frecuencias doradas, donde el "dragón se eleva"
 |
Click para ampliar |
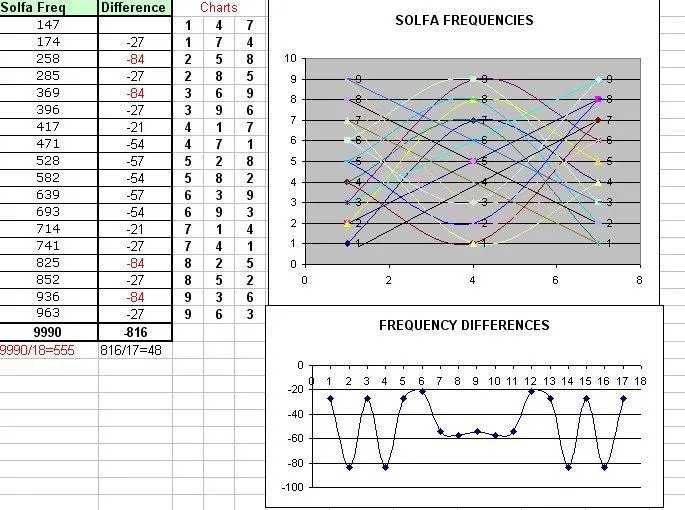 Bettle-Juice, Beetle-Juice, Beetle-Juice.Veo ademas que la suma reducida es 3-6-9. Bettle-Juice, Beetle-Juice, Beetle-Juice.Veo ademas que la suma reducida es 3-6-9.
 |
Click para ampliar |
 3 veces 3. 3 veces 3.
Viene de digitalización de primera semana de curso:
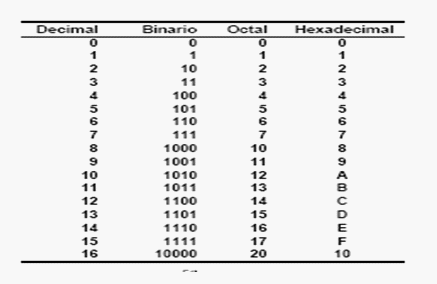
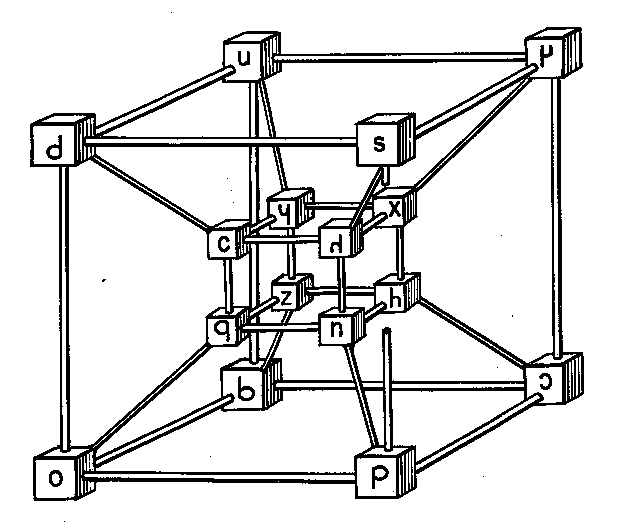
El concepto, que no es nuevo, es que los dieciséis primeros números decimales se pueden mostrar en un nibble binario (medio Byte) resultando 1111 como indicaba IM al representar las coordenadas de los vértices del cubo 4D...
Ahora viene el nuevo apunte...
Que pasa si mostramos esos mismo número decimales en un sistema en base cuatro o cuaternario:
Decimal --- Binario --- Cuaternario
00 -------- 0000 ------ 00
01 -------- 0001 ------ 01
02 -------- 0010 ------ 02
03 -------- 0011 ------ 03
04 -------- 0100 ------ 10
05 -------- 0101 ------ 11
06 -------- 0110 ------ 12
07 -------- 0111 ------ 13
08 -------- 1000 ------ 20
09 -------- 1001 ------ 21
10 -------- 1010 ------ 22
11 -------- 1011 ------ 23
12 -------- 1100 ------ 30
13 -------- 1101 ------ 31
14 -------- 1110 ------ 32
15 -------- 1111 ------ 33
Inquietante... 
¿Esta letra en base cuatro como se podría representar físicamente? Considero que lo mas adecuado sería un tetraedro regular (formado por 4 triángulos equiláteros), el primero de los sólidos platónicos. Donde cada uno de sus cuatro vértices se encuentran a distancias simétricas entre ellas.
Como para representar el 15 decimal (el 33 en base 4) se necesitan dos dígitos en cuaternario, la forma física de integrar ambas letras sería mediante dos tetraedros unidos en que su vórtices continuaran de forma simétrica.
Resumiendo se puede decir, que un hipercubo es lo mismo que lo que se suele representar como Merkaba
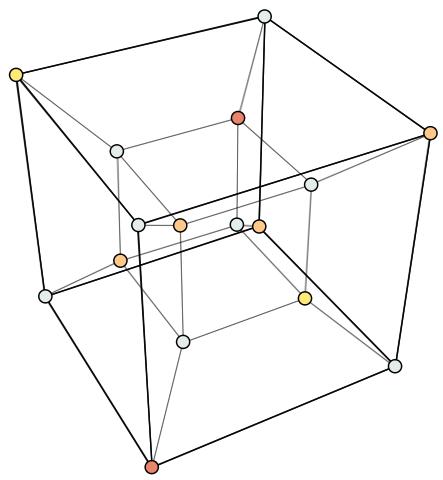


...
..
.
Y que este simbolismo:

Es igual a este:

O al menos que debe representar un concepto muy similar...
|
|
|
|
|
Enki
De Wikipedia, la enciclopedia libre
Enki o Enkil (en sumerio: dEN.KI) es un dios en la mitología sumeria, más tarde conocido como Ea en las mitologías acadia y babilónica. Significa El señor de la tierra, es hermano del dios Enlil, e hijo de An. Su misión será la de crear a los hombres e impulsar a que otras divinidades los creen. Dota a los humanos con las artes, oficios y medios técnicos para la agricultura.
Descripción[editar]
Enki (de En= Señor, ki = tierra), o «Ea» (quizás se trata de un nombre compuesto por los signos E = "templo" o "casa" y A = "agua"), como lo denominaron los acadios y babilonios, asociándolo quizás a un antiguo dios acadio de nombre tal vez "Ia".
Se le asocia con el mundo acuático y reina en el Apsu, un lugar situado en las profundidades de la tierra, donde fluyen "las aguas primordiales". Enki Nudimmud (uno de sus epítetos más usados, algo así como "hacedor") es el dios de la sabiduría, señor de la magia la construcción, las artes, el diseño y la creación. Es uno de los tres dioses más importantes (con Enlil y Anu) de la cultura mesopotámica, surgida en el valle del Tigris y el Éufrates.
Es el creador de la humanidad, según lo que se cuenta en la leyenda épica acadia de Atrahasis, únicamente con el propósito de liberar de su trabajo a los dioses, utilizó un homínido ya existente el cual manipuló de alguna manera para hacerlo capaz de entender y satisfacer las necesidades de los dioses. También es asimismo considerado su salvador, ya que alertó sobre el diluvio universal (abubu en acadio y a.ma.ru en sumerio ) a Ziusudra (el nombre babilonio de este mismo personaje sería Utnapishtim). Este diluvio lo promovió Enlil, el "Señor del Cielo (del aire o de la atmósfera)", aparentemente preocupado por la excesiva proliferación del género humano y su ruidoso comportamiento. Enlil consiguió convencer al resto de los dioses, reunidos en asamblea, para que autorizasen el exterminio de la Humanidad. Esta leyenda, probablemente, dio origen al posterior relato bíblico de Noé y el diluvio universal.
También es el autor de un cierto tipo de seres representados portando una especie de traje de pez, llamados apkallu (ab-gal-lu "gran hombre del mar" o "hombre del gran mar" en sumerio) que durante el día enseñaban a los humanos todo tipo de materias y durante la noche se retiraban al fondo del mar.
Su templo principal era el "E-engur", situado en la ciudad de Eridu. Enki era el detentor de los misteriosos "Me", término intraducible que se viene interpretando como "Poderes" o "Leyes divinas", y que los dioses podían portar como adornos o joyas.
El auténtico nombre de Sumeria era, en su lengua, "KI.EN.GI" literalmente "la tierra del señor del cañaveral", quizás en referencia a este dios en particular, del que se especifica en un texto muy difundido que estableció su morada entre cañaverales. El dios Enki siempre gozó de una cierta preeminecia a pesar de no ser el titular del panteón mesopotámico, de hecho su hijo Marduk heredó el trono celeste, en detrimento de la descendencia de Enlil.
Sus símbolos eran la cabra y el pez, que más tarde se refundieron en una única bestia denominada Capricornio. De ahí que, astronómicamente, se asocie a las constelaciones de Acuario y Capricornio, aunque también se le relaciona con el planeta Mercurio. Se representa como una figura masculina portando o vertiendo agua.
Véase también[editar]
http://es.wikipedia.org/wiki/Enki
|
|
|
|
|
|
Tesseract crop circle
Hypercube fourth dimension
The spacetime of our universe is usually interpreted from a Euclidean space perspective, which regards space as consisting of three dimensions, and time as consisting of one dimension, the 'fourth dimension'.
_________________
Everything is Connected and there are no
coincidences
|
|
|
|
|
Cuarta dimensión
De Wikipedia, la enciclopedia libre
Para otros usos de este término, véase Cine 4D.

Hipercubo de 4 dimensiones espaciales girando, tal como se vería proyectado en el espacio tridimensional.
El término cuarta dimensión aparece en diversos contextos como la física, las matemáticas y la ciencia ficción. En cada contexto el significado es diferente:
El interés en las dimensiones más altas alcanzó su clímax entre 1870 y 1920.[1] En esos años se convirtió en tema frecuente en la literatura fantástica, el arte e incluso algunas teorías científicas. La cuarta dimensión, entendida como dimensión espacial adicional (no como dimensión temporal, como en la teoría de la relatividad) apareció en las obras literarias de Oscar Wilde, Fiódor Dostoyevski, Marcel Proust, H. G. Wells y Joseph Conrad, inspiró algunas obras musicales de Alexander Scriabin, Edgar Varèse y George Antheil y algunas obras plásticas de Pablo Picasso y Marcel Duchamp influyendo en el desarrollo del cubismo. Incluso personajes tan diversos como el psicólogo William James, la escritora Gertrude Stein o el socialista revolucionario Vladimir Lenin se interesaron en el tema.
Igualmente los matemáticos habían estado interesados en el tema al tratar de generalizar los conceptos de la geometría euclídea tridimensional. El matemático Charles L. Dodgson, que enseñó en la Universidad de Oxford, deleitó a generaciones de escolares escribiendo libros, bajo el pseudónimo de Lewis Carroll, que incorporaban algunas ideas sobre la cuarta dimensión. Desde el punto de vista académico, el estudio general de la geometría de la cuarta dimensión en gran parte resultado de los trabajos de Bernhard Riemann. Charles Howard Hinton, matemático y escritor de ciencia ficción británico, acuñó muchos neologismos para describir elementos en la cuarta dimensión. De acuerdo con el Oxford English Dictionary, fue el primero en emplear la palabra tesseract en su libro Una nueva era del pensamiento. También inventó las palabras “kata” (del griego “abajo”) y “ana” (del griego “arriba”) para describir las dos direcciones opuestas en la cuarta dimensión, equivalentes a derecha-izquierda, arriba-abajo, y adelante-atrás.
Los trabajos matemáticos sobre geometrías multidimensionales y geometrías no euclídeas habían sido considerado por los físicos como simples abstracciones matemáticas hasta que Henri Poincaré probó que el grupo de transformaciones de Lorentz que dejaban invariantes las ecuaciones del electromagnetismo podían ser interpretadas como "rotaciones" en un espacio de cuatro dimensiones. Más tarde, los trabajos de Einstein y la interpretación geométrica de estos por parte de Hermann Minkowski llevaron a la aceptación de la cuarta dimensión como una descripción necesaria para explicar los hechos observados relacionados con el electromagnetismo. Sin embargo, aquí la "cuarta dimensión" no era un lugar separado del espacio tridimensional (como en varias de las obras de ficción de la época) ni tampoco una dimensión espacial análoga a las otras tres dimensiones espaciales, sino una dimensión temporal que sólo puede recorrerse hacia el futuro. En la teoría general de la relatividad el campo gravitatorio es explicado como un efecto geométrico de la curvatura de un espacio-tiempo de cuatro dimensiones.
Más tarde, la teoría de Kaluza-Klein propuso que no sólo el campo gravitatorio podía ser interpretado de forma más sencilla como curvatura de un "espacio" de más de tres dimensiones, sino que si se introducía una nueva dimensión espacial enrollada o «compactificada», también el campo electromagnético podía ser interpretado como un efecto geométrico de la curvatura de dimensiones superiores. Así, la Kaluza proponía una teoría de campo unificado del electromagnetismo y la gravedad en un espacio-tiempo de cinco dimensiones, con una dimensión temporal, tres dimensiones espaciales extendidas y una dimensión espacial «compactificada» adicional, que, debido a su condición de compactificada, no era directamente visible pero su efecto era perceptible en forma de campo electromagnético.
Cuarta dimensión en matemáticas[editar]
Un ángulo recto se describe como un cuarto de una revolución. La Geometría Cartesiana escoge direcciones ortogonales arbitrariamente a través del espacio, lo que significa que cada dirección está en ángulo recto con las demás. Las 3 dimensiones ortogonales del espacio se conocen como altitud, longitud y latitud. La Cuarta Dimensión por lo tanto es la dirección en el espacio con ángulo recto a las 3 direcciones observables.
Vectores espaciales[editar]
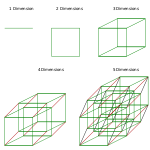
Demostración de 1 a 5 dimensiones.
Un vector espacial es un conjunto de vectores, los cuales podemos imaginarlos como flechas, que proviene de un simple lugar llamado origen (vectores geométricos), que apuntan a otros lugares.
Un punto es un objeto de cero dimensiones. No tiene extensión en el espacio ni propiedades, como una flecha pero sin longitud. Este vector es llamado el vector cero y es el más simple vector espacial.
Una línea es un objeto unidimensional. Si escogemos un cierto vector distinto a cero en una cierta dirección, este vector tiene cierta longitud definida. Ese vector tiene una cabeza en un cierto punto en espacio y una cola en el origen. Si pensamos en estirar que ese vector así sea dos veces su largo, tres veces, etcétera y uniformemente, tomando todas las longitudes posibles (incluso la longitud cero, conseguir el vector cero), conseguiremos una sola línea con una sola dimensión: La de la longitud. Todos los vectores que describen puntos en esta línea serían paralelos. Aunque para visualizar la línea es necesario que ésta tenga un ancho mínimo, sin embargo, una línea de 1D no la tendría.
Un plano es un objeto de dos dimensiones. Tiene longitud y anchura pero no profundidad - algo como una hoja de papel, o más exactamente algo como las imágenes en un televisor común. El pensamiento en un plano en términos de vectores puede ser un poco más desafiante. Si pensamos en tomar un vector y lo movemos de modo que su cola esté tocando la cabeza del primero y esté formando un vector con su cola en el origen y la cabeza en la cabeza del segundo vector colocado de nuevo, tenemos una manera razonable de hablar de vectores de adición. Si tenemos dos vectores que no sean paralelos, podemos hablar de todos los puntos que podemos alcanzar por o solamente el estirar o ningunos de los vectores, y, agregando estos vectores juntos, estos puntos forman un plano.
El espacio, como lo percibimos, es tridimensional. Podemos pensar en poner una línea junto con un plano. Estas líneas son como un emparedado. Para conseguir a un cierto punto en espacio, podemos imaginarnos el viajar encima de la línea y después el movernos a través del plano al punto. Entonces tenemos tres vectores a pensar alrededor, uno a viajar una cierta distancia encima de la línea y dos para conseguir a un cierto punto en espacio.
Para tres rectas ortogonales en el espacio tridimensional (x, y y z) existe una cuarta, normal al espacio, ortogonal a estas tres rectas, que forma un eje p. ej. w.
El producto vectorial es la determinante de una matriz 4×4, donde una de las filas (o columnas) son los vectores unitarios h, i, j y k y las demás (filas o columnas respectivamente) están formadas por las componentes de tres vectores cuadradimensionales cualesquiera, este producto nos dará un cuarto vector perpendicular a estos tres mismos.
Geometría cuadridimensional en cuatro dimensiones espaciales[editar]
La Geometría euclidiana prevé una mayor variedad de formas para existir que en tres dimensiones. Los poliedros tridimensionales son recintos espaciales hechos de caras de dos dimensiones conectadas, los policronos cuadridimensionales son recintos del espacio cuadridimensional hechos de poliedros tridimensionales. Donde en tres dimensiones, hay exactamente cinco poliedros regulares, o los sólidos platónicos, que pueden existir, seis policronos regulares existen en la cuarta dimensión. Cinco de los seis se pueden interpretar como extensiones naturales de los sólidos platónicos, así como el cubo, un sólido platónico, es una extensión del cuadrado de dos dimensiones. El pentachoron está hecho de 5 tetraedros para las caras y 10 caras triangulares, y es el análogo cuadridimensional del tetraedro. El teseracto, o el hipercubo, se compone de 8 caras cúbicas y de 24 cuadrados, y es el politopo cuadridimensional medido. Los teseractos se doblan, la 16-celdas, son el equivalente del octaedro, pues son ambos politopos de cruz. Los politopos de 120 celdas y los de 600 celdas se doblan de igual modo, y son análogos al dodecaedro y al icosaedro, respectivamente. El de 24 celdas es un policrono regular único y que no tiene ningún equivalente tridimensional. Apenas pues la esfera, o 2-esfera, es una superficie de dos dimensiones curvada compuesta de todos los puntos equidistantes de un punto central dado, en un espacio tridimensional, la 3-esfera, una clase de hiperesfera, es el espacio que contiene todos los puntos equidistantes a un punto central dado, en un espacio cuadridimensional. Cada sección transversal tridimensional de un 3-esfera es un 2-esfera.
Analogía dimensional[editar]
La analogía dimensional se usa frecuentemente para comprender el salto de una dimensión (en este caso, la tercera dimensión) a una más alta (cuarta dimensión). La analogía dimensional consiste en resolver un problema en n + 1 dimensiones relacionándolo primero con un problema análogo de (n - 1) dimensión, vale decir, "una dimensión menos". E igualmente debe analizarse el caso de cómo se relaciona el problema en n con el de (n + 1) dimensiones, es decir, "una más".
Edwin Abbott Abbott en su libro Planilandia (Flatland) escribe sobre un "ser cuadrado" que vive en un mundo de dos dimensiones, como la superficie de un pedazo de papel. Este "cuadrado" se enfrenta a experimentos de un ser tridimensional. El ser tridimensional es percibido por el "cuadrado" como un ser aparentemente divino, ya que puede poner y quitar objetos de una caja fuerte sin romperla ni abrirla (moviéndolos a través de su tercera dimensión), ver todo desde de la perspectiva de dos dimensiones sea incluido detrás de las paredes (puesto que ve "sobre" Planilandia), y totalmente invisible para los habitantes de Planilandia, puesto que está "arriba" y una dimensión por arriba de las dos dimensiones en las que el cuadrado está atrapado. No obstante, el ser tridimensional podría manifestarse en el mundo de dos dimensiones, pero sólo parcialmente, si fuera una esfera, aparecería como una secuencia de círculos sucesivos "que cambian de tamaño" (intersecciones de la esfera con el plano de dos dimensiones). Aplicando analogía dimensional, uno puede deducir que el ser cuadridimensional sería capaz de hazañas similares de nuestra perspectiva tridimensional.
Rudy Rucker demuestra esto en su novela "Spaceland", en la cual el protagonista encuentra los seres cuadridimensionales que demuestran tales energías. Un uso útil de la analogía dimensional en visualizar la cuarta dimensión está en la proyección. Una proyección es una manera para representar un objeto (n+1)-dimensional en la n-dimensión. Por ejemplo, las pantallas de computadora son de dos dimensiones, y todas las fotografías de objetos tridimensionales son representadas en dos dimensiones puesto que la información de la tercera dimensión (o de la profundidad) no puede ser representada por la pantalla (si el observador se mueve, aleje o acerque, la imagen no cambiará). En este caso, la profundidad se quita y se substituye por la información indirecta. La retina del ojo es un arsenal de dos dimensiones de receptores pero puede permitir que el cerebro perciba la naturaleza de objetos tridimensionales usando la información indirecta (como la perspectiva, el sombreado, visión binocular, etc.).
La perspectiva del uso de los artistas da profundidad tridimensional a los cuadros de dos dimensiones. Asimismo, los objetos en la cuarta dimensión se pueden proyectar matemáticamente a las familiares tres dimensiones, donde pueden entonces ser examinados más convenientemente. En este caso, la "retina de un ojo cuadridimensional" tendría un arsenal de receptores tridimensionales. El ser hipotético con tal ojo percibiría la naturaleza de objetos cuadridimensionales usando la información indirecta contenida en las imágenes que recibe en su retina. La proyección de la perspectiva a partir de cuatro dimensiones produce efectos similares como en el caso tridimensional, tal como la perspectiva.
Esto agrega "profundidad cuadridimensional" a estos cuadros tridimensionales. La analogía dimensional también ayuda a entender tales proyecciones. Por ejemplo, los objetos de dos dimensiones son limitados por límites unidimensionales: un cuadrado es limitado por cuatro bordes o líneas. Los objetos tridimensionales son limitados por superficies de bidimensionales: un cubo es limitado por 6 cuadrados. Aplicando analogía dimensional, uno puede deducir que un cubo cuadridimensional, conocido como teseracto, es limitado por los volúmenes tridimensionales.
Y de hecho, éste es el caso matemáticamente: el teseracto es limitado por 8 cubos. Saber esto es indispensable para entender cómo interpretar una proyección tridimensional del teseracto. Los límites del teseracto proyectan a los volúmenes en la imagen, superficies no simplemente de dos dimensiones. Esto ayuda a entender las características de dichas dimensiones que de otra manera sólo confundirían. De igual manera, el concepto de sombras puede ayudarnos mejor a entender la teoría de cuatro dimensiones. Si usted proyectara una luz sobre objeto tridimensional, éste proyectaría una sombra de dos dimensiones. Por lo tanto la luz en un objeto de dos dimensiones echaría una sombra unidimensional (en un mundo de dos dimensiones), y la luz en un objeto unidimensional en un mundo unidimensional echaría una sombra cero-dimensional, es decir, un punto de la no-luz. Esta idea se puede utilizar en la otra dirección; la luz en un objeto cuadridimensional proyectaría una sombra tridimensional. Como ejemplo, la sombra de un cubo transparente, proyectaría una sombra sobre el papel, de dos cuadrados, unidos por sus vértices con 4 segmentos.
Semejantemente, si era un cubo cuadridimensional iluminado con luz de 4 dimensiones, su sombra sería la de un cubo tridimensional dentro de otro cubo tridimensional. Siendo tridimensionales podemos solamente ver el mundo con nuestros ojos en dos dimensiones; el ser cuadridimensional consideraría el mundo en tres. Así podría, por ejemplo, ver los seis lados de una caja opaca simultáneamente. No solamente eso; también podría ver lo que hay al interior de la caja, como en Planilandia, en donde la esfera ve objetos en el mundo de dos dimensiones y todo dentro de ellos simultáneamente. Análogo, un espectador cuadridimensional vería todos los puntos en nuestro espacio tridimensional simultáneamente, incluyendo la estructura interna de objetos sólidos y de cosas obscurecidos de nuestro punto de vista.
|
|
|
|
|
Cuarta Dimensión en física[editar]
Albert Einstein en su célebre teoría de 1905 de la relatividad especial habló por primera vez del tiempo como una cuarta dimensión y como algo indispensable para ubicar un objeto en el espacio y en un momento determinado. El tiempo en la teoría de la relatividad no es una dimensión espacial más, ya que fijado un punto del espacio-tiempo éste puede ser no alcanzable desde nuestra posición actual, hecho que difiere de la concepción usual de dimensión espacial. Aunque inicialmente se interpretó el tiempo como una "dimensión" matemática necesaria para ubicar un evento u objeto, en la teoría de la relatividad general el tiempo es tratado como una dimensión geométrica más, aunque los objetos materiales no puedan seguir una trayectoria completamente arbitraria a lo largo del tiempo (como por ejemplo "dar la vuelta" y viajar al pasado). La necesidad del tiempo dentro de la teoría de la relatividad es necesaria por dos motivos:
- En primer lugar, los objetos no sólo se mueven a través del espacio sino que también lo hacen a través del tiempo, es decir su coordenada temporal aumenta continuamente, por lo que hubo la necesidad de hablar del tiempo ligado al espacio como la cuarta dimensión (en inglés spacetime, en castellano espacio-tiempo). Además el ritmo de avance en la dimensión temporal depende del estado de movimiento del observador, produciéndose una dilatación temporal efectiva para los observadores más rápidos en relación al tiempo medido por un observador estacionario.
- En segundo lugar, el carácter intrínseco del espacio-tiempo y su cuatridimensionalidad requiere un modo conceptualmente diferente de tratar la geometría del universo, puesto que una cuarta dimensión implica un espacio plano (bidimensional) que se curva en la teoría de la relatividad general por la acción de la gravedad de la materia originándose la curvatura del espacio-tiempo.
Finalmente cabe añadir que algunas teorías físicas como la teoría de Kaluza-Klein y las teoría de supercuerdas, en sus varias versiones, añaden a las tres dimensiones físicas espaciales entre 1 y 9 dimensiones espaciales adicionales, de tipo compacto; además de la dimensión temporal.
Cuarta Dimensión en la Ciencia Ficción y la Cultura Popular[editar]
- La Cuarta Dimensión ha sido objeto de la fascinación popular desde los años 1920. Como "Into the Fourth Dimension" escrito por Ray Cummings en 1926, el cómic "Eugene the Jeep" o "-And He Built a Crooked House" por Robert A. Heinlein.
- Donnie Darko usa la cuarta dimensión como argumento para el viaje en el tiempo. La referencia se relaciona con el agua que es una cuarta herramienta dimensional para viajar del tiempo.
- Alan Moore en su novela gráfica "From Hell" utiliza la cuarta dimensión como referencia a la locura de Jack el Destripador.
- El juego Star Ocean: Till the End of Time usa la cuarta dimensión como realidad
- La película "Cube 2: Hypercube" (2002), la segunda en la serie de culto clásica de El Cubo, los personajes están atrapados en un teseracto con trampas y señuelos.
- Slaughterhouse-Five de Kurt Vonnegut caracteriza extraterrestres que existen entre Júpiter sus Lunas quienes lo referencian con la Cuarta Dimensión como el tiempo y el espacio
- El viajero del tiempo en "La Máquina del Tiempo" de H.G. Wells identifica el tiempo como la cuarta, así como el Doctor del primer episodio de Doctor Who.
- El videojuego Blinx: The Time Sweeper se refiere así mismo como "El primer juego de acción en 4D", con el jugador teniendo control sobre el flujo del tiempo del juego. Muchos otros juegos con habilidades de doblar el tiempo (como Prince of Persia: The Sands of the Time y Viewtiful Joe) o una coordinación interna del reloj (como Animal Crossing y Metal Gear Solid 3: Snake Eater) se les referencia como juegos en 4D.
- En la novela "A Wrinckle in Time", la cuarta dimensión representa el tiempo, como las tres primeras representan longitud, anchura y profundidad.
- En la serie de televisión Threshold, una raza extraterrestre quiénes están efectuando una invasión en la tierra - vinieron a conectar a tierra con las naves espaciales que intersecan la cuarta dimensión.
- Hay muchas referencias a la cuarta dimensión en el cine de ciencia ficción, en la trilogía "Volver al Futuro", Doc le dice a Marty "No estás pensando en la 4.ª dimensión" y le explica algo de ello.
- En "The Boy Who Reversed Himself," de William Sleator, los personajes principales se pierden en una cuarta dimensión espacial, donde encuentran a seres altamente inteligentes quienes se representa por 3 cruces dimensionales de ellos mismos, lo cual todos pueden ser percibidos en el libro de los personajes de tres dimensiones.
- En la novela "Coming Back Trought Time" de Michael Atkinson, prueba la grabación de la historia probando alrededor de sí mismo en orden para regresar a la cuarta dimensión.
- La mayoría de los simuladores utilizan el 4-D como término de comercialización.
- En el videojuego Mother, el personaje principal puede utilizar una capacidad especial de PK llamada "Fourth dimension slip" con la que sale inmediatamente de cualquier batalla.
- La novela "Diamond Dogs" del novelista Alastair Reynolds, los personajes deben solucionar enigmas y acertijos, algunos implican los objetos cuatridimensionales, esto para aventurarse más arriba de una estructura externa llamada "The Blood Spire".
- En la serie de televisión infantil Doraemon, el bolsillo mágico del mismo utiliza la cuarta dimensión para almacenar los inventos del futuro.
- EN la Pelicula Interstellar Se explica mucho acerca de esta dimension, llegando a representarla en un espacio tridimensional sobre el final del filme.
La cuarta dimensión en el Arte[editar]
La cuarta dimensión es un concepto que se puede encontrar repetidamente dentro de la distintas tendencias de las vanguardias artísticas de principios de siglo XX.[cita requerida] Este término fue incorporado al arte, influyendo a diversos artistas, gracias a la inquietud de matemáticos, artistas, filósofos y literatos que vieron en la cuarta dimensión la posibilidad de relativizar la exactitud de la ciencia y del conocimiento humano. Porque mas allá de la creencias paranormales o las ilusiones de la ciencia-ficción, la cuarta dimensión es un concepto que llevo al ser humano a seguir interrogándose sobre su papel en el universo, motivándolo a ver y entender el nuevo universo que se le estaba planteando.[2]
Referencias[editar]
- ↑ Michio Kaku, hyperspace, 1996.
- ↑ Arte americano: contextos y formas de ver. RIL editores. 2006. p. 311. ISBN 956-284-504-4.
Enlaces externos[editar]
Véase también[editar]
|
|
|
|
|
 Paolo Uccello antes del descubrimiento de America ya nos indicaba la forma de Toro
 |
Click para ampliar |
 Arte
 |
Click para ampliar |
 |
Click para ampliar |
Torta del Rey o roscon de Reyes
 |
Click para ampliar |
 El templo de Salomon o Sol-o-mon que esta inspirado en esto-
 |
Click para ampliar |
 La molecula de azufre octogonal utilizada en alquimia y las tantas Iglesias Romanicas y Templarias que hemos visto.
 |
Click para ampliar |
 Como se arreglan las moleculas de S8 rombico ? 
 |
Click para ampliar |
 Jardines del Taj Mahal
 |
Click para ampliar |
 Aljibe octogonal en el Taj Mahal- agua - Acuario  Tumba Taj Majal En fin los indicios estan alli para el que los busque, solo restaba atar los cabos. Por ejemplo con la granada del Cristo de Da Vinci, vamos a buscar la forma de la granada y resulta que sus semillas forman un rombododecaedro, se llama granada por analogia del cristal de granate que tambien tiene esa forma, continuando con las analogias tenemos la granada explosiva por que es en esta forma que la galaxia explota. Buscando formas del hipercubo encontramos el rombododecaedro, por lo cual tenemos el indicio de que esta forma es especial. Descomponemos esta figura en dos cubos, y asignamos las coordenadas binarias y tenemos el diagrama, vemos que el 6 y el 9 que son espirales geometricos coinciden en un punto medio lo cual indica un claro choque o rebote ya que hay contacto. Nos falta entonces interpretar el eje w sobre el cual se mueven los cubos, que es el espiral que se come la cola, me llevo unos meses descifrarlo, pero el codigo esta por todos lados como hemos visto. Superponemos la figura al Zodiaco y tenemos un mapeo, ademas en base a su construccion podemos descifrar el siginificado de la gran Piramide, el obelisco, que surgen de los ciclos pentagonales y heptagonales. Atando cabos, vamos armando el puzzle, sin mas misterios. The Six Cornered SnowflakeEn el copo de nieve de seis ángulos Ensayo de Kepler, "En el copo de nieve de seis ángulos", es considerado como el primer trabajo que analiza y describe la estructura de los cristales.
Última edición por IndigoMerovingio; 14-abr-2012 a las 04:31
|
|
|
|
|
| |
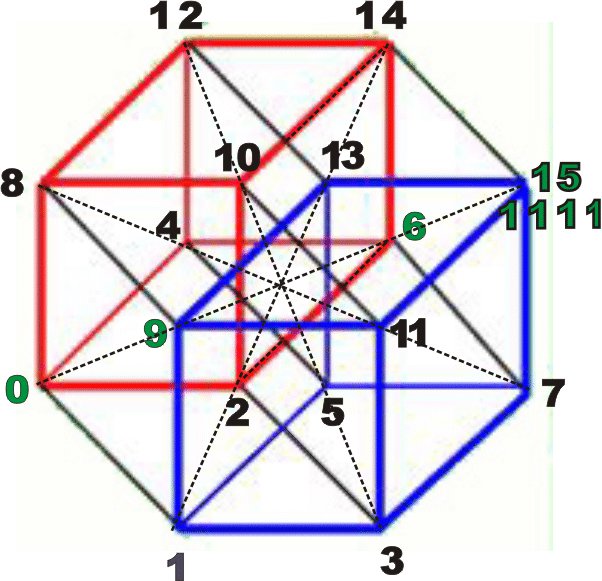
Yes, we now need Metatron to get hype (hypercube) to help us all look deeper.  The cubes could be fractal, therefor could reveal more cubes inside of that 4D tesseract we call life. We are the 1, and the 37 affects us through color/frequency (sacred rays) which comes from different zones/ cones of the zodiac. I believe the stars are our connection to the creator through ways heard but not seen and vice versa. Could we relate the number 64 to whats beyond the cosmos of 37? Whats are your thoughts on this? http://www.msnbc.msn.com/id/34845772/ns ... -detected/ http://www.lunarplanner.com/Harmonics/p ... onics.htmlMetatrons Cube or 4D Hypercube http://www.lunarplanner.com/Harmonics/p ... onics.htmlMetatrons Cube or 4D Hypercube   What could this circle inside of the cube represent   The Fourth Dimension could be our reality. In 4D there are a infinite number of solids (expansion beyond the platonic solids) in the Universe are in relationship with each other through time and energy. In this time domain, 4D continues the movement of the 3D (Past) to form a wave (an S), constituting fractally in the space-time continuum. Sine wave? Earth travels on this wave as we move through our zodiac.  As above, so below  The hypercube (4D) could be viewed geometrically by fractals. Also, the hypercube is the symbol used in mathematics to try and represent the fourth dimension in two dimensions (a drawing on a piece of paper - a plane, not the ones that fly).  The Hypercube is cut by 4 diagonals constituting the central point (us). This center point could represent the identity or the pure self. The number of the diagonals is 4 X 3 = 9, according to the Pythagorean theorem. The four diagonals are 1-5, 2-6, 3-7 and 4-0. It is my opinion that each of those 4 diagonals represent something glorious about our nature. Ether (sphere's of rhombic dodecahedra) are at work through these movements. 4(rhombus) x 12(dodecahedron) = 48 which also relates with the heavenly body's. http://www.biblewheel.com/gr/gr_48.asphttp://www.mathsisfun.com/geometry/dodecahedron.html / http://en.wikipedia.org/wiki/Rhombic_dodecahedronThrough all this we have to remember that the smallest possible mathematical cube is 27(earth). Lets look more into all this Raph.
|
|
|
|
|
|
|
 Dome of the Rock The floor plan of the Dome of the Rock and some construction lines; possible source of inspiration for Templar constructions and the cross pathee
_________________
Everything is Connected and there are no
coincidences
|
|
Centered octagonal number
From Wikipedia, the free encyclopedia
A centered octagonal number is a centered figurate number that represents an octagon with a dot in the center and all other dots surrounding the center dot in successive octagonal layers.[1] The centered octagonal numbers are the same as the odd square numbers.[2] Thus, the nth centered octagonal number is given by the formula
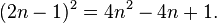
The first few centered octagonal numbers are[2]
- 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089.
Calculating Ramanujan's tau function on a centered octagonal number yields an odd number, whereas for any other number the function yields an even number.[2]
See also[edit]
References[edit]
https://en.wikipedia.org/wiki/Centered_octagonal_number
The New Jerusalem Diagram – Introduction
“The New Jerusalem Diagram” is the name given by the scholar of ancient lore, John Michell [The original explanations in John Michell's books, especially "The Dimensions of Paradise", Thames and Hudson, 1986] to a geometrical construction that allows the “squaring of the circle” and the division of the circle to 28 equal sectors (a zodiac wheel) and the ceremonial positioning of the twelve tribes (or constellations) in a pattern of four camps at the four sides of the square.
John Michell has reconstructed the geometric pattern of the ‘heavenly city’ which is the template of the New Jerusalem of Revelation 21.

He discovered that this diagram served as the design (blueprint) for many sacred sites, including the Stonehenge, The Great Pyramid, St. Mary’s Chapel at Glastonbury and the City of Magnesia in Plato’s The Laws.

The Great Pyramid, Earth and Moon fit the New Jerusalem Diagram
It turns out that also the Nazca glyph called “Mandala” aka “Sun-Star-Cross” perfectly matches the New Jerusalem Diagram.



Superimposed image of NJ Diagram and Mandala glyph near Nazca, Peru
It is no surprise that the NJ diagram matches blueprint for the The Dome of the Rock, a shrine located on the Temple Mount in the Old City of Jerusalem.

The wheel of 28 divisions is common to various esoteric systems and serves as representation for the schematic month: 4 weeks = 28 days. The solar calendar of the Dead Sea scrolls sect was of 364 days, which is a multiple of 28 ( 28×13 = 364). In many Sufi diagrams, including in the ceiling of the dome at the El-Aqsa Mosque* (not the Dome of the Rock) at the Temple Mount, there appears the motif of the wheel made of 28 divisions.

Al-Aqsa. The resplendent ceiling of the Al-Aqsa Mosque on the Temple Mount in Jerusalem. The mosque, one of Islam’s most holy sites, sits near the Dome of the Rock and above the Marwani Mosque, aka Solomon’s Stables.
Image Source/Credit.
The NJ diagram is also hinted and enfolded (according to Micheell), in the description of the holy city, The New Jerusalem, whose descent from heaven concludes the Christian Bible.

Below we present 3-D version of the New Jerusalem Diagram.

Is it possible the 3D NJ diagram was used as a blueprint for the Crown Jewels?… Perhaps this is a case of a “secret hidden in plain site”?


The collective term Crown Jewels denotes the regalia and vestments worn by the sovereign of the United Kingdom during the coronation ceremony and at other state functions. The term refers to the following objects: the crowns, sceptres (with either the cross or the dove), orbs, swords, rings, spurs, colobium sindonis, dalmatic, armill, and the royal robe or pall, as well as several other objects connected with the ceremony itself. The Crown Jewels have a religious and sacral connotation. Their hidden symbolism seems to be related to the sacred geometry of the New Jerusalem Diagram.
The Construction of the New Jerusalem Diagram
The construction of this diagram starts with the attempt to “square the circle” by drawing a circle and a square that have the same circumference.
- So in building this sacred diagram, one starts with a circle with a diameter of 22 units, and blocks it with a square of 22 x 22 units (like the number of the Hebrew letters, with which supposedly “heaven and earth were made”).
- Then one draws from the same centre an additional circle whose diameter is 28 units – “the perfect number” that is already the number of the letters in the first verse of genesis and marks the circle of the seasons. The circle with diameter 28 has circumference of Pi x 28, which is as noted 22/7 x 28 = 88 – just the circumference of the square with edges of 22 and circumference thus 2 x 22 = 88.
The circle and the square have the same circumference, and they intersect in 8 points, where the square juts out of the circle in 4 vertices.

- The building of the complete pattern continues with the drawing of 12 circles with diameter of 6 units – the number of letters in the first word of Genesis – Bereshit – as the first “perfect number”. The centers of these twelve circles are situated on the outer big circle, whose diameter is 28, and they touch (are tangent to) the inner circle, whose diameter is 22. Four of these circles are situated according to the points were the square is tangent to the inner circle, and the other 8 circles are placed according to the 8 points of intersection between the square and the outer circle.

There are two amazing consequences of this construction:
- This construction squares the circle
- It divides the circle into 28 equal segments
- It reflects ratio 22:7 which is good approximation of the “Pi”
- It reflects golden ratio 1.618
- It reflects the ratio of 22:6, which issues theoretical-geometrical considerations is also the exact real ratio between the diameter of the earth and the diameter of the moon!

There are many more features of the NJ diagram which will be presented in our upcoming articles (e.g. amazing connection with Teotihuacan).
|
|
|
|
|
|
|
|
El término cuarta dimensión aparece en diversos contextos como la física, las matemáticas y la ciencia ficción. En cada contexto el significado es diferente:
En física, se hace referencia a la cuarta dimensión al hablar del tiempo, principalmente desde el planteamiento de la Teoría de la Relatividad.
En matemática, el concepto aparece asociado o bien a espacios euclídeos de más de tres dimensiones o, más generalmente, a espacios localmente euclídeos o 4-variedades diferenciables.

Hipercubo de 4 dimensiones espaciales girando, tal como se vería proyectado en el espacio tridimensional.
El interés en las dimensiones más altas alcanzó su clímax entre 1870 y 1920.1 En esos años se convirtió en tema frecuente en la literatura fantástica, el arte e incluso algunas teorías científicas. La cuarta dimensión, entendida como dimensión espacial adicional (no como dimensión temporal, como en la teoría de la relatividad) apareció en las obras literarias de Oscar Wilde, Fiódor Dostoyevski, Marcel Proust, H. G. Wells y Joseph Conrad, inspiró algunas obras musicales de Alexander Scriabin, Edgar Varèse y George Antheil y algunas obras plásticas de Pablo Picasso y Marcel Duchamp influyendo en el desarrollo del cubismo. Incluso personajes tan diversos como el psicólogo William James, la escritora Gertrude Stein o el socialista revolucionario Vladimir Lenin se interesaron en el tema.
Igualmente los matemáticos habían estado interesados en el tema al tratar de generalizar los conceptos de la geometría euclídea tridimensional. El matemático Charles L. Dodgson, que enseñó en la Universidad de Oxford, deleitó a generaciones de escolares escribiendo libros, bajo el pseudónimo de Lewis Carroll, que incorporaban algunas ideas sobre la cuarta dimensión. Desde el punto de vista académico, el estudio general de la geometría de la cuarta dimensión en gran parte resultado de los trabajos de Bernhard Riemann. Charles Howard Hinton, matemático y escritor de ciencia ficción británico, acuñó muchos neologismos para describir elementos en la cuarta dimensión. De acuerdo con el Oxford English Dictionary, fue el primero en emplear la palabra tesseract en su libro Una nueva era del pensamiento. También inventó las palabras “kata” (del griego “abajo”) y “ana” (del griego “arriba”) para describir las dos direcciones opuestas en la cuarta dimensión, equivalentes a derecha-izquierda, arriba-abajo, y adelante-atrás.
Los trabajos matemáticos sobre geometrías multidimensionales y geometrías no euclídeas habían sido considerado por los físicos como simples abstracciones matemáticas hasta que Henri Poincaré probó que el grupo de transformaciones de Lorentz que dejaban invariantes las ecuaciones del electromagnetismo podían ser interpretadas como "rotaciones" en un espacio de cuatro dimensiones. Más tarde, los trabajos de Einstein y la interpretación geométrica de estos por parte de Hermann Minkowski llevaron a la aceptación de la cuarta dimensión como una descripción necesaria para explicar los hechos observados relacionados con el electromagnetismo. Sin embargo, aquí la "cuarta dimensión" no era un lugar separado del espacio tridimensional (como en varias de las obras de ficción de la época) ni tampoco una dimensión espacial análoga a las otras tres dimensiones espaciales, sino una dimensión temporal que sólo puede recorrerse hacia el futuro. En la teoría general de la relatividad el campo gravitatorio es explicado como un efecto geométrico de la curvatura de un espacio-tiempo de cuatro dimensiones.
Más tarde, la teoría de Kaluza-Klein propuso que no sólo el campo gravitatorio podía ser interpretado de forma más sencilla como curvatura de un "espacio" de más de tres dimensiones, sino que si se introducía una nueva dimensión espacial enrollada o «compactificada», también el campo electromagnético podía ser interpretado como un efecto geométrico de la curvatura de dimensiones superiores. Así, la Kaluza proponía una teoría de campo unificado del electromagnetismo y la gravedad en un espacio-tiempo de cinco dimensiones, con una dimensión temporal, tres dimensiones espaciales extendidas y una dimensión espacial «compactificada» adicional, que, debido a su condición de compactificada, no era directamente visible pero su efecto era perceptible en forma de campo electromagnético.

Un ángulo recto se describe como un cuarto de una revolución. La Geometría Cartesiana escoge direcciones ortogonales arbitrariamente a través del espacio, lo que significa que cada dirección está en ángulo recto con las demás. Las 3 dimensiones ortogonales del espacio se conocen como altitud, longitud y latitud. La Cuarta Dimensión por lo tanto es la dirección en el espacio con ángulo recto a las 3 direcciones observables.
Un vector espacial es un conjunto de vectores, los cuales podemos imaginarlos como flechas, que proviene de un simple lugar llamado origen (vectores geométricos), que apuntan a otros lugares.
Un punto es un objeto de cero dimensiones. No tiene extensión en el espacio ni propiedades, como una flecha pero sin longitud. Este vector es llamado el vector cero y es el más simple vector espacial.
Una línea es un objeto unidimensional. Si escogemos un cierto vector distinto a cero en una cierta dirección, este vector tiene cierta longitud definida. Ese vector tiene una cabeza en un cierto punto en espacio y una cola en el origen. Si pensamos en estirar que ese vector así sea dos veces su largo, tres veces, etcétera y uniformemente, tomando todas las longitudes posibles (incluso la longitud cero, conseguir el vector cero), conseguiremos una sola línea con una sola dimensión: La de la longitud. Todos los vectores que describen puntos en esta línea serían paralelos. Aunque para visualizar la línea es necesario que ésta tenga un ancho mínimo, sin embargo, una línea de 1D no la tendría.
Un plano es un objeto de dos dimensiones. Tiene longitud y anchura pero no profundidad - algo como una hoja de papel, o más exactamente algo como las imágenes en un televisor común. El pensamiento en un plano en términos de vectores puede ser un poco más desafiante. Si pensamos en tomar un vector y lo movemos de modo que su cola esté tocando la cabeza del primero y esté formando un vector con su cola en el origen y la cabeza en la cabeza del segundo vector colocado de nuevo, tenemos una manera razonable de hablar de vectores de adición. Si tenemos dos vectores que no sean paralelos, podemos hablar de todos los puntos que podemos alcanzar por o solamente el estirar o ningunos de los vectores, y, agregando estos vectores juntos, estos puntos forman un plano.
El espacio, como lo percibimos, es tridimensional. Podemos pensar en poner una línea junto con un plano. Estas líneas son como un emparedado. Para conseguir a un cierto punto en espacio, podemos imaginarnos el viajar encima de la línea y después el movernos a través del plano al punto. Entonces tenemos tres vectores a pensar alrededor, uno a viajar una cierta distancia encima de la línea y dos para conseguir a un cierto punto en espacio.
Para tres rectas ortogonales en el espacio tridimensional (x, y y z) existe una cuarta, normal al espacio, ortogonal a estas tres rectas, que forma un eje p. ej. w.
El producto vectorial es la determinante de una matriz 4×4, donde una de las filas (o columnas) son los vectores unitarios h, i, j y k y las demás (filas o columnas respectivamente) están formadas por las componentes de tres vectores cuadradimensionales cualesquiera, este producto nos dará un cuarto vector perpendicular a estos tres mismos.
La Geometría euclidiana prevé una mayor variedad de formas para existir que en tres dimensiones. Los poliedros tridimensionales son recintos espaciales hechos de caras de dos dimensiones conectadas, los policronos cuadridimensionales son recintos del espacio cuadridimensional hechos de poliedros tridimensionales. Donde en tres dimensiones, hay exactamente cinco poliedros regulares, o los sólidos platónicos, que pueden existir, seis policronos regulares existen en la cuarta dimensión. Cinco de los seis se pueden interpretar como extensiones naturales de los sólidos platónicos, así como el cubo, un sólido platónico, es una extensión del cuadrado de dos dimensiones. El pentachoron está hecho de 5 tetraedros para las caras y 10 caras triangulares, y es el análogo cuadridimensional del tetraedro. El teseracto, o el hipercubo, se compone de 8 caras cúbicas y de 24 cuadrados, y es el politopo cuadridimensional medido. Los teseractos se doblan, la 16-celdas, son el equivalente del octaedro, pues son ambos politopos de cruz. Los politopos de 120 celdas y los de 600 celdas se doblan de igual modo, y son análogos al dodecaedro y al icosaedro, respectivamente. El de 24 celdas es un policrono regular único y que no tiene ningún equivalente tridimensional. Apenas pues la esfera, o 2-esfera, es una superficie de dos dimensiones curvada compuesta de todos los puntos equidistantes de un punto central dado, en un espacio tridimensional, la 3-esfera, una clase de hiperesfera, es el espacio que contiene todos los puntos equidistantes a un punto central dado, en un espacio cuadridimensional. Cada sección transversal tridimensional de un 3-esfera es un 2-esfera.

La analogía dimensional se usa frecuentemente para comprender el salto de una dimensión (en este caso, la tercera dimensión) a una más alta (cuarta dimensión). La analogía dimensional consiste en resolver un problema en n + 1 dimensiones relacionándolo primero con un problema análogo de (n - 1) dimensión, vale decir, "una dimensión menos". E igualmente debe analizarse el caso de cómo se relaciona el problema en n con el de (n + 1) dimensiones, es decir, "una más".
Edwin Abbott Abbott en su libro Planilandia (Flatland) escribe sobre un "ser cuadrado" que vive en un mundo de dos dimensiones, como la superficie de un pedazo de papel. Este "cuadrado" se enfrenta a experimentos de un ser tridimensional. El ser tridimensional es percibido por el "cuadrado" como un ser aparentemente divino, ya que puede poner y quitar objetos de una caja fuerte sin romperla ni abrirla (moviéndolos a través de su tercera dimensión), ver todo desde de la perspectiva de dos dimensiones sea incluido detrás de las paredes (puesto que ve "sobre" Planilandia), y totalmente invisible para los habitantes de Planilandia, puesto que está "arriba" y una dimensión por arriba de las dos dimensiones en las que el cuadrado está atrapado. No obstante, el ser tridimensional podría manifestarse en el mundo de dos dimensiones, pero sólo parcialmente, si fuera una esfera, aparecería como una secuencia de círculos sucesivos "que cambian de tamaño" (intersecciones de la esfera con el plano de dos dimensiones). Aplicando analogía dimensional, uno puede deducir que el ser cuadridimensional sería capaz de hazañas similares de nuestra perspectiva tridimensional.
Rudy Rucker demuestra esto en su novela "Spaceland", en la cual el protagonista encuentra los seres cuadridimensionales que demuestran tales energías. Un uso útil de la analogía dimensional en visualizar la cuarta dimensión está en la proyección. Una proyección es una manera para representar un objeto (n+1)-dimensional en la n-dimensión. Por ejemplo, las pantallas de computadora son de dos dimensiones, y todas las fotografías de objetos tridimensionales son representadas en dos dimensiones puesto que la información de la tercera dimensión (o de la profundidad) no puede ser representada por la pantalla (si el observador se mueve, aleje o acerque, la imagen no cambiará). En este caso, la profundidad se quita y se substituye por la información indirecta. La retina del ojo es un arsenal de dos dimensiones de receptores pero puede permitir que el cerebro perciba la naturaleza de objetos tridimensionales usando la información indirecta (como la perspectiva, el sombreado, visión binocular, etc.).
La perspectiva del uso de los artistas da profundidad tridimensional a los cuadros de dos dimensiones. Asimismo, los objetos en la cuarta dimensión se pueden proyectar matemáticamente a las familiares tres dimensiones, donde pueden entonces ser examinados más convenientemente. En este caso, la "retina de un ojo cuadridimensional" tendría un arsenal de receptores tridimensionales. El ser hipotético con tal ojo percibiría la naturaleza de objetos cuadridimensionales usando la información indirecta contenida en las imágenes que recibe en su retina. La proyección de la perspectiva a partir de cuatro dimensiones produce efectos similares como en el caso tridimensional, tal como la perspectiva.
Esto agrega "profundidad cuadridimensional" a estos cuadros tridimensionales. La analogía dimensional también ayuda a entender tales proyecciones. Por ejemplo, los objetos de dos dimensiones son limitados por límites unidimensionales: un cuadrado es limitado por cuatro bordes o líneas. Los objetos tridimensionales son limitados por superficies de bidimensionales: un cubo es limitado por 6 cuadrados. Aplicando analogía dimensional, uno puede deducir que un cubo cuadridimensional, conocido como teseracto, es limitado por los volúmenes tridimensionales.
Y de hecho, éste es el caso matemáticamente: el teseracto es limitado por 8 cubos. Saber esto es indispensable para entender cómo interpretar una proyección tridimensional del teseracto. Los límites del teseracto proyectan a los volúmenes en la imagen, superficies no simplemente de dos dimensiones. Esto ayuda a entender las características de dichas dimensiones que de otra manera sólo confundirían. De igual manera, el concepto de sombras puede ayudarnos mejor a entender la teoría de cuatro dimensiones. Si usted proyectara una luz sobre objeto tridimensional, éste proyectaría una sombra de dos dimensiones. Por lo tanto la luz en un objeto de dos dimensiones echaría una sombra unidimensional (en un mundo de dos dimensiones), y la luz en un objeto unidimensional en un mundo unidimensional echaría una sombra cero-dimensional, es decir, un punto de la no-luz. Esta idea se puede utilizar en la otra dirección; la luz en un objeto cuadridimensional proyectaría una sombra tridimensional. Como ejemplo, la sombra de un cubo transparente, proyectaría una sombra sobre el papel, de dos cuadrados, unidos por sus vértices con 4 segmentos.
Semejantemente, si era un cubo cuadridimensional iluminado con luz de 4 dimensiones, su sombra sería la de un cubo tridimensional dentro de otro cubo tridimensional. Siendo tridimensionales podemos solamente ver el mundo con nuestros ojos en dos dimensiones; el ser cuadridimensional consideraría el mundo en tres. Así podría, por ejemplo, ver los seis lados de una caja opaca simultáneamente. No solamente eso; también podría ver lo que hay al interior de la caja, como en Planilandia, en donde la esfera ve objetos en el mundo de dos dimensiones y todo dentro de ellos simultáneamente. Análogo, un espectador cuadridimensional vería todos los puntos en nuestro espacio tridimensional simultáneamente, incluyendo la estructura interna de objetos sólidos y de cosas obscurecidos de nuestro punto de vista.
Albert Einstein en su célebre teoría de 1905 de la relatividad especial habló por primera vez del tiempo como una cuarta dimensión y como algo indispensable para ubicar un objeto en el espacio y en un momento determinado. El tiempo en la teoría de la relatividad no es una dimensión espacial más, ya que fijado un punto del espacio-tiempo éste puede ser no alcanzable desde nuestra posición actual, hecho que difiere de la concepción usual de dimensión espacial. Aunque inicialmente se interpretó el tiempo como una "dimensión" matemática necesaria para ubicar un evento u objeto, en la teoría de la relatividad general el tiempo es tratado como una dimensión geométrica más, aunque los objetos materiales no puedan seguir una trayectoria completamente arbitraria a lo largo del tiempo (como por ejemplo "dar la vuelta" y viajar al pasado). La necesidad del tiempo dentro de la teoría de la relatividad es necesaria por dos motivos:
En primer lugar, los objetos no sólo se mueven a través del espacio sino que también lo hacen a través del tiempo, es decir su coordenada temporal aumenta continuamente, por lo que hubo la necesidad de hablar del tiempo ligado al espacio como la cuarta dimensión (en inglés spacetime, en castellano espacio-tiempo). Además el ritmo de avance en la dimensión temporal depende del estado de movimiento del observador, produciéndose una dilatación temporal efectiva para los observadores más rápidos en relación al tiempo medido por un observador estacionario.
En segundo lugar, el carácter intrínseco del espacio-tiempo y su cuatridimensionalidad requiere un modo conceptualmente diferente de tratar la geometría del universo, puesto que una cuarta dimensión implica un espacio plano (bidimensional) que se curva en la teoría de la relatividad general por la acción de la gravedad de la materia originándose la curvatura del espacio-tiempo.
Finalmente cabe añadir que algunas teorías físicas como la teoría de Kaluza-Klein y las teoría de supercuerdas, en sus varias versiones, añaden a las tres dimensiones físicas espaciales entre 1 y 9 dimensiones espaciales adicionales, de tipo compacto; además de la dimensión temporal.
|
|
|
|
|

es.walyou.com
2 Alcancia cubo Rubik
521 × 423 - 24k - jpg |

es.wikipedia.org
El interior de un cubo de
232 × 199 - 28k - jpg |

solostocks.com
Cubo Mágico
500 × 500 - 29k - jpg |

pocoseso.com
del Rubik - Cubo Magico -
450 × 338 - 28k - jpg |
Búsquedas relacionadas con cubo magico
EL MISMO "CUBO MAGICO" ES UN HIPERCUBO (HAY UN CUBO MAS CHICO EN EL CENTRO DEL MISMO)
| Reply |
Message 24 of 24 on the subject |
|
El término cuarta dimensión aparece en diversos contextos como la física, las matemáticas y la ciencia ficción. En cada contexto el significado es diferente:
En física, se hace referencia a la cuarta dimensión al hablar del tiempo, principalmente desde el planteamiento de la Teoría de la Relatividad.
En matemática, el concepto aparece asociado o bien a espacios euclídeos de más de tres dimensiones o, más generalmente, a espacios localmente euclídeos o 4-variedades diferenciables.

Hipercubo de 4 dimensiones espaciales girando, tal como se vería proyectado en el espacio tridimensional.
El interés en las dimensiones más altas alcanzó su clímax entre 1870 y 1920.1 En esos años se convirtió en tema frecuente en la literatura fantástica, el arte e incluso algunas teorías científicas. La cuarta dimensión, entendida como dimensión espacial adicional (no como dimensión temporal, como en la teoría de la relatividad) apareció en las obras literarias de Oscar Wilde, Fiódor Dostoyevski, Marcel Proust, H. G. Wells y Joseph Conrad, inspiró algunas obras musicales de Alexander Scriabin, Edgar Varèse y George Antheil y algunas obras plásticas de Pablo Picasso y Marcel Duchamp influyendo en el desarrollo del cubismo. Incluso personajes tan diversos como el psicólogo William James, la escritora Gertrude Stein o el socialista revolucionario Vladimir Lenin se interesaron en el tema.
Igualmente los matemáticos habían estado interesados en el tema al tratar de generalizar los conceptos de la geometría euclídea tridimensional. El matemático Charles L. Dodgson, que enseñó en la Universidad de Oxford, deleitó a generaciones de escolares escribiendo libros, bajo el pseudónimo de Lewis Carroll, que incorporaban algunas ideas sobre la cuarta dimensión. Desde el punto de vista académico, el estudio general de la geometría de la cuarta dimensión en gran parte resultado de los trabajos de Bernhard Riemann. Charles Howard Hinton, matemático y escritor de ciencia ficción británico, acuñó muchos neologismos para describir elementos en la cuarta dimensión. De acuerdo con el Oxford English Dictionary, fue el primero en emplear la palabra tesseract en su libro Una nueva era del pensamiento. También inventó las palabras “kata” (del griego “abajo”) y “ana” (del griego “arriba”) para describir las dos direcciones opuestas en la cuarta dimensión, equivalentes a derecha-izquierda, arriba-abajo, y adelante-atrás.
Los trabajos matemáticos sobre geometrías multidimensionales y geometrías no euclídeas habían sido considerado por los físicos como simples abstracciones matemáticas hasta que Henri Poincaré probó que el grupo de transformaciones de Lorentz que dejaban invariantes las ecuaciones del electromagnetismo podían ser interpretadas como "rotaciones" en un espacio de cuatro dimensiones. Más tarde, los trabajos de Einstein y la interpretación geométrica de estos por parte de Hermann Minkowski llevaron a la aceptación de la cuarta dimensión como una descripción necesaria para explicar los hechos observados relacionados con el electromagnetismo. Sin embargo, aquí la "cuarta dimensión" no era un lugar separado del espacio tridimensional (como en varias de las obras de ficción de la época) ni tampoco una dimensión espacial análoga a las otras tres dimensiones espaciales, sino una dimensión temporal que sólo puede recorrerse hacia el futuro. En la teoría general de la relatividad el campo gravitatorio es explicado como un efecto geométrico de la curvatura de un espacio-tiempo de cuatro dimensiones.
Más tarde, la teoría de Kaluza-Klein propuso que no sólo el campo gravitatorio podía ser interpretado de forma más sencilla como curvatura de un "espacio" de más de tres dimensiones, sino que si se introducía una nueva dimensión espacial enrollada o «compactificada», también el campo electromagnético podía ser interpretado como un efecto geométrico de la curvatura de dimensiones superiores. Así, la Kaluza proponía una teoría de campo unificado del electromagnetismo y la gravedad en un espacio-tiempo de cinco dimensiones, con una dimensión temporal, tres dimensiones espaciales extendidas y una dimensión espacial «compactificada» adicional, que, debido a su condición de compactificada, no era directamente visible pero su efecto era perceptible en forma de campo electromagnético.

Un ángulo recto se describe como un cuarto de una revolución. La Geometría Cartesiana escoge direcciones ortogonales arbitrariamente a través del espacio, lo que significa que cada dirección está en ángulo recto con las demás. Las 3 dimensiones ortogonales del espacio se conocen como altitud, longitud y latitud. La Cuarta Dimensión por lo tanto es la dirección en el espacio con ángulo recto a las 3 direcciones observables.
Un vector espacial es un conjunto de vectores, los cuales podemos imaginarlos como flechas, que proviene de un simple lugar llamado origen (vectores geométricos), que apuntan a otros lugares.
Un punto es un objeto de cero dimensiones. No tiene extensión en el espacio ni propiedades, como una flecha pero sin longitud. Este vector es llamado el vector cero y es el más simple vector espacial.
Una línea es un objeto unidimensional. Si escogemos un cierto vector distinto a cero en una cierta dirección, este vector tiene cierta longitud definida. Ese vector tiene una cabeza en un cierto punto en espacio y una cola en el origen. Si pensamos en estirar que ese vector así sea dos veces su largo, tres veces, etcétera y uniformemente, tomando todas las longitudes posibles (incluso la longitud cero, conseguir el vector cero), conseguiremos una sola línea con una sola dimensión: La de la longitud. Todos los vectores que describen puntos en esta línea serían paralelos. Aunque para visualizar la línea es necesario que ésta tenga un ancho mínimo, sin embargo, una línea de 1D no la tendría.
Un plano es un objeto de dos dimensiones. Tiene longitud y anchura pero no profundidad - algo como una hoja de papel, o más exactamente algo como las imágenes en un televisor común. El pensamiento en un plano en términos de vectores puede ser un poco más desafiante. Si pensamos en tomar un vector y lo movemos de modo que su cola esté tocando la cabeza del primero y esté formando un vector con su cola en el origen y la cabeza en la cabeza del segundo vector colocado de nuevo, tenemos una manera razonable de hablar de vectores de adición. Si tenemos dos vectores que no sean paralelos, podemos hablar de todos los puntos que podemos alcanzar por o solamente el estirar o ningunos de los vectores, y, agregando estos vectores juntos, estos puntos forman un plano.
El espacio, como lo percibimos, es tridimensional. Podemos pensar en poner una línea junto con un plano. Estas líneas son como un emparedado. Para conseguir a un cierto punto en espacio, podemos imaginarnos el viajar encima de la línea y después el movernos a través del plano al punto. Entonces tenemos tres vectores a pensar alrededor, uno a viajar una cierta distancia encima de la línea y dos para conseguir a un cierto punto en espacio.
Para tres rectas ortogonales en el espacio tridimensional (x, y y z) existe una cuarta, normal al espacio, ortogonal a estas tres rectas, que forma un eje p. ej. w.
El producto vectorial es la determinante de una matriz 4×4, donde una de las filas (o columnas) son los vectores unitarios h, i, j y k y las demás (filas o columnas respectivamente) están formadas por las componentes de tres vectores cuadradimensionales cualesquiera, este producto nos dará un cuarto vector perpendicular a estos tres mismos.
La Geometría euclidiana prevé una mayor variedad de formas para existir que en tres dimensiones. Los poliedros tridimensionales son recintos espaciales hechos de caras de dos dimensiones conectadas, los policronos cuadridimensionales son recintos del espacio cuadridimensional hechos de poliedros tridimensionales. Donde en tres dimensiones, hay exactamente cinco poliedros regulares, o los sólidos platónicos, que pueden existir, seis policronos regulares existen en la cuarta dimensión. Cinco de los seis se pueden interpretar como extensiones naturales de los sólidos platónicos, así como el cubo, un sólido platónico, es una extensión del cuadrado de dos dimensiones. El pentachoron está hecho de 5 tetraedros para las caras y 10 caras triangulares, y es el análogo cuadridimensional del tetraedro. El teseracto, o el hipercubo, se compone de 8 caras cúbicas y de 24 cuadrados, y es el politopo cuadridimensional medido. Los teseractos se doblan, la 16-celdas, son el equivalente del octaedro, pues son ambos politopos de cruz. Los politopos de 120 celdas y los de 600 celdas se doblan de igual modo, y son análogos al dodecaedro y al icosaedro, respectivamente. El de 24 celdas es un policrono regular único y que no tiene ningún equivalente tridimensional. Apenas pues la esfera, o 2-esfera, es una superficie de dos dimensiones curvada compuesta de todos los puntos equidistantes de un punto central dado, en un espacio tridimensional, la 3-esfera, una clase de hiperesfera, es el espacio que contiene todos los puntos equidistantes a un punto central dado, en un espacio cuadridimensional. Cada sección transversal tridimensional de un 3-esfera es un 2-esfera.

La analogía dimensional se usa frecuentemente para comprender el salto de una dimensión (en este caso, la tercera dimensión) a una más alta (cuarta dimensión). La analogía dimensional consiste en resolver un problema en n + 1 dimensiones relacionándolo primero con un problema análogo de (n - 1) dimensión, vale decir, "una dimensión menos". E igualmente debe analizarse el caso de cómo se relaciona el problema en n con el de (n + 1) dimensiones, es decir, "una más".
Edwin Abbott Abbott en su libro Planilandia (Flatland) escribe sobre un "ser cuadrado" que vive en un mundo de dos dimensiones, como la superficie de un pedazo de papel. Este "cuadrado" se enfrenta a experimentos de un ser tridimensional. El ser tridimensional es percibido por el "cuadrado" como un ser aparentemente divino, ya que puede poner y quitar objetos de una caja fuerte sin romperla ni abrirla (moviéndolos a través de su tercera dimensión), ver todo desde de la perspectiva de dos dimensiones sea incluido detrás de las paredes (puesto que ve "sobre" Planilandia), y totalmente invisible para los habitantes de Planilandia, puesto que está "arriba" y una dimensión por arriba de las dos dimensiones en las que el cuadrado está atrapado. No obstante, el ser tridimensional podría manifestarse en el mundo de dos dimensiones, pero sólo parcialmente, si fuera una esfera, aparecería como una secuencia de círculos sucesivos "que cambian de tamaño" (intersecciones de la esfera con el plano de dos dimensiones). Aplicando analogía dimensional, uno puede deducir que el ser cuadridimensional sería capaz de hazañas similares de nuestra perspectiva tridimensional.
Rudy Rucker demuestra esto en su novela "Spaceland", en la cual el protagonista encuentra los seres cuadridimensionales que demuestran tales energías. Un uso útil de la analogía dimensional en visualizar la cuarta dimensión está en la proyección. Una proyección es una manera para representar un objeto (n+1)-dimensional en la n-dimensión. Por ejemplo, las pantallas de computadora son de dos dimensiones, y todas las fotografías de objetos tridimensionales son representadas en dos dimensiones puesto que la información de la tercera dimensión (o de la profundidad) no puede ser representada por la pantalla (si el observador se mueve, aleje o acerque, la imagen no cambiará). En este caso, la profundidad se quita y se substituye por la información indirecta. La retina del ojo es un arsenal de dos dimensiones de receptores pero puede permitir que el cerebro perciba la naturaleza de objetos tridimensionales usando la información indirecta (como la perspectiva, el sombreado, visión binocular, etc.).
La perspectiva del uso de los artistas da profundidad tridimensional a los cuadros de dos dimensiones. Asimismo, los objetos en la cuarta dimensión se pueden proyectar matemáticamente a las familiares tres dimensiones, donde pueden entonces ser examinados más convenientemente. En este caso, la "retina de un ojo cuadridimensional" tendría un arsenal de receptores tridimensionales. El ser hipotético con tal ojo percibiría la naturaleza de objetos cuadridimensionales usando la información indirecta contenida en las imágenes que recibe en su retina. La proyección de la perspectiva a partir de cuatro dimensiones produce efectos similares como en el caso tridimensional, tal como la perspectiva.
Esto agrega "profundidad cuadridimensional" a estos cuadros tridimensionales. La analogía dimensional también ayuda a entender tales proyecciones. Por ejemplo, los objetos de dos dimensiones son limitados por límites unidimensionales: un cuadrado es limitado por cuatro bordes o líneas. Los objetos tridimensionales son limitados por superficies de bidimensionales: un cubo es limitado por 6 cuadrados. Aplicando analogía dimensional, uno puede deducir que un cubo cuadridimensional, conocido como teseracto, es limitado por los volúmenes tridimensionales.
Y de hecho, éste es el caso matemáticamente: el teseracto es limitado por 8 cubos. Saber esto es indispensable para entender cómo interpretar una proyección tridimensional del teseracto. Los límites del teseracto proyectan a los volúmenes en la imagen, superficies no simplemente de dos dimensiones. Esto ayuda a entender las características de dichas dimensiones que de otra manera sólo confundirían. De igual manera, el concepto de sombras puede ayudarnos mejor a entender la teoría de cuatro dimensiones. Si usted proyectara una luz sobre objeto tridimensional, éste proyectaría una sombra de dos dimensiones. Por lo tanto la luz en un objeto de dos dimensiones echaría una sombra unidimensional (en un mundo de dos dimensiones), y la luz en un objeto unidimensional en un mundo unidimensional echaría una sombra cero-dimensional, es decir, un punto de la no-luz. Esta idea se puede utilizar en la otra dirección; la luz en un objeto cuadridimensional proyectaría una sombra tridimensional. Como ejemplo, la sombra de un cubo transparente, proyectaría una sombra sobre el papel, de dos cuadrados, unidos por sus vértices con 4 segmentos.
Semejantemente, si era un cubo cuadridimensional iluminado con luz de 4 dimensiones, su sombra sería la de un cubo tridimensional dentro de otro cubo tridimensional. Siendo tridimensionales podemos solamente ver el mundo con nuestros ojos en dos dimensiones; el ser cuadridimensional consideraría el mundo en tres. Así podría, por ejemplo, ver los seis lados de una caja opaca simultáneamente. No solamente eso; también podría ver lo que hay al interior de la caja, como en Planilandia, en donde la esfera ve objetos en el mundo de dos dimensiones y todo dentro de ellos simultáneamente. Análogo, un espectador cuadridimensional vería todos los puntos en nuestro espacio tridimensional simultáneamente, incluyendo la estructura interna de objetos sólidos y de cosas obscurecidos de nuestro punto de vista.
Albert Einstein en su célebre teoría de 1905 de la relatividad especial habló por primera vez del tiempo como una cuarta dimensión y como algo indispensable para ubicar un objeto en el espacio y en un momento determinado. El tiempo en la teoría de la relatividad no es una dimensión espacial más, ya que fijado un punto del espacio-tiempo éste puede ser no alcanzable desde nuestra posición actual, hecho que difiere de la concepción usual de dimensión espacial. Aunque inicialmente se interpretó el tiempo como una "dimensión" matemática necesaria para ubicar un evento u objeto, en la teoría de la relatividad general el tiempo es tratado como una dimensión geométrica más, aunque los objetos materiales no puedan seguir una trayectoria completamente arbitraria a lo largo del tiempo (como por ejemplo "dar la vuelta" y viajar al pasado). La necesidad del tiempo dentro de la teoría de la relatividad es necesaria por dos motivos:
En primer lugar, los objetos no sólo se mueven a través del espacio sino que también lo hacen a través del tiempo, es decir su coordenada temporal aumenta continuamente, por lo que hubo la necesidad de hablar del tiempo ligado al espacio como la cuarta dimensión (en inglés spacetime, en castellano espacio-tiempo). Además el ritmo de avance en la dimensión temporal depende del estado de movimiento del observador, produciéndose una dilatación temporal efectiva para los observadores más rápidos en relación al tiempo medido por un observador estacionario.
En segundo lugar, el carácter intrínseco del espacio-tiempo y su cuatridimensionalidad requiere un modo conceptualmente diferente de tratar la geometría del universo, puesto que una cuarta dimensión implica un espacio plano (bidimensional) que se curva en la teoría de la relatividad general por la acción de la gravedad de la materia originándose la curvatura del espacio-tiempo.
Finalmente cabe añadir que algunas teorías físicas como la teoría de Kaluza-Klein y las teoría de supercuerdas, en sus varias versiones, añaden a las tres dimensiones físicas espaciales entre 1 y 9 dimensiones espaciales adicionales, de tipo compacto; además de la dimensión temporal.
|
|
|
|
2 AL CUBO=8
3 AL CUBO=27
4 AL CUBO=64
5 AL CUBO=125
5 AL CUBO-CUATRO AL CUBO=5*5*5-4*4*4=125-64=61 (EXAGONAL)
4 AL CUBO-TRES AL CUBO=4*4*4-3*3*3=37 ("LLAVE DE DAVID")
3 AL CUBO-DOS AL CUBO=3*3*3-2*2*2=19 (EXAGONAL)
2 AL CUBO-UNO AL CUBO=2*2*2-1*1*1=7 (EXAGONAL)
LAS MATEMATICAS SON EXACTAS
APARENTEMENTE, EN ESTE CONTEXTO, LA PUERTA DE LA "CUARTA DIMENCION", EN EL CONTEXTO A LA RELACION DE QUE EL EXAGONO, TAMBIEN ES UN CUBO, EL OCTOGONO, SERIA LA PUERTA DEL HIPERCUBO, OSEA, INSISTO, LA CUARTA DIMENCION.
LAS MATEMATICAS SERIA:
2*2*2*2-1*1*1*1=15
CONSIDERANDO TAMBIEN AL CERO, ES UNA REFERENCIA AL 16, CODIFICADO EN EL MISMO VATICANO, EN EL PLANETA VENUS, EN EL SISTEMA DIGITAL, ETC,ETC.
|
|
|
|
|
|
|
|
Decimal --- Binario --- Cuaternario
00 -------- 0000 ------ 00
01 -------- 0001 ------ 01
02 -------- 0010 ------ 02
03 -------- 0011 ------ 03
04 -------- 0100 ------ 10
05 -------- 0101 ------ 11
06 -------- 0110 ------ 12
07 -------- 0111 ------ 13
08 -------- 1000 ------ 20
09 -------- 1001 ------ 21
10 -------- 1010 ------ 22
11 -------- 1011 ------ 23
12 -------- 1100 ------ 30
13 -------- 1101 ------ 31
14 -------- 1110 ------ 32
15 -------- 1111 ------ 33
9+6=15=1111 (BINARIO) = 33 (SISTEMA DE CUATRO NUMEROS)
0-1-2-3-4-5-6-7-8-9-10-11-12-13-14-15 (16 NUMEROS)
|
|
|
|
|
XLA X-stem Logic Alphabet and the New Jerusalem (tesseract)
note: the 16 CUBES
note: keep in mind that St. Peter Square, is demarcated by 16 'winds'
note: keep in mind that the Tarot KEY I have recovered (see below) clearly indicates we should notice the first 15 letters have passed, and currently the stem indicates MNO.
Which I have suggested can be rotated/reflected into words like OWN, NWO, ONE, WON, NOW, hey MON!
Thus the 16th letter on the TAROT KEY is P or p.
Now the p used in this next link/article will make so much more sense.
>>> http://www.logic-alphabet.net/mirrors_title.htm
Let The Mirrors Do The Thinking
and
Let The People Do The Reflecting
 
LANGUAGE, LETTER, NUMBER AND FORM COLLIDE
Be sure to link on the interview at the end of this post.
| Quote: |
Introduction
Our story begins with a simple example. Suppose that someone asked you to keep a record of your thoughts, exactly, and in terms of the symbols given, when you are making an effort to multiply XVI times LXIV. Also suppose that, refusing to give up, you finally arrive at the right answer, which happens to be MXXIV. We are sure that you would have had a much easier time of it, to solve this problem, if you would have found that 16 times 64 equals 1024.
This example not only looks at what we think and what we write. It also looks at the mental tools, the signs and symbols, that we are using when that thinking and that writing is taking place. How we got these mental tools is a long story, one that now includes the presence of some new developments.
Our main idea comes from calling attention to a deep commonality that cuts across the parallel streams of development that in recent millennia have unfolded in the ways and byways of evolutionary notation. It took many centuries of collective search to devise a place-value notation for counting. Likewise to devise a sound-value notation for reading. Likewise to devise a note-value notation for singing. And so forth, for each neurologically specialized ability; in effect, a different specialized notation for each specialized ability. These observations, easily recognized in the history of evolutionary notation, strongly suggest that every kind of intelligence needs its own kind of notation.
In what follows, with emphasis on a fast-forward recapitulation, we will run a replay of what happened when Europe took several centuries to go from MXXIV to 1024. This replay in not for numbers. It is for another specialized ability. It is for logic, when it is recast in terms of a shape-value notation. Modern logic starts in the middle of the 1800s and, as is well recognized, with the work of George Boole. This means that we have had only about 150 years to think up and to grow into the symbols we now use for symbolic logic.
These symbols, and they are only symbols, leave a lot to be desired. We hope that we can draw you into taking a look at a lesson in lazy logic. If you follow us all the way, we hope to leave you with a new set of signs, signs that are much better than any you have seen yet. Not only will it be much easier for you to use them. Even mirrors will be able to use them.
X-stem Logic Alphabet:
http://www.logic-alphabet.net/
Background:
http://www.logic-alphabet.net/background.htm |
Why only 15 cubes in this version of XLA?
It appears two have been combined into one.
Take a look at the first image of the tesseract.
It is clear in this second image the S and Z have been combined into one center cube.
And I find that interesting, because the S is one of the 8 vertices of the outside cube, and the Z belongs to one of the 8 vertices of the inner cube.
AHA??
Who does not see two intersecting SHAPES resembling 'SZ' in the center of the image above or in the image below we see a ZZ in the center of the 7000 year old plate found in Samarra Iraq....from the SZ, the SueZ region? 

What does the geometric shape look like if we reflect one of the 'Z' in ZZ into a S?
The SHAPE resembling an '8' perhaps?
More research is necessary in this fIELd by (me?) because the pieces are fitting rather well.
WOW MOM Interview with a kindred spirit:
http://www.cabinetmagazine.org/issues/18/crystal.php
I have found myself a new hero.
Shea Zellweger makes far more sense than that wanker Zechary Stitchen, in fact proving ZS along with his planet Nibiru are flights of UFO fancy taking off in his head and coming out of his mouth like a swarm of locusts.
May ZSitchen Rest In PieceS and some of his music decompose along with him.
YAhoo YAHU

Which reminds me of another TRUE to LIFE real hero who used his imagination NOT to script science fiction and confuse the sheeple even more like that wanker ZS, but instead the imagination of ELI-YAHU RIPS will still pay dividends to humanity in the years to come.
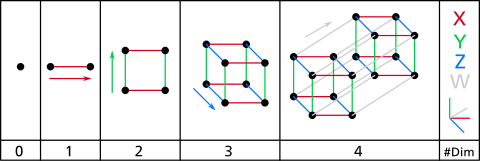
DOT >>> 1D LINE >>> 2D SQUARE >>> 3D CUBE >>> 4D TESSERACT
important to know about the tesseract:
http://en.wikipedia.org/wiki/Tesseract
| Quote: |

The tetrahedron forms the convex hull of the tesseract's vertex-centered central projection. Four of 8 cubic cells are shown. The 16th vertex is projected to infinity and the four edges to it are not shown.
http://en.wikipedia.org/wiki/Tesseract
|
namaste
_________________
KEY 528=Swastika=ancient Spherical Standing Wave Theory
“A theory is more impressive the greater is the simplicity of its premise, the more different are the kinds of things it relates and the more extended its range of applicability…”
-Albert Einstein |
|
|
|
|
| Quote: |
| I am acquainted, for instance , with an Egyptian ceremonial system, some 5,000 years old, which taught precisely the same things as Masonry does, but in the terms of shipbuilding instead of in the terms of architecture. |
How much sense does that make?
Too much.
First we are given dimensions for Noah to build an ARK and then later we are given dimensions with which to build Solomon's Temple, that which contains an 'Ark of the Covenant'.
And the New Jerusalem to come is just over the hori-zion. 
The importance of the numbers 3 and 7 to a Freemason.
| Quote: |
3
To each of us also from our birth have been given three lesser lights, by which the Lodge within ourselves may be illumined. For the " sun " symbolizes our spiritual consciousness, the higher aspirations and emotions of the soul; the " moon " betokens our reasoning or intellectual faculties, which (as the moon reflects the light of the sun) should reflect the light coming from the higher spiritual faculty and transmit it into our daily conduct; whilst " the Master of the Lodge " is a symbolical phrase denoting the will-power of man, which should enable him to be master of his own life, to control his own actions and keep down the impulses of his lower nature, even as the stroke of the Master's gavel controls the Lodge and calls to order and obedience the Brethren under his direction.
|

69
Please note the coincidences re Sun and Moon:
The 6x6 magic square of the Sun is connected to the number 666.
(i.e. 666 = the sum of the numbers 1-36 used to comprise the 6x6 square)
The 9x9 magic square of the Moon is connected to daily Sudoko playing and Tesla's 369.
| Quote: |
7
Brethren, I charge you to regard your apron as one of the most precious and speaking symbols our Order has to give you. Remember that when you first wore it was a piece of pure white lambskin; an emblem of that purity and innocence which we always associate with the lamb and with the new-born child. Remember that you first wore it with the flap raised, it being thus a five-cornered badge, indicating the five senses, by means of which we enter into relations with the material world around us (our "five points of fellowship " with the material world), but indicating also by the triangular portion above, in conjunction with the quadrangular portion below, that man's nature is a combination of soul and body; the three-sided emblem at the top added to the four-sided emblem beneath making seven, the perfect number; for, as it is written in an ancient Hebrew doctrine with which Masonry is closely allied, "God blessed and loved the number seven more than all things under His throne," by which is meant that man, the seven-fold being, is of the most cherished of all the Creator's works. And hence also it is that the Lodge has seven principal officers, and that a Lodge, to be perfect, requires the presence of seven brethren; though the deeper meaning of this phrase is that the individual man, in virtue of his seven-fold constitution, in himself constitutes the " perfect Lodge," if he will but know himself and analyse his own nature aright.
http://www.masonicsecrets.org/meaning-of-masonry/deeper-symbolism-of-freemasonry.html |
Interesting to note that in the bI6LE, in the Book of Revelations, the number 7 appears 137 times.
good site 
namaste
_________________
KEY 528=Swastika=ancient Spherical Standing Wave Theory
“A theory is more impressive the greater is the simplicity of its premise, the more different are the kinds of things it relates and the more extended its range of applicability…”
-Albert Einstein
http://breakfornews.com/forum/viewtopic.php?t=6522&postdays=0&postorder=asc&start=180&sid=8a7cd78184dee77cf1a2d112d2054c49
|
|
|
|
|
Them boyz is cooking over on the 2012 forums.
| Quote: |
God's Numbers = 137 (english)
137 = The Golden Mean
-->1.618 "The Golden Mean"
-->1.618 minutes = 1:37 (min/sec)
137 = The Messiah Yeshua/God
-->13.7 minutes = 822 seconds
-->8/22 (AUG 22) = 234th Day
Yeshua's Numbers = 190 (english)
-->19.0 minutes = 1140 seconds
-->11:40 PM = 23:40
The Number of the Messiah = 234.0 (english)
-->8:22 PM = 20:22
-->The Value of the Messiah = 222.0 (english)
-->2:22 is opposite 10:38 on a clock face
-->1038 seconds = 17.3 minutes
-->Yehoshua HaMashiach = 173 (english)
173rd Day (JUN 22) = 193 Days Remain/leap year
-->193 seconds = 3:13 (min/sec)
-->Yehoshua HaMashiach = 313 (reverse) 173 (english)
173rd Day (JUN 22) = 192 Days Remain
-->The Numbers of the Most High God = 1092 (jewish)
-->www.gematrix.org (jewish gematria calculator)
-->Yehoshua's Number = 1209 (jewish)
6/22 =173rd/174th Day
--->(the day of 'IMMINENT THREAT/WORLD TRADE CENTER ATTACK')
--->FAA Circular (keyword search)
The Number of the Messiah = 234 (english) 333 (reverse eng.)
1,7/4 = 2,3/4
1,7/3 = 3.33
173rd/174th Day = 6/22
622 seconds = 10:22 (min/sec)
10:22 PM = 22:22
Isaiah 22:22 "THE KEY"
Why 222, 22:22?
2:00 forms a Hexagon Star (Star of David/60 degrees)
-Lord Jesus Christ = 200 (english)
-200 seconds = 3.33 minutes
1/333 = 0.0300300
3:00 (min/hr hand at 12/3)
Lord Jesus Christ = 205 (english)
20.5 minutes = 1230 seconds
The Number Three Hundred Thirty-Three = 1904 (jewish gematria)
19:04 = 7:04 PM
Yeshua = 704 (jewish)
Jesus = 74.0 (english)
Who is the Most High God? = 1533 (jewish)
15:33 = 3:33 PM
hr/min/sec hand at 3/3/3 (3:15:15)
PM? = 15:15:15
15 = 5+2+8
Yehoshua = 528 (Hebrew)
152 (RE:137)
God's Numbers = 152 (reverse english)
152nd Day = 6/1
-->God = 61 (jewish)
min/hr hand at 6/1 (6/05)
6/05 = 156th Day
Yeshua = 156 / God = 156
-->156 seconds = 2.6 minutes
-->God = 26 (english)
What is Yeshua's Number? = 251 (english)
-->25.1 minutes = 1506 seconds
The Golden Mean (as follows)
1 + sq.root of 5 divided by 2
216 days remain = 150th Day (5/30 -leap year)
5:30 PM = 17:30
Yehoshua HaMashiach = 173.0 (english) 313 (reverse english)
1,7/3 = 3.33
3.33 (written as 3,1/3 -three and one third)
@ 11 Aquarius. 3 Gemini, 7 Libra
11:37 PM = 23:37
23.7 minutes = 1422 seconds
14:22 = 2:22 PM
2:22 is opposite 10:38 on a clock face
1038 seconds = 17.3 (minutes)
Yehsohua HaMashiach = 173 (english)
The Value of the Messiah = 222 (english) |
http://2012forum.com/forum/viewtopic.php?f=60&t=26341
_________________
TRIA SUNT MIRABILIA DEUS ET HOMO MATER ET VIRGO TRINUS ET UNUS |
|
|
 Primer Primer
 Anterior
56 a 70 de 190
Siguiente Anterior
56 a 70 de 190
Siguiente Último
Último
|

