De Wikipedia, la enciclopedia libre
La divergencia de un campo vectorial mide la diferencia entre el flujo saliente y el flujo entrante de un campo vectorial sobre la superficie que rodea a un volumen de control, por tanto, si el campo tiene "fuentes" la divergencia será positiva y "sumideros" la divergencia será negativa.
Divergencia de un campo vectorial [editar]
La divergencia de un campo vectorial en un punto es un campo escalar, y se define como el flujo del campo vectorial por unidad de volumen conforme el volumen alrededor del punto tiende a cero:
donde 
es una superficie cerrada que se reduce a un punto en el límite. El símbolo 
representa el operador nabla.
Esta definición está directamente relacionada con el concepto de flujo del campo. Como en el caso del flujo, si la divergencia en un punto es positiva, se dice que el campo posee fuentes. Si la divergencia es negativa, se dice que tienesumideros. El ejemplo más característico lo dan las cargas eléctricas, que dan la divergencia del campo eléctrico, siendo las cargas positivas manantiales y las negativas sumideros del campo eléctrico.
Se llaman fuentes escalares del campo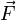 
al campo escalar que se obtiene a partir de la divergencia de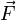
La divergencia de un campo vectorial se relaciona con el flujo a través del teorema de Gauss o teorema de la divergencia.
Coordenadas cartesianas [editar]
Cuando la definición de divergencia se aplica al caso de un campo expresado en coordenadas cartesianas,
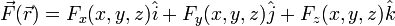
el resultado es sencillo:
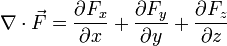
Coordenadas ortogonales [editar]
Sin embargo, para un caso más general de coordenadas ortogonales curvilíneas, como las cilíndricas o las esféricas, la expresión se complica debido a la dependencia de los vectores de la base con la posición. La expresión para un sistema de coordenadas ortogonales es:
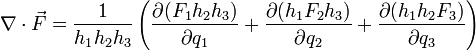
Donde los 
son los factores de escala del sistema de coordenadas, relacionados con la forma del tensor métrico en dicho sistema de coordenadas. Esta fórmula general, para el caso de coordenadas cartesianas (
) se reduce a la expresión anterior.
Para coordenadas cilíndricas (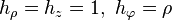
) resulta:
Para coordenadas esféricas (
) resulta
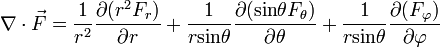
Coordenadas generales [editar]
En sistemas de coordenadas generales, no necesariamente ortogonales, la divergencia de un vector puede expresarse en términos de las derivadas parciales respecto a las coordenadas y el determinante del tensor métrico:
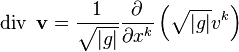
Divergencia de un campo tensorial [editar]
El concepto de divergencia puede extenderse a un campo tensorial de orden superior. En una variedad de Riemann la divergencia de un tensor T completamente simétrico
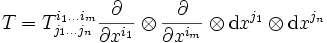
Se define como:
![[operatorname{div} T]_{j_1dots j_n}^{i_1 dots i_m} = abla_{alpha}T_{j_1 dots j_n}^{i_1 dots i_{m-1} alpha} = part_alpha T_{j_1,dots,j_n}^{i_1 dots i_{m-1}alpha} + Gamma^{i_1}_{alphaeta}T_{j_1 dots,j_n}^{eta dots i_m}+ dots + Gamma^{i_m}_{alphaeta}T_{j_1 dots,j_n}^{i_1 dots eta}](http://upload.wikimedia.org/math/d/a/2/da28ae5d38f209af3939c3ad3369d74e.png)
Por ejemplo, en teoría de la relatividad especial la energía de un sistema se representa por un tensor simétrico de segundo orden, cuya divergencia es cero. De hecho el principio de conservación de la energía relativista toma la forma:
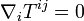
Teorema de la divergencia [editar]
El teorema de la divergencia, frecuentemente llamado teorema de Gauss, relaciona el flujo de un campo vectorial a través de una superficie cerrada con la integral de la divergencia de dicho campo en el interior del volumen encerrado por una superficie. Ese resultado lo hace interesante en aplicaciones relacionadas con la electrostática como en la mecánica de fluidos.
El teorema se enuncia así: Sea una función vectorial 
diferenciable definida sobre un conjunto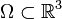 
y sea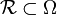 
un conjunto cerrado limitado por una frontera 
o superficie de contorno (que sea una variedad diferenciable) y sea 
el vector normal en cada punto de la superficie, entonces se cumple que:
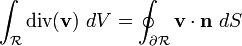
Véase también [editar]
http://es.wikipedia.org/wiki/Divergencia_(matem%C3%A1ticas)
Tema anterior
