|
|
General: QUE ES EL SISTEMA? MATRIX
Escolher outro painel de mensagens |
|
|
| De: tertulo (Mensagem original) |
Enviado: 23/03/2012 06:22 |
|
|
 Primeira
Primeira
 Anterior
2 a 15 de 15
Seguinte
Anterior
2 a 15 de 15
Seguinte
 Última
Última

|
|
|
EVERYTHING IS CONNECTED AND THERE ARE NO COINCIDENCES |
|
|
|
|

es.walyou.com
2 Alcancia cubo Rubik
521 × 423 - 24k - jpg |

es.wikipedia.org
El interior de un cubo de
232 × 199 - 28k - jpg |

solostocks.com
Cubo Mágico
500 × 500 - 29k - jpg |

pocoseso.com
del Rubik - Cubo Magico -
450 × 338 - 28k - jpg |
Búsquedas relacionadas con cubo magico
EL MISMO "CUBO MAGICO" ES UN HIPERCUBO (HAY UN CUBO MAS CHICO EN EL CENTRO DEL MISMO)
| Reply |
Message 24 of 24 on the subject |
|
El término cuarta dimensión aparece en diversos contextos como la física, las matemáticas y la ciencia ficción. En cada contexto el significado es diferente:
En física, se hace referencia a la cuarta dimensión al hablar del tiempo, principalmente desde el planteamiento de la Teoría de la Relatividad.
En matemática, el concepto aparece asociado o bien a espacios euclídeos de más de tres dimensiones o, más generalmente, a espacios localmente euclídeos o 4-variedades diferenciables.

Hipercubo de 4 dimensiones espaciales girando, tal como se vería proyectado en el espacio tridimensional.
El interés en las dimensiones más altas alcanzó su clímax entre 1870 y 1920.1 En esos años se convirtió en tema frecuente en la literatura fantástica, el arte e incluso algunas teorías científicas. La cuarta dimensión, entendida como dimensión espacial adicional (no como dimensión temporal, como en la teoría de la relatividad) apareció en las obras literarias de Oscar Wilde, Fiódor Dostoyevski, Marcel Proust, H. G. Wells y Joseph Conrad, inspiró algunas obras musicales de Alexander Scriabin, Edgar Varèse y George Antheil y algunas obras plásticas de Pablo Picasso y Marcel Duchamp influyendo en el desarrollo del cubismo. Incluso personajes tan diversos como el psicólogo William James, la escritora Gertrude Stein o el socialista revolucionario Vladimir Lenin se interesaron en el tema.
Igualmente los matemáticos habían estado interesados en el tema al tratar de generalizar los conceptos de la geometría euclídea tridimensional. El matemático Charles L. Dodgson, que enseñó en la Universidad de Oxford, deleitó a generaciones de escolares escribiendo libros, bajo el pseudónimo de Lewis Carroll, que incorporaban algunas ideas sobre la cuarta dimensión. Desde el punto de vista académico, el estudio general de la geometría de la cuarta dimensión en gran parte resultado de los trabajos de Bernhard Riemann. Charles Howard Hinton, matemático y escritor de ciencia ficción británico, acuñó muchos neologismos para describir elementos en la cuarta dimensión. De acuerdo con el Oxford English Dictionary, fue el primero en emplear la palabra tesseract en su libro Una nueva era del pensamiento. También inventó las palabras “kata” (del griego “abajo”) y “ana” (del griego “arriba”) para describir las dos direcciones opuestas en la cuarta dimensión, equivalentes a derecha-izquierda, arriba-abajo, y adelante-atrás.
Los trabajos matemáticos sobre geometrías multidimensionales y geometrías no euclídeas habían sido considerado por los físicos como simples abstracciones matemáticas hasta que Henri Poincaré probó que el grupo de transformaciones de Lorentz que dejaban invariantes las ecuaciones del electromagnetismo podían ser interpretadas como "rotaciones" en un espacio de cuatro dimensiones. Más tarde, los trabajos de Einstein y la interpretación geométrica de estos por parte de Hermann Minkowski llevaron a la aceptación de la cuarta dimensión como una descripción necesaria para explicar los hechos observados relacionados con el electromagnetismo. Sin embargo, aquí la "cuarta dimensión" no era un lugar separado del espacio tridimensional (como en varias de las obras de ficción de la época) ni tampoco una dimensión espacial análoga a las otras tres dimensiones espaciales, sino una dimensión temporal que sólo puede recorrerse hacia el futuro. En la teoría general de la relatividad el campo gravitatorio es explicado como un efecto geométrico de la curvatura de un espacio-tiempo de cuatro dimensiones.
Más tarde, la teoría de Kaluza-Klein propuso que no sólo el campo gravitatorio podía ser interpretado de forma más sencilla como curvatura de un "espacio" de más de tres dimensiones, sino que si se introducía una nueva dimensión espacial enrollada o «compactificada», también el campo electromagnético podía ser interpretado como un efecto geométrico de la curvatura de dimensiones superiores. Así, la Kaluza proponía una teoría de campo unificado del electromagnetismo y la gravedad en un espacio-tiempo de cinco dimensiones, con una dimensión temporal, tres dimensiones espaciales extendidas y una dimensión espacial «compactificada» adicional, que, debido a su condición de compactificada, no era directamente visible pero su efecto era perceptible en forma de campo electromagnético.

Un ángulo recto se describe como un cuarto de una revolución. La Geometría Cartesiana escoge direcciones ortogonales arbitrariamente a través del espacio, lo que significa que cada dirección está en ángulo recto con las demás. Las 3 dimensiones ortogonales del espacio se conocen como altitud, longitud y latitud. La Cuarta Dimensión por lo tanto es la dirección en el espacio con ángulo recto a las 3 direcciones observables.
Un vector espacial es un conjunto de vectores, los cuales podemos imaginarlos como flechas, que proviene de un simple lugar llamado origen (vectores geométricos), que apuntan a otros lugares.
Un punto es un objeto de cero dimensiones. No tiene extensión en el espacio ni propiedades, como una flecha pero sin longitud. Este vector es llamado el vector cero y es el más simple vector espacial.
Una línea es un objeto unidimensional. Si escogemos un cierto vector distinto a cero en una cierta dirección, este vector tiene cierta longitud definida. Ese vector tiene una cabeza en un cierto punto en espacio y una cola en el origen. Si pensamos en estirar que ese vector así sea dos veces su largo, tres veces, etcétera y uniformemente, tomando todas las longitudes posibles (incluso la longitud cero, conseguir el vector cero), conseguiremos una sola línea con una sola dimensión: La de la longitud. Todos los vectores que describen puntos en esta línea serían paralelos. Aunque para visualizar la línea es necesario que ésta tenga un ancho mínimo, sin embargo, una línea de 1D no la tendría.
Un plano es un objeto de dos dimensiones. Tiene longitud y anchura pero no profundidad - algo como una hoja de papel, o más exactamente algo como las imágenes en un televisor común. El pensamiento en un plano en términos de vectores puede ser un poco más desafiante. Si pensamos en tomar un vector y lo movemos de modo que su cola esté tocando la cabeza del primero y esté formando un vector con su cola en el origen y la cabeza en la cabeza del segundo vector colocado de nuevo, tenemos una manera razonable de hablar de vectores de adición. Si tenemos dos vectores que no sean paralelos, podemos hablar de todos los puntos que podemos alcanzar por o solamente el estirar o ningunos de los vectores, y, agregando estos vectores juntos, estos puntos forman un plano.
El espacio, como lo percibimos, es tridimensional. Podemos pensar en poner una línea junto con un plano. Estas líneas son como un emparedado. Para conseguir a un cierto punto en espacio, podemos imaginarnos el viajar encima de la línea y después el movernos a través del plano al punto. Entonces tenemos tres vectores a pensar alrededor, uno a viajar una cierta distancia encima de la línea y dos para conseguir a un cierto punto en espacio.
Para tres rectas ortogonales en el espacio tridimensional (x, y y z) existe una cuarta, normal al espacio, ortogonal a estas tres rectas, que forma un eje p. ej. w.
El producto vectorial es la determinante de una matriz 4×4, donde una de las filas (o columnas) son los vectores unitarios h, i, j y k y las demás (filas o columnas respectivamente) están formadas por las componentes de tres vectores cuadradimensionales cualesquiera, este producto nos dará un cuarto vector perpendicular a estos tres mismos.
La Geometría euclidiana prevé una mayor variedad de formas para existir que en tres dimensiones. Los poliedros tridimensionales son recintos espaciales hechos de caras de dos dimensiones conectadas, los policronos cuadridimensionales son recintos del espacio cuadridimensional hechos de poliedros tridimensionales. Donde en tres dimensiones, hay exactamente cinco poliedros regulares, o los sólidos platónicos, que pueden existir, seis policronos regulares existen en la cuarta dimensión. Cinco de los seis se pueden interpretar como extensiones naturales de los sólidos platónicos, así como el cubo, un sólido platónico, es una extensión del cuadrado de dos dimensiones. El pentachoron está hecho de 5 tetraedros para las caras y 10 caras triangulares, y es el análogo cuadridimensional del tetraedro. El teseracto, o el hipercubo, se compone de 8 caras cúbicas y de 24 cuadrados, y es el politopo cuadridimensional medido. Los teseractos se doblan, la 16-celdas, son el equivalente del octaedro, pues son ambos politopos de cruz. Los politopos de 120 celdas y los de 600 celdas se doblan de igual modo, y son análogos al dodecaedro y al icosaedro, respectivamente. El de 24 celdas es un policrono regular único y que no tiene ningún equivalente tridimensional. Apenas pues la esfera, o 2-esfera, es una superficie de dos dimensiones curvada compuesta de todos los puntos equidistantes de un punto central dado, en un espacio tridimensional, la 3-esfera, una clase de hiperesfera, es el espacio que contiene todos los puntos equidistantes a un punto central dado, en un espacio cuadridimensional. Cada sección transversal tridimensional de un 3-esfera es un 2-esfera.

La analogía dimensional se usa frecuentemente para comprender el salto de una dimensión (en este caso, la tercera dimensión) a una más alta (cuarta dimensión). La analogía dimensional consiste en resolver un problema en n + 1 dimensiones relacionándolo primero con un problema análogo de (n - 1) dimensión, vale decir, "una dimensión menos". E igualmente debe analizarse el caso de cómo se relaciona el problema en n con el de (n + 1) dimensiones, es decir, "una más".
Edwin Abbott Abbott en su libro Planilandia (Flatland) escribe sobre un "ser cuadrado" que vive en un mundo de dos dimensiones, como la superficie de un pedazo de papel. Este "cuadrado" se enfrenta a experimentos de un ser tridimensional. El ser tridimensional es percibido por el "cuadrado" como un ser aparentemente divino, ya que puede poner y quitar objetos de una caja fuerte sin romperla ni abrirla (moviéndolos a través de su tercera dimensión), ver todo desde de la perspectiva de dos dimensiones sea incluido detrás de las paredes (puesto que ve "sobre" Planilandia), y totalmente invisible para los habitantes de Planilandia, puesto que está "arriba" y una dimensión por arriba de las dos dimensiones en las que el cuadrado está atrapado. No obstante, el ser tridimensional podría manifestarse en el mundo de dos dimensiones, pero sólo parcialmente, si fuera una esfera, aparecería como una secuencia de círculos sucesivos "que cambian de tamaño" (intersecciones de la esfera con el plano de dos dimensiones). Aplicando analogía dimensional, uno puede deducir que el ser cuadridimensional sería capaz de hazañas similares de nuestra perspectiva tridimensional.
Rudy Rucker demuestra esto en su novela "Spaceland", en la cual el protagonista encuentra los seres cuadridimensionales que demuestran tales energías. Un uso útil de la analogía dimensional en visualizar la cuarta dimensión está en la proyección. Una proyección es una manera para representar un objeto (n+1)-dimensional en la n-dimensión. Por ejemplo, las pantallas de computadora son de dos dimensiones, y todas las fotografías de objetos tridimensionales son representadas en dos dimensiones puesto que la información de la tercera dimensión (o de la profundidad) no puede ser representada por la pantalla (si el observador se mueve, aleje o acerque, la imagen no cambiará). En este caso, la profundidad se quita y se substituye por la información indirecta. La retina del ojo es un arsenal de dos dimensiones de receptores pero puede permitir que el cerebro perciba la naturaleza de objetos tridimensionales usando la información indirecta (como la perspectiva, el sombreado, visión binocular, etc.).
La perspectiva del uso de los artistas da profundidad tridimensional a los cuadros de dos dimensiones. Asimismo, los objetos en la cuarta dimensión se pueden proyectar matemáticamente a las familiares tres dimensiones, donde pueden entonces ser examinados más convenientemente. En este caso, la "retina de un ojo cuadridimensional" tendría un arsenal de receptores tridimensionales. El ser hipotético con tal ojo percibiría la naturaleza de objetos cuadridimensionales usando la información indirecta contenida en las imágenes que recibe en su retina. La proyección de la perspectiva a partir de cuatro dimensiones produce efectos similares como en el caso tridimensional, tal como la perspectiva.
Esto agrega "profundidad cuadridimensional" a estos cuadros tridimensionales. La analogía dimensional también ayuda a entender tales proyecciones. Por ejemplo, los objetos de dos dimensiones son limitados por límites unidimensionales: un cuadrado es limitado por cuatro bordes o líneas. Los objetos tridimensionales son limitados por superficies de bidimensionales: un cubo es limitado por 6 cuadrados. Aplicando analogía dimensional, uno puede deducir que un cubo cuadridimensional, conocido como teseracto, es limitado por los volúmenes tridimensionales.
Y de hecho, éste es el caso matemáticamente: el teseracto es limitado por 8 cubos. Saber esto es indispensable para entender cómo interpretar una proyección tridimensional del teseracto. Los límites del teseracto proyectan a los volúmenes en la imagen, superficies no simplemente de dos dimensiones. Esto ayuda a entender las características de dichas dimensiones que de otra manera sólo confundirían. De igual manera, el concepto de sombras puede ayudarnos mejor a entender la teoría de cuatro dimensiones. Si usted proyectara una luz sobre objeto tridimensional, éste proyectaría una sombra de dos dimensiones. Por lo tanto la luz en un objeto de dos dimensiones echaría una sombra unidimensional (en un mundo de dos dimensiones), y la luz en un objeto unidimensional en un mundo unidimensional echaría una sombra cero-dimensional, es decir, un punto de la no-luz. Esta idea se puede utilizar en la otra dirección; la luz en un objeto cuadridimensional proyectaría una sombra tridimensional. Como ejemplo, la sombra de un cubo transparente, proyectaría una sombra sobre el papel, de dos cuadrados, unidos por sus vértices con 4 segmentos.
Semejantemente, si era un cubo cuadridimensional iluminado con luz de 4 dimensiones, su sombra sería la de un cubo tridimensional dentro de otro cubo tridimensional. Siendo tridimensionales podemos solamente ver el mundo con nuestros ojos en dos dimensiones; el ser cuadridimensional consideraría el mundo en tres. Así podría, por ejemplo, ver los seis lados de una caja opaca simultáneamente. No solamente eso; también podría ver lo que hay al interior de la caja, como en Planilandia, en donde la esfera ve objetos en el mundo de dos dimensiones y todo dentro de ellos simultáneamente. Análogo, un espectador cuadridimensional vería todos los puntos en nuestro espacio tridimensional simultáneamente, incluyendo la estructura interna de objetos sólidos y de cosas obscurecidos de nuestro punto de vista.
Albert Einstein en su célebre teoría de 1905 de la relatividad especial habló por primera vez del tiempo como una cuarta dimensión y como algo indispensable para ubicar un objeto en el espacio y en un momento determinado. El tiempo en la teoría de la relatividad no es una dimensión espacial más, ya que fijado un punto del espacio-tiempo éste puede ser no alcanzable desde nuestra posición actual, hecho que difiere de la concepción usual de dimensión espacial. Aunque inicialmente se interpretó el tiempo como una "dimensión" matemática necesaria para ubicar un evento u objeto, en la teoría de la relatividad general el tiempo es tratado como una dimensión geométrica más, aunque los objetos materiales no puedan seguir una trayectoria completamente arbitraria a lo largo del tiempo (como por ejemplo "dar la vuelta" y viajar al pasado). La necesidad del tiempo dentro de la teoría de la relatividad es necesaria por dos motivos:
En primer lugar, los objetos no sólo se mueven a través del espacio sino que también lo hacen a través del tiempo, es decir su coordenada temporal aumenta continuamente, por lo que hubo la necesidad de hablar del tiempo ligado al espacio como la cuarta dimensión (en inglés spacetime, en castellano espacio-tiempo). Además el ritmo de avance en la dimensión temporal depende del estado de movimiento del observador, produciéndose una dilatación temporal efectiva para los observadores más rápidos en relación al tiempo medido por un observador estacionario.
En segundo lugar, el carácter intrínseco del espacio-tiempo y su cuatridimensionalidad requiere un modo conceptualmente diferente de tratar la geometría del universo, puesto que una cuarta dimensión implica un espacio plano (bidimensional) que se curva en la teoría de la relatividad general por la acción de la gravedad de la materia originándose la curvatura del espacio-tiempo.
Finalmente cabe añadir que algunas teorías físicas como la teoría de Kaluza-Klein y las teoría de supercuerdas, en sus varias versiones, añaden a las tres dimensiones físicas espaciales entre 1 y 9 dimensiones espaciales adicionales, de tipo compacto; además de la dimensión temporal.
|
|
|
|
2 AL CUBO=8
3 AL CUBO=27
4 AL CUBO=64
5 AL CUBO=125
5 AL CUBO-CUATRO AL CUBO=5*5*5-4*4*4=125-64=61 (EXAGONAL)
4 AL CUBO-TRES AL CUBO= 4*4*4-3*3*3= 37 ("LLAVE DE DAVID")
3 AL CUBO-DOS AL CUBO=3*3*3-2*2*2=19 (EXAGONAL)
2 AL CUBO-UNO AL CUBO=2*2*2-1*1*1=7 (EXAGONAL)
LAS MATEMATICAS SON EXACTAS
APARENTEMENTE, EN ESTE CONTEXTO, LA PUERTA DE LA "CUARTA DIMENCION", EN EL CONTEXTO A LA RELACION DE QUE EL EXAGONO, TAMBIEN ES UN CUBO, EL OCTOGONO, SERIA LA PUERTA DEL HIPERCUBO, OSEA, INSISTO, LA CUARTA DIMENCION.
LAS MATEMATICAS SERIA:
2*2*2*2-1*1*1*1=15
CONSIDERANDO TAMBIEN AL CERO, ES UNA REFERENCIA AL 16, CODIFICADO EN EL MISMO VATICANO, EN EL PLANETA VENUS, EN EL SISTEMA DIGITAL, ETC,ETC.
|
|
|
|
|
|
|
The Great Pyramid and the Speed of Light
The Great Pyramid encodes enormous amount of numerical coincidences ( pi, Phi, dimensions and movement of our planet, axial tilt, precession, speed of light, and more…)
We can only wonder if the ancient architects were fully aware of these special numbers encoded in their design — or are these numbers simply the result of selecting 2 numbers (7 and 11) for proportions for the Great Pyramid???
|
|
The design of the Great Pyramid is based on the ratio 11:7. This ratio (equal 1.571) is perfect approximation of the “squaring the circle” principle.

For the Great Pyramid, Base to Height Ratio 440/280 is exactly 11/7
Most “pyramidologists” appear to be “chasing their tails” uncovering huge amount of “numerical coincidences” embedded in the Great Pyramid…
It is simply unbelievable, however ALL of these numerical coincidences are result of selecting just 4 numbers for the pyramid design: 7, 11 (height to base ratio), 40 (the scale factor), and the 4th key number is the value of the measuring unit: Royal Cubit = 20.62 ” = 0.524 m.
|
This single, fundamental design principle: 11 : 7 Base to Height Ratio generates ALL amazing mathematical properties of the Great Pyramid:
- the Golden Ratio Phi=1.618 (the Great Pyramid is a Golden Pyramid: length of the slope side (356) divided by half of the side (440/2 = 220) height is equal to 1.6181818… which is the Golden Ratio Phi
- squaring the circle ratio 1.571 (base/height = 44/28 = 1.571)
- pi=3.14159… (2 x base/height = 2 x 44/28 = 3.14286 which is very close approximation of “pi” = 3.14159…)
- Perimeter of the square base, 4×440=1760, is the same as circumference of the circle with radius = height: 2x ”pi” x height (2x 22/7 x 280=1760)
- The ratio of the perimeter to height of 1760/280 cubits equates to 2x pi
to an accuracy of better than 0.05%
- Side of the base (440) plus double height (2x 280=560) = 1,000
- Perimeter of the square base is equal 4×440=1760 RC = 0.5 nautical mile = 1/7,200th of the radius length of the earth
- the slop angle 51°.843
- The Pyramid exhibits in the design both pi and by Phi, given the similarity
of 2/ sqrt(phi) (2 divided by the square root of Phi) with pi/2 :
- 11/ 7 equal 1.5714
- 2/ sqrt(89/55) equal 1.5722
- 2/ sqrt(Phi) equal 1.5723
- pi/ 2 equal 1.5708
- Royal Cubit = 0.5236 m, pi – Phi2 = 0.5231
- and more…
Does Great Pyramid encode “fractal” value of the speed of light?
The speed of light in a vacuum is 299, 792, 458 meters per second or 983,571,056.43045 feet per second or 186,282.397 miles per second.
Base of the Great Pyramid is a square with side B = 44o Royal Egyptian Cubits. Let’s draw two circles: one inscribed and one superscribed on the square of the base of the Great Pyramid.

- Circumference of superscribed circle: 2x pi x R
- Circumference of the inscribed circle: 2x pi x r
The difference of the circumference of both circles (lets call it C) is:
C = 2 x pi x (R – r) = 2 x pi x [ B/sqrt(2) - B/2 ] =
2x pi x B x [ 1/sqrt(2) - 1/2 ] = 1.301290285 x B
The length of the Egyptian Royal Cubit
Based on “The Pyramids and Temples of Gizeh” by W.M. Flinders Petrie. 1883.
The unit of measuring length used by the ancient architects in the construction of the Great Pyramid was the Royal Cubit.
Petrie estimated the value of the Royal Cubit using some key dimensions of the Great Pyramid:
By the base length of the Pyramid, if 440 cubits (section ’43): 20.611 ± .002
By the base of King’s Chamber, corrected for opening of joints: 20.632 ± .004 inches
By the Queen’s Chamber, if dimensions squared are in square cubits: 20.61 ± .020
By the antechamber: 20.58 ± .020
By the ascending and Queen’s Chamber passage lengths (section 149): 20.622 ± .002
By the gallery width: 20.605 ± .032
The Average value of the RC (based on above numbers) is 20.61 inches.
It’s almost universally accepted that archaeologist Flinders Petrie’s determination of the royal cubit length at 20.632 inches, from his measurements of the King’s Chamber in the Great Pyramid of Giza, was the likely measure to survey the dimensions of that pyramid, 440 royal cubits per base side, but the experts stop there, not then letting you know that those 1,760 royal cubits which total the Great Pyramid’s base perimeter length, when multiplied by 20.632 inches, equals half a modern nautical mile, or 1/7,200th of the radius length of the earth, so there certainly is a connection.
EL EXAGONO Y LA RELACION CON EL PI=22/7-LAS MATEMATICAS CONFIRMAN LA RELACION EXAGONAL CON MARIA LA MAGDALENA EN EL MISMO DIA DE SU DIA EN LA IGLESIA CATOLICA, OSEA EL 22 DE JULIO (22/7)
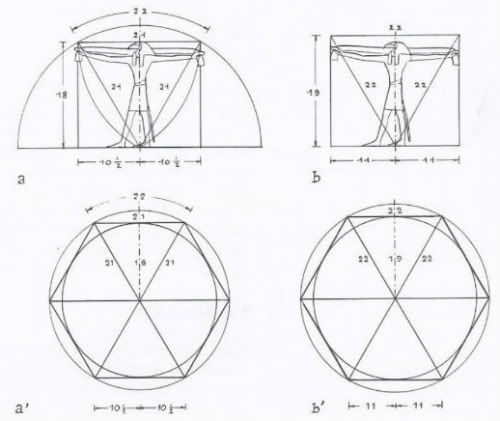 Temple of Man Schwaller de Lubicz page 177 Serpents in the Sky by John Anthony West Temple of Man Schwaller de Lubicz page 177 Serpents in the Sky by John Anthony West
Noten que tenemos el SECTOR CIRCULAR, en un contexto matematico exagonal, la relacion matematica 22/11. Sabemos que la longitud de la circunferencia es igual al numero PI=3.14=22/7 por el DIAMETRO=RADIO*2 del circulo. En un contexto a que tenemos segun la figura superior la LONGITUD DE ARCO (PI/3-RADIANES) que es igual a 22 si hacemos las matematicas:
LONG. CIRC.=3.14*DIAMETRO=3.14*2*RADIO=22/7*2*21=22/7*2*7*3=(22*2*7*3)/7=22*6
LONG. CIRC.=22*6=132=33*4 (IMPRESIONANTE RELACION DEL NUMERO 33)
Noten que estamos haciendo referencia al exagono y es obvia su interrelacion con el planeta Mercurio, que insisto, esta interrelacionada con la ESTRELLA DE DAVID, OSEA EL HIJO DEL MISMO DAVID, QUE FUE EL REY SOL-O-MON. El 33, insisto, es una referencia a los dos triangulos, de la estrella de 6 puntas. Ahora, si la longitud del arco es igual a PI/3 (RADIANES) tenemos la relacion:
22/21=22/(7*3)=(22/7)/3=PI/3
IMPRESIONANTE DE QUE BELLAS SON LAS MATEMATICAS.
LA MISMA PALABRA REVOLU-SION ES UNA REFERENCIA AL NUMERO PI (LONGITUD DE LA CIRCUNFERENCIA ES IGUAL A PI X DIAMETRO.)
|
| Reply |
Message 61 of 61 on the subject |
|
|
|
|
|
|
|
|
AD UNIVERSI VIRTUALIS ORBIS SUMMI ARCHITECTI GLORIAM

|
|
|
|
|
Noten la fuerte relacion del MUNDIAL CON EL LINAJE. COMIENZAN 32 EQUIPOS, CLASIFICAN 16, LUEGO SIGUEN 8, LUEGO 4, LUEGO 2 Y EL CAMPEON MUNDIAL ES EL GRIAL MISMO.
MASONERIA PURA.
LA COPA ES EL GRIAL MISMO, OSEA LA SANTA CENA
NO HAY PEOR NARCISISTA QUE EL QUE VIENDO NO QUIERE CREER.
ES OBVIA LA CONNOTACION MASONICA CON EL LINAJE O EL ARBOL GENEALOGICO. UN HIJO TIENE DOS PADRES, CUATRO ABUELOS, 8 BISABUELOS, 16 TATARAABUELOS OSEA UNA REFERENCIA A 2 ELEVADO A LA N en el marco a que N=1,2,3,4,5,6,7,......,INFINITO. N ES OBVIAMENTE TIENE REFERENCIA AL NUMERO DE GENERACION. EL ARBOL, OBVIAMENTE, ES LA MISMA MANZANA.
MUNDO MISOGINO, QUE NO QUIERE CREER QUE CRISTO TUVO UN MUJER.
LA MUJER TIENE QUE HACERSE CARGO, DE QUE LA RELIGION SEA MACHISTA Y MISOGINA.
EL MISMO ARBOL GENEALOGICO
|
|
|
|
|
| e: Rolmen |
Enviado: 27/07/2018 18:18 |
|
11. que decía: Yo soy el Alfa y la Omega, el primero y el último. Escribe en un libro lo que ves, y envíalo a las siete iglesias que están en Asia: aEfeso, Esmirna, Pérgamo, Tiatira, Sardis, Filadelfia y Laodicea. (UNA CLARA REFERENCIA A LAS PLEYADES, OSEA A LA CONSTELACION DEL TORO / TAURO)
|

888+888=1776
TORRE DE LA LIBERTAD=1776 PIES
OBVIO QUE EL NORTEAMERICANO MIRA BIEN EL ESPEJO
¿EL CRISTIANO CREE EN EL ESPEJO?
OBVIO, QUE NO POR SU NARCISISMO
|
|
|
|
|
|
|
22/7=3.14=PI
12 PUNTOS EN SU CIRCUNFERENCIA=RELOJ=SANTA CENA
LONGITUD CIRCUNFERENCIA=PIxDIAMETRO
 |
|
|
|
|
|
|
|
|
|
|

GRAN DRAGÓN ESCARLATA O BESTIA DE 7 CABEZAS:
ISLA SAN GIORGIO (VENECIA)=GEORGE LEMAITRE
Sapientia Aedificavit Sibi Domum. Es decir, "la sabiduría ha edificado aquí su casa". Resulta curioso que la misma frase aparece en el Evangelio de María Magdalena, un texto apócrifo. Se dice que en el interior de esta iglesia y de otras muchas de Venecia está escondido el tesoro de los templarios. Pero no hay ninguna prueba de ello. Para terminar ya con esta entrada me gustaría que nos acercásemos un momento a uno de los edificios más emblemáticos de Venecia: el Palacio Ducal.

La Maddalena

Tomb of Tommaso Temanza
|
|
|
 Primeira
Primeira
 Anterior
2 a 15 de 15
Seguinte
Anterior
2 a 15 de 15
Seguinte
 Última
Última

|
|
| |
|
|
©2025 - Gabitos - Todos os direitos reservados | |
|
|

