Hace tiempo que me fascinan los fenómenos de phi (letra griega), la serie de números de Fibonacci y la proporción divina, la proporción áurea , la media áurea, la proporción áurea, la espiral áurea , el rectángulo áureo . Para mí, esta es una evidencia tan clara de la existencia de Dios y de su gran genio en la creación de todas las cosas en la naturaleza. Si nunca has oído hablar de esto, míralo, ¡te sorprenderás! Pero aquí hay algunos hechos y ejemplos para que comiences.
Hace tiempo que me fascinan los fenómenos de phi (letra griega), la serie de números de Fibonacci y la proporción divina, la proporción áurea , la media áurea, la proporción áurea, la espiral áurea , el rectángulo áureo . Para mí, esta es una evidencia tan clara de la existencia de Dios y de su gran genio en la creación de todas las cosas en la naturaleza. Si nunca has oído hablar de esto, míralo, ¡te sorprenderás! Pero aquí hay algunos hechos y ejemplos para que comiences.
 En matemáticas, la serie de Fibonacci son los números en la siguiente secuencia de números enteros:
En matemáticas, la serie de Fibonacci son los números en la siguiente secuencia de números enteros:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc. donde los primeros dos números son 0 y 1, y cada número subsiguiente = la suma de los 2 números anteriores.
Y Phi = 1,6180339887 ... o la relación de cualquier número de Fibonacci con el número anterior en la secuencia, por ejemplo, 8/5, 13/8, etc.

Espiral Dorada
La serie de Fibonacci lleva el nombre de Leonardo de Pisa , quien introdujo la secuencia en las matemáticas de Europa occidental, aunque la secuencia se había descrito anteriormente en las matemáticas indias. Los números de Fibonacci se utilizan en el análisis de los mercados financieros. También aparecen en entornos biológicos, como la ramificación de los árboles, la disposición de las hojas en un tallo , los brotes de la fruta de una piña , la floración de una alcachofa , un helecho que se despliega y la disposición de una piña.
Puedes ver esta divina proporción de belleza en todos los aspectos de la creación, desde la botánica hasta la zoología, el cuerpo humano, el rostro humano en particular, en el espectro de colores, en las escalas y acordes musicales, en la astronomía, en la arquitectura, incluso en la patrones de nuestro ADN! y especialmente para este puesto, en las instrucciones de Dios a los judíos en la construcción de artículos tales como el Arca santa de la Alianza, el Arca de Noé , los arreglos de colores en el Tabernáculo Judío en Éxodo. Evidentemente, Dios diseñó el universo con esta proporción como base de su apariencia, desde el microcosmos hasta el macrocosmos. Estos son solo algunos ejemplos de este fenómeno.
 Una concha marina Nautilis es uno de los ejemplos más exquisitos de la proporción divina.
Una concha marina Nautilis es uno de los ejemplos más exquisitos de la proporción divina.
Algunas plantas tienen hermosos patrones repetitivos en espiral en sus estructuras que incorporan el llamado ángulo dorado (aproximadamente 137,5 grados). Los aficionados a las matemáticas, los artistas y los místicos apreciarán que el ángulo dorado está relacionado con la "proporción divina" que aparece con frecuencia en formas estéticamente agradables.
 Las plantas con patrones en espiral relacionados con el ángulo áureo también muestran otra curiosa propiedad matemática. Las semillas de una cabeza de flor forman espirales entrelazadas en sentido horario y antihorario. El número de espirales en el sentido de las agujas del reloj difiere del número de espirales en el sentido contrario a las agujas del reloj, y estos dos números se denominan números parastiquios de la planta (pronunciados pi-RAS-tik-ee o PEHR-us-tik-ee). Estos números tienen una consistencia notable. Casi siempre son dos números de Fibonacci consecutivos .
Las plantas con patrones en espiral relacionados con el ángulo áureo también muestran otra curiosa propiedad matemática. Las semillas de una cabeza de flor forman espirales entrelazadas en sentido horario y antihorario. El número de espirales en el sentido de las agujas del reloj difiere del número de espirales en el sentido contrario a las agujas del reloj, y estos dos números se denominan números parastiquios de la planta (pronunciados pi-RAS-tik-ee o PEHR-us-tik-ee). Estos números tienen una consistencia notable. Casi siempre son dos números de Fibonacci consecutivos .
Phi en la Biblia y la Creación
Aunque tal vez no sea inmediatamente obvio, phi y la proporción áurea aparecen en la Biblia.
El Arca de la Alianza es un Rectángulo Dorado
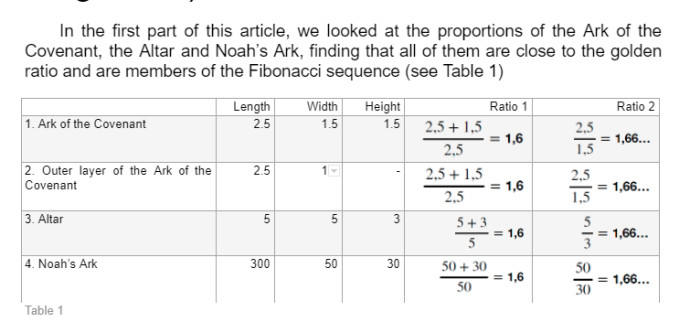
En Éxodo 25:10, Dios le ordena a Moisés que construya el Arca del Pacto , en la cual celebrar Su Pacto con los israelitas, los Diez Mandamientos, diciendo: “Que hagan un cofre de madera de acacia, de dos codos y medio de largo, codo y medio de ancho, y codo y medio de alto. La proporción de 2,5 a 1,5 es 1,666 ..., que es lo más cercano a phi (1,618...) que se puede obtener con números tan simples y ciertamente no es visiblemente diferente a la vista. El Arca de la Alianza se construye así utilizando la Sección Áurea, o Proporción Divina. Esta proporción también es la misma que 5 a 3, números de la serie de Fibonacci.
En Éxodo 27:1-2, encontramos que el altar que Dios le ordena a Moisés que construya está basado en una variación del mismo tema de 5 por 3: “Edifica un altar de madera de acacia, de tres codos de altura; será cuadrado, de cinco codos de largo y cinco codos de ancho.
Nota: Un codo es la medida del antebrazo debajo del codo.
El Arca de Noé usa un Rectángulo Dorado
En Génesis 6:15, Dios le ordena a Noé que construya un arca diciendo: “Y de esta manera la harás: la longitud del arca será de trescientos codos, su anchura de cincuenta codos, y la altura de treinta codos. Así, el extremo del arca, de 50 por 30 codos, también está en una proporción de 5 a 3, o 1.666..., nuevamente una aproximación cercana de phi no visiblemente diferente a simple vista. El arca de Noé fue construida en la misma proporción que diez arcas del pacto colocadas una al lado de la otra.
Los colores del Tabernáculo se basan en una relación phi
Como dice en Éxodo 26:1, “Haz el tabernáculo con diez cortinas de lino fino torcido y de hilo azul, púrpura y escarlata, con querubines labrados por un hábil artífice”. Esta referencia a la combinación de azul, púrpura y escarlata en la construcción del tabernáculo aparece 24 veces en Éxodo 25 al 39, describiendo los colores que se usarán en las cortinas, cinturones, pectorales, fajas y vestiduras.
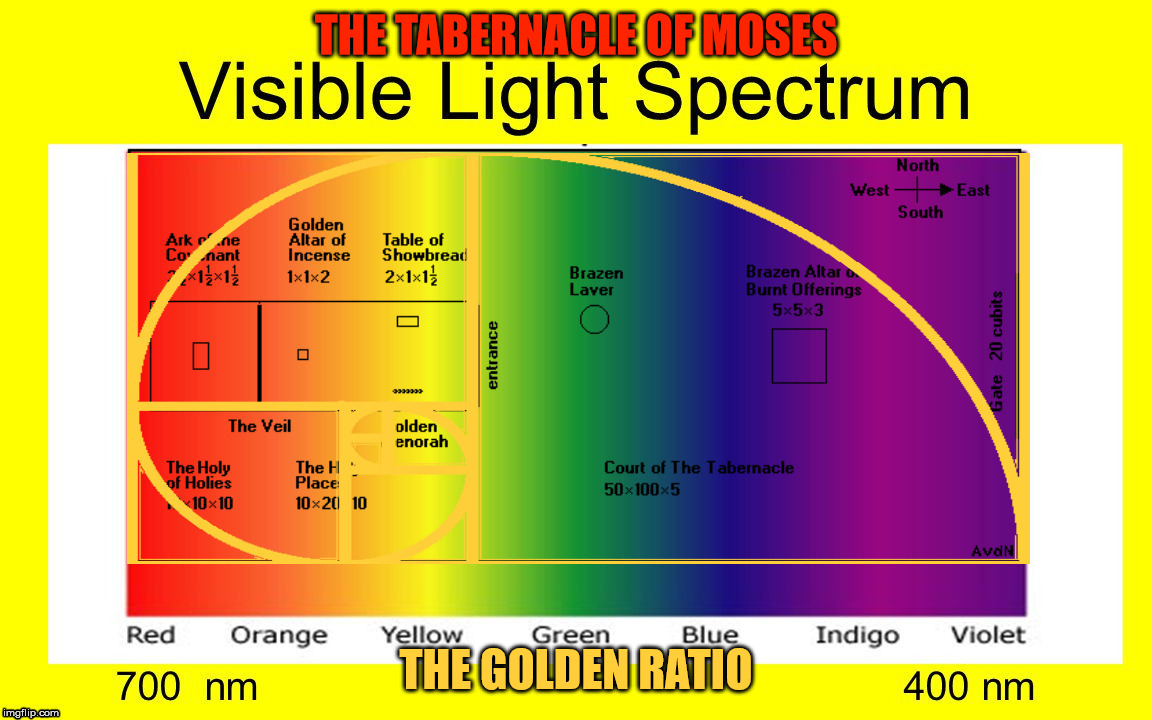
Las relaciones Phi en un espectro de colores producen combinaciones de colores ricas y atractivas
Michael Semprevivo ha introducido un concepto llamado PhiBar, que aplica relaciones phi a frecuencias, o longitudes de onda, en el espectro de colores visibles en la luz. Los colores del espectro que están relacionados por distancias basadas en phi o la sección áurea producen combinaciones muy ricas y visualmente atractivas. Esto se ilustra a continuación en la captura de pantalla de su programa PhiBar. Puede experimentar con el programa PhiBar, escrito en Visual Basic, haciendo clic AQUÍ para descargarlo y luego ejecutar el archivo .exe.
 Nota: Michael Semprevivo pone a disposición este programa de forma gratuita solo para uso no comercial. El programa PhiBar.exe se escaneó con el programa antivirus de Norton el 01/03/2003 utilizando las definiciones de virus actuales y se encontró que está libre de virus, pero no se otorgan garantías expresas o implícitas con respecto a su uso.
Nota: Michael Semprevivo pone a disposición este programa de forma gratuita solo para uso no comercial. El programa PhiBar.exe se escaneó con el programa antivirus de Norton el 01/03/2003 utilizando las definiciones de virus actuales y se encontró que está libre de virus, pero no se otorgan garantías expresas o implícitas con respecto a su uso.
El PhiBar produce las combinaciones de colores del Tabernáculo como se describe en la Biblia
Usando el programa PhiBar anterior, JD Ahmanson descubrió que produce los colores que la Biblia dice que Dios le dio a Moisés para la construcción del Tabernáculo.
La espiral del ADN es una Sección Dorada
La molécula de ADN, el programa para toda la vida, se basa en la sección áurea. Mide 34 angstroms de largo por 21 angstroms de ancho por cada ciclo completo de su espiral de doble hélice. 34 y 21, por supuesto, son números en la serie de Fibonacci y su proporción, 1,6190476, se aproxima mucho a phi, 1,6180339.
Las escalas musicales se basan en los números de Fibonacci
 La serie de Fibonacci aparece en la base de aspectos del arte, la belleza y la vida. Incluso la música tiene una base en la serie, como:
La serie de Fibonacci aparece en la base de aspectos del arte, la belleza y la vida. Incluso la música tiene una base en la serie, como:
Hay 13 notas en el lapso de cualquier nota a través de su octava. Una escala se compone de 8 notas, de las cuales la 5.ª y la 3.ª crean la base básica de todos los acordes, y se basan en un tono completo que está a 2 pasos del tono fundamental, que es la 1.ª nota de la escala.
Tenga en cuenta también cómo la escala del teclado de piano de C a C arriba de 13 teclas tiene 8 teclas blancas y 5 teclas negras, divididas en grupos de 3 y 2. Mientras que algunos podrían "observar" que solo hay 12 "notas" en la escala, si no tiene una raíz y una octava, un comienzo y un final, no tiene forma de calcular las gradaciones intermedias, por lo que esta nota 13 como octava es esencial para calcular las frecuencias de las otras notas. La palabra “octava” proviene de la palabra latina para 8, refiriéndose a los ocho tonos enteros de la escala musical completa, que en la tonalidad de C son CDEFGABC.
En una escala, la nota dominante es la nota 5 de la escala mayor, que también es la nota 8 de las 13 notas que componen la octava. Esto proporciona una instancia adicional de números de Fibonacci en relaciones musicales clave. Además, la típica canción de tres acordes en la tonalidad de A se compone de A, su pareja de Fibonacci & phi E, y D, con la que A guarda la misma relación que E con A. Esto es análogo a “A is a B como B es a C” base de la sección áurea, o en este caso “D es a A como A es a E”.
Los instrumentos musicales a menudo se basan en phi.
Los números de Fibonacci y phi se utilizan en el diseño de violines e incluso en el diseño de cables de altavoces de alta calidad.

¿Has visto suficiente? ¿No es Dios asombroso en su ingeniería precisa y hermosa? ¡Y pensar que algunos todavía creen que todo sucedió por casualidad! Podría seguir, ¡pero este post se está haciendo largo! ¡Míralo tú mismo y sorpréndete más! Mucha de esta información está tomada de este sitio web: http://goldennumber.net/index.htm .