
The azimuth is the angle formed between a
reference direction (in this example north) and a
line from the observer to a point of interest projected on the same plane as the reference direction orthogonal to the
zenith.
An azimuth (; from Arabic: اَلسُّمُوت, romanized: as-sumūt, lit. 'the directions')[1] is the horizontal angle from a cardinal direction, most commonly north, in a local or observer-centric spherical coordinate system.
Mathematically, the relative position vector from an observer (origin) to a point of interest is projected perpendicularly onto a reference plane (the horizontal plane); the angle between the projected vector and a reference vector on the reference plane is called the azimuth.
When used as a celestial coordinate, the azimuth is the horizontal direction of a star or other astronomical object in the sky. The star is the point of interest, the reference plane is the local area (e.g. a circular area with a 5 km radius at sea level) around an observer on Earth's surface, and the reference vector points to true north. The azimuth is the angle between the north vector and the star's vector on the horizontal plane.[2]
Azimuth is usually measured in degrees (°), in the positive range 0° to 360° or in the signed range -180° to +180°. The concept is used in navigation, astronomy, engineering, mapping, mining, and ballistics.
The word azimuth is used in all European languages today. It originates from medieval Arabic السموت (al-sumūt, pronounced as-sumūt), meaning "the directions" (plural of Arabic السمت al-samt = "the direction"). The Arabic word entered late medieval Latin in an astronomy context and in particular in the use of the Arabic version of the astrolabe astronomy instrument. Its first recorded use in English is in the 1390s in Geoffrey Chaucer's Treatise on the Astrolabe. The first known record in any Western language is in Spanish in the 1270s in an astronomy book that was largely derived from Arabic sources, the Libros del saber de astronomía commissioned by King Alfonso X of Castile.[3]
In the horizontal coordinate system, used in celestial navigation, azimuth is one of the two coordinates.[4] The other is altitude, sometimes called elevation above the horizon. It is also used for satellite dish installation (see also: sat finder). In modern astronomy azimuth is nearly always measured from the north.

Azimuth marker, Mount Allen (
Sandstone Peak), southern California, US
In land navigation, azimuth is usually denoted alpha, α, and defined as a horizontal angle measured clockwise from a north base line or meridian.[5][6] Azimuth has also been more generally defined as a horizontal angle measured clockwise from any fixed reference plane or easily established base direction line.[7][8][9]
Today, the reference plane for an azimuth is typically true north, measured as a 0° azimuth, though other angular units (grad, mil) can be used. Moving clockwise on a 360 degree circle, east has azimuth 90°, south 180°, and west 270°. There are exceptions: some navigation systems use south as the reference vector. Any direction can be the reference vector, as long as it is clearly defined.
Quite commonly, azimuths or compass bearings are stated in a system in which either north or south can be the zero, and the angle may be measured clockwise or anticlockwise from the zero. For example, a bearing might be described as "(from) south, (turn) thirty degrees (toward the) east" (the words in brackets are usually omitted), abbreviated "S30°E", which is the bearing 30 degrees in the eastward direction from south, i.e. the bearing 150 degrees clockwise from north. The reference direction, stated first, is always north or south, and the turning direction, stated last, is east or west. The directions are chosen so that the angle, stated between them, is positive, between zero and 90 degrees. If the bearing happens to be exactly in the direction of one of the cardinal points, a different notation, e.g. "due east", is used instead.
True north-based azimuths
[edit]
From north, eastern side
| Direction | Azimuth |
| N |
0° |
| NNE |
22.5° |
| NE |
45° |
| ENE |
67.5° |
| E |
90° |
| ESE |
112.5° |
| SE |
135° |
| SSE |
157.5° |
From north, western side
| Direction | Azimuth |
| S |
180° |
| SSW |
202.5° |
| SW |
225° |
| WSW |
247.5° |
| W |
270° |
| WNW |
292.5° |
| NW |
315° |
| NNW |
337.5° |
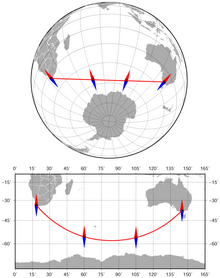
The azimuth between
Cape Town and
Melbourne along the
geodesic (the shortest route) changes from 141° to 42°.
Azimuthal orthographic projection and
Miller cylindrical projection.
We are standing at latitude �1 , longitude zero; we want to find the azimuth from our viewpoint to Point 2 at latitude �2
, longitude zero; we want to find the azimuth from our viewpoint to Point 2 at latitude �2 , longitude L (positive eastward). We can get a fair approximation by assuming the Earth is a sphere, in which case the azimuth α is given by
, longitude L (positive eastward). We can get a fair approximation by assuming the Earth is a sphere, in which case the azimuth α is given by
- tan�=sin�cos�1tan�2−sin�1cos�

A better approximation assumes the Earth is a slightly-squashed sphere (an oblate spheroid); azimuth then has at least two very slightly different meanings. Normal-section azimuth is the angle measured at our viewpoint by a theodolite whose axis is perpendicular to the surface of the spheroid; geodetic azimuth (or geodesic azimuth) is the angle between north and the ellipsoidal geodesic (the shortest path on the surface of the spheroid from our viewpoint to Point 2). The difference is usually negligible: less than 0.03 arc second for distances less than 100 km.[10]
Normal-section azimuth can be calculated as follows:[citation needed]
- �2=�(2−�)1−�2=(1−�)2Λ=(1−�2)tan�2tan�1+�21+(1−�2)(tan�2)21+(1−�2)(tan�1)2tan�=sin�(Λ−cos�)sin�1

where f is the flattening and e the eccentricity for the chosen spheroid (e.g., 1⁄ 298.257223563 for WGS84). If φ1 = 0 then
- tan�=sin�(1−�2)tan�2

To calculate the azimuth of the Sun or a star given its declination and hour angle at a specific location, modify the formula for a spherical Earth. Replace φ2 with declination and longitude difference with hour angle, and change the sign (since the hour angle is positive westward instead of east).[citation needed]

