|
|
General: NUMERO 44=RESURRECCION DE LAZARO=44 HS VATICANO=HIPERCUBO=GESTACION BEBE
Escolher outro painel de mensagens |
|
|
|
| Reply |
Message 11 of 24 on the subject |
|
|
| Reply |
Message 224 of 224 on the subject |
|
TUESDAY, MAY 18, 2010
BORROMEAN RINGS (1/3)
“If one proceeded to announce that there is still nowadays a work of the former Egyptians, one of their books that escaped the flames that devoured their superb libraries, and which contains their purest doctrines on interesting subjects, everyone who heard, undoubtedly, would hasten to study such an invaluable book, such a marvel. If one also said that this book is very widespread in most of Europe, that for a number of centuries it has been in the hands of everyone, the surprise would be certain to increase. Would it not reach its height, if one gave assurances that no one ever suspected that it was Egyptian; that those who possessed it did not value it, that nobody ever sought to decipher a sheet of it; that the fruit of an exquisite wisdom is regarded as a cluster of extravagant figures which do not mean anything by themselves? Would it not be thought that the speaker wanted to amuse himself, and played on the credulity of his listeners?”
BORROMEAN RINGS
RING ONE: hidden element
3 Rings linked together, their centers being vertices (corners) of an equilateral Triangle.
Viewed in this diagram, we are looking at a 2-dimensional map of Earth from its side, represented by One ring of our choosing (blue): 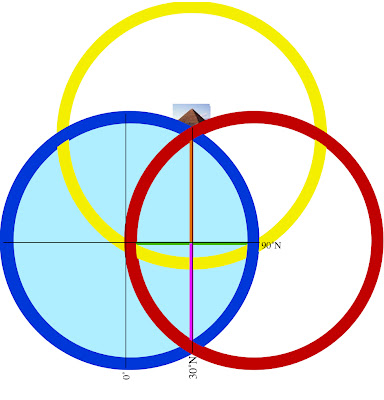 Orient the planet so the Great Pyramid at Giza (30˚N) lays at one of the vertices, the Earth’s center at another, and its axis’ North pole at the third. Exploring this set of relations, it can be demonstrated that the architectural proportions of the Great Pyramid at Giza exhibit a means of utilizing the measure of Earth to express the mathematical constant, π. To understand how we must suspend, for a moment, our habit of thinking of number in purely quantitative terms and consider the ways in which some numbers are also inherently bound to specific geometric forms - like with ‘square’ (1² 2² 3² 4² 5²...) or ‘cubed’ (1³ 2³ 3³ 4³ 5³...) numbers we see a sum attached to a particular shape. Other shapes each possess their own sequence of numbers also attached to their change in proportion. These are called ‘figurate numbers’, and tradition has it they were introduced into Greek mathematics by the pre-Socratic philosopher, Pythagoras, in the 6th century BC. A student of the ancient mystery schools, it is likely he acquired this knowledge during his journeys to Chaldea & Egypt; but all that is really required to calculate the number sequences tied to these shapes is a stack of pebbles and time to spare, counting out the variety of polygons & devising ways of stacking them to construct polyhedrons. To the careful interpreter of nature a pattern was discernible amidst this numerical data - One that, properly placed, could be applied to the measure of all things. It is suggested here that the Great Pyramid at Giza, in relation to the 3-Ring structure given above, embodies this application. Let us then imagine the Great Pyramid as keystone to a system of ‘projective numerology’ - an application of mathematics using figurate numbers to model distances and proportions as shapes, and translating them into their related forms as ‘seen’ from different angles & in other dimensions. At the root of any square pyramid’s architecture is its’ seked - an ancient Egyptian ratio of angular measure used to determine the slope of a pyramid’s sides and thus its’ height.  Utilizing the seked of the Great Pyramid, the perimeter of a square pyramidal base equals the circumference of a circle whose radius is equal to that pyramid’s height. Within our 2-dimensional map, as our planet rotates upon its’ axis, the Pyramid appears to move from one end of a vesica piscis to the other, as if turning on a Wheel whose rim is the 30th parallel. Thus, in one quarter turn (11/14 ≈ π/4) the Pyramid appears to move in a perpendicular line to the base of the equilateral Triangle articulated within our 3-ring diagram. 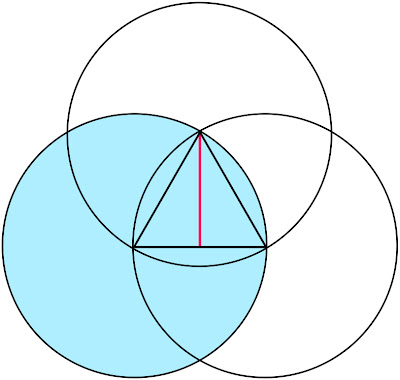  The distance of this perpendicular line from the Great Pyramid to the Earth’s polar axis is 3430 nautical miles, or 10x the cube of seven. Let us then imagine this distance as a stack of 10 cubes, 7x7x7.  A ‘quarter turn’ (11/14) of the Earth thus ‘apportions’ a 10x10 square of these cubes: 10² x 14/11 = 127.27272727...  So, by the logic induced with this arrangement of proportions, distances can be pictured in the mind’s Eye as figurate numbers of octahedral symmetry with 7-unit sides. Reading the Run & Rise of the Great Pyramid’s seked both forward and backward we get a formula for modeling a linear distance of the Earth’s measure as a column made of figurative cubes. 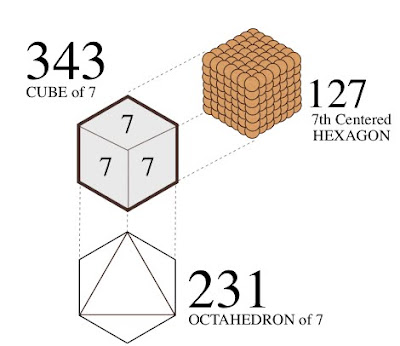 [3d:2d = 343 : 127 ] [3d:2d = 343 : 127 ]As such, we can picture the square pyramid monument atop this ‘column’ as pointing to the center of an imaginary 11th cube. 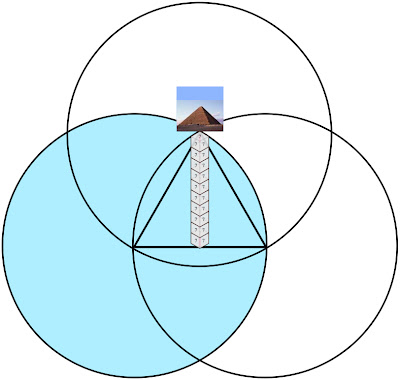 It follows, then, that a 12-hour rotation (180˚) measures a distance from center-point to center-point of the cubes at either end of a column 22 cubes of 7 long. 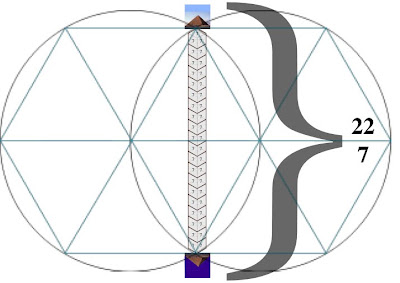 The center point of a unit cube has a specific relationship to the vesica piscis traversed in this 12-hour ‘distance’ within our diagram, as Two rings sharing a single radius give a rational approximation for √3, which is also the space diagonal of any unit cube. 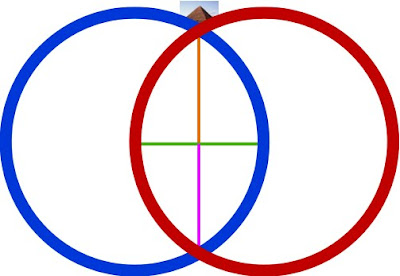 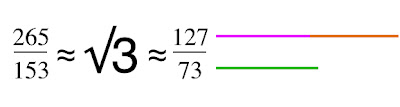 In other words, with respect to a unit cube, the √3 is the distance between opposite corners of that cube. Tracing these space diagonal lines joins the opposing corners, all of which intersect at the center of that cube, and thereby delineate the edges of six square pyramids joined at their apex. 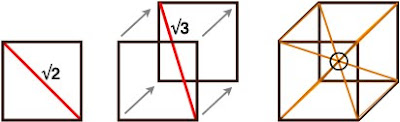 22:7 ≈ π 22:7 ≈ πTo the Egyptian god Thoth, equated with the Greek god, Hermes, and particularly the Roman god, Mercury, this ratio is significant in describing the number of conjunctions aligning Mercury & Earth with the Sun every 7 years. Also known as a ‘synodic cycle’, this is an example of what ancient Greek astronomers called an exeligmos, or ‘Turn of the Wheel’ - describing any period wherein Sun, Moon, and/or planets return to conjunction(s) from which they started. The term is still used today, but is more specifically applied to the Triple Saros cycle of reckoning lunar eclipses, each 120º of longitude apart, eventually returning to a point relatively close to where they began: exeligmos. The Romans used the term annus magnus, or ‘great year’ to describe the same class of periodic event. As we shall see, each of the planets have a harmonic ratio of conjunctions with our planet Earth, and with each other. By fixing the Earth to the center of our ecliptic plane, the motion of other planets relative to our position appear as serpentine spiro-graph patterns, looping in close when aligning into conjunction with the Sun, and looping out to trace a wide arc that coils about the Earth until looping in again for another conjunction. 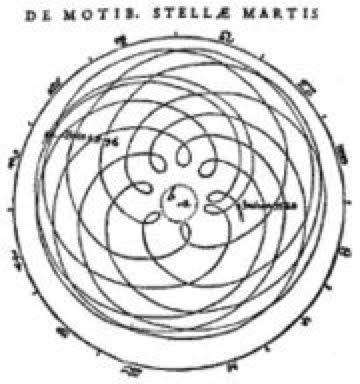 Mars:Earth  Venus: Earth Consistent within our model of 10 cubes of seven, the Great Pyramid (pointing to the center of an eleventh) also corresponds to the tip of an octahedron of 7 = 231. And it just so happens that 11x 231 is the number of days in the exeligmos of Mercury & Earth, 22:7. In addition, the measure of the Great Pyramid’s base side lengths (440 cubits each) give a total base area measuring approximately 231 meters square. Being a close approximation of the value π, and our annus magnus with the planet Mercury (Hermes/Thoth), let us then imagine this column of 22 cubes of 7 as the staff of his Caduceus. As we shall see, the cycles of the other planets can be represented as the serpents entwined about this Staff, their helices in tune with the ratio of their exeligmos. Imparting more than just the inevitable passage of Time, they were the very music of the spheres by which the harmony of creation was made known to the ancient Geometers. Our 3-Rings establish the base unit of an entire system of weights & measures (metrology) by symbolizing an angular dimension constructed by the movement through Time of the Great Pyramid, like the point of a metronome entrained to the Earth’s tempo. In effect attuning the mathematical constant π with Mercury's Great Year & the linear measure of Earth's size in units of angular measure. 'Squaring' the circle much like the Great Pyramid's seked. 1 nautical mile = 1.15 miles The nautical mile used as our base unit of measure for obtaining the distance in cubes of seven is also a unit of angular measure equivalent to 1/60th degree of Earth longitude (=1 minute of arc degree). Converting this into survey land miles = 1/10² the number of days between Earth:Mercury conjunctions (=115).  22:7 = 12 hrs @ 30˚north (12x 30 = 360) 180˚ = 10,800 arc minutes of degree = 50x 216, the cube of 6 216 also equals the number of degrees between Earth:Venus conjunctions (x5 = 1 Earth:Venus pentagram = exeligmos). So, by subdividing each degree of arc into 60 minutes, Earth’s 180˚ rotation (22:7) upon its’ axis thereby possesses a kind of numerological resonance regarding its harmonic with Venus, the exeligmos of the pentagram. Reputedly a symbol of good will among the Pythagoreans, the pentagram also provides an easy means of obtaining the golden ratio. 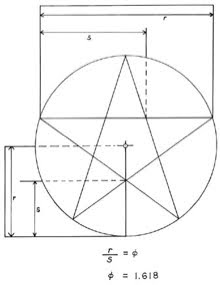  12 : 1 = (22/7) = 60 minutes In this way our measure of both Time & Space define each other by weaving together the value π with the ‘divine proportion’ of the golden ratio. Of the numerous other curious facets to this TooL of Hermetic Metrology, establishing not only our system of weights & measures, its choice of cubes & octahedrons also exhibit a direct connection to speeds of both sound & light: 1 meter =distance trave1ed by sound 1/343th of second =distance trave1ed by light 1/299,792,458th of second 343 = cube of 7 299,792,458 = c = speed of light in meters per second 1296000 / π = number of square degrees in one whole sphere c / 1296000 = 231.321.... 231 = octahedron of 7 Stranger still, the proportions outlined above are also paralleled in the numerical structure of the Tarot de Marseilles’ pattern of 22 major arcana trumps when applied to the Hebrew alphabet - in turn derived from Egyptian (via proto-Sinaitic) hieroglyphs which depicted the symbols those letters are still associated with. 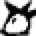 We see traces of this tradition within our own English alphabet with the letter A: also the glyph for an Ox head (turned upside-down) having the same origin as the Hebrew letter aleph.  Referred to by 'occultists' as the Book of Thoth (though never adequately explained why), the key to unlocking this puzzle, as with any cryptological TooL, is knowing where to place the cypher, or sifr - the arabic word from which we also get Zero, or ‘nothing’, the rank of every Tarot deck’s Fool [aleph=0]. And this role proves more than suitable for One who ushers in what ultimately reveals a prank, of sorts... leading to what is arguably the greatest punch-line in history.
|
|
|
|
|
|
|
|
|
|
|
| Reply |
Message 13 of 24 on the subject |
|
|
|
| Reply |
Message 14 of 24 on the subject |
|
|
| Reply |
Message 31 of 31 on the subject |
|
|
| Reply |
Message 71 of 73 on the subject |
|
|
|
|
| Reply |
Message 72 of 73 on the subject |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Geometry of the Great Pyramid
DIMENSIONS of Great Pyramid
by morphvs
The following article is Copyright © 2001-2003 aiwaz.net_institute.
All rights reserved. No part of this website, including text and images, may be reproduced or copied
in any form or by any means without the express prior written permission of aiwaz.net_institute.
Presented with permission.
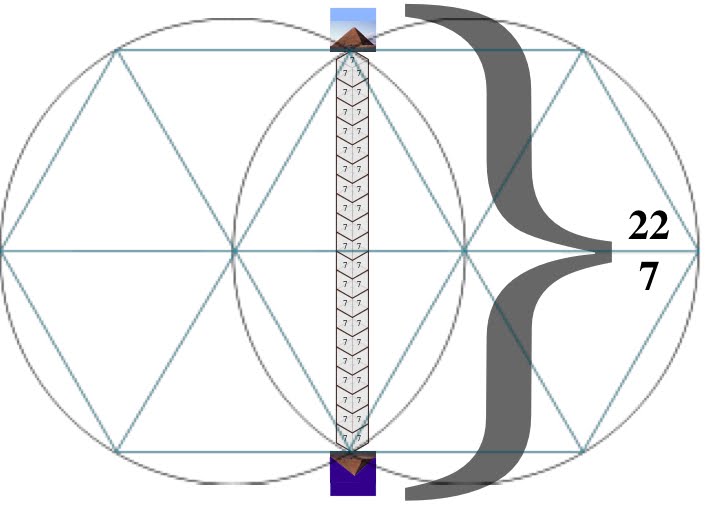
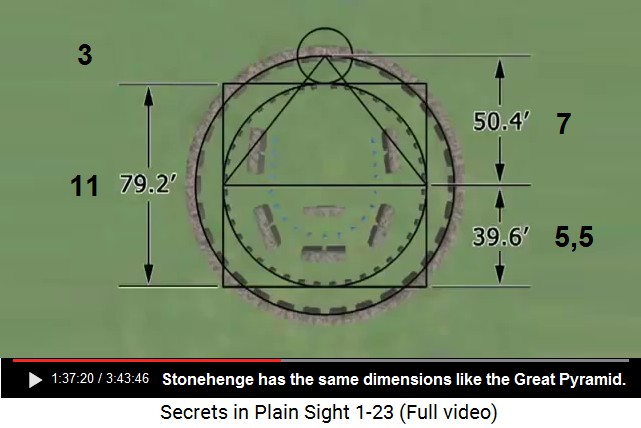
If the calculations concerning the royal cubit are correct the main dimensions of the pyramid should also prove that. The approximate dimensions of the pyramid are calculated by Petrie according to the remains of the sockets in the ground for the casing stones whose remains are still at the top of the pyramid, and the angle 51° 52' ± 2' of the slopes. The base of 9069 inches is approximately 440 royal cubits (the difference is 9 inches which is not a remarkable difference if we consider the whole dimension and consider that the employed data represent only an estimation of the real values) whereas the calculated height, 5776 inches, is precisely 280 royal cubits. The relation 440:280 can be reduced to 11:7, which gives an approximation of the half value of Pi.
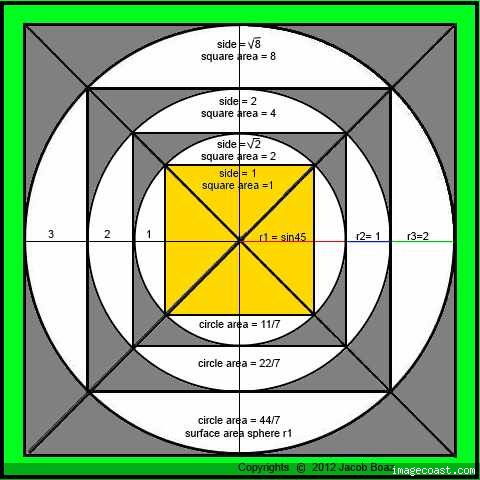
Squaring the Circle

The circle and the square are
united through the circumference:
440x4=1760=2x22/7x280
area of square: 440x440=193600
area of circle:28x28x22/7=246400
sum: 440000
|
The engagement of Pi value in the main dimensions suggests also a very accurate angle of 51° 52' ± 2' of the slopes which expresses the value of Pi. Another coincidence is the relation between the height of the pyramid's triangle in relation to a half of the side of the pyramid, since it appears to be the Golden Section, or the specific ratio ruling this set of proportions, F = (sqr(5)+1)/2 = 1.618 = 356:220. This ratio, 356:220 = 89:55 is also contained in the first of Fibonacci Series:
1 2 3 5 8 13 21 34 55 89 144 ...
A single composition contains two apparently contradicting irrational numbers P and F, without disrupting each other. This appears to be completely opposed to the classical architectural canon which postulates that in 'good' composition no two different geometrical systems of proportions may be mixed in order to maintain the purity of design.
But analysis of other architectural and artistic forms suggested that the greatest masters skillfully juggled the proportional canons without losing the coherent system, for they knew that these systems can be interconnected if the path that links them is found. That is obvious In the case of the Great Pyramid where two different principles are interweaved without interference ruling different angles of the composition, which is most importantly a most simple one, namely 11:7, a most simple ratio obviously signifying such infinite mysteries as the value of P and most 'natural' value of F. In spite of common miss-understanding of architectural composition, the most mysterious and praised compositions are very simple but not devoid of anthropomorphic appeal, since everything is made out of human proportions, just like Vitruvius describing the rations of the human body, very simple and very clean. The numbers 7 and in 11 are successive factors in the second of Fibonacci progressions that approximate geometry of the pentagram:
1 3 4 7 11 18 29 47 76 123 ...
The summary of the selected main mean dimensions is:
|
dimension
|
b. inch
|
m
|
royal cub.
|
palm
|
digit
|
|
base
|
9068.8
|
230.35
|
440
|
3,080
|
12,320
|
|
height
|
5776
|
146.71
|
280
|
1,960
|
7,840
|
|
sum
|
|
|
720
|
|
20,160
|
|
slope
|
7343.2
|
186.52
|
356
|
2,492
|
9,968
|
|
edge
|
8630.4
|
219.21
|
418
|
2,926
|
11,704
|

The main source of all kinds of delusions and speculations about our mythical past for the western man comes of course from Plato. With the myth of Atlantis he planted the necessary seed of mythical Eden, a culture of high intelligence that lived before the known history. If Plato received any wisdom from the ancient Egypt it could perhaps be traced in the canon of numbers that is so latently present throughout his work, but never on the surface. This canon seems to appear in the descriptions of his fantastic cities where everything is most carefully calculated and proportioned. The topic of Plato's Laws is the description of the ideal state called Magnesia which is entirely composed out of the mysterious number 5,040.
The distance* when Earth is closest to Sun (perihelion) is 147x106 km, which is translated into royal cubits 280x109, hinting at the height of the Great pyramid,
280 royal cubits.
The above article comes from aiwaz.net_institute - Great Pyramid and Giza plateau
and is Copyright © 2001-2003 aiwaz.net_institute. All rights reserved.
No part of this article, including text and images, may be reproduced or copied in any form
or by any means without the express prior written permission of aiwaz.net_institute. Reprinted with permission.
* Related links: Astronomic & Cosmographic Data, Nasa site with planetary data
Do not miss this web site: aiwaz.net_institute - Great Pyramid and Giza plateau
Find out more amazing facts about the GREAT PYRAMID: Position of King's Chamber, Queen's Chamber, Subterranean Chamber; SECOND PYRAMID: Dimensions of Pyramid, Great Chamber, Coffer, Lower Chamber; THIRD PYRAMID: Dimensions of Pyramid, Chambers,MATHESIS of Giza Plateau.
The Golden Ratio & Squaring the Circle in the Great Pyramid
A straight line is said to have been cut in extreme and mean ratio when,
as the whole line is to the greater segment, so is the greater to the less. [Euclid]
The extreme and mean ratio is also known as the golden ratio.

If the smaller part = 1, and larger part = G, the golden ratio requires that
G is equal approximately 1.6180
Does the Great Pyramid contain the Golden Ratio?
Assuming that the height of the GP = 146.515 m, and base = 230.363 m, and using simple math
we find that half of the base is 115.182 m and the "slant height" is 186.369 m
Dividing the "slant height" (186.369m) by "half base" (115.182m) gives = 1.6180, which is practically equal to the golden ration!
The earth/moon relationship is the only one in our solar system that contains this unique golden section ratio that "squares the circle". Along with this is the phenomenon that the moon and the sun appear to be the same size, most clearly noticed during an eclipse. This too is true only from earth's vantage point…No other planet/moon relationship in our solar system can make this claim.
Although the problem of squaring the circle was proven mathematically impossible in the 19th century (as pi, being irrational, cannot be exactly measured), the Earth, the moon, and the Great Pyramid, are all coming about as close as you can get to the solution!
If the base of the Great Pyramid is equated with the diameter of the earth, then the radius of the moon can be generated by subtracting the radius of the earth from the height of the pyramid (see the picture below).

Click here to view larger picture.
Also the square (in orange), with the side equal to the radius of the Earth, and the circle (in blue),
with radius equal to the radius of the Earth plus the radius of the moon, are very nearly equal in perimeters:
Orange Square Perimeter = 2+2+2+2=8
Blue Circle Circumference = 2*pi*1.273=8
Note:
Earth, Radius, Mean = 6,370,973.27862 m *
Moon, Radius, Mean = 1,738,000 m.*
Moon Radius divided by Earth Radius = 0.2728 *
* Source: Astronomic and Cosmographic Data
Let's re-phrase the above arguments **

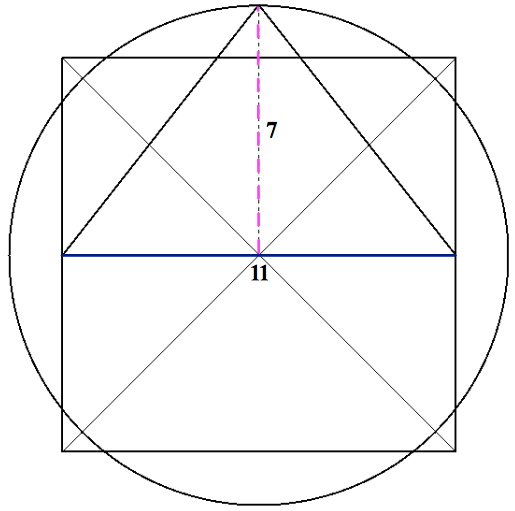
In the diagram above, the big triangle is the same proportion and angle of the Great Pyramid, with its base angles at 51 degrees 51 minutes. If you bisect this triangle and assign a value of 1 to each base, then the hypotenuse (the side opposite the right angle) equals phi (1.618..) and the perpendicular side equals the square root of phi. And that’s not all. A circle is drawn with it’s centre and diameter the same as the base of the large triangle. This represents the circumference of the earth. A square is then drawn to touch the outside of the earth circle. A second circle is then drawn around the first one, with its circumference equal to the perimeter of the square. (The squaring of the circle.) This new circle will actually pass exactly through the apex of the pyramid. And now the “wow”: A circle drawn with its centre at the apex of the pyramid and its radius just long enough to touch the earth circle, will have the circumference of the moon! Neat, huh! And the small triangle formed by the moon and the earth square will be a perfect 345 triangle (which doesn’t seem to mean much.)
** Source: http://geometry.wholesomebalance.com/Sacred_Geometry_2.html#Phi
Recommend this website to your friends:

Was the golden ratio intentionally built into the Great Pyramid of Cheops?
Why would anyone intentionally build the golden ratio into a pyramid, or other structure? What was the significance of to the Egyptians? And did the ancient Egyptians intentionally design the Great Pyramid to square the circle?
The answer to these questions is uncertain since designing the Great Pyramid according to the simple rules explained by the graphic below would give the pyramid automatically (by coincidence? ) all its "magic" qualities.
The height of the Great Pyramid times 2π exactly equals the perimeter of the pyramid. This proportions result from elegant design of the pyramid with the height equal two diameters of a circle and the base equal to the circumference of the circle. Click here or on the image below to see larger picture.



For the angle of the Great Pyramid, any theory of the base, combined with any theory of the height, yields a theoretic angle; but the angles actually proposed are the following** :
|
Angle of casing measured
By theory of 34 slope to 21 base
Height : circumference :: radius to circle
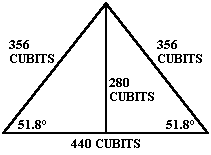
9 height on 10 base diagonally
7 height to 22 circumference
area of face = area of height squared
(or sine) = cotangent, and many other relations)
2 height vertical to 3 height diagonal
5 height on 4 base
|
51º 52' ± 2' (51.867)
51º 51' 20"
51º 51' 14.3"
51º 50' 39.1"
51º 50' 34.0"
51º 49' 38.3"
51º 40' 16.2"
51º 20' 25"
|
** Page 184, The Pyramids and Temples of Gizeh
by Sir W.M.Flinders Petrie 1883
Giza Alignment Code - The Time Temple
A silent message from 5000 years ago. From a letter to a scientist:
"The conclusion should be made upon a probability, that it may be just coincidental, that these 14 lines are forming a very accurate model of the inner planetary system, showing also a precise time position, that coincidentally matches (relative to the end of Mayan Calendar) the beginning of the final 1260 days time period, mentioned both in the Old and New Testament (surely one of the most remarkable and disputed episodes in the Book), a time period, which allows (and was supposedly measured for) to show in a relatively short period of time, when, and what the End is all about - the mystery of death and the origin of life.
http://old.world-mysteries.com/mpl_2.htm
|
|
|
|
|
|
| Reply |
Message 17 of 24 on the subject |
|
|
|
| Reply |
Message 18 of 24 on the subject |
|
|
|
|
|
|
|
|
Génesis 7
1. Dijo luego Jehová a Noé: Entra tú y toda tu casa en el arca; porque a ti he visto justo delante de mí en esta generación.
2. De todo animal limpio tomarás siete parejas, macho y su hembra; mas de los animales que no son limpios, una pareja, el macho y su hembra.
3. También de las aves de los cielos, siete parejas, macho y hembra, para conservar viva la especie sobre la faz de la tierra.
4. Porque pasados aún siete días, yo haré llover sobre la tierra cuarenta días y cuarenta noches; y raeré de sobre la faz de la tierra a todo ser viviente que hice.
5. E hizo Noé conforme a todo lo que le mandó Jehová.
6. Era Noé de seiscientos años cuando el diluvio de las aguas vino sobre la tierra.
7. Y por causa de las aguas del diluvio entró Noé al arca, y con él sus hijos, su mujer, y las mujeres de sus hijos.
8. De los animales limpios, y de los animales que no eran limpios, y de las aves, y de todo lo que se arrastra sobre la tierra,
9. de dos en dos entraron con Noé en el arca; macho y hembra, como mandó Dios a Noé.
10. Y sucedió que al séptimo día las aguas del diluvio vinieron sobre la tierra.
11. El año seiscientos de la vida de Noé, en el mes segundo, a los diecisiete días del mes, aquel día fueron rotas todas las fuentes del grande abismo, y las cataratas de los cielos fueron abiertas,
EN EL CONTEXTO A LA LUNA NUEVA EN LUNA LLENA, EL DIECISIETE NOS CAE EN LUNA CRECIENTE.
12. y hubo lluvia sobre la tierra cuarenta días y cuarenta noches.
13. En este mismo día entraron Noé, y Sem, Cam y Jafet hijos de Noé, la mujer de Noé, y las tres mujeres de sus hijos, con él en el arca;
14. ellos, y todos los animales silvestres según sus especies, y todos los animales domesticados según sus especies, y todo reptil que se arrastra sobre la tierra según su especie, y toda ave según su especie, y todo pájaro de toda especie.
15. Vinieron, pues, con Noé al arca, de dos en dos de toda carne en que había espíritu de vida.
16. Y los que vinieron, macho y hembra de toda carne vinieron, como le había mandado Dios; y Jehová le cerró la puerta.
17. Y fue el diluvio cuarenta días sobre la tierra; y las aguas crecieron, y alzaron el arca, y se elevó sobre la tierra.
18. Y subieron las aguas y crecieron en gran manera sobre la tierra; y flotaba el arca sobre la superficie de las aguas.
19. Y las aguas subieron mucho sobre la tierra; y todos los montes altos que había debajo de todos los cielos, fueron cubiertos.
20. Quince codos más alto subieron las aguas, después que fueron cubiertos los montes.
21. Y murió toda carne que se mueve sobre la tierra, así de aves como de ganado y de bestias, y de todo reptil que se arrastra sobre la tierra, y todo hombre.
22. Todo lo que tenía aliento de espíritu de vida en sus narices, todo lo que había en la tierra, murió.
23. Así fue destruido todo ser que vivía sobre la faz de la tierra, desde el hombre hasta la bestia, los reptiles, y las aves del cielo; y fueron raídos de la tierra, y quedó solamente Noé, y los que con él estaban en el arca.
24. Y prevalecieron las aguas sobre la tierra ciento cincuenta días.
|
| Reply |
Message 58 of 58 on the subject |
|
Génesis 8
1. Y se acordó Dios de Noé, y de todos los animales, y de todas las bestias que estaban con él en el arca; e hizo pasar Dios un viento sobre la tierra, y disminuyeron las aguas.
2. Y se cerraron las fuentes del abismo y las cataratas de los cielos; y la lluvia de los cielos fue detenida.
3. Y las aguas decrecían gradualmente de sobre la tierra; y se retiraron las aguas al cabo de ciento cincuenta días.
4. Y reposó el arca en el mes séptimo, a los diecisiete días del mes, sobre los montes de Ararat.
5. Y las aguas fueron decreciendo hasta el mes décimo; en el décimo, al primero del mes, se descubrieron las cimas de los montes.
6. Sucedió que al cabo de cuarenta días abrió Noé la ventana del arca que había hecho,
7. y envió un cuervo, el cual salió, y estuvo yendo y volviendo hasta que las aguas se secaron sobre la tierra.
8. Envió también de sí una paloma, para ver si las aguas se habían retirado de sobre la faz de la tierra.
9. Y no halló la paloma donde sentar la planta de su pie, y volvió a él al arca, porque las aguas estaban aún sobre la faz de toda la tierra. Entonces él extendió su mano, y tomándola, la hizo entrar consigo en el arca.
10. Esperó aún otros siete días, y volvió a enviar la paloma fuera del arca.
11. Y la paloma volvió a él a la hora de la tarde; y he aquí que traía una hoja de olivo en el pico; y entendió Noé que las aguas se habían retirado de sobre la tierra.
12. Y esperó aún otros siete días, y envió la paloma, la cual no volvió ya más a él.
13. Y sucedió que en el año seiscientos uno de Noé, en el mes primero, el día primero del mes, las aguas se secaron sobre la tierra; y quitó Noé la cubierta del arca, y miró, y he aquí que la faz de la tierra estaba seca.
14. Y en el mes segundo, a los veintisiete días del mes, se secó la tierra. (AQUI ESTA LA CLAVE MATEMATICA DEL "EXPERIMENTO FILADELFIA" EN EL CONTEXTO AL "ARCA DE NOE". 2/27 EN UN MARCO AL CALENDARIO LUNAR. ESTO EXPLICA LA FUERTE CONNOTACION MARITIMA DEL MISMO. ES QUE EN REALIDAD EL "ARCA DE NOE" TAMBIEN TIENE FUERTE CONNOTACION CON EL "AGUJERO DE GUSANO".)
15. Entonces habló Dios a Noé, diciendo:
16. Sal del arca tú, y tu mujer, y tus hijos, y las mujeres de tus hijos contigo.
17. Todos los animales que están contigo de toda carne, de aves y de bestias y de todo reptil que se arrastra sobre la tierra, sacarás contigo; y vayan por la tierra, y fructifiquen y multiplíquense sobre la tierra.
18. Entonces salió Noé, y sus hijos, su mujer, y las mujeres de sus hijos con él.
19. Todos los animales, y todo reptil y toda ave, todo lo que se mueve sobre la tierra según sus especies, salieron del arca.
20. Y edificó Noé un altar a Jehová, y tomó de todo animal limpio y de toda ave limpia, y ofreció holocausto en el altar.
21. Y percibió Jehová olor grato; y dijo Jehová en su corazón: No volveré más a maldecir la tierra por causa del hombre; porque el intento del corazón del hombre es malo desde su juventud; ni volveré más a destruir todo ser viviente, como he hecho.
22. Mientras la tierra permanezca, no cesarán la sementera y la siega, el frío y el calor, el verano y el invierno, y el día y la noche.
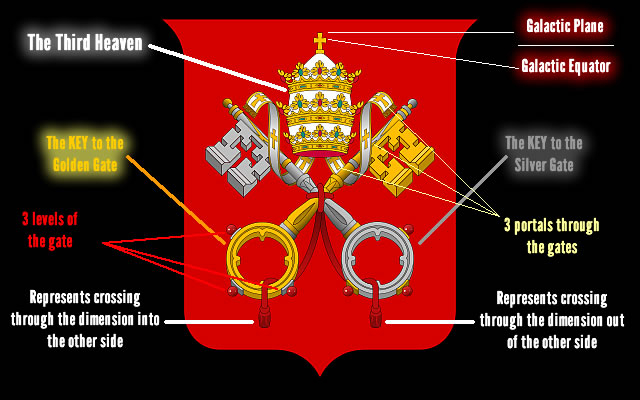
Noten la clave NUMERO OCHO Y EL NUMERO CUATRO, EL MISMO PATRON DEL VATICANO.
Do you notice the symbolic 8 rays within the circle? Symbolic of the star Sirius.
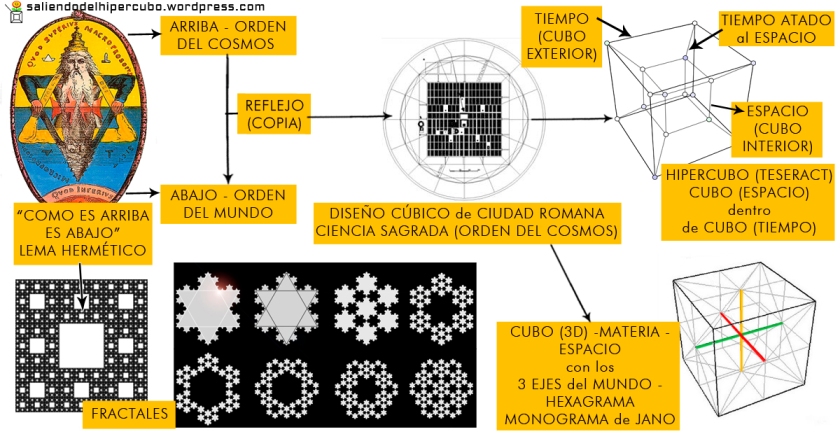
LA MISMA PIRAMIDE DEL VATICANO, AL ESTAR DISEÑADA EN FUNCION A SIRIO, Y A SU NEXO CON EL ESTE, OESTE, NORTE Y SUR, OSEA LAS CUATRO ORIENTACIONES, ES UNA REFERENCIA A LA "MAQUINA DEL TIEMPO". POR ESA CAUSA ESTA ADENTRO DE LA CERRADURA Y TIENE RELACION CON LA LLAVE DE DAVID "EXPERIMENTO FILADELFIA".
2. Isaías 22:22: Y pondré la LLAVE de la casa de David sobre su hombro; y abrirá, y nadie cerrará; cerrará, y nadie abrirá.
3. Mateo 16:19: Y a ti te daré las LLAVEs del reino de los cielos; y todo lo que atares en la tierra será atado en los cielos; y todo lo que desatares en la tierra será desatado en los cielos.
4. Lucas 11:52: ¡Ay de vosotros, intérpretes de la ley! porque habéis quitado la LLAVE de la ciencia; vosotros mismos no entrasteis, y a los que entraban se lo impedisteis.
5. Apocalipsis 1:18: y el que vivo, y estuve muerto; mas he aquí que vivo por los siglos de los siglos, amén. Y tengo las LLAVEs de la muerte y del Hades.
6. Apocalipsis 3:7: Escribe al ángel de la iglesia en Filadelfia: Esto dice el Santo, el Verdadero, el que tiene la LLAVE de David, el que abre y ninguno cierra, y cierra y ninguno abre:
EL DIA Y LA NOCHE ES UNA REFERENCIA A LAS 24 HORAS, OSEA A LA SANTA CENA.
DIA / SOL/ HOMBRE / ORO / PAN / CUADRADO
NOCHE / LUNA/ MUJER / PLATA / VINO / CIRCULO
HECHOS 12:12 (JUAN MARCOS ES EL GRIAL)
|
|
|
|
|
|
|
Teniendo en cuenta que el radio de la tierra promedio es de 7*12*12*12*12*12*12, la longitud de la circunferencia en este marco es de 44*12*12*12*12*12*12 tambien en pies ingleses. Osea que si cuadramos la LONGITUD DE LA CIRCUNFERENCIA DE LA TIERRA, TENEMOS UN CUADRADO CUYO LADO ES DE 11*12*12*12*12*12*12. VEMOS QUE AQUI TAMBIEN TENEMOS EL ORIGEN DE LA RELACION 11/7, CODIFICADA EN LA GRAN PIRAMIDE. |
|
|
|
|
Sólido de Kepler-Poinsot
Los sólidos de Kepler-Poinsot con sus símbolos de Schläfli.
Un sólido de Kepler (también llamado sólido de Kepler-Poinsot) es un poliedro regular no convexo, cuyas caras son todas polígonos regulares y que tiene en todos sus vértices el mismo número de caras concurrentes (compárese con los sólidos platónicos).
Existen sólo cuatro tipos, con las denominaciones siguientes:
Las caras están solo parcialmente en la superficie del sólido, y las partes expuestas están sólo conectadas en puntos (si están conectadas de algún modo). Si las partes se cuentan como caras separadas, el sólido deja de ser regular.
Características
Un sólido de Kepler cubre su esfera circunscrita más de una vez (con una esfera interior y otra exterior), con los centros de las caras como puntos direccionales en los sólidos que tienen caras en forma de pentagrama, mientras que en los otros son los vértices los que cumplen esa función. Por esta razón, no son necesariamente equivalentes topológicos de la esfera como lo son los sólidos platónicos, y en particular la característica de Euler V − E + F = 2 se verifica solamente para el Gran dodecaedro estrellado y para el Gran icosaedro.
Esto dependerá de cómo se observe el poliedro. Considérese, por ejemplo, el pequeño dodecaedro estrellado.1 Consiste en un dodecaedro con una pirámide pentagonal en cada una de sus 12 caras. En consecuencia, las 12 caras se extienden a pentagramas con el pentágono central dentro del sólido. La parte externa de cada cara consiste en cinco triángulos conectados por sólo cinco puntos. Si se cuentan separadamente, hay 60 caras (pero estas son triángulos isósceles que no son polígonos regulares, en cuyo caso seria un pentaquisdodecaedro). De modo similar, cada lado puede ser contado como tres, pero entonces los habrá de dos tipos. Igualmente, con los "cinco puntos" antes mencionados: en total habrá 20 puntos que pueden contarse como vértices, por lo que habrá un total de 32 vértices (otra vez, de dos tipos). Ahora la ecuación de Euler se verifica: 60 - 90 + 32 = 2.
Tipos
Hay cuatro sólidos de Kepler distintos:
Los dos primeros son estrellamientos, es decir, sus caras son convexas. Los otros dos tienen caras cóncavas, pero cada par de caras que se encuentra en un vértice de hecho lo hace en dos.
Historia
Mosaico del suelo en la basílica de San Marcos, a veces atribuido a Paolo Uccello.
La mayoría de los poliedros de Kepler-Poinsot, si no todos, eran ya conocidos de una forma u otra antes de Kepler. Un pequeño dodecaedro estrellado aparece en una tarsia de mármol (panel de incrustaciones) en el suelo de la basílica de San Marcos de Venecia, Italia. Data del siglo XV y, a veces se atribuye a Paolo Uccello. Wenzel Jamnitzer, en su obra Perspectiva corporum regularium (Perspectivas de los sólidos regulares), un libro de grabados en madera publicado en el siglo XVI, representa el gran dodecaedro y el gran dodecaedro estrellado.2 Se desprende de la disposición general del libro que consideraba solamente los cinco sólidos platónicos como regulares, y no comprendía la naturaleza periódica de sus grandes dodecaedros.
El pequeño y gran dodecaedro estrellado, a veces llamados poliedros de Kepler, fueron reconocidos por primera vez como regulares por Johannes Kepler en 1619, cuando notó que los dodecaedros estrellados (tanto el grande como el pequeño) se componían de dodecaedros "ocultos" (con caras pentagonales) que tienen caras compuestas de triángulos, tomando la apariencia de estrellas estilizadas. Los obtuvo por estelación del dodecaedro regular convexo, por primera vez, tratándolo como una superficie en lugar de un sólido. Se dio cuenta de que extendiendo los bordes o caras del dodecaedro convexo hasta que se encontrasen de nuevo, se podían obtener pentágonos estrellados. De esta manera construyó los dos dodecaedros estrellados, cada uno con la región convexa central de cada cara "oculta" en el interior, sólo con los brazos triangulares visibles. El paso final de Kepler fue reconocer que estos poliedros se ajustaban a la definición de regularidad, aunque fueran cóncavos en lugar de convexos, como sí lo eran los tradicionales sólidos platónicos.
En 1809, Louis Poinsot redescubrió las figuras de Kepler, mediante el ensamblaje de pentágonos estrellados alrededor de cada vértice. También montó polígonos convexos alrededor de los vértices de las estrellas para descubrir dos estrellas más regulares, el gran icosaedro y el gran dodecaedro. Por ello, algunos llaman a estos dos los poliedros de Poinsot. Poinsot no sabía si había descubierto todos los poliedros regulares estrellados.
Tres años más tarde, Augustin Cauchy demostró que la lista por estelación de los sólidos platónicos estaba completa, y casi medio siglo después, en 1858, Joseph Louis François Bertrandproporcionó una prueba más elegante por facetado de ellas.
Al año siguiente, Arthur Cayley dio a los poliedros de Kepler–Poinsot los nombres por los que generalmente conocidos hoy.
Unos cien años más tarde, John Conway desarrolló una terminología sistemática para las estelaciones hasta un máximo de cuatro dimensiones. Dentro de este esquema, sugirió nombres ligeramente modificados para dos de los poliedros regulares estrellados. Los nombres de Conway han sido considerados de utilidad, pero no han sido ampliamente adoptados.
| Nombre de Cayley |
pequeño dodecaedro estrellado |
gran dodecaedro |
gran dodecaedro estrellado |
gran icosaedro |
| Nombre de Conway |
dodecaedro estrellado |
gran dodecaedro (sin cambio) |
dodecaedro grande estrellado |
gran icosaedro (sin cambio) |
https://es.wikipedia.org/wiki/S%C3%B3lido_de_Kepler-Poinsot |
|
|
 First First  Previous 2 to 5 of 5 Next Previous 2 to 5 of 5 Next  Last Last  |
|
|
Posted in Azulejos-Mosaicos, Italia, Templo with tags Poliedros on 7 junio 2012 by angelrequena

Hace tiempo hablamos del conocido pequeño dodecaedro estrellado del pavimento de la puerta de salida derecha del duomo de San Marcos. No es el único de la catedral veneciana: apenas visible para la visita ordinaria hay otro más pequeño, justo debajo del iconostasio en su centro, en lugar preferente y en línea con el altar.
Si se entra hacia la Pala de Oro puede verse una mancha central en la lejanía pero casi sin distinguirse. En mi última visita tuve la gran suerte de encontrar un ordenanza amable que encendía las luces a un grupo concertado que me permitió verlo y fotografiarlo. No desmerece de su hermano mayor, si cabe revela mayor virtuosismo y ostentación del dominio de la perspectiva matemática.
Hay cuatro sólidos regulares cóncavos, los dos de Poinsot y los dos de Kepler. Venecia nos ofrece los dos de Kepler en San Pantaleone y uno en San Marcos pero en dos lugares, uno alejado para despedirse del templo y otro en el lugar más destacado: la entrada central al recinto más sagrado.
El dodecaedro estrellado de la puerta (abajo) solo tiene una corona de taracea marmórea complementaria mientras que el del iconostasio (arriba) tiene tres.

3 Comments »
https://mateturismo.wordpress.com/tag/poliedros/page/7/
|
|
|
|
|
|
|
|
. Juan 16:21 La mujer cuando da a luz, tiene dolor, porque ha llegado su HORA; pero después que ha dado a luz un niño, ya no se acuerda de la angustia, por el gozo de que haya nacido un hombre en el mundo.
|
|
|
|
|
¿COMO EXPLICAS EL NEXO 911 CON EL DIA DE MARIA MAGDALENA EN EL MARCO A LA INDEPENDENCIA DE EEUU EN FILADELFIA?
11/9/2001-11/9/2005=1461 DIAS
11/9/2005-22/7/2006=315 DIAS
1461+315=1776
EL 4/7/1776=INDEPENDENCIA DE EEUU EN FILADELFIA
En aquel tiempo, respondiendo Jesús, dijo:
Te alabo, Padre, Señor del cielo y de la tierra,
que hayas escondido estas cosas (la Gnosis, la Sabiduría Oculta)
de los sabios (de los eruditos) y de los entendidos, (de los intelectuales)
y las hayas revelado á los niños. (A los Iniciados). Así, Padre, pues que así agradó en tus ojos."
(Mateo 11: 25-26).
EL PATRON KAVALISTICO DE LA INDEPENDENCIA DE LOS ESTADOS UNIDOS ESTA TOTALMENTE INTERRELACIONADO CON LAS BODAS DE CANA, EN EL CONTEXTO A QUE LA MISMA NO FUE SOLAMENTE EN UN TERCER DIA ( JUAN 2:1), SINO QUE TAMBIEN EN UN SEPTIMO DIA (JUAN 1:29,35,42 Y JUAN 2:1). DE ALLI SALE EL MONSTRUSO NUMERO 37.
1776=48*37
666=37*18
37*18=666
37*48=1776 (AÑO DE LA INDEPENDENCIA DE EEUU)
LA MISMA TORRE ES UN SIMBOLO FALICO CON FUERTE CONNOTACION SEXUAL
|
|
|
|
|
EL MASONICO "SECRETO MASONICO" DETRAS DE LA MANZANA (EN EL LIBRO DE JOB) /STEVE JOBS, CREADOR DE APPLE

drjudywood.com
The WTC twin towers towering
800 × 600 - 84k - jpg |

en.wikipedia.org
to the World Trade Center,
4256 × 3426 - 12407k - jpg |
Job
25:1 Respondió Bildad suhita, y dijo:
25:2 El señorío y el temor están con él; El hace paz en sus alturas.
25:3 ¿Tienen sus ejércitos número? ¿Sobre quién no está su luz?
25:4 ¿Cómo, pues, se justificará el hombre para con Dios? ¿Y cómo será limpio el que nace de mujer?
25:5 He aquí que ni aun la misma luna será resplandeciente, Ni las estrellas son limpias delante de sus ojos;
25:6 ¿Cuánto menos el hombre, que es un gusano, Y el hijo de hombre, también gusano?
agujero blanco=hombre=boaz
agujero negro=mujer=jachin
salmo 119 (alfa y el omega)
entre los mismos hay un obvio "agujero de gusano"
el hijo, es el OBVIO "AGUJERO DE GUSANO"
LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
|
|
|
 Primeira
Primeira
 Anterior
2 a 14 de 29
Seguinte
Anterior
2 a 14 de 29
Seguinte Última
Última
|
|
| |
|
|
©2025 - Gabitos - Todos os direitos reservados | |
|
|





 [3d:2d = 343 : 127 ]
[3d:2d = 343 : 127 ]








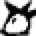
















































































































![Back To The Future: 15 Years Of Apple Web Design Seen Through A Time Machine [Feature] backtothefutureiphone](http://cdn.cultofmac.com/wp-content/uploads/2013/01/backtothefutureiphone.jpg)