Nada es verdad, ni mentira dicen algunos, y terminan la frase atribuyendo la causa de la posible diferencia en el punto de vista al color del cristal con que se mira. Puede ser… En este sentido siempre he sido más de Descartes y su Discurso del Método:
no admitir como verdadera cosa alguna, como no supiese con evidencia que lo es; es decir, evitar cuidadosamente la precipitación y la prevención, y no comprender en mis juicios nada más que lo que se presentase tan clara y distintamente a mí espíritu, que no hubiese ninguna ocasión de ponerlo en duda.
No, no estoy hablando de rescates, no tengo ganas de entrar en debates nominalistas, yo tampoco.
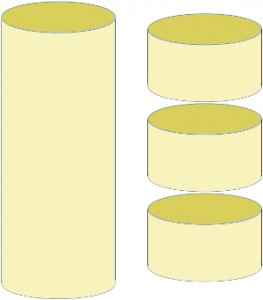 Imaginen que quieren construir unos depósitos de combustible cilíndricos de gran capacidad, por ejemplo para un transbordador espacial. Imaginen que para ello lo construyen en varias trozos cilíndricos que luego encajarán unos con otros, formando el depósito cilíndrico final.
Imaginen que quieren construir unos depósitos de combustible cilíndricos de gran capacidad, por ejemplo para un transbordador espacial. Imaginen que para ello lo construyen en varias trozos cilíndricos que luego encajarán unos con otros, formando el depósito cilíndrico final.
Parece evidente que es importante que las distintas partes encajen bien entre sí, es decir, que la base de dichos cilindros midan todas lo mismo, y sobre todo, que sean círculos perfectos. Digo yo que una fuga de combustible puede resultar, cuanto menos, inapropiada ¿Cómo comprobar esto último? Es decir, ¿cómo comprobamos que la base del cilindro es un círculo perfecto?
Uno podría pensar que si mide un número alto de diámetros distintos de la base y todos miden lo mismo, eso tiene que ser un círculo, ¿no?
¿Cuántos diámetros medimos? Yo que sé… 100.000 millones por ejemplo. Si, total, hay infinitos diámetros en un círculo… ¿Podemos estar seguros de que si los 100.000 millones de diámetros miden lo mismo lo que estamos midiendo es un círculo?
Si en lugar de depósitos gigantescos de combustible medimos tubos, ¿nos servirá un calibrador de fontanero para saber si efectivamente el tubo es perfectamente circular? Si lo abrimos con una apertura concreta y lo hacemos girar alrededor de nuestro tubo, eso tiene que ser redondo, ¿no? ¿Sí?
Si respondemos afirmativamente a las dos preguntas finales de los dos parrafos anteriores es porque estamos asumiendo que una figura geométrica con la propiedad de ser igual de ancha en todas las direcciones es un círculo ¿Sí?
En geometría, se llama anchura de un conjunto en el plano a la menor distancia entre 2 rectas paralelas que lo encierran, es decir, la anchura de un objeto es la del pasillo más estrecho en el que cabe. Con esta definición, lo que estaríamos afirmando respondiendo sí a las preguntas anteriormente mencionadas es que un conjunto que tenga anchura constante, la misma en todas las direcciones, es un círculo ¿Sí?
Vamos ver qué pasa con otras figuras planas conocidas. Un triángulo por ejemplo, tiene ¿anchura constante?
Pues como se ve en la figura anterior, si calibramos por el lado del triángulo la medida es mayor que si calibramos desde uno de los lados al vértice opuesto. No nos sirve…
 ¿Y un cuadrado? ¿Tiene anchura constante?
¿Y un cuadrado? ¿Tiene anchura constante?
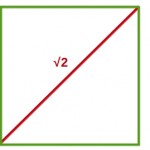
Vaya, pues parece que tampoco. Porque en el cuadrado de la figura, un cuadrado de lado 1, si lo calibramos de lado a lado medirá exatcamente eso, 1, y si lo calibramos según una diagonal 8en rojo en la figura) medirá
√2.
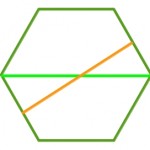 ¿Y un hexágono? ¿Será una figura de anchura constante? No sé, parece más redondito…
¿Y un hexágono? ¿Será una figura de anchura constante? No sé, parece más redondito…
Tampoco, como se aprecia en la figura de la derecha. si calibramos en la dirección perpendicular a la línea verde, la medida es mayor que cuando calibramos en perpendicular a la línea de color naranja.
Esto puede inducir a pensar que efectivamente, como habíamos sospechado, la única figura geométrica plana que tiene anchura constante es un círculo, ¿verdad?
Pues no. Existen otras figuras, infinitas de hecho, que tienen anchura constante y que no son círculos. Lo cual puede ser un poco chungo en el caso de las piezas del depósito de combustible de un transbordador espacial. Estas posibles pequeñas imperfecciones en el encaje se resuelven usando juntas tóricas (con forma de flotador) de goma que lo amortigüen. Ahora, eso sí, hay que asegurarse de que estas juntas estén fabricadas con un material adecuado y que, por ejemplo, no sean demasiado sensibles a los cambios de temperaturas y esas cosas, no sea que nos pase como pasó con el Challenger*… y eso no está bonito.
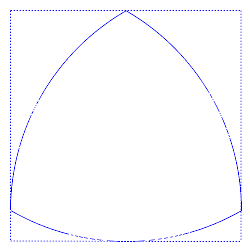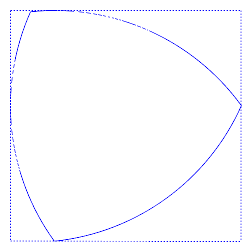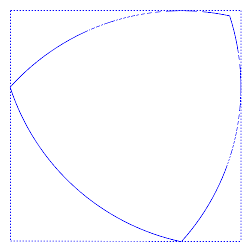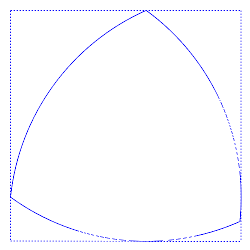
Efectivamente, una de las figuras de anchura constante más conocidas son los polígonos de Reuleaux, que reciben este nombre en honor del ingeniero alemán que los desarrolló, Franz Reuleaux. Vamos a fijarnos por ejemplo en el más simple de estos polígonos de anchura constante, el triángulo de Reuleaux.
Efectivamente, este tipo de triángulos tiene anchura constante. Si lo medimos con el calibrador, en cualquier dirección obtenemos el mismo resultado. Y, evidentemente no son círculos
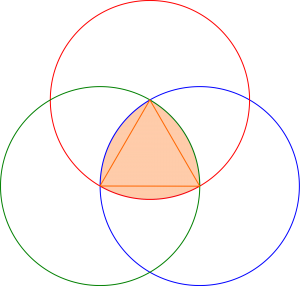 ¿Cómo se dibuja un triángulo de Reuleaux?
¿Cómo se dibuja un triángulo de Reuleaux?
Basta comenzar con un triángulo equilátero. Ahora, con un compás, nos apoyamos en cada uno de los 3 vértices de dicho triángulo, y trazamos el arco de circunferencia que une los otros dos vértices.
¿Qué interés, aparte de ser de anchura constante, puede tener un polígono de Reuleaux en general, o un triángulo de éstos en particular?
Por ejemplo, para el diseño de tapas de alcantarilla. Ya, ya sé que con hacerlas circulares se resuelve el problema, pero nunca hay que renunciar a mejorar un poco los pequeños detalles de la vida con el fin de hacerlo más bonito o, al menos diferente. Si diseñamos una tapa de alcantarilla con esta forma, como cualquier posición tiene el mismo ancho, la tapa así diseñada nunca se caería hacia dentro, no habría forma de meterla. Mientras que si, por ejemplo la tapa fuese cuadrada, bastaría con levantarla, y colarla derechita, usando la diagonal del hueco que es siempre mayor que el lado del cuadrado.
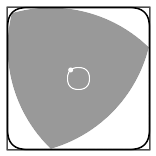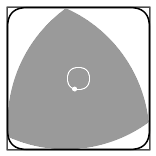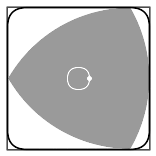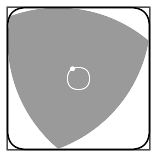
Además de tapas de alcantarillas, los triángulos de Reuleaux se han usado para el diseño de una taladradora que hace agujeros casi cuadrados. Como se ve en la animación de la izquierda, en las esquinas que da un poco de área sin recubrir por lo que el resultado es un cuadrado con las esquienas redondeadas. El diseño de este taladro inspirado en los triángulos de Reuleaux lleva la firma de Harry James Watts que lo inventó en 1914.
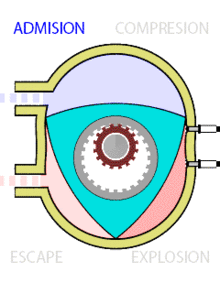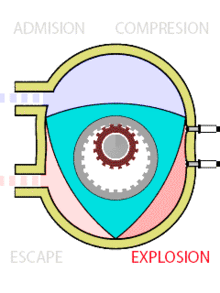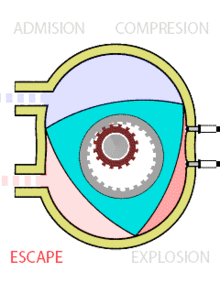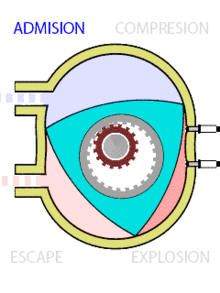
También en el diseño de motores de coches se han usado los triángulos de Reuleaux. Bueno, casi se han usado… Porque en realidad, los triángulos que se usan en el diseño de los rotores del motor Wankel, tienen los lados un poco más aplanados que los triángulos de Reuleaux y, por tanto, no tienen anchura constante. La ventaja de usar este tipo de rotores en lugar de los pistones habituales, permiten que el motor Wankel sea más silencioso, suave y fiable.
Pero no queda ahí la cosa, no, porque como dijo aquel torero, hay gente pa tó… Aunque ya había podido comprobar que una bicicleta, ésta de era de juguete, podía rodar suavemente si sus ruedas eran triángulos de Reuleaux, de hecho nos regalaron una a cada uno de los participantes en el Kyoto CGGT 2007 (celebrado en honor de Jin Akiyama and Vašek Chvátal),
poco después. Guan Baihua en 2009, diseñó una bicicleta donde la rueda de delante era un pentágono de Reuleaux y la de detrás un triángulo del mismo.
Como cuestión estética, los polígonos de Reuleaux aparecen en el diseño de monedas, en la arquitectura…
Lo dejamos por aquí y os invito a que busquéis más apariciones de los polígonos de Reuleaux. Sólo un par de cosas más. La primera es que como dije casi al principio de esta entrada, hay infinitas figuras que tienen anchura constante y es cierto. En este enlace se explica detalladamente una forma de generarlas.



































![sin left ( phi+ heta ight) = cos left [ frac{pi}{2}-(phi + heta) ight]](http://upload.wikimedia.org/math/e/0/1/e019f1b37fae113e7b5a164fcccf7069.png)
![sin left ( phi+ heta ight) = cos left [ left ( frac{pi}{2}-phi ight ) - heta ight ]](http://upload.wikimedia.org/math/d/d/b/ddb3c0c89dd12ca03cd8665e97d97109.png)


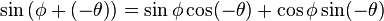


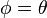 entonces:
entonces: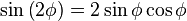

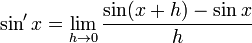
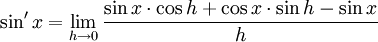
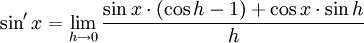
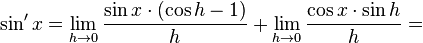

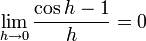

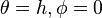 tenemos que:
tenemos que: