|
|
General: Ese Saber, Pitagorico
Elegir otro panel de mensajes |
|
|
| De: Alcoseri (Mensaje original) |
Enviado: 30/09/2012 13:09 |
Ese saber, Pitágoras lo trajo de Egipto Enviado: 01/09/2006 08:46 p.m. Jacques Monnerie no despegó la vista del ejemplar del Picatrix durante buena parte del trayecto por carretera hasta Amiens. A bordo del confortable Mercedes 190 E que la Fundación Charpentier había puesto a su disposición, tuvo tiempo suficiente para hacerse una idea global acerca del contenido del libro. Se trataba, como se temía, de un abigarrado tratado medieval de magia en el que se enseñaba a su propietario a fabricar amuletos. Al principio, le pareció uno de tantos volúmenes simplistas que debieron de circular por Europa entre los siglos XII y XIII, y en el que se contenían fórmulas absurdas para conseguir el amor de la persona deseada, o riqueza y prosperidad para quien supiera manejarlas. Constaba de cuatro tratados o partes, a cual más confusa. Sus referencias históricas a titanes que gobernaban Nubia o a reyes todopoderosos en Egipto no se ajustaban a nada de lo que él había estudiado en el Bachillerato, y por si fuera poco, su conocimiento del Sistema Solar, al que hacía frecuentísimas menciones, se reducía — lógico, por otra parte— sólo a los siete planetas conocidos entonces. Cansado de leer estupideces, cuando iba a dar carpetazo definitivo al Picatrix y recostarse sobre los asientos de cuero del Mercedes, encontró un pasaje que le llamó la atención. En realidad, esperaba encontrar algo como aquello desde que salió del despacho del señor Charpentier. Algo que justificara el interés de su mecenas para que leyera el libro. El pasaje en cuestión afirmaba que los coptos eran los herederos de los antiguos egipcios en cuestiones religiosas y, así mismo, en el manejo de sus poderosos talismanes mágicos. Hasta ahí, eso era bastante razonable. Pero decía, además, que sus amuletos, contrariamente a lo que pensaba, no se reducían a simples medallitas como la de Catalina de Médicis o a pedazos de pergamino con símbolos «de poder» escritos sobre ellos, sino que también podían enmascararse tras la construcción de grandes edificios e incluso en la distribución geométrica de las ciudades. Todo dependía, básicamente, de las alineaciones estelares a las que se orientaran sus cimentaciones. —¡Como París! —barruntó, recordando su cita en los Campos Elíseos. El libro decía, además, cosas tan llamativas como ésta: «En la construcción de ciudades —leyó— hay que utilizar las estrellas, y en la construcción de las casas los planetas; toda ciudad que se construya con Marte en medio del cielo o cualquier estrella fija de la misma naturaleza, verá morir a filo de espada a la mayoría de sus gobernantes». Picatrix se refería igualmente a una ciudad levantada por el propio Hermes «que tenía doce millas de largo y donde hizo una ciudadela con cuatro puertas, una por cada punto». Y seguía: «En la puerta oriental hizo la imagen de un águila. En la puerta occidental, la de un toro. En la septentrional, la de un león. En la austral, la de un perro alado». El ingeniero se extrañó: ¿no eran aquéllas las imágenes que tradicionalmente se asociaban a los cuatro evangelistas? ¿No se equiparaba a Juan con un águila, a Lucas con un toro, a Marcos con un león y a Mateo con un ser alado? Fue lo último que leyó. Picatrix volvía a perderse en divagaciones absurdas sobre el poder de los supertalismanes, que nadie con dos dedos de frente podría tomar nunca en consideración. Sin embargo, como si aquel último pasaje fuera parte de uno de esos acertijos sin solución posible, Monnerie se amodorró preguntándose si no pretendería el señor Charpentier hacerle creer que la catedral de Amiens, ciertamente la mayor de toda Francia, era algo así como el nuevo templo de Hermes del Picatrix. «Demasiado sutil», pensó. No obstante, lo cierto era que las catedrales también se orientaban hacia los cuatro puntos cardinales y a veces colocaban evangelistas en sus fachadas. El chófer entró en Amiens por la avenida Port d’Aval a eso de las seis de la tarde. Enfiló su prolongación por la rue des Francs Muriers, sembrada de casas unifamiliares de tres plantas y estilo dieciochesco, y torció por la rue Saint Leu hasta desembocar frente a la fachada principal de la inmensa seo de la ciudad. Tras aparcar junto a una casa de madera que se caía a pedazos, y donde podía leerse el equívoco cartel de Maison du Pélerin, despertó a Monnerie. —Señor —dijo, pellizcándole el brazo—. Ya hemos llegado. El ingeniero jefe se desperezó como pudo, incorporándose a duras penas en su asiento. Cuando vio la cara oeste de Amiens parcialmente cubierta de andamios, comprendió que era allí donde debía comenzar a buscar a Michel Témoin. El templo, soberbio, era mucho más impresionante de lo que se había imaginado. Ninguna fotografía hacía justicia a aquel recinto de 7.700 metros cuadrados construidos, capaz de albergar a diez mil fieles para un solo oficio religioso. Monnerie, cautivado, descendió del Mercedes y se dirigió a buen paso hacia una de las puertas laterales del templo, justo aquella que pasa por debajo del gigante de piedra que representa a san Cristóbal. Atravesó su portezuela de madera y desembocó muy cerca de la nave central, junto al laberinto. Prácticamente vacía, los pocos turistas que en esos momentos aún se encontraban en el interior de la catedral disparaban apresuradamente sus flashes, tratando de no llamar la atención de los vigilantes. Meteor man echó un vistazo a su alrededor. Al principio no lo vio, pero una segunda «batida» a lo largo del muro norte le hizo sentir que allí había algo que no encajaba. Miró dos o tres veces más. No se trataba de ningún turista. Era algo del propio templo. En efecto, a unos metros por delante de él, en el crucero, el rosetón encastrado en la fachada norte presentaba un aspecto fuera de lo común. Tanto, que creyó que se trataba de un fenómeno óptico, de una confusión. El ingeniero dio unos pasos adelante para apreciarlo mejor, confirmando lo que se temía: los «nervios» del círculo central de su estructura... ¡formaban una estrella de cinco puntas invertida! ¡El símbolo medieval de Lucifer! No había duda. Se trataba de una estrella de cinco puntas invertida, la misma que tantas veces había visto asociada en películas y libros a la magia negra y al Diablo. Se estremeció. ¿Qué hacía aquel «sello» en un templo como aquél, tan visible? ¿Tendría razón monsieur Charpentier y, sin quererlo, estaría ahora implicado en una lucha de ángeles y demonios? Tratando de no perder la serenidad —con aquellas cosas, ciertamente era muy fácil—, Monnerie deambuló por las naves laterales del templo en busca de su «objetivo». Se detuvo ante la capilla de San Nicasio, justo detrás del altar mayor, donde admiró unas magníficas vidrieras en las que podía distinguirse un coro de reyes tañendo sus arpas. —La música —explicaba en ese momento un guía a su reducido grupo de turistas jubilados— era muy importante en la época de esplendor de las catedrales. Los templos se edificaban siguiendo la misma proporción matemática que Pitágoras aplicó a las cuerdas de los instrumentos musicales para que sonaran armónicamente. Ese saber, Pitágoras lo trajo de Egipto. «Egipto.» Meteor man se repitió mentalmente aquel nombre, mientras se alejaba del grupo rumbo a otra capilla, la de San Agustín de Cantorberry. Un cartel indicaba que su absidiolo había sido modificado por Napoleón III, pero que sus vidrieras eran originales. Del siglo XIII. Realmente eran brillantes. Cuadros con pequeñas escenas representaban personajes sumidos en actividades frenéticas. Una de ellas, la más nítida del conjunto, mostraba a dos individuos con mantos blancos transportando un cajón gracias a dos varas que atravesaban longitudinalmente sus costados. Más arriba, otras cuatro «viñetas» daban a entender que aquel cajón había llegado por mar y que los hombres de los mantos blancos se habían hecho cargo de él para llevarlo... ¿adónde? Monnerie tardó, pero cayó en la cuenta. ¡El Arca! Como si hubiera recibido una revelación divina, el profesor saltó sobre el pavimento de piedra. «Eso es exactamente lo que busca Témoin.» Un clérigo que salía en ese momento de la vecina sacristía pasó a su lado, mirándolo con incredulidad. Por supuesto, no desperdició la ocasión. —¿Otras representaciones del Arca de la Alianza, dice? —murmuró el anciano, mirándole con sus vivarachos ojos grises. El ingeniero jefe asintió. —Naturalmente, joven. Cada vidriera tiene su correspondencia en piedra, y ese arcón que usted ve en el lado interior este de la catedral, lo encontrará justo en su vertiente opuesta. —En la fachada exterior oeste. —Precisamente —sonrió—. La lástima es que no podrá verla usted muy bien. El Cabildo gasta casi todo su dinero en mantener limpio ese frontis, y estamos siempre de obras. No se imagina lo que el dióxido de carbono puede llegar a comerse la piedra. —¿Y no sabrá usted qué se ejecutó primero, si la vidriera o la fachada oeste? El clérigo sonrió de nuevo, como si la ignorancia de aquel nervioso visitante le produjera ternura. —¡Qué cosas tiene usted! —exclamó—. La cara oeste fue lo primero que se terminó de esta catedral. Déjeme pensar. Seguramente la levantaron los mismos que terminaron en 1220 la catedral de Chartres, así que debe de ser de 1230 o por ahí. Y por eso es la que más cuidados requiere. —¿De veras? La perilla puntiaguda de meteor man se arrugó bajo su labio inferior. Siempre que algo le impactaba hacía aquel gesto, mordiéndose la comisura de los labios con fruición mientras pensaba su siguiente paso. Así pues, excitado, tomó las manos fibrosas del clérigo y las sacudió enérgicamente, agradeciéndole sus servicios con un billete de cien francos. «Para la restauración», dijo poniéndolo entre sus dedos. El pobre no entendió mucho el porqué, pero aceptó aquel gesto extravagante. San Juan —pensó para sus adentros— atrae a muchos desorientados hasta allí, colocándolos en el verdadero camino de la fe. Afuera no había nadie. Al ser sábado, los obreros responsables de la limpieza de la fachada no estaban merodeando por allí, y los andamios, cubiertos por una tela plástica grisácea, parecían vacíos. La puerta del Arca debía de ser la de Notre Dame. Situada más a la derecha, se trataba de un pórtico ojival de profundidad media flanqueado por medallones que la estructura metálica de aquellas plataformas metálicas dejaban ver a duras penas. Sus relieves eran sorprendentes: hombres con gorros frigios parecían mirar planetas y estrellas, tomar medidas con sus manos, y levantar después torres sobre el suelo. «Como en el Picatrix.» La huida de José, María y el niño Jesús a Egipto a lomos de un burro, los tres Reyes Magos o el árbol del Paraíso, se mezclaban con medallones que representaban a Moisés frente a la columna de nubes que guió al pueblo elegido durante el Éxodo. Aunque Monnerie no era un experto en la Biblia, sabía que aquellas medallas se referían a pasajes muy diferentes y muy separados en el tiempo. En cierta manera, su común denominador —todos parecían pendientes del movimiento de ciertas estrellas grabadas en piedra— le recordó al amuleto de Catalina. Sin embargo, antes de que pudiera tomar nota de la posición de los astros, justo cuando pasaba sus manos por el relieve de un hombre con una vara mirando al cielo, una voz le gritó desde arriba. —¡No toque eso! —bramó—. ¡Es la vara de Aarón! Sorprendido, el ingeniero volvió la cabeza hacia allí. A unos cuatro metros de altura, por encima del parteluz con la estatua de la Virgen y el niño, un rostro regordete, muy rojo, le observaba fijamente. Y no era uno de los obreros. —¡Michel! —Meteor man lo identificó de inmediato—. Es usted... ¿verdad? La cabeza desapareció de inmediato, seguida por el brusco martilleo de unos pasos sobre los travesaños metálicos. Cuando cesaron, el pulcro bigote de Michel Témoin estaba a escasos centímetros de su rostro. —Por todos los diablos, profesor. ¿Qué hace usted aquí? —Eso debería preguntarle yo, ¿no cree? —Bueno —dudó—, estoy recogiendo datos para explicarle por qué el ERS se comportó de forma tan extraña hace unos días. Sigo cesado de mis funciones, ¿recuerda? —Desde luego. —Creí que mi secretaria le había informado de que salí de viaje. ¿Cómo me ha encontrado? —Es una larga historia, Témoin. —Por aquí también han pasado muchas cosas, ¿sabe? Pero creo que ya tengo respuesta para algunos interrogantes. Monnerie esperó a que su ingeniero recuperara el aliento de su rápido descenso, y le invitó a sentarse en la barandilla de piedra que tenían allí mismo. —En realidad, ya no necesito respuestas a lo del ERS, Michel —dijo el profesor sin esperar más—. Yo mismo retiraré el expediente que le abrí y pediré al gabinete de D’Orcet que olvide los cargos contra usted por negligencia. —Vaya. ¿Ha ocurrido algo que deba saber? —Hablé con la Fundación Charpentier, como usted me sugirió, y a ellos no les sorprendieron los resultados del ERS. —¿Charpentier? —su rostro mudó de repente, al recordar las últimas palabras de Letizia antes de ser secuestrada—. Debo hablar con la Fundación de inmediato. —Aguarde un momento. Déjeme explicarle algo antes. —Usted no lo entiende, profesor. —Sí lo entiendo. De alguna manera, la Fundación ha estado al corriente de todas sus actividades durante este tiempo. Ellos sabían que estaba aquí y me han mandado para que hable con usted. Temen que su investigación sobre las «anomalías» en las catedrales sea aprovechada por terceros para apropiarse de algo indebido. La palabra «indebido» molestó a Témoin. —¿Indebido? ¿Le parece indebido que hayan secuestrado a Letizia? —gritó —. ¿Se acuerda de Letizia? ¿Eh? ¿Se acuerda? Las protestas de Témoin retumbaron bajo el pórtico de Notre Dame. Su interlocutor, impasible, ni siquiera se inmutó por aquella revelación. —Eso también lo saben, Michel. De hecho, ya la están buscando por su cuenta, y la encontrarán, amigo mío. —¿Cómo? —Letizia es una de los suyos. —¿De los suyos? ¿Qué quiere decir? La ira del ingeniero se transformó de repente en curiosidad. —Que trabajaba para la Fundación y que el contacto que usted estableció con ella entraba dentro de sus planes. Eso me dijeron. Por cierto, que la relación que usted estableció entre aquel Louis Charpentier de donde sacó su idea de la «conexión estelar» de las catedrales y la Fundación de ese nombre, debe de ser cierta. Son una especie de sociedad secreta. —Esta bien —dijo sin importarle demasiado el último comentario del profesor— Supongamos que la encuentran. Lo que no me explico es por qué le envían a usted a detenerme. —Accidentalmente, el CNES se ha visto envuelto en algo que no le incumbe. Y si el cliente que nos ha metido en este embrollo dice que paremos, debemos hacerlo. Sólo le diré una cosa más, monsieur Charpentier me mostró en París un amuleto antiguo en el que la situación de sus estrellas parece coincidir con la ubicación actual de la bóveda celeste sobre Francia. Me explicó que era una especie de aviso profético de que en estos días algo se activaría en estos templos. Es decir, ellos sabían lo que iba a pasar. —¿Algo? ¿Que se va activar7 —Algo relacionado con las catedrales. Un supertalismán o algo así que forma parte de una Puerta. La verdad es que no entendí muy bien el galimatías que me contó, aunque me dejó incluso un libro para que lo estudiara. —¿Le habló de una Puerta? Letizia me dijo que las catedrales eran como Puertas Estelares. —¿Y la creyó? Ni los cristales de las gafas de pasta negra de Temom amortiguaron el fuego de su mirada. —Sí. La verdad es que sí. —Está en su derecho, naturalmente, pero... —Dígame, ¿le dijo monsieur Charpentier algo acerca del Arca de la Alianza? Monnerie dejó pasar un par de segundos antes de responder. —Sí. Que fuera lo que fuese su contenido, allí se encontraba el origen de las emisiones que captó nuestro satélite. Creo que lo llamo la «fuente». —¡Exacto! Y lo que contiene el Arca, según me explicó Letizia, son los Libros Esmeralda de Hermes. —A Hermes también lo citó, en efecto. —Profesor, somos dos peones accidentales en un tablero del que no conocemos nada. Y si no somos capaces de desvelar ahora de que va todo esto, nos vamos a quedar con la duda el resto de nuestras vidas. Yo no sé —continuó— que demonios son los Libros de Hermes ni que contienen, pero si sé que ocultan una especie de pila energética. Y es tan fuerte que es nuestra responsabilidad destaparla y ponerla bajo control científico. Imagine si otros menos preparados dan con ella por azar... ¡sería un desastre! Meteor man dudó. —¿Y dónde cree usted que se esconde esa pila? —En el Arca, naturalmente. ¿Aún no la vio? Témoin, risueño, señaló a través de los andamios un bulto rectangular ubicado justo sobre la corona de la Virgen. Se trataba de una caja de buen tamaño, idéntica a la que él mismo tocó en el pórtico norte de Chartres, y tallada con sus mismos cerrojos de piedra. La flanqueaban varias estatuas sedentes de los principales patriarcas del Antiguo Testamento. Allí estaba Jacob —el de la Scala Dei—, Abraham —el que protegió la Roca del Monte Moriah—, Salomón —custodio del Arca en su Templo—, David... El Arca de Amiens estaba allí, a la vista de todos. Monnerie, absorto, se quedó contemplándola un buen rato antes de decir nada. Era el mismo cofre que había visto en las vidrieras de la capilla de San Agustín de Cantorberry. Exactamente el mismo, pero de piedra. Cuando se convenció de lo que veían sus ojos, temblando, propuso algo que nunca antes hubiera imaginado hacer. —¿La... abrimos? —susurró. —Claro, profesor. El poderoso micrófono direccional Siemmens instalado en el techo de la Renault Space captó a la perfección las últimas palabras de Michel Témoin. —Esto ha llegado demasiado lejos —dijo Gloria con los ojos desorbitados —. Os dije que no se detendría por que retuviéramos a su ayudante. Tiene un perfil de personalidad que le hace demasiado obstinado. Gérard y Ricard no replicaron, y el padre Rogelio, extrañamente sereno, dejó hacer a la impetuosa jovencita. —Si no hacemos algo, ¡los Libros de Hermes terminarán en sus manos! ¡Y la Puerta será suya! —Quizá —dijo parco el ortodoxo, mirando fijamente el pórtico sur de Amiens y las siluetas de Monnerie y Témoin dirigiéndose hacia el andamio. —Pero ¡padre! —Quizá todo esto forme parte del Plan de Dios. De la señal que espera el padre Teodoro en el Sinaí. —Señal, ¿qué señal? —bufó Gloria. El ortodoxo no respondió. https://groups.google.com/group/secreto-masonico/browse_thread/thread/89f7608e20093ef5/656d61142a909bff?lnk=gst&q=egipto#656d61142a909bff |
|
|
|
|
La Masonería se sirve de diferentes símbolos y emblemas para el uso exclusivo y reservado de sus miembros, que se transmiten por tradición desde tiempos inmemoriales, y cuyo secreto significado o interpretación sólo puede ser explicado a través de años de dedicación en constante estudio masónico. Estos símbolos y emblemas constituyen una lenguaje secreto, sumamente indescifrable para el profano, pero para el masón son claros y sirven para que los masones se entiendan entre sí, en todas las circunstancias de la vida, cualquiera sea su idioma en cualquier parte del mundo en que se encuentren, pudiendo así disfrutar de las inapreciables ventajas de comprensión que les otorga la institución. Es exactamente como una Torre de Babel pero a al inversa, todos comprendemos entre sí en una mismo lenguaje de símbolos. El carácter para unificar criterios en base a la institución a base de símbolos y emblemas, toques y palabras, impone a todos los masones el deber de respetarlos, mantenerlos y transmitirlos íntegramente tal como se hallan contenidos en las liturgias de los tres grados, liturgias admitidas, revisadas y sancionadas por maestros masones y por las antiquísimas y tradicionales prácticas que nos han sido legadas por nuestros antepasados masones- El simbolo de la Torre de Babel; es la confusión, según se nos presenta en la Biblia. La idea en torno a la cual está relacionando en un relato en la que el hombre quiso alcanzar un nivel superior de desarrollo haciendo uso de su saber profano. Este es el significado de una construcción hecha a capricho por el hombre. Pero lo que lo que nos dice puede comprenderse que el logro de un nivel muy superior requiere que se siga una enseñanza no profana, y que con ningún conocimiento meramente profano, puede considerarse digno para construir un edificio del orden espiritual. No podemos desarrollarnos espiritualmente mediante nuestras propias ideas . Tenemos que someternos a una enseñanza superior en este caso la masonería. Nuestros conocimientos deben cimentarse en una Verdad – sólida – en este caso la Fraternidad, la Igualdad, la Libertad y la Tolerancia, cosas fuera de estos conceptos ya sean países o individuos estarán mal cimentadas y caerán. Y este conocimiento o Verdad. Le podemos llamar piedra, la torre de Babel estaba construida de barro cocido, se dice que la humanidad hablaba una sola lengua y un solo lenguaje y que tras la caída de la Torre produjo la confusión de lenguas. Si tenemos idea que tenian ladrillos, ladrillos es un matrial hecho por manos humanas, en lugar de piedras solidas hechas por la Naturaleza. El Fenómeno Masónico es: El lugar dónde todos volbemos a comprendernos entre sí, mediante un lenguaje simbólico iniciático, contrario a lo que sucedió en la Torre de Babel |
|
|
|
|
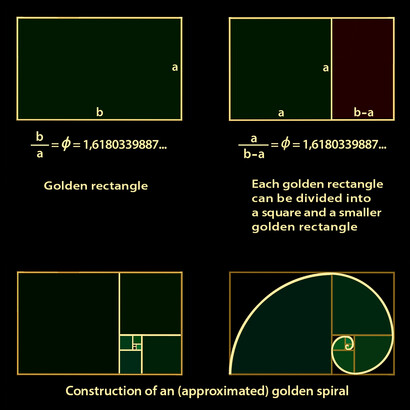
The amount of days in a solar year plus the proportions for the Equatorial circumference of the Earth and the proportions of the Great Pyramid of Giza according to Golden Pi = 4/√φ = 3.144605511029693144: The Great Pyramid of Giza is a geodetic model of Planet Earth. The measurements mentioned below are the ideal measurements. A meter is equal to 100 centimeters 1 Solon cubit = 40 times √φ = 50.88078598056276 centimeters. If 1 Solon cubit is divided into 20 equal units of measure then 20 inches can be derived because 1 Solon cubit is equal to 20 inches. 1 Saylen cubit = 50 times √φ = 63.60098247570345 centimeters. If 1 Saylen cubit is divided into 25 equal units of measure then 25 inches can be derived because 1 Saylen cubit is equal to 25 inches. 1 inch = 2 times √φ = 2.544039299028138 centimeters. 1 foot = 12 inches. 1 foot = 24 times √φ = 30.528471588337656 centimeters. If the shortest edge length of a Kepler right triangle is equal to 1 then the hypotenuse of the Kepelr right triangle is equal to The Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 according to the Pythagorean theorem. The Golden ratio in Trigonometry = (cosine (36 degrees) times 2) = 1.618033988749895. If the shortest edge length of a Kepler right triangle is equal to 1 then second longest edge length of the Kepelr right triangle is the square root of the Golden ratio = √φ = 1.272019649514069 according to the Pythagorean theorem. The width for the square base of the Great Pyramid of Giza is equal to 756 feet. • If the shortest edge length of a Kepler right triangle is equal to 1 foot and then the second edge length of the Kepler right triangle is multiplied 378 equal times the result will be the height of the Great Pyramid of Giza = 378 times √φ = 480.823427516318082 feet according to Golden Pi = 4/√φ = 3.144605511029693144. • If the shortest edge length of a Kepler right triangle is equal to 1 foot and then the hypotenuse of the Kepler right triangle is multiplied 378 equal times the result will be the slant height of the Great Pyramid of Giza = 378 times φ = 611.61684774746031 feet according to Golden Pi = 4/√φ = 3.144605511029693144. • If the shorter edge length of a Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 rectangle is equal to 1 foot and then the diagonal of the Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 rectangle is multiplied 378 equal times the result will be the edge height of the Great Pyramid of Giza = 378 times = Cosine (18) degrees times 2 = 1.902113032590307 = 718.998726319136046 feet according to Golden Pi = 4/√φ = 3.144605511029693144.Cosine (18) degrees times 2 = 1.902113032590307. Cosine (18) degrees times 2 = 1.902113032590307 squared = φ plus 2 = 3.618033988749895. • If the shortest edge length of a Kepler right triangle is equal to 1 foot = 24 times √φ = 30.528471588337656 centimeters then the second longest edge length of that Kepler right triangle is equal to 38.832815729997479 centimeters.24 times √φ = 30.528471588337656 centimeters times the square root of the Golden ratio = √φ = 1.272019649514069 = 38.832815729997479 centimeters. 1 foot = 24 times √φ = 30.528471588337656 centimeters times the square root of the Golden ratio = √φ = 1.272019649514069 = 38.832815729997479 centimeters times 378 = the height of the Great Pyramid of Giza of Giza = 14678.804345939047062 centimeters. The height of the Great Pyramid of Giza = 14678.804345939047062 centimeters divided by 24 times √φ = 30.528471588337656 centimeters = the height of the Great Pyramid of Giza = 480.823427516318088 feet. 378 times √φ = 1.272019649514069 = 480.823427516318088. • If the shortest edge length of a Kepler right triangle is equal to 1 foot = 24 times √φ = 30.528471588337656 centimeters then the hypotenuse of that Kepler right triangle is equal to 49.39610465451582 centimeters. 24 times √φ = 30.528471588337656 centimeters times the Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 = 49.39610465451582 centimeters. 1 foot = 24 times √φ = 30.528471588337656 centimeters times the Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 378 = 49.39610465451582 centimeters times 378 = slant the height of the Great Pyramid of Giza = 18671.727559406979971centimeters. The Slant height of the Great Pyramid = 18671.727559406979971 centimeters divided by 24 times √φ = 30.528471588337656 centimeters = the slant height of the Great Pyramid of Giza = 611.61684774746031 feet. 378 times √φ = 1.272019649514069 = 611.61684774746031. • If the shortest edge length of a Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 rectangle is equal to 1 foot = 24 times √φ = 30.528471588337656 centimeters then the length of the diagonal of that Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 rectangle is equal to 58.068603673239965 centimeters. 24 times √φ = 30.528471588337656 centimeters times Cosine (18) degrees times 2 = 1.902113032590307 = 58.068603673239965 centimeters. Cosine (18) degrees times 2 = 1.902113032590307 squared = φ plus 2 = 3.618033988749895. 1 foot = 24 times √φ = 30.528471588337656 centimeters times = Cosine (18) degrees times 2 = 1.902113032590307 = 58.068603673239965 centimeters times 378 = the edge height of the Great Pyramid of Giza of Giza = 21949.932188484706835 centimeters. The edge height of the Great Pyramid = 21949.932188484706835 centimeters divided by 24 times √φ = 30.528471588337656 centimeters = the edge height of the Great Pyramid of Giza = 718.998726319136046 feet. 378 times Cosine (18) degrees times 2 = 1.902113032590307 = 718.998726319136046. Cosine (18) degrees times 2 = 1.902113032590307. Cosine (18) degrees times 2 = 1.902113032590307 squared = φ plus 2 = 3.618033988749895. A Kepler right triangle can be created from the construction of a Golden ratio = (√(5) plus 1)/2 = φ = 1.618033988749895 rectangle by using Compass and straight edge and obviously a marker for the drawing surface. The amount of days in a Solar year = 4/√φ times 7920 times 5280/(10 ^ 3 times 360) = 365.277376161209156. The amount of days in a Solar year = 4/√φ = 3.144605511029693144 times 7920 times 5280/(10 ^ 3 times 360) = 365.277376161209156. The equatorial circumference of planet Earth = 10 ^ 3 times 360 times 365.277376161209156 = 131499855.41803529616 feet. The equatorial circumference of planet Earth = 4/√φ = 3.144605511029693144 times 7920 = 24905.275647355169727 statute miles. 131499855.41803529616 feet divided by 86400 = half the perimeter of the socle of the Great Pyramid of Giza = 1521.989067338371483 feet. Half the perimeter of the socle of the Great Pyramid of Giza times 86400 is also equal to the equatorial circumference of planet Earth = 131499855.41803529616 feet. 484 divided by √φ times 2 = the width of the socle of the Great Pyramid of Giza = 760.99453366918572 feet. Half the width of the socle of the Great Pyramid of Giza = 380.49726683459286 feet times √φ = 484 feet. 484/√φ times 2 times 2 times 86400 = 131499855.41803529616 feet. 131499855.41803529616 feet divided by 5280 = The perimeter of the socle of the Great Pyramid of Giza = 484/√φ times 8 = 3043.978134676742966 feet. 484 feet /√φ times 8 = 3043.978134676742966 feet times 12 = 24905.275647355169727 statute miles. 24905.275647355169727 statute miles divided by 7920 statute miles = Golden Pi = 4/√φ = 3.144605511029693144. There are 929.28 meters in the square perimeter of the socle of the Great Pyramid of Giza according to Golden Pi = 4/√φ = 3.144605511029693144. 484/√φ times 8 = 3043.978134676742966 times 12 = 36527.737616120915592 divided by 100 = the exact amount of days in a solar year = 365.277376161209156. The equatorial diameter of our planet Earth = 41817600 feet. 41817600 feet divided 86400 = the height of the Great Pyramid of Giza = 378 times √φ = 480.823427516318082 feet plus the height of the socle of the Great Pyramid of Giza = 3.176572483681918 feet. 10 ^ 3 times 360 times 484/(√φ) times 8 times 12/(100) = 131499855.41803529616 feet. The height of the Great Pyramid if Giza is 378 times √φ = 480.823427516318082 feet. The width of the square base of the Great Pyramid of Giza is 756 feet. The perimeter of the square base of the Great Pyramid of Giza = 3024 feet. 9 factorial = 362880. At 10 degrees latitude the length of a degree is 9 factorial =362880 feet. The amount of inches in the perimeter of the square of the Great Pyramid of Giza = 36288. 36288 times 10 = 362880. The width for the square base of the Great Pyramid of Giza = 756 feet. The perimeter of the square base of the Great Pyramid of Giza = 3024 feet. There are 36288 inches in the perimeter of the square base of the Great Pyramid of Giza. 3024 times 12 = 36288. 756 times 4 times 12 = 36288. (9!)/10 = 36288. The equatorial circumference of planet Earth: https://joedubs.com/four-earthly-elements/equatorial-circumference-of-earth/ Kepler right triangle diagram with squares upon the edges of the Kepler right triangle: https://drive.google.com/file/d/1iBtXYy06yv9UWtGP5mwMXyt80vaysFvR/view?usp=sharing Kepler right triangle construction method: https://drive.google.com/file/d/15DNXB_xNP2f2jCroC0FyNUyBYGhVAA2J/view?usp=sharing PYTHAGOREAN THEOREM: https://en.wikipedia.org/wiki/Pythagorean_theorem Golden ratio: https://en.wikipedia.org/wiki/Golden_ratio The history of the meter: The history of the meter: https://www.factinate.com/editorial/meter-history/ The meter: https://en.wikipedia.org/wiki/Metre The meter is based now on the speed of light: https://www.youtube.com/watch?v=vgqUyFaUDcI
|
|
|
|
|
|
|
|
|
De: Kadyr |
Enviado: 20/06/2024 01:56 |
|
|
|
|
According to Pythagoras an entity is called a number when the product of itself is greater than the sum of itself. One is not a number, according to the above definition, it is god, generator of numbers. Two is also not a number, because both the product and the sum are equal to each other, that is, it is a coexisting god, a second generator of numbers. The numbers start with three because 3 X 3 = 9 an

The Tetraktys is the Essence of Teaching and the Sacred Symbol of the Pythagoreans. It consists of the first ten numbers (1-10) arranged in four rows (one in the first row, two in the second, three in the third and four in the fourth row) as shown in the picture. Tetraktyn was called “Tetradas”[1] which in Pythagorean Philosophy is the essence and meaning of the number four. Tetraktys is the fourth “triangular number”[2] thus showing another view of the relationship of Tetrad and Tetraktyos. In any case, we should not forget the relation of Tetraktys with “Ten”. From this the Tetraktys is mentioned according to Iamblichus with the prepositional names: Cosmos (decoration, ornament), Pan (the god Panas – Pan = All), Uranus, Atlas, Key, Aion, Memory, Gnomon, Eimarmene, Kratos, Phanis, Helios, Pythmen et al. By studying the concepts of numbers found in the Tetractyn and their relationships, the Pythagoreans argue that one reaches the attainment of wisdom.
The main relationship of Tetrad and Tetraktyos can also be seen from the famous relationship of the first four numbers with the ten they produce when added (1+2+3+4=10). From these first four numbers (1, 2, 3 & 4), it is possible to construct the ratios: “by four” (4:3, fourth), “by five” (3:2, fifth), “by all ” (2:1, Octave), which attribute to music the mentioned harmonic musical intervals which Pythagoras was the first to precisely determine with numerical reasons. These proportions create Harmony, which for the Pythagoreans has a literally cosmic meaning (hence its name “Cosmos”). The Pythagoreans used the Tetraktyn to swear, even invoking Pythagoras as a god, as can be seen from the “Golden Epics” where it is stated:
“Yes, with the immortal soul, delivered four times
always of a permanent nature.”
(yes, but the one who delivered to our soul the tetractyn,
which is the source of eternal nature.)
Numbers are related to geometric shapes. Thus the unit is related to the point, the dyad to the line, the triad to the triangle, and the tetrad or tetraktys to the tetrahedron (or triangular pyramid), the first geometric solid. Its symbol was considered the square which was also the symbol of the divine and perfection.[5]. Also wisdom was considered to be acquired from the four esoteric sciences for the Pythagoreans of arithmetic, music, geometry and astronomy. It is a symbol of God Apollo and the Pythagoreans connect the Tetraktyn with the Oracle of Delphi, as seen in the important “hearing” about existence mentioned by Iamblichus[6]: “what is the Oracle in Delphi? Tetraktys” (what is the Oracle of Delphi? Tetraktys).
There is another Tetraktys, as mentioned in Plato’s Timaeus, which is called a double Tetraktys and consists of eight lines created by the first eight numbers (1, 2, 3, 4, 5, 6, 7, which in total give a total of 36 (1+2+3+4+5+6+7+8=36). From another point of view this Quadrilateral is created, and thus connected to the regular Quadrilateral Quadrilateral, by the sum of the first four odd numbers and of the first four integers: (1+3+5+7)+(2+4+6+8)=36 as mentioned by Plutarch in “On Isis and Osiris”.
GOLDEN RATIO Φ ON THE PYTHAGORIAN SYMBOL
PARTHENON WAS BUILT on the PRNICIPLES of PYTHAGORAS
 
The FIRST FLYING MASCHINE was BUILT by the GREEK PYTHAGOEIAN PHILOSOPHER ARCHYTAS in TARANTO(CORINTHIAN COLONY) SOUTHERN ITALY.
For the Pythagoreans, a politician was the person who, after having been taught philosophy, returned to the world to be useful to others.
He is not interested in positions and powers but in the improvement of society.
The one who chose to become a politician could not pass to the stage of a mathematician, that is, one who can deliver lessons and teach.
Those who could had the advantage of living near Pythagoras.
Friendship and companionship were of the highest importance for the Pythagoreans and they considered that universal love was reflected in these two elements.
They were bound by an oath of secrecy over the higher teaching, the ceremonies and the sacred symbols.
Pythagoras offered mankind a universal “successful experiment” for this and later Plato would call education with music and gymnastics!!!!

ONE OF THE BASIC PYTHAGORIAN GROUNDS FOR: ARCHITECTURE, GEOMETRY, MUSIC, STEREOMETRY, ASTRONOMY, HARMONY AND PHILOSOPPHY

WHAT DID PYTHAGORAS SAYABOUT WOMAN=ΓΥΝΗ/GYNE
https://euphoriatric.com/pythagoras-the-nine-muses/ |
|
|
|
|
Freemasonry works with a system of degrees, which represent stages of personal development. There are different systems in use in the various rites of freemasonry, such as the York Rite, Ancient and Accepted Scottish Rite, Rectified Scottish Rite, Modern French Rite, and Mexican Rite, etc. ... . The number of degrees ranges from 7 degrees in the York Rite and the Modern French Rite, 33 in the Ancient and Accepted Scottish Rite and even 100 degrees in the Rite of Memphis-Misraim. The concept of 33 degrees or a 33-fold classification system seems widespread in Indo-European and Semitic culture. Both an Indo-European and Semitic intepretation is possible. The 33 degrees of the Scottish Rite are equal to the years of life of Jesus of Nazareth (7-2 BCE to 30-33 CE) in the Bible of Christianity and Jesus performed 33 recorded miracles. This came to represent the highest meaning of the number '33', which is that it represents the highest spiritual consciousness to which man can attain. In the Old Testament in 1 Chronicles 29:26-27 we find "Now David the son of Jesse reigned over all Israel. The period which he reigned over Israel was forty years; he reigned in Hebron seven years and in Jerusalem thirty-three years". The Kabalistic Tree of Life (עץ החיים) contains 33 permutations of consciousness - 22 paths, 10 known/drawn sephiroth (סְפִירוֹת), and an 11th hidden sephiroth left undrawn in most renditions. Da'ath, the 11th, is the hidden secret of the void, or the abyss. Da'ath as such is not a sephirah, but rather is all ten sephirot united as one. Da'ath relates to the Divine Light which is always shining, but not all humans can see it. Without Da'ath there are only 10 sephiroth drawn and only 32 permutations of consciousness. The number 33 also plays a role in Greek mathematical philosophy such as with Pythagoras (ca. 570-ca. 490 BCE) and Plato (424/423-348/347 BCE). The Pythagoreans evolved their philosophy from the science of numbers. For Pythagoras 33 was the most important of the master numbers (11, 22, 33, 44) Some sources say that there were 33 Egyptian mysteries (see Churchward, 1913). Christian Gnostics taught that the emanations from the Deity were all summed up in one absolute Unity, 33 in all (see G.R.S. Mead, 1908). According to the Persian Muslim scholar Al-Ghazali (ca. 1058-1111 CE) the dwellers of Heaven will exist eternally in a state of being age 33. Islamic misbaḥah (prayer beads) are generally arranged in sets of 33 in order to keep track in Tasbih, which involves the repetitive utterances of short sentences glorifying Allah. In the Vedic Religion there are thirty-three gods or Tridasha. Tridasha generally includes a set of 31 deities consisting of 12 Ādityas, 11 Rudras, and 8 Vasus. The identity of the other two deities that fill out the 33 varies. In the Tibetan Book of the Dead, it speaks of the thirty-three heavens ruled over by Indra and the thirty-three ruled over by Mara. There is also the legend of the meaning of the 33rd Parallel, which is popular in conspiracy theories on freemasonry. Another set of myths connects the human vertebral column and freemasonry with the Tree of Life and the Biblical Tree of the knowledge of good and evil (עֵץ הַדַּעַת טוֹב וָרָע) and the serpent in the Biblical Garden of Eden. A normal human spine has 33 vertebrae when the bones that form the coccyx are counted individually. The 33 vertebrae and the 33 degrees of freemasonry can be linked to the symbol of the serpent in the Biblical Garden of Eden (Gen 3:1-20) and the fall of man as follows (FWIW). In ancient Kundalini Yoga, the Kundalini serpent-energy is said to rise from the root chakra, coiling up and around the spine until illuminating the crown chakra of spiritual enlightenment. Inside the Kabalistic Tree of Life in some myths there resides a sacred serpent which somehow connects Kabbalah to Kundalini Yoga. A Tree of Life is often related to physical life and the serpent to the added meaning of spiritual life. In Greek mythology we also find some serpents entwining a rod or tree. The winged messenger (nuntium volucrem) Hermes, the Greek god of transitions and boundaries, carries the caduceus (κηρύκειον). The caduceus is a short staff entwined by two serpents, sometimes surmounted by wings. Hermes is related to the myth of Hermes Trismegistus and Hermeticism. There is also the Staff of Asclepius a (single) serpent-entwined rod wielded by the god Asklēpiós, a Greek associated with healing and medicine. The story of the (ascending) serpent is sometimes linked to the myth of the garden of Atlas, who had seven (or 4) daughters called the Hesperides (seven daughters linked to the 7 chakras) who guard the Tree of Life (cfr. spinal column) and its golden apples of immortality. They were assisted by a serpent-like dragon called Ladon entwined around the three. The myth of the Garden of the Hesperides is then linked to the myth of Atlantis which links freemasonry to the myths and secrets of Atlantis and the Atlantean conspiracy. This serpentine labyrinth of myths and an example of syncretism is believed to link the serpent in the Garden of Eden (Genesis 3) to the 33 (vertebral) degrees of freemasonry. Logic is powerless when the 'principia neutra' or first principles are wrong from the start, because 'Contra principia negantem non est disputandum' (see also The Lost Language of Symbolism, Harold Bayley, Dover Publications, 2006, p. 364 The Signs and Symbols of Primordial Man, Albert Churchward, G. Allen & Company, 1913, p. 117, 177 and The Wedding-song of Wisdom, George Robert Stow Mead, Theosophical Publishing Society, 1908, p. 36 and The Kabbalah Tree: A Journey of Balance & Growth, Rachel Pollack, Llewellyn Worldwide, 2004, p. 8 and The Tibetan Book of the Dead: Or The After-Death Experiences on the Bardo Plane, W. Y. Evans-Wentz, Oxford University Press, 2000, p. xxxvii and The Secret Doctrine: The Synthesis of Science, Religion and Philosophy, Volume 1, Helena Petrovna Blavatsky, Theosophical University Press, 1963, p. 93 and The Green Serpent and the Tree: Kabbala and Kundalini Yoga, James N. Judd, MS.D.,D.D., Xlibris Corporation, 1999, p. 107 and An Essay on the mythological significance of Tree and Serpent Worship, etc., Thomas Scott, 1870, p. 19 and The Nature of the Archons: A Study in the Soteriology of a Gnostic Treatise from Nag Hammadi (CGII, 4), Ingvild Sælid Gilhus, Otto Harrassowitz Verlag, 1985, p. 66 and Atlantis in Wisconsin: New Revelations about the Lost Sunken City, Frank Joseph, Galde Press, Inc., 1995, p. 52 and The Atlantean Conspiracy (Final Edition), Eric Dubay, Lulu.com, 2013, p. 195 and Masonic rituals and degrees and Entered Apprentice Ritual - Emulation and Fellow Craft Ritual - Emulation and Master Mason Ritual - Emulation and Ancient and Accepted Scottish Rite (AASR) and Cérémonie d'Initiation - Rite Français and Cérémonie de Passage - Rite Français and Cérémonie d'Elévation - Rite Français)
In the field of Numerology, many systems hold 33 as the highest of the "Master Numbers." It symbolizes "Christ Consciousness", or the ultimate attainment of consciousness or perfection (see also the Allegory of the Platonic Cave). Numerology reduces all multi-digit numbers to the single-digit numbers 1 through 9 with the exception of the three Master numbers 11, 22 and 33. Master Numbers are digits that are not "reduced" in some numerological traditions, such as 11, 22 and 33 (33 is not reduced to a "6", as is 42, for example). The number 11 represents the vision, while the number 22 combines vision with action and the number 33 offers guidance to the world. The essence of 33 in numerology is the final word in spiritual evolution; the 'Master Teacher'. Numerological 33 is characterized by a highly developed internal ethics and life should be marked by working for humanity. The Master Numbers 11, 22, and 33 are also believed to represent a triangle, a triangle of Enlightenment. The number 33 is the largest positive integer that cannot be expressed as a sum of different triangular numbers. The others are 2, 5, 8, 12, and 23. The number 33is also the smallest odd repdigit (natural number composed of repeated instances of the same digit) that is not a prime number (see also Numerology: The Power in Numbers, Ruth Drayer, Square One Publishers, Inc., 2003, p. 92).
Reaching the highest degree in freemasonry, means reaching "excellentia" or "perfectio", thereby comprising the paradox of perfection-that imperfection is perfect. The oldest definition of what is "perfection", goes back to Aristotle (384 BC-322 BCE) (Book Delta of the Metaphysics). Also in Aristotle's astronomy, presented in his Metaphysics, Physics and De Caelo (On the Heavens), there were 33 celestial spheres and he thereby followed Callippus (ca. 370-ca. 300 BCE) who had postulated 33 celestial spheres in all, 4 each for Saturn and Jupiter, 5 each for Mars, Venus, Mercury, the Sun and the Moon (see also Cosmology: The Science of the Universe, Edward Harrison, Cambridge University Press, 2000, p. 31).
Each symbolic degree is enacted within a masonic temple and a specific ritual which reminds of the classical Ars Memorativa (E: Art of Memory) (see also "Enactment theory" in Sensemaking in organizations, K. E. Weick, Sage, 1995). The "Ars Memorativa" was a specific technique for memorizing things, which has its origins in Greece. Originally, the intent of the art of memory was to greatly increase the natural capacity of the human memory. The practitioners of the art of memory tried to find ways of retaining, retrieving and using vast amounts of information. In late Medieval and Renaissance times, the art of memory gradually became highly symbolic. Neoplatonists and Hermeticists gradually adapted it to develop it into a special way of knowing, a special way of relating to the universe. Renaissance Hermeticists reasoned that if human memory could be reorganized in the image of the universe, memory became a reflection of the entire realm of Platonic Ideas, and therefore the key to universal knowledge. The microcosm of the memory would reflect the macrocosm of the universe. Images placed in a building need not be used to associate and recall arbitrary external ideas. The images might themselves be used to remind the observer of certain ideas. The emphasis shifted from the expansion of memory to the search for a universal language of symbols. The memory temple for them not only was a method for remembering speeches, but a tool for teaching. A masonic temple can be seen as a building specifically to be used for the art of memory, to embody all human knowledge. In this view each Lodge is, in fact, a Memory Temple, designed to elicit specific effects through the recollection of its images and symbols and physical motions as freemasons proceed through the Lodge (see also Ars Memorativa: An Introduction to the Hermetic Art of Memory, John Michael Greer, Caduceus and The Art of Memory, Frances A. Yates, University Of Chicago Press, 2001 and The art of memory and masonry, Clarence A. Anderson).
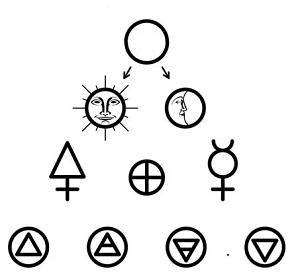
- The Pythagorean Tetractys -
Top row: The One
Second row: Sun and moon
Third row: Sulphur, salt, mercury
Bottom row: Fire, air, earth, water
These 33 degrees are divided to seven classes (Scottish Rite). The first class (Blue Lodges) comprises the three traditional symbolic or craft degrees: Entered Apprentice, Fellow-Craft, and Master Mason. Both the first and the third degree use the concept of spiritual death and resurrection. The first degree of 'Entered Apprentice' can be seen as the transition from the bottom row of the Pythagorean Tetractys to the second level, where man has to liberate hiself from his material or wordly chains. The second degree of 'Fellow-Craft' symbolizes the transition from the second level to the third level and the third degree of 'Master Mason' symbolizes the final step towards union with the Seelenfünklein or 'scintilla animae' within man. The concept of developing higher consciousness (e.g. Fichte's 'höhere Bewusstsein') can also be found in German Idealism and is "the part of the human being that is capable of transcending animal instincts" (see also Scintilla animae, Hans Hof, Gleerup, 1952 and Scintilla Animae: Eine Studie zu einem Grundbegriff in Meister Eckharts Philosophie mit besonderer Berücksichtigung des Verhältnisses der Eckhartschen Philosophie zur neuplatonischen und thomistischen Anschauung by Hans Hof, Kurt F. Reinhardt, Speculum, Vol. 30, No. 3 (Jul., 1955), pp. 474-476 and The Cambridge Companion to German Idealism, Karl Ameriks, Cambridge University Press, 2000, p. 263).
The ascent of a Freemason through the various degrees can be considered a spiritual or mystical journey. In mystical traditions a distinction is being made between theistic experiences, which are purportedly of God, and non-theistic ones. Theistic experience can be found in Hinduism, Sufism, Kabbalah, Christian mysticism and Pantheism, etc. ... . Non-theistic mysticism can be found in Taoism, Buddhism and secular or atheist mysticism. A few liberal Christian theologians, define a "nontheistic God" as "the ground of all being" rather than as a personal divine being. Non-theistic experiences can be allegedly of an ultimate reality other than God or of no reality at all. Spiritual Atheists believe that the entire universe is, in some way, connected; even if only by the mysterious flow of cause and effect at every scale (see also Mysticism in the World's Religions, Geoffrey Parrinder, Oneworld Publications, 1995 and Atheïstische spiritualiteit, Leo Apostel, VUBPress, 1998 and The Book of Atheist Spirituality, Andre Comte-Sponville, Random House, 2010 and Synchronicity: Nature and Psyche in an Interconnected Universe, Joseph Cambray, Texas A&M University Press, 2009, p. 24 and Synchronicity, Science and Soul-Making: Understanding Jungian Synchronicity Through Physics, Buddhism, and Philosophy, Victor Mansfield, Open Court Publishing, 1995, p. 77 and A New Christianity for a New World: Why Traditional Faith is Dying & How a New Faith is Being Born, John Shelby Spong, HarperOne, 2002).
Theistic mystical traditions speak about the 'journey in God' - of the intense longing for God and devotion of the soul to God - of surrender and purification, of renunciation and abandonment resolved through the union in Love. It has been said that all mystics recognize one another because they come from the same country. Yet behind the multiplicity of religious forms, ideas and expressions of that journey, there is but one 'God' and but one 'journey in God'. In Vedic-Hindu metaphysics this stage would symbolize the mystical union between Atman ~ being the "Self" ~ and Brahman ~ being the "World Soul". Some Buddhist traditions refer to Nirvana, while other refer to an experience of "unconstructed awareness" involving an awareness of the world on an absolutely or relatively non- conceptual level. The Mystical Union is also prevalent in Sufism, the mystical strain in Islam. Sufism developed religious practices focusing on strict self-control that enable both psychological and mystical insights as well as a loss of self, with the ultimate goal of mystical union with God. In the Sufi book Nawadir, a compilation of stories and religious thoughts attributed to Ahmad al-Qalyubi, there are seven castles, each one inside the other. In this text, the soul which aspires to contemplation is conceived as moving or evolving through seven degrees of perfection, which are like concentric castles of mansions, and in the seventh and innermost lives God where ecstatic union is achieved. The ecstatic tradition of Jewish Kabbalah strives to achieve a mystical union with God. In Kabbalah the mystic goes through seven heavenly halls act as a kind of bridge between the forces of emanation and the material cosmos. The ideal condition sought by the Jewish mystic is a loving union or communion with the Deity, a blending into a harmonious whole of the human and Divine wills, issuing in ecstasy and symbolized by the 'Kiss of Love'. This 'Kiss', which unites the soul to God, is usually ascribed to the seventh palace and is said to be of such intensity that it may draw the soul out of the body to God, even causing physical death. In European Alchemy, after nigredo follow the stages of albedo (Purgative Way, Moon), citrinitas (Illuminative Way, Sun) and finally rubedo (Unitive Way). The ultimate goal of the alchemists was transmutation into spiritual 'Gold' or the 'lapis philosophorum', which was achieved through seven operations or stages (Calcination, Dissolution, Separation, Conjunction, Fermentation, Distillation and Coagulation). These seven sequential steps created a pathway to union with the Divine self or higher consciousness. Finding the 'lapis philosophorum' meant finding one's true Self, the divine spark or 'scintilla animae' within (see also The Truth Within: A History of Inwardness in Christianity, Hinduism, and Buddhism, Gavin Flood, Oxford University Press, 2013, p. 95 and Oriental Thought: An Introduction to the Philosophical and Religious Thought of Asia, Yong Choon Kim, David H. Freeman, Rowman & Littlefield, 1981, p. 16 and Islamic Mysticism: A Short History, Alexander Knysh, BRILL, 2010, Chapter Ten and Introduction to Sufism: The Inner Path of Islam, Eric Geoffroy, Roger Gaetani, World Wisdom, Inc, 2010, p. 14 and Kabbalah: An Introduction to Jewish Mysticism, Byron L. Sherwin, Rowman & Littlefield, 2006, p. 86 and Commentarium in Ezechielem, Hieronymus, I 7 in Patrologia Latina, vol. 25, col. 22 b and The Great German Mystics: Eckhart, Tauler and Suso, James M. Clark, Courier Corporation, 2013, p. 19 and The Collected Works of C. G. Jung: Mysterium coniunctionis, an inquiry into the separation and synthesis of psychic opposites in alchemy, Carl Gustav Jung, Herbert Read, Michael Scott Montague Fordham, Gerhard Adler, Pantheon Books, 1970, p. 493 and The Role of Revelation in the World's Religions, Beverly Moon, McFarland, 2010, p. 156 and Spring, Analytical Psychology Club of New York., 1975, p. 191).
The threefold path of mystical ascent has a parallel in the Hindu Triple Path to Liberation of Karma Marga ("path of ritual action" or "path of duties"), Jnana Marga ("path of knowledge") and Bhakti Marga ("path of devotion") of oriental mysticism. Hindu's can chose to follow one or more of these paths according to their talents. The paths form the mukti marga or the Way of Liberation which is the triple path of purification, illumination, and union. In Hinduism, the ultimate goal for human beings is Moksha or Mukti, meaning liberation. In Hinduism liberation means liberation of the individual soul from Saṃsāra or the cycle of births and deaths, from the sense of duality and separation, and union with Brahman, the Supreme Soul or 'unio mystica'. Liberation means when a soul is released from its involvement with Prakriti or nature, which uses its instruments of delusion, attachment and egoism to subject the souls to their physical existence and the cycle of births and deaths. When the individual souls become aware of their true nature and transcend their limitations, they gain freedom and become one with the divine. In the Chandogya Upanishad (6.8.7) we find the concept of "तत्त्वमसि" (Tat Tvam Asi) as one of four Mahāvākyas (Grand Pronouncements), which according to Advaita means absolute equality of 'tat', the Ultimate Reality, Brahman, and 'tvam', the Self, Atman. The Self in its original, pure, primordial state is wholly or partially identifiable or identical with the Ultimate Reality that is the ground and origin of all phenomena (see also the Bhagavad Gita, ca. 100 CE and Early Buddhism and the Bhagavadgita, Kashi Nath Upadhyaya, Motilal Banarsidass Publ., 1997, p. 466 and Gandhian Alternative (vol. 3 : Socio-Political Thoughts), Anil Dutt Misra And Sushma Yadav, Concept Publishing Company, 2005, p. 117 and A Concise Encyclopedia of Hinduism, Klaus K. Klostermaier, Oneworld Publications, 2014 and Myths and Symbols in Indian Art and Civilization, Heinrich Robert Zimmer, Princeton University Press, 2015, p. 27 and New Perspectives on Advaita Vedānta: Essays in Commemoration of Professor Richard De Smet, S.J., Richard V. De Smet, Bradley J. Malkovsky, BRILL, 2000, p. 55).
The ascent through the three degrees of Freemasonry also has a similar structure as the spiritual ascent in Jewish Kabbalah, where the ascent is an opportunity given from Above to man to create in himself the desire necessary for spiritual growth, demonstrating through spiritual ascents and declines that the spiritual Light is pleasure and its absence is suffering. This path is known as "the path of the Kabbalah", or the path of the Light. The most characteristic and recognizable symbol of the Kabbalah is that of the ten sephirot. The sephirot contain many elements derived directly from Neoplatonic theologies and cosmologies, such as the metaphor of radiating light emanating from a blinding Godhead. There is also The 32 paths of wisdom, which is often included in the Sepher Yetzirah (Book of Formation). The 32 Paths of Wisdom refer to the 32 times that the name "Elohim" is mentioned in Genesis (Beresheet), Chapter One. The Sepher Yetzirah incorporates and seeks to explain these 32 Paths of Genesis. The Sepher Yetzirah reduces all of creation down to the 10 base numbers (sephirot) and 22 letters. it begins by stating that God created the universe through lamed-bet netivot, "thirty-two paths" of creation. The Sepher Yetzirah breaks down the Hebrew alphabet into three groups: the “mothers”, the “doubles”, and the “elementals”. The 32 paths are embedded into the Etz Chaim, the “Tree of Life”. The 10 circles on the “Tree of Life” correspond to the 10 sephirot, wich are interconnected by 22 lines, corresponding to the 22 letters. We can see that there is some resemblance to the degrees and symbolism of freemasonry, without going into detail (see also Sefer Yetzirah and The Path of Kabbalah, Michael Laitman, Ph.D., Rav Michael Laitman, Laitman Kabbalah Publishers, 2005, p. 47 and Basic Concepts in Kabbalah, Michael Laitman, Laitman Kabbalah Publishers, 2006, p. 17 and Neoplatonism and Jewish Thought, Lenn E. Goodman, SUNY Press, 2012, p. 331 and Judaism and Enlightenment, Adam Sutcliffe, Cambridge University Press, 2005, p. 148 and The 32 Paths of Wisdom, Rawn Clark, Journal of the Western Mystery Tradition, No. 3, Vol 1. Autumnal Equinox 2002 and Sefer Yetzirah and the 32 Paths of Creation).
The initiation and ascent from 'Entered Apprentice' to 'Master Mason' can also be compared to the scala amoris of the priestess Diotima of Mantinea in Plato's Symposium. The scala amoris describes the journey from the stage in life at which man can appreciate only particular or singular, deficient instances of beauty up to the point where man can view a plethora of beautiful objects, and finally divine Beauty itself. The ladder of love teaches man that the spiritual ranks higher than the physical, and the universal ranks above the particular. The ascent develops into a deepening and widening experience of beauty. He uses the metaphor of a staircase (ἐπαναβαθμοῖς) or ladder of ascent (Symp. 211c). Diotima explains the journey in Symp. 211c and 211d : "Beginning from obvious beauties he must for the sake of that highest beauty be ever climbing aloft, as on the rungs of a ladder, from one to two, and from two to all beautiful bodies; from personal beauty he proceeds to beautiful observances, from observance to beautiful learning, and from learning at last to that particular study which is concerned with the beautiful itself and that alone; so that in the end he comes to know the very essence of beauty. In that state of life above all others, my dear Socrates,' said the Mantinean woman, 'a man finds it truly worth while to live, as he contemplates essential beauty.". According to Diotima the true meaning of Love (Eros) is an aspiration for self-immortalization and for everlasting ownership of the Good and Beautiful. At the top of the ladder one is capable to see the Beautiful itself, absolute, untainted, genuine, untouched by any nonsense of humanity. In general four phases are being distinguished in the spiritual ascent alon the 'scala amoris'. At the first stage man learns to love the beauty of one body as a necessary stage to begin the ascent. In the Ode an die Freude we find the words 'Wem der große Wurf gelungen, Eines Freundes Freund zu sein, Wer ein holdes Weib errungen, Mische seinen Jubel ein!', which can for the sake of simplicity be considered as the prerequisite for the entry point of the ascent. This stage is the stage before the initiation as 'Entered Apprentice'. The second stage brings man to love of the beauty of the soul as part of the introspection of the 'Entered Apprentice'. The third stage brings man to the love of the beauty of the sciences or artes liberales which is the stage of the 'Fellow-Craft' degree. The fourth stage is the vision of Beauty itself at the stage of the 'Master Mason'. This stage involves the ascent form observance to beautiful learning to the science of nothing other than beauty itself or 'αὐτοῦ ἐκείνου τοῦ καλοῦ μάθημα' (autou ekeinou tou kalou mathêma) 'or science of beauty' (Symp. 211d). The true final stage of the journey, the vision of 'The Good' happens suddenly, which in Greek is called ἐξαίφνης (exaiphnés), meaning a radical conversion of mind or 'sudden seeing'. This final stage is being prepared for by the previous stages, but it does not follow automatically. In Christian theology this stage would be the 'visio beatifica'. The Symposium also inspired Marsilio Ficino (1433-1499 CE) to the De Amore and the Neoplatonic concept of amor platonicus as a kind of love which Ficino defines as a personal ability to guides one's soul towards cosmic processes and lofty spiritual goals and heavenly ideas (see also Plato on Love, Plato, C. D. C. Reeve, Hackett Publishing, 2006, p. xxxii and Eros en de filosofie: Plato's symposium : analyse en interpretatie, Rudi A. te Velde, Damon, 2006, p. 124 and Die Renaissance als erste Aufklärung, Volume 2, Mohr Siebeck, 1998, p. 50 and Studies on Plato, Aristotle and Proclus: The Collected Essays on Ancient Philosophy of John Cleary, John J. Cleary, BRILL, 2013, p. 65).
http://www.vanosta.be/pcrfrat_4b.htm |
|
|
 Primer Primer
 Anterior
34 a 48 de 48
Siguiente Anterior
34 a 48 de 48
Siguiente
 Último
Último

|
|
| |
|
|
©2026 - Gabitos - Todos los derechos reservados | |
|
|

