BORROMEAN RINGS (1/3)
BORROMEAN RINGS
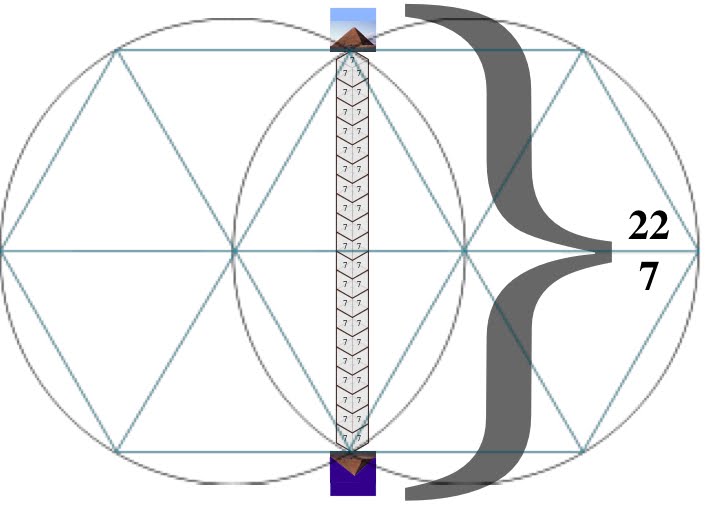
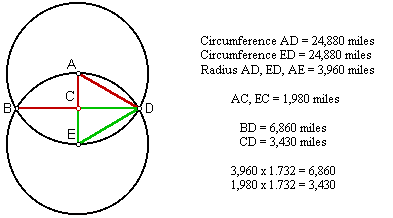
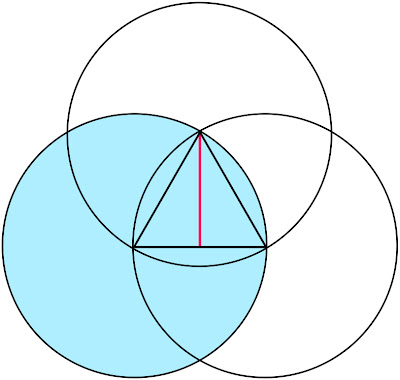
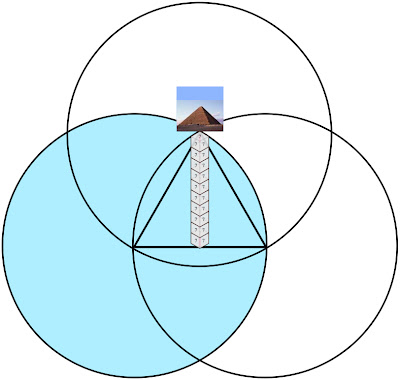
3 Rings linked together, their centers being vertices (corners) of an equilateral Triangle.
Viewed in this diagram, we are looking at a 2-dimensional map of Earth from its side, represented by One ring of our choosing (blue):
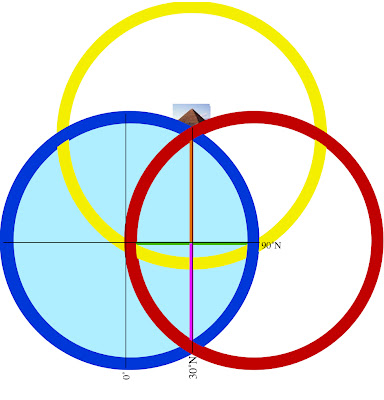
Orient the planet so the Great Pyramid at Giza (30˚N) lays at one of the vertices, the Earth’s center at another, and its axis’ North pole at the third.
Exploring this set of relations, it can be demonstrated that the architectural proportions of the Great Pyramid at Giza exhibit a means of utilizing the measure of Earth to express the mathematical constant, π. To understand how we must suspend, for a moment, our habit of thinking of number in purely quantitative terms and consider the ways in which some numbers are also inherently bound to specific geometric forms - like with ‘square’ (1² 2² 3² 4² 5²...) or ‘cubed’ (1³ 2³ 3³ 4³ 5³...) numbers we see a sum attached to a particular shape. Other shapes each possess their own sequence of numbers also attached to their change in proportion.
These are called ‘figurate numbers’, and tradition has it they were introduced into Greek mathematics by the pre-Socratic philosopher, Pythagoras, in the 6th century BC. A student of the ancient mystery schools, it is likely he acquired this knowledge during his journeys to Chaldea & Egypt; but all that is really required to calculate the number sequences tied to these shapes is a stack of pebbles and time to spare, counting out the variety of polygons & devising ways of stacking them to construct polyhedrons.
To the careful interpreter of nature a pattern was discernible amidst this numerical data - One that, properly placed, could be applied to the measure of all things. It is suggested here that the Great Pyramid at Giza, in relation to the 3-Ring structure given above, embodies this application.
Let us then imagine the Great Pyramid as keystone to a system of ‘projective numerology’ - an application of mathematics using figurate numbers to model distances and proportions as shapes, and translating them into their related forms as ‘seen’ from different angles & in other dimensions.
At the root of any square pyramid’s architecture is its’ seked - an ancient Egyptian ratio of angular measure used to determine the slope of a pyramid’s sides and thus its’ height.

Utilizing the seked of the Great Pyramid, the perimeter of a square pyramidal base equals the circumference of a circle whose radius is equal to that pyramid’s height.
Within our 2-dimensional map, as our planet rotates upon its’ axis, the Pyramid appears to move from one end of a vesica piscis to the other, as if turning on a Wheel whose rim is the 30th parallel. Thus, in one quarter turn (11/14 ≈ π/4) the Pyramid appears to move in a perpendicular line to the base of the equilateral Triangle articulated within our 3-ring diagram.

The distance of this perpendicular line from the Great Pyramid to the Earth’s polar axis is 3430 nautical miles, or 10x the cube of seven.
Let us then imagine this distance as a stack of 10 cubes, 7x7x7.

A ‘quarter turn’ (11/14) of the Earth thus ‘apportions’ a 10x10 square of these cubes:
10² x 14/11 = 127.27272727...
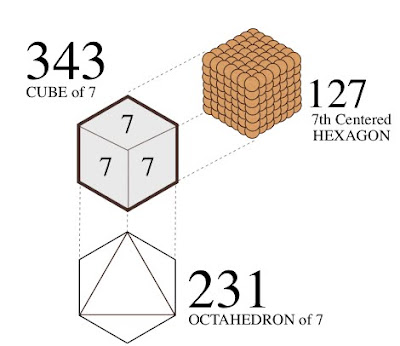 [3d:2d = 343 : 127 ]
[3d:2d = 343 : 127 ]As such, we can picture the square pyramid monument atop this ‘column’ as pointing to the center of an imaginary 11th cube.
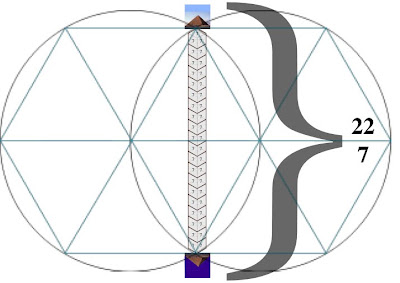
It follows, then, that a 12-hour rotation (180˚) measures a distance from center-point to center-point of the cubes at either end of a column 22 cubes of 7 long.
The center point of a unit cube has a specific relationship to the vesica piscis traversed in this 12-hour ‘distance’ within our diagram, as Two rings sharing a single radius give a rational approximation for √3, which is also the space diagonal of any unit cube.
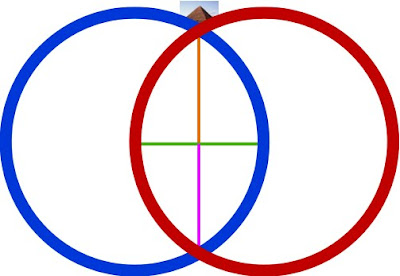
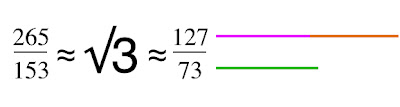
In other words, with respect to a unit cube, the √3 is the distance between opposite corners of that cube. Tracing these space diagonal lines joins the opposing corners, all of which intersect at the center of that cube, and thereby delineate the edges of six square pyramids joined at their apex.
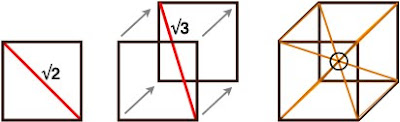
22:7 ≈ π
To the Egyptian god Thoth, equated with the Greek god, Hermes, and particularly the Roman god, Mercury, this ratio is significant in describing the number of conjunctions aligning Mercury & Earth with the Sun every 7 years. Also known as a ‘synodic cycle’, this is an example of what ancient Greek astronomers called an exeligmos, or ‘Turn of the Wheel’ - describing any period wherein Sun, Moon, and/or planets return to conjunction(s) from which they started. The term is still used today, but is more specifically applied to the Triple Saros cycle of reckoning lunar eclipses, each 120º of longitude apart, eventually returning to a point relatively close to where they began: exeligmos. The Romans used the term annus magnus, or ‘great year’ to describe the same class of periodic event.
As we shall see, each of the planets have a harmonic ratio of conjunctions with our planet Earth, and with each other. By fixing the Earth to the center of our ecliptic plane, the motion of other planets relative to our position appear as serpentine spiro-graph patterns, looping in close when aligning into conjunction with the Sun, and looping out to trace a wide arc that coils about the Earth until looping in again for another conjunction.
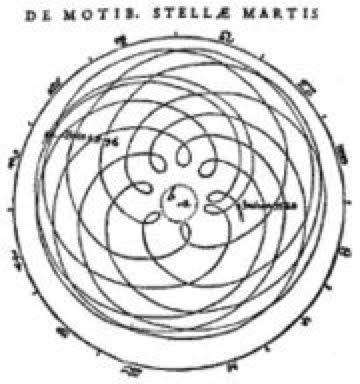
Mars:Earth

Venus: Earth
Consistent within our model of 10 cubes of seven, the Great Pyramid (pointing to the center of an eleventh) also corresponds to the tip of an octahedron of 7 = 231. And it just so happens that 11x 231 is the number of days in the exeligmos of Mercury & Earth, 22:7. In addition, the measure of the Great Pyramid’s base side lengths (440 cubits each) give a total base area measuring approximately 231 meters square.
Being a close approximation of the value π, and our annus magnus with the planet Mercury (Hermes/Thoth), let us then imagine this column of 22 cubes of 7 as the staff of his Caduceus. As we shall see, the cycles of the other planets can be represented as the serpents entwined about this Staff, their helices in tune with the ratio of their exeligmos.
Imparting more than just the inevitable passage of Time, they were the very music of the spheres by which the harmony of creation was made known to the ancient Geometers. Our 3-Rings establish the base unit of an entire system of weights & measures (metrology) by symbolizing an angular dimension constructed by the movement through Time of the Great Pyramid, like the point of a metronome entrained to the Earth’s tempo. In effect attuning the mathematical constant π with Mercury's Great Year & the linear measure of Earth's size in units of angular measure. 'Squaring' the circle much like the Great Pyramid's seked.
1 nautical mile = 1.15 miles
The nautical mile used as our base unit of measure for obtaining the distance in cubes of seven is also a unit of angular measure equivalent to 1/60th degree of Earth longitude (=1 minute of arc degree). Converting this into survey land miles = 1/10² the number of days between Earth:Mercury conjunctions (=115).
22:7 = 12 hrs @ 30˚north (12x 30 = 360)
180˚ = 10,800 arc minutes of degree = 50x 216, the cube of 6
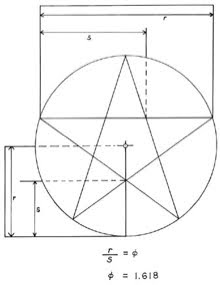
216 also equals the number of degrees between Earth:Venus conjunctions (x5 = 1 Earth:Venus pentagram = exeligmos). So, by subdividing each degree of arc into 60 minutes, Earth’s 180˚ rotation (22:7) upon its’ axis thereby possesses a kind of numerological resonance regarding its harmonic with Venus, the exeligmos of the pentagram. Reputedly a symbol of good will among the Pythagoreans, the pentagram also provides an easy means of obtaining the golden ratio.
12 : 1 = (22/7) = 60 minutes
In this way our measure of both Time & Space define each other by weaving together the value π with the ‘divine proportion’ of the golden ratio.
Of the numerous other curious facets to this TooL of Hermetic Metrology, establishing not only our system of weights & measures, its choice of cubes & octahedrons also exhibit a direct connection to speeds of both sound & light:
1 meter
=distance trave1ed by sound 1/343th of second
=distance trave1ed by light 1/299,792,458th of second
343 = cube of 7
299,792,458 = c = speed of light in meters per second
1296000 / π = number of square degrees in one whole sphere
c / 1296000 = 231.321....
231 = octahedron of 7
Stranger still, the proportions outlined above are also paralleled in the numerical structure of the Tarot de Marseilles’ pattern of 22 major arcana trumps when applied to the Hebrew alphabet - in turn derived from Egyptian (via proto-Sinaitic) hieroglyphs which depicted the symbols those letters are still associated with.
We see traces of this tradition within our own English alphabet with the letter A: also the glyph for an Ox head (turned upside-down) having the same origin as the Hebrew letter aleph.

Referred to by 'occultists' as the Book of Thoth (though never adequately explained why), the key to unlocking this puzzle, as with any cryptological TooL, is knowing where to place the cypher, or sifr - the arabic word from which we also get Zero, or ‘nothing’, the rank of every Tarot deck’s Fool [aleph=0].
And this role proves more than suitable for One who ushers in what ultimately reveals a prank, of sorts... leading to what is arguably the greatest punch-line in history.