|
|
General: 1 DE REYES 7:22=3.14="EXPERIMENTO FILADELFIA"="MAQUINA DEL TIEMPO"
Elegir otro panel de mensajes |
|
|
Contexto
La obra de Hiram en el templo…21Erigió, pues, las columnas en el pórtico de la nave; erigió la columna derecha y la llamó Jaquín, y erigió la columna izquierda y la llamó Boaz. 22Y en lo alto de las columnas había lirios tallados. Así fue terminada la obra de las columnas.
Referencia Cruzada
1 Reyes 7:19Los capiteles que estaban en las cabezas de las columnas del pórtico tenían forma de lirios, y medían cuatro codos.
1 Reyes 7:21Erigió, pues, las columnas en el pórtico de la nave; erigió la columna derecha y la llamó Jaquín, y erigió la columna izquierda y la llamó Boaz.

| Reply |
Message 13 of 18 on the subject |
|
|
|
|
| Reply |
Message 14 of 18 on the subject |
|
|
|
|
| Reply |
Message 15 of 18 on the subject |
|
|
|
|
| Reply |
Message 16 of 18 on the subject |
|
|
|
|
|
|
|
| Reply |
Message 109 of 109 on the subject |
|
| Reply |
Message 6 of 18 on the subject |
|
|
|
|
| Reply |
Message 7 of 18 on the subject |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Reply |
Message 31 of 31 on the subject |
|
|
| Reply |
Message 71 of 73 on the subject |
|
|
|
|
| Reply |
Message 72 of 73 on the subject |
|
|
|
|
| Reply |
Message 73 of 73 on the subject |
|
|
Geometry
Geometry of the Great Pyramid
DIMENSIONS of Great Pyramid
by morphvs
The following article is Copyright © 2001-2003 aiwaz.net_institute.
All rights reserved. No part of this website, including text and images, may be reproduced or copied
in any form or by any means without the express prior written permission of aiwaz.net_institute.
Presented with permission.
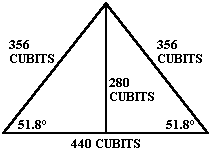
If the calculations concerning the royal cubit are correct the main dimensions of the pyramid should also prove that. The approximate dimensions of the pyramid are calculated by Petrie according to the remains of the sockets in the ground for the casing stones whose remains are still at the top of the pyramid, and the angle 51° 52' ± 2' of the slopes. The base of 9069 inches is approximately 440 royal cubits (the difference is 9 inches which is not a remarkable difference if we consider the whole dimension and consider that the employed data represent only an estimation of the real values) whereas the calculated height, 5776 inches, is precisely 280 royal cubits. The relation 440:280 can be reduced to 11:7, which gives an approximation of the half value of Pi.
Squaring the Circle

The circle and the square are
united through the circumference:
440x4=1760=2x22/7x280
area of square: 440x440=193600
area of circle:28x28x22/7=246400
sum: 440000
|
The engagement of Pi value in the main dimensions suggests also a very accurate angle of 51° 52' ± 2' of the slopes which expresses the value of Pi. Another coincidence is the relation between the height of the pyramid's triangle in relation to a half of the side of the pyramid, since it appears to be the Golden Section, or the specific ratio ruling this set of proportions, F = (sqr(5)+1)/2 = 1.618 = 356:220. This ratio, 356:220 = 89:55 is also contained in the first of Fibonacci Series:
1 2 3 5 8 13 21 34 55 89 144 ...
A single composition contains two apparently contradicting irrational numbers P and F, without disrupting each other. This appears to be completely opposed to the classical architectural canon which postulates that in 'good' composition no two different geometrical systems of proportions may be mixed in order to maintain the purity of design.
But analysis of other architectural and artistic forms suggested that the greatest masters skillfully juggled the proportional canons without losing the coherent system, for they knew that these systems can be interconnected if the path that links them is found. That is obvious In the case of the Great Pyramid where two different principles are interweaved without interference ruling different angles of the composition, which is most importantly a most simple one, namely 11:7, a most simple ratio obviously signifying such infinite mysteries as the value of P and most 'natural' value of F. In spite of common miss-understanding of architectural composition, the most mysterious and praised compositions are very simple but not devoid of anthropomorphic appeal, since everything is made out of human proportions, just like Vitruvius describing the rations of the human body, very simple and very clean. The numbers 7 and in 11 are successive factors in the second of Fibonacci progressions that approximate geometry of the pentagram:
1 3 4 7 11 18 29 47 76 123 ...
The summary of the selected main mean dimensions is:
|
dimension
|
b. inch
|
m
|
royal cub.
|
palm
|
digit
|
|
base
|
9068.8
|
230.35
|
440
|
3,080
|
12,320
|
|
height
|
5776
|
146.71
|
280
|
1,960
|
7,840
|
|
sum
|
|
|
720
|
|
20,160
|
|
slope
|
7343.2
|
186.52
|
356
|
2,492
|
9,968
|
|
edge
|
8630.4
|
219.21
|
418
|
2,926
|
11,704
|

The main source of all kinds of delusions and speculations about our mythical past for the western man comes of course from Plato. With the myth of Atlantis he planted the necessary seed of mythical Eden, a culture of high intelligence that lived before the known history. If Plato received any wisdom from the ancient Egypt it could perhaps be traced in the canon of numbers that is so latently present throughout his work, but never on the surface. This canon seems to appear in the descriptions of his fantastic cities where everything is most carefully calculated and proportioned. The topic of Plato's Laws is the description of the ideal state called Magnesia which is entirely composed out of the mysterious number 5,040.
The distance* when Earth is closest to Sun (perihelion) is 147x106 km, which is translated into royal cubits 280x109, hinting at the height of the Great pyramid,
280 royal cubits.
The above article comes from aiwaz.net_institute - Great Pyramid and Giza plateau
and is Copyright © 2001-2003 aiwaz.net_institute. All rights reserved.
No part of this article, including text and images, may be reproduced or copied in any form
or by any means without the express prior written permission of aiwaz.net_institute. Reprinted with permission.
* Related links: Astronomic & Cosmographic Data, Nasa site with planetary data
Do not miss this web site: aiwaz.net_institute - Great Pyramid and Giza plateau
Find out more amazing facts about the GREAT PYRAMID: Position of King's Chamber, Queen's Chamber, Subterranean Chamber; SECOND PYRAMID: Dimensions of Pyramid, Great Chamber, Coffer, Lower Chamber; THIRD PYRAMID: Dimensions of Pyramid, Chambers,MATHESIS of Giza Plateau.
The Golden Ratio & Squaring the Circle in the Great Pyramid
A straight line is said to have been cut in extreme and mean ratio when,
as the whole line is to the greater segment, so is the greater to the less. [Euclid]
The extreme and mean ratio is also known as the golden ratio.

If the smaller part = 1, and larger part = G, the golden ratio requires that
G is equal approximately 1.6180
Does the Great Pyramid contain the Golden Ratio?
Assuming that the height of the GP = 146.515 m, and base = 230.363 m, and using simple math
we find that half of the base is 115.182 m and the "slant height" is 186.369 m
Dividing the "slant height" (186.369m) by "half base" (115.182m) gives = 1.6180, which is practically equal to the golden ration!
The earth/moon relationship is the only one in our solar system that contains this unique golden section ratio that "squares the circle". Along with this is the phenomenon that the moon and the sun appear to be the same size, most clearly noticed during an eclipse. This too is true only from earth's vantage point…No other planet/moon relationship in our solar system can make this claim.
Although the problem of squaring the circle was proven mathematically impossible in the 19th century (as pi, being irrational, cannot be exactly measured), the Earth, the moon, and the Great Pyramid, are all coming about as close as you can get to the solution!
If the base of the Great Pyramid is equated with the diameter of the earth, then the radius of the moon can be generated by subtracting the radius of the earth from the height of the pyramid (see the picture below).

Click here to view larger picture.
Also the square (in orange), with the side equal to the radius of the Earth, and the circle (in blue),
with radius equal to the radius of the Earth plus the radius of the moon, are very nearly equal in perimeters:
Orange Square Perimeter = 2+2+2+2=8
Blue Circle Circumference = 2*pi*1.273=8
Note:
Earth, Radius, Mean = 6,370,973.27862 m *
Moon, Radius, Mean = 1,738,000 m.*
Moon Radius divided by Earth Radius = 0.2728 *
* Source: Astronomic and Cosmographic Data
Let's re-phrase the above arguments **

In the diagram above, the big triangle is the same proportion and angle of the Great Pyramid, with its base angles at 51 degrees 51 minutes. If you bisect this triangle and assign a value of 1 to each base, then the hypotenuse (the side opposite the right angle) equals phi (1.618..) and the perpendicular side equals the square root of phi. And that’s not all. A circle is drawn with it’s centre and diameter the same as the base of the large triangle. This represents the circumference of the earth. A square is then drawn to touch the outside of the earth circle. A second circle is then drawn around the first one, with its circumference equal to the perimeter of the square. (The squaring of the circle.) This new circle will actually pass exactly through the apex of the pyramid. And now the “wow”: A circle drawn with its centre at the apex of the pyramid and its radius just long enough to touch the earth circle, will have the circumference of the moon! Neat, huh! And the small triangle formed by the moon and the earth square will be a perfect 345 triangle (which doesn’t seem to mean much.)
** Source: http://geometry.wholesomebalance.com/Sacred_Geometry_2.html#Phi
Recommend this website to your friends:

Was the golden ratio intentionally built into the Great Pyramid of Cheops?
Why would anyone intentionally build the golden ratio into a pyramid, or other structure? What was the significance of to the Egyptians? And did the ancient Egyptians intentionally design the Great Pyramid to square the circle?
The answer to these questions is uncertain since designing the Great Pyramid according to the simple rules explained by the graphic below would give the pyramid automatically (by coincidence? ) all its "magic" qualities.
The height of the Great Pyramid times 2π exactly equals the perimeter of the pyramid. This proportions result from elegant design of the pyramid with the height equal two diameters of a circle and the base equal to the circumference of the circle. Click here or on the image below to see larger picture.



For the angle of the Great Pyramid, any theory of the base, combined with any theory of the height, yields a theoretic angle; but the angles actually proposed are the following** :
|
Angle of casing measured
By theory of 34 slope to 21 base
Height : circumference :: radius to circle
9 height on 10 base diagonally
7 height to 22 circumference
area of face = area of height squared
(or sine) = cotangent, and many other relations)
2 height vertical to 3 height diagonal
5 height on 4 base
|
51º 52' ± 2' (51.867)
51º 51' 20"
51º 51' 14.3"
51º 50' 39.1"
51º 50' 34.0"
51º 49' 38.3"
51º 40' 16.2"
51º 20' 25"
|
** Page 184, The Pyramids and Temples of Gizeh
by Sir W.M.Flinders Petrie 1883
Giza Alignment Code - The Time Temple
A silent message from 5000 years ago. From a letter to a scientist:
"The conclusion should be made upon a probability, that it may be just coincidental, that these 14 lines are forming a very accurate model of the inner planetary system, showing also a precise time position, that coincidentally matches (relative to the end of Mayan Calendar) the beginning of the final 1260 days time period, mentioned both in the Old and New Testament (surely one of the most remarkable and disputed episodes in the Book), a time period, which allows (and was supposedly measured for) to show in a relatively short period of time, when, and what the End is all about - the mystery of death and the origin of life.
http://old.world-mysteries.com/mpl_2.htm
|
|
|
|
|
|
|
|
|
 Primer Primer
 Anterior
59 a 73 de 568
Siguiente Anterior
59 a 73 de 568
Siguiente Último
Último
|
|
| |
|
|
©2024 - Gabitos - Todos los derechos reservados | |
|
|