|
|
General: NUMERO DE LA PLATA (RELACION CON EL OCTOGONO)=√2 = 1,414213562
Elegir otro panel de mensajes |
|
|

Haz clic en la imagen para volver
INICIACIÓN A LOS NÚMEROS DE LA ARQUITECTURA O DE COMO DARLE FORMA A UN EDIFICIO
Los números pueden estar explicados matemáticamente en la “red” pero el problema que plantea el conocimiento de la arquitectura es: ¿cómo se le da forma con esos números a un edificio?. En arquitectura los números operan a partir de los polígonos estrellados formando concatenaciones, tal y como a continuación vamos a describir.

NÚMERO DE ORO - PENTÁGONO
El número de oro viene dado por la solución a la ecuación de segundo grado
x + x² = 1 x = 1+√5 /2 = 1,618033989
Propiedades 1/ 1,618 = 0,618 1,618... x 1,618... = 2,618...
Dado una circunferencia de radio 1 el lado del decágono inscrito en él es 0,618...
Dado un pentágono de lado 1, las diagonales de ese pentágono = 1,618...
La técnica con la que opera la arquitectura es la de las concatenaciones.
Una de ellas, la más usual, es la que presentamos en el dibujo. Si la circunferencia en color azul tiene R=1 el radio de la roja es R= 2,618, correspondiente a la que presentamos en “El vitruvio” de Leonardo da Vinci en la portada de este trabajo.
Se aplicará en la restitución de una tabla de F. Brunelleschi Nº 6.
 
NÚMERO DE PLATA - EL OCTÓGONO
Así como el número de oro está asociado a la √5 el número de plata está asociado a √2 y presenta una serie de propiedades similares a las del número de oro.
√2 = 1,414213562 tg. 22,5º = 0,414213562
tg.67,5º = 2,414213562
1/2,4142... = 0,4142... 2,4142... x 1,4142... = 3,4142...
Observa nuevamente la concatenación, esta vez con el octógono, de la circunferencia en color azul sobre la de color rojo.
Si el radio de la circunferencia azul es 1 la de color rojo es 2,4142....
Si el radio de la circunferencia azul es 0,4142... la de rojo es 1.
Aquí tenéis un ejemplo.
Se aplicará en la Rix House de J. Soane Nº 3.
NÚMERO DE PLATINO - EL HEXÁGONO
De igual forma que el número de oro está relacionado con la √5 y el de plata con la √2, el de platino lo va a estar con la √3
√3 = tg.60º = 1,732050808
1,732... x 2,732... = 4,732...
Combinación, esta, muy utilizada por Andrea Palladio.
Observa la concatenación de la circunferencia azul sobre la de rojo, a través del hexágono, directamente a la circunferencia azul. Si el radio de la circunferencia color azul es 1 el de la circunferencia en color rojo es 2 y el lado del triángulo inscrito es 2 x 1,732...
Este polígono es el más prolífico en la historia de arquitectura como vamos a verlo en los ejercicios.
Aquí tenéis un ejemplo.
Se aplicará al resto de los trabajos Nº 1 - 2 - 4 y 5.
Todos los derechos reservados. Depósito Legal ZA - Nº 69 - 1998
Página web optimizada para ver en resolución de 1024 x 768
2006 - 2007
|
|
|
|
|
+ la rueda de la vida Los Bosques - Viviendo lo invisible para recordar quiénes somos | Living the unseen to remember who we are--atención es una clave milenaria impresa en nuestro sub/incosciente..su sólo aprecio visual es pura influencia en el núcleo del átomo de los componentes silíceos de nuestro tejido neuronal sometido a la gravidez terráquea 
 |
Click para ampliar |
 - nuestra cruz del sur ..celeste.  Read English version here En el Sur, cuando alcanzamos el Aquietamiento (primeros días de mayo) en la Rueda de la Vida Solar , iniciamos la última fase de nuestro año (en el Norte inician el Crecimiento). Mientras nos acercamos a los días más oscuros del año, los pliegues entre mundos se tornan más sutiles, activando vórtices y permitiendo mayor comunicación con los mundos que no se ven. Es momento de retornar a los orígenes, honrar a los ancestros y solicitar su guía; aunque debido a Desvinculaciones con la Rueda de la Vida celebramos esto junto al Hemisferio Norte en el Día de los Muertos en noviembre, que es cuando allá se da su Aquietamiento. En esta Cuarta Media Estación u Octava Fase de la Rueda de la Vida en el Sur, es que se celebra en numerosos pueblos y territorios la Fiesta de la Cruz, haciendo referencia y siguiendo el curso de la constelación Cruz del Sur que es nuestra Rueda de la Vida manifiesta en los cielos.los 60 grados representados..:  La Cruz del Sur es nuestra Rueda de la Vida manifiesta en los cielos con sus 4 estrellas principales (alfa Cruz, beta Cruz, delta Cruz y gama Cruz) formando sus posiciones una cruz y casi orientándose a los 4 puntos cardinales cuando su eje mayor se yergue verticalmente sobre nosotros, justamente en los primeros días de mayo. Y, los otros 4 puntos de la rueda lo conforman los puntos intermedios como lo reflejó Huaman Poma. (Milla, 1995) la proporcion sagrada 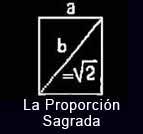 A partir de la Cruz del Sur los pueblos andinos distribuyeron sus territorios: A partir de la Cruz del Sur los pueblos andinos distribuyeron sus territorios:
“…en la época precerámica, del estado comunitario andino conocido como Pusisuyu, en aymara o Tawantinsuyu en idioma quechua o runasimi. “El pusisuyu fue el Wiñaymarca, o sea las mancomunidades de los cuatro puntos cardinales, eran contínuas, eternas en sentido referido al total contenido del sistema jakaña comunitario”. Las orientaciones y el número de sus 4 regiones o suyus están ligados a las 4 estrellas de la constelación de la Cruz del Sur. El ombligo, Ccosco o Taypicala sería el punto de cruce de ambos brazos y estaría situado en Tiwanaku originalmente.” (Milla, 1995- sigamos con el rombo premonitorio 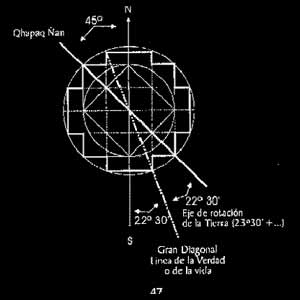 La solución geométrico matemática de la Chakana es fractal como se refleja en gorros rituales, legados arqueológicos, cerámica y la whipala. - Fractal igualmente puedenser los decaedros -sin- espacios intermedios- que inspiradamente construyen las abejas para "guardar" el néctar.. 
Última edición por MICROLITO; 03-abr-2012 a las 19:33
|
|
|
|
|
The Great Pyramid and the Speed of Light
The Great Pyramid encodes enormous amount of numerical coincidences ( pi, Phi, dimensions and movement of our planet, axial tilt, precession, speed of light, and more…)
We can only wonder if the ancient architects were fully aware of these special numbers encoded in their design — or are these numbers simply the result of selecting 2 numbers (7 and 11) for proportions for the Great Pyramid???
|
|
The design of the Great Pyramid is based on the ratio 11:7. This ratio (equal 1.571) is perfect approximation of the “squaring the circle” principle.

For the Great Pyramid, Base to Height Ratio 440/280 is exactly 11/7
Most “pyramidologists” appear to be “chasing their tails” uncovering huge amount of “numerical coincidences” embedded in the Great Pyramid…
It is simply unbelievable, however ALL of these numerical coincidences are result of selecting just 4 numbers for the pyramid design: 7, 11 (height to base ratio), 40 (the scale factor), and the 4th key number is the value of the measuring unit: Royal Cubit = 20.62 ” = 0.524 m.
|
This single, fundamental design principle: 11 : 7 Base to Height Ratio generates ALL amazing mathematical properties of the Great Pyramid:
- the Golden Ratio Phi=1.618 (the Great Pyramid is a Golden Pyramid: length of the slope side (356) divided by half of the side (440/2 = 220) height is equal to 1.6181818… which is the Golden Ratio Phi
- squaring the circle ratio 1.571 (base/height = 44/28 = 1.571)
- pi=3.14159… (2 x base/height = 2 x 44/28 = 3.14286 which is very close approximation of “pi” = 3.14159…)
- Perimeter of the square base, 4×440=1760, is the same as circumference of the circle with radius = height: 2x ”pi” x height (2x 22/7 x 280=1760)
- The ratio of the perimeter to height of 1760/280 cubits equates to 2x pi
to an accuracy of better than 0.05%
- Side of the base (440) plus double height (2x 280=560) = 1,000
- Perimeter of the square base is equal 4×440=1760 RC = 0.5 nautical mile = 1/7,200th of the radius length of the earth
- the slop angle 51°.843
- The Pyramid exhibits in the design both pi and by Phi, given the similarity
of 2/ sqrt(phi) (2 divided by the square root of Phi) with pi/2 :
- 11/ 7 equal 1.5714
- 2/ sqrt(89/55) equal 1.5722
- 2/ sqrt(Phi) equal 1.5723
- pi/ 2 equal 1.5708
- Royal Cubit = 0.5236 m, pi – Phi2 = 0.5231
- and more…
Does Great Pyramid encode “fractal” value of the speed of light?
The speed of light in a vacuum is 299, 792, 458 meters per second or 983,571,056.43045 feet per second or 186,282.397 miles per second.
Base of the Great Pyramid is a square with side B = 44o Royal Egyptian Cubits. Let’s draw two circles: one inscribed and one superscribed on the square of the base of the Great Pyramid.

- Circumference of superscribed circle: 2x pi x R
- Circumference of the inscribed circle: 2x pi x r
The difference of the circumference of both circles (lets call it C) is:
C = 2 x pi x (R – r) = 2 x pi x [ B/sqrt(2) - B/2 ] =
2x pi x B x [ 1/sqrt(2) - 1/2 ] = 1.301290285 x B
The length of the Egyptian Royal Cubit
Based on “The Pyramids and Temples of Gizeh” by W.M. Flinders Petrie. 1883.
The unit of measuring length used by the ancient architects in the construction of the Great Pyramid was the Royal Cubit.
Petrie estimated the value of the Royal Cubit using some key dimensions of the Great Pyramid:
By the base length of the Pyramid, if 440 cubits (section ’43): 20.611 ± .002
By the base of King’s Chamber, corrected for opening of joints: 20.632 ± .004 inches
By the Queen’s Chamber, if dimensions squared are in square cubits: 20.61 ± .020
By the antechamber: 20.58 ± .020
By the ascending and Queen’s Chamber passage lengths (section 149): 20.622 ± .002
By the gallery width: 20.605 ± .032
The Average value of the RC (based on above numbers) is 20.61 inches.
It’s almost universally accepted that archaeologist Flinders Petrie’s determination of the royal cubit length at 20.632 inches, from his measurements of the King’s Chamber in the Great Pyramid of Giza, was the likely measure to survey the dimensions of that pyramid, 440 royal cubits per base side, but the experts stop there, not then letting you know that those 1,760 royal cubits which total the Great Pyramid’s base perimeter length, when multiplied by 20.632 inches, equals half a modern nautical mile, or 1/7,200th of the radius length of the earth, so there certainly is a connection.
EL EXAGONO Y LA RELACION CON EL PI=22/7-LAS MATEMATICAS CONFIRMAN LA RELACION EXAGONAL CON MARIA LA MAGDALENA EN EL MISMO DIA DE SU DIA EN LA IGLESIA CATOLICA, OSEA EL 22 DE JULIO (22/7)
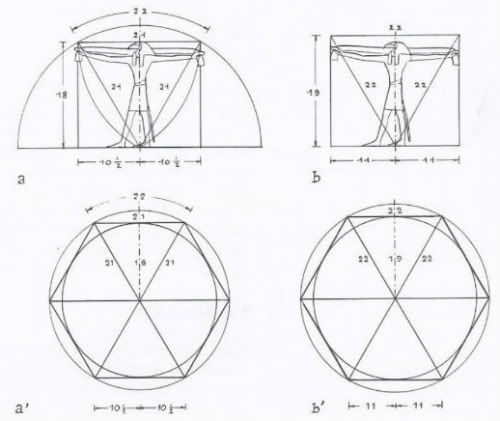 Temple of Man Schwaller de Lubicz page 177 Serpents in the Sky by John Anthony West Temple of Man Schwaller de Lubicz page 177 Serpents in the Sky by John Anthony West
Noten que tenemos el SECTOR CIRCULAR, en un contexto matematico exagonal, la relacion matematica 22/11. Sabemos que la longitud de la circunferencia es igual al numero PI=3.14=22/7 por el DIAMETRO=RADIO*2 del circulo. En un contexto a que tenemos segun la figura superior la LONGITUD DE ARCO (PI/3-RADIANES) que es igual a 22 si hacemos las matematicas:
LONG. CIRC.=3.14*DIAMETRO=3.14*2*RADIO=22/7*2*21=22/7*2*7*3=(22*2*7*3)/7=22*6
LONG. CIRC.=22*6=132=33*4 (IMPRESIONANTE RELACION DEL NUMERO 33)
Noten que estamos haciendo referencia al exagono y es obvia su interrelacion con el planeta Mercurio, que insisto, esta interrelacionada con la ESTRELLA DE DAVID, OSEA EL HIJO DEL MISMO DAVID, QUE FUE EL REY SOL-O-MON. El 33, insisto, es una referencia a los dos triangulos, de la estrella de 6 puntas. Ahora, si la longitud del arco es igual a PI/3 (RADIANES) tenemos la relacion:
22/21=22/(7*3)=(22/7)/3=PI/3
IMPRESIONANTE DE QUE BELLAS SON LAS MATEMATICAS.
LA MISMA PALABRA REVOLU-SION ES UNA REFERENCIA AL NUMERO PI (LONGITUD DE LA CIRCUNFERENCIA ES IGUAL A PI X DIAMETRO.)
|
|
|
|
|
| COLOSO (Original message) |
Sent: 23/05/2017 12:50 |
6 x 6 ================================= 36 --- 3 + 6 = 9
6 + 6 + 6 =============================== 18 --- 1 + 8 = 9
666 x 3 ===== 1998 -------- 1+9+9+8 ========= 27 --- 2 + 7 = 9
666 x 192 === 127872 ----- 1+2+7+8+7+2 ===== 27 --- 2 + 7 = 9
666 x 1234 == 821844 ----- 8+2+1+8+4+4 ===== 27 --- 2 + 7 = 9
666 x 37583 = 25030278 --- 2+5+0+3+0+2+7+8 = 27 --- 2 + 7 = 9
666 x 8888 == 5919408 ---- 5+9+1+9+4+0+8 === 36 --- 3 + 6 = 9
APOCALIPSIS 13:18 Aquí Hay Sabiduría. Él Que Tiene Entendimiento, Cuente El Número De La Bestia, Pues Es Número De hombre. Y Su Número Es Seiscientos Sesenta y Seis. (666)
266 Días = 9 Meses Lunares = 36 Sábados Lunares = Gestación De Un Bebe.
9 Meses x 4 Sábados de Cada Mes = 36 Sábados Lunares.
1+2+3+4+5+6+7+8+9+10+11+12+13+..... 33+34+35+36 = 666
LEVÍTICO 18:21 Y No Des hijo Tuyo Para Ofrecerlo Por Fuego a Moloc; No Contamines Así El Nombre De Tu Dios. Yo Jehová.
LEVÍTICO 20:3 Y yo Pondré Mi Rostro Contra Él Tal Varón, y Lo Cortaré De Entre Su Pueblo, Por Cuanto Dio De Sus hijos a Moloc, Contaminando Mi Santuario y Profanando Mi Santo Nombre.
1 REYES 11:33 Por Cuanto Me Han Dejado, y Han Adorado a Astoret diosa De Los Sidonios, a Quemos dios De Moab, y a Moloc dios De Los hijos De Amón; y No Han Andado En Mis Caminos Para Hacer Lo Recto Delante De Mis Ojos, y Mis Estatutos y Mis Decretos, Como Hizo David Su Padre.
Sigue........
|
| From: Cajeli |
Sent: 11/11/2013 18:06 |
|
Esta es otra región de Marte, Cydonia Mensae a 33ºN y 13ºW

GGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGG
|
| Reply |
Message 5 of 5 on the subject |
|
|
|
| Reply |
Message 282 of 282 on the subject |
|
|
|
|
|
|
|
|
Washington DC: el Monumento a Washington = 8 y estrella octágono - la diosa sumeriana Inanna
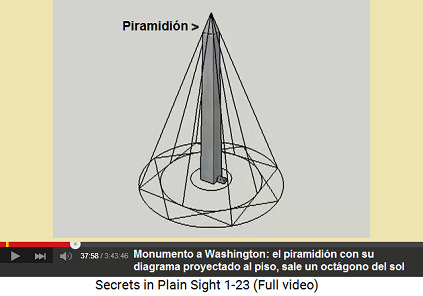 Monumento a Washington: el piramidión con su diagrama proyectado al piso, sale un octágono del sol
Bernard I. Pietsch detectó: las líneas alargadas de la pirámide de la punta (del piramidión pequeño) provocan un diagrama secreto en el piso con una estrella octagonal (38min.15seg.). Una estrella octagonal es el símbolo de la diosa sumeriana Inanna, la base de todas las leyendas de Isis (38min.29seg.). La civilización sumeriana fue solo detectada en 1890 (38min.42seg.). Así la ciencia esotérica ha ordenado todo a Isis lo que es en realidad conectado con Inanna (38min.48seg.).
Simbolismo de estrella de octagrama en todo el mundo
-- estrella de la diosa hindú Laksmí (39min.10seg.)
-- el grupo de 8 dioses de Egipto que forman la "ogdóada de Hermopolis" (Amun, Kauket, Amaunet, Hauhet, Naunet, Heh, Nun, Kuk, con el "huevo cósmico" en el centro con el dios solar Ra) (39min.19seg., 1h29min.36seg.).
-- calendario celta (39min.23seg.)
-- gnosticismo valentiano que convierta conceptos de Egipto en conceptos cristianos (39min.29seg.)
-- rueda budista de Dharma (39min.39seg.)
-- octagrama islámico: Rub el Hizb (39min.45seg.)
-- la iglesia ortodoxa también usa estrellas octagramas: Christ Pantocrater (39min.59seg.)
-- la piedra del calendario azteca en México (40min.7seg.)
-- el Vaticano [criminal satanista gay] usa el octágono en su patio y también usa un obelisco como pene en su centro [!] lo que trabaja como reloj solar (40min.23seg.).
En total la estrella de octagrama es un símbolo solar (40min.35seg.).
Monumento de Washington: mediciones de los órganos sexuales femeninos - y la Gran Pirámide de Guiza
La energía femenina del Monumento a Washington es representada con las líneas de un pez "vesica piscis" (40min.46seg.) que representan las piernas de una mujer con su vulva (41min.5seg.). Cuando los círculos de un pez de círculos (vesica piscis) son agrandados hasta al diámetro de la altura del obelisco (sale un diámetro de 555' (pies)) así la Gran Pirámide de Guiza sale exactamente en esa "vulva" (41min.6seg.) con una altura de 481 y 1/11 pies (481'+1/11') (41min.13seg.). Qué coincidencia. El arquitecto del Monumento a Washington debe haber tenido conexiones con los pirámides de Egipto (41min.16seg.).
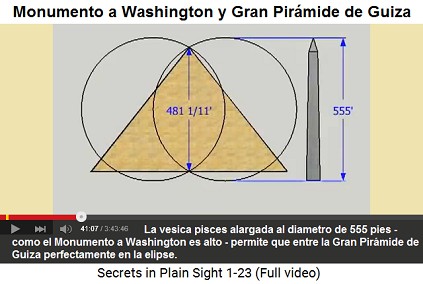 La elipse de pez agrandada del Monumento a Washington a un diámetro de 555' (pies) permite que la Gran Pirámide de Guiza entre perfectamente en esa elipse.
Las proporciones de la Gran Pirámide de Egipto y del obelisco del Monumento a Washington tienen una conexión directa:
-- altura del obelisco del Monumento a Washington (555') = largo inclinado de la Gran Pirámide (555') (41min.20seg.)
-- radio del piramidión proyectado al piso = medio radio de la Gran Pirámide (41min.20seg.)
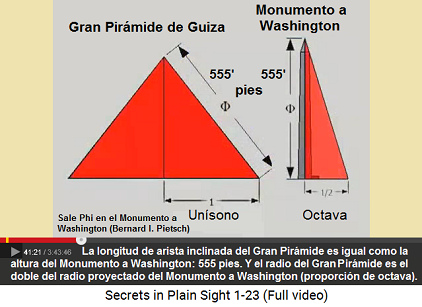 Esquema: el largo inclinado de la Gran Pirámide de Guiza es la altura del Monumento a Washington (555 pies), y el radio de la Gran Pirámide es el doble del radio proyectado del piramidión del Monumento a Washington
Washington DC: el patio trasero de la Casa Blanca es como Stonehenge
El patio trasero de la Casa Blanca tiene la misma forma de "U" como la estructura interior de Stonehenge (41min.43seg.).
 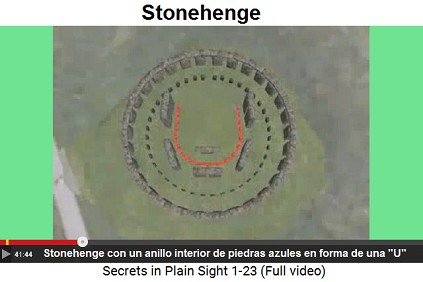 El patio trasero de la Casa Blanca está en forma de una "U" como Stonehenge tiene - Stonehenge con un anillo interior de piedras azules en forma de una "U"
Y los dos triángulos alrededor de la Casa Blanca forman un rectángulo de 5:12 (41min.50seg.). Esas proporciones son las mismas como el rectángulo de piedras de estaciones (41min.53seg.).
  La Casa Blanca con una "U" y triángulos con proporciones 5:12 - Stonehenge con una "U" y con el triángulo de estaciones 5:12 [Conclusión: La Casa Blanca es otro Stonehenge y extraterrestres de Stonehenge están gobernando la Casa Blanca].
Una línea directa de la punta del "Triángulo Federal" de Washington DC al centro de Stonehenge en Inglaterra nos muestra que la línea cruce el Parque Central de Nueva York (42min.9seg.) precisamente en otro ángulo con la proporción de 5:12 (42min.27seg.).
 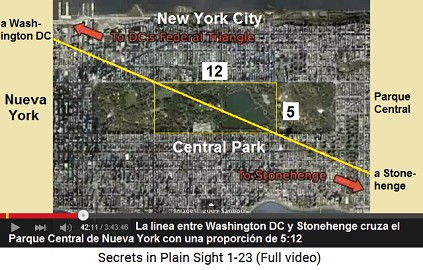 Línea directa de Washington a Stonehenge - La línea entre Washington DC y Stonehenge cruza el Parque Central de Nueva York con una proporción de 5:12 |
|
|
|
|
| Así mismo Leonardo Da Vinci se rodeo de intelectuales de la época entre estos se encuentra el que es considerado EL MEJOR MATEMÁTICO EN SU ÉPOCA, fue un religioso católico.
Luca Pacioli
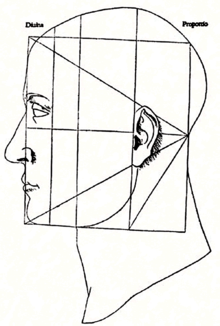
Representación de la cabeza humana acorde con La Divina Proporción (grabado de la edición de 1509, Paganino dei Paganini, Venecia).
Luca Pacioli, de nombre completo Fray Luca Bartolomeo de Pacioli o Luca di Borgo San Sepolcro, cuyo apellido también aparece escrito como Paccioli y Paciolo (Sansepolcro, 1445 - 1517), fue un fraile franciscano y matemático italiano, precursor del cálculo de probabilidades.
Analizó sistemáticamente el método contable de la partida doble usado por los comerciantes venecianos en su obra Summa de arithmetica, geometria, proportioni et proportionalita (Venecia, 1494), que a pesar de su título latino, incluye la primera obra matemática impresa en lengua romance. Es destacable que en la solución de uno de los problemas, utilizara una aproximación logarítmica, un siglo antes que John Napier.1
Su obra más divulgada e influyente es De Divina Proportione (De la Divina Proporción) término relativo a la razón o proporción ligada al denominado número áureo, escrita en Milán entre 1496 y 1498, y que trata también, en su primera parte, de lospolígonos y la perspectiva usada por los pintores del Quattrocento (Compendio Divina Proportione); en su segunda, de las ideas arquitectónicas de Vitruvio (Summa de arithmetica, geometria, proportioni et proportionalita); y en su tercera, de lossólidos platónicos o regulares (De quinque corporibus regularibus). Para ilustrarlo encargó dibujos a Leonardo da Vinci, que en la época formaba parte de la corte milanesa de Ludovico Sforza (il Moro).2
Entre 1477 y 1480 enseñó en la Universidad de Perugia, escribiendo a tal efecto el Tractatus mathematicus ad discipulos perusinos.3 Entre otras obras, escribió también De viribus quantitatis, sobre matemáticas y magia (1496–1508),4 una traducción de los Elementos de Euclides (Geometria, Venecia, 1509) y un manual de ajedrez (De ludo scacchorum).5 6

Sus influencias culturales
Pacioli oscila entre dos concepciones antitéticas de la matemática: una de índole pragmática y otra de índole especulativa e incluso mística; en relación a la segunda no duda en adherirla a las sugestiones místico-mágicas del platonismohumanista originado en la Academia de Marsilio Ficino.
Su obra debe ser entendida acorde con el contexto de la época del Renacimiento italiano. No es un matemático en el sentido epistemológico moderno (como su coetáneo Girolamo Cardano o, más tarde, Johannes Kepler). Pacioli, rememorando aPitágoras, declara que "la ciencia matemática se debe entender como la suma de aritmética, geometría, astrología (entonces confundida aún con la astronomía), música, perspectiva, arquitectura y cosmografía" (esta última en tiempos de Pacioli, aún indiferenciada de la cosmología, topografía y la geografía).La contabilidad moderna
Dentro del "Tractus XI- Particularis de computis et scripturis", nos dejó su legado a través de 36 capítulos (tratado de cuentas de contabilidad usando la partida doble) dando inicio, con eso a la contabilidad moderna.
- Aconseja utilizar cuatro libros: Inventario y Balances, Borrador o Comprobante, Diario y Mayor.
- Define reglas del principio matemático de la partida doble ( o por lo menos su parte fundamental):
1. No hay deudor sin acreedor.
2. La suma que se adeuda a una o varias cuentas ha de ser igual a lo que se abona.
3. Todo el que recibe debe a la persona que da o entrega.
4. Todo valor que ingresa es deudor y todo valor que sale es acreedor.
5. Toda pérdida es deudora y toda ganancia acreedora.
La Suma fue la primera publicación de aritmética y si bien fue él quien lo publicó es posible
que otros estudiosos también hayan hecho aportes a la misma.
http://es.wikipedia.org/wiki/Luca_Pacioli
|
|
|
|
 Primer Primer
 Anterior
12 a 26 de 26
Siguiente Anterior
12 a 26 de 26
Siguiente
 Último
Último

|
|
| |
|
|
©2026 - Gabitos - Todos los derechos reservados | |
|
|

