|
|
General: MARCOS 15:33 (NEXO CON EL HIPERCUBO Y LA CUARTA DIMENSION-MERCURIO-ORION-ISHTAR
Elegir otro panel de mensajes |
|
|
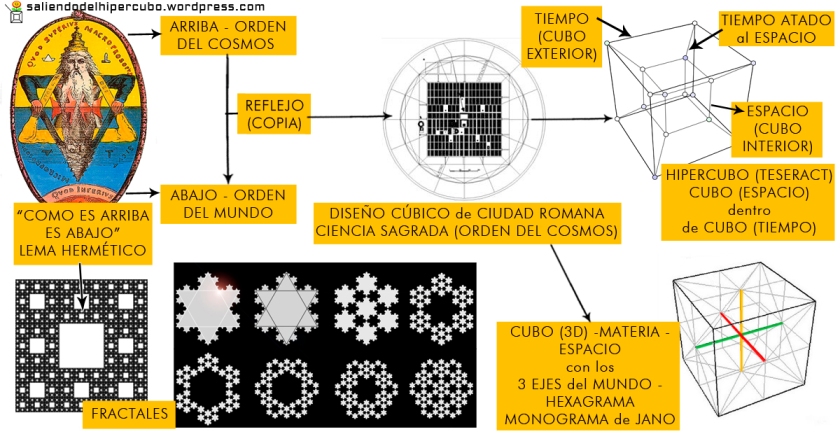
EL HIPERCUBO, LA CUARTA DIMENSION, EL TIEMPO, LA LEY DE LA RELATIVIDAD DE EINSTEIN Y SU NEXO CON MARCOS 15:33
33. Marcos 15:33: Cuando vino la hora SEXTa, hubo tinieblas sobre toda la tierra hasta la hora novena. (CLAVE MERCURIO-ORION-ISHTAR GATE)
Decimal --- Binario --- Cuaternario
00 -------- 0000 ------ 00
01 -------- 0001 ------ 01
02 -------- 0010 ------ 02
03 -------- 0011 ------ 03
04 -------- 0100 ------ 10
05 -------- 0101 ------ 11
06 -------- 0110 ------ 12
07 -------- 0111 ------ 13
08 -------- 1000 ------ 20
09 -------- 1001 ------ 21
10 -------- 1010 ------ 22
11 -------- 1011 ------ 23
12 -------- 1100 ------ 30
13 -------- 1101 ------ 31
14 -------- 1110 ------ 32
15 -------- 1111 ------ 33
Las Triadas "que nos elevan" como acordes (11, 111, 1111) a través de sus ejes o colúmnas pitagóricas. Los puntos de corte de dos dimensiones.
Aquí el el 3, 7 y 15 decimal, o 3, 13, 33 cuaternario. Puntos, entiendo, de la singularidad en tres planos diferentes. O como fusión de contrarios.
3 veces 3 que nos llevan hasta la eclosión del huevo -singularidad fecundativa-.
3 veces 3 como el PLATO (PI-LATO) de Giza. 3 pirámides grandes, 3 pirámides pequeñas (6) y 9 (3+3+3) en total. 369.
http://www.burbuja.info/inmobiliaria/conspiraciones/297306-hilo-oficial-indigomerovingio-148.html
 |
Click para ampliar |
  Lo que me lleva a relacionar esto del 3 veces 3 con los armónicos solfeggio y sus puntos de corte o frecuencias doradas, donde el "dragón se eleva"
|
Click para ampliar |
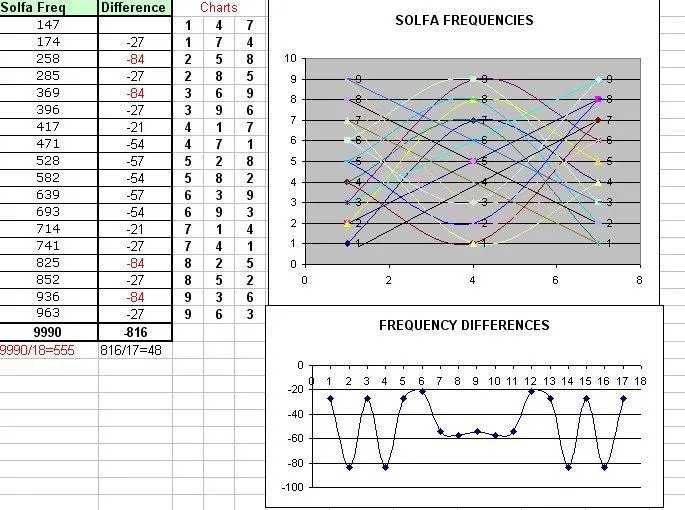 Bettle-Juice, Beetle-Juice, Beetle-Juice.Veo ademas que la suma reducida es 3-6-9.
|
Click para ampliar |
 3 veces 3.
Viene de digitalización de primera semana de curso:
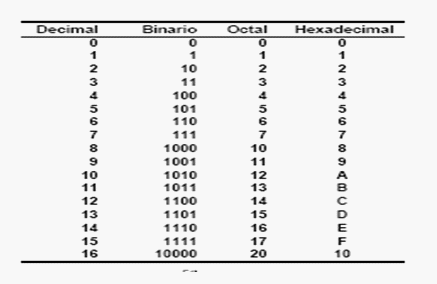
El concepto, que no es nuevo, es que los dieciséis primeros números decimales se pueden mostrar en un nibble binario (medio Byte) resultando 1111 como indicaba IM al representar las coordenadas de los vértices del cubo 4D...
Ahora viene el nuevo apunte...
Que pasa si mostramos esos mismo número decimales en un sistema en base cuatro o cuaternario:
Decimal --- Binario --- Cuaternario
00 -------- 0000 ------ 00
01 -------- 0001 ------ 01
02 -------- 0010 ------ 02
03 -------- 0011 ------ 03
04 -------- 0100 ------ 10
05 -------- 0101 ------ 11
06 -------- 0110 ------ 12
07 -------- 0111 ------ 13
08 -------- 1000 ------ 20
09 -------- 1001 ------ 21
10 -------- 1010 ------ 22
11 -------- 1011 ------ 23
12 -------- 1100 ------ 30
13 -------- 1101 ------ 31
14 -------- 1110 ------ 32
15 -------- 1111 ------ 33
Inquietante... 
¿Esta letra en base cuatro como se podría representar físicamente? Considero que lo mas adecuado sería un tetraedro regular (formado por 4 triángulos equiláteros), el primero de los sólidos platónicos. Donde cada uno de sus cuatro vértices se encuentran a distancias simétricas entre ellas.
Como para representar el 15 decimal (el 33 en base 4) se necesitan dos dígitos en cuaternario, la forma física de integrar ambas letras sería mediante dos tetraedros unidos en que su vórtices continuaran de forma simétrica.
Resumiendo se puede decir, que un hipercubo es lo mismo que lo que se suele representar como Merkaba
...
..
.
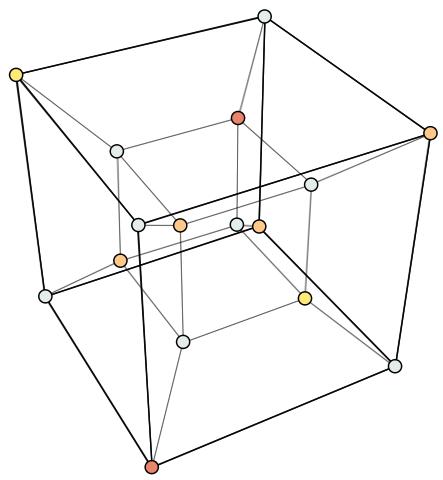
Y que este simbolismo:
Es igual a este:
O al menos que debe representar un concepto muy similar...
|
|
|
|
|
a bit of info : Vladimir Putin Confirms Russian Zombie Radiation Gun
Quote:
| Precise details have not been revealed but previous research has shown that low-frequency waves or beams can affect brain cells, alter psychological states and make it possible to transmit suggestions and commands directly into someone's thoughts. |
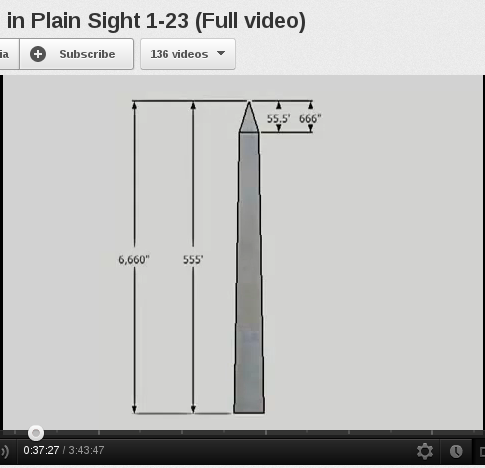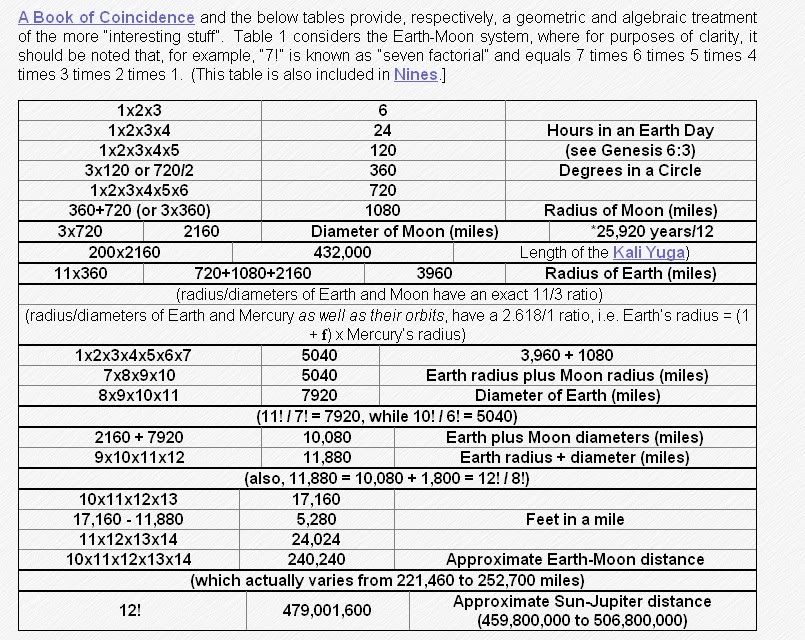Principle of Correspondence ... if we humans can do it ... so can the Celestial Intelligences  ------------------- one more link   Use Harmonic Math on the following table   images from : The Brain is an Advanced Fractal Antenna - Page 10__________________ “Signs and symbols rule the world, not words nor laws.” - Confucius. 
|
|
|
|
|
|
NÚMEROS CÚBICOS.
Los números cúbicos son aquellos que obtenemos al elevar al cubo los sucesivos números naturales:
13 = 1; 23 = 8; 33 = 27; .....
Pero también podemos construir estos números geométricamente,
|
|
|
es.walyou.com
2 Alcancia cubo Rubik
521 × 423 - 24k - jpg |
es.wikipedia.org
El interior de un cubo de
232 × 199 - 28k - jpg |
solostocks.com
Cubo Mágico
500 × 500 - 29k - jpg |
pocoseso.com
del Rubik - Cubo Magico -
450 × 338 - 28k - jpg |
Búsquedas relacionadas con cubo magico
EL MISMO "CUBO MAGICO" ES UN HIPERCUBO (HAY UN CUBO MAS CHICO EN EL CENTRO DEL MISMO)
| Reply |
Message 24 of 24 on the subject |
|
El término cuarta dimensión aparece en diversos contextos como la física, las matemáticas y la ciencia ficción. En cada contexto el significado es diferente:
En física, se hace referencia a la cuarta dimensión al hablar del tiempo, principalmente desde el planteamiento de la Teoría de la Relatividad.
En matemática, el concepto aparece asociado o bien a espacios euclídeos de más de tres dimensiones o, más generalmente, a espacios localmente euclídeos o 4-variedades diferenciables.
Hipercubo de 4 dimensiones espaciales girando, tal como se vería proyectado en el espacio tridimensional.
El interés en las dimensiones más altas alcanzó su clímax entre 1870 y 1920.1 En esos años se convirtió en tema frecuente en la literatura fantástica, el arte e incluso algunas teorías científicas. La cuarta dimensión, entendida como dimensión espacial adicional (no como dimensión temporal, como en la teoría de la relatividad) apareció en las obras literarias de Oscar Wilde, Fiódor Dostoyevski, Marcel Proust, H. G. Wells y Joseph Conrad, inspiró algunas obras musicales de Alexander Scriabin, Edgar Varèse y George Antheil y algunas obras plásticas de Pablo Picasso y Marcel Duchamp influyendo en el desarrollo del cubismo. Incluso personajes tan diversos como el psicólogo William James, la escritora Gertrude Stein o el socialista revolucionario Vladimir Lenin se interesaron en el tema.
Igualmente los matemáticos habían estado interesados en el tema al tratar de generalizar los conceptos de la geometría euclídea tridimensional. El matemático Charles L. Dodgson, que enseñó en la Universidad de Oxford, deleitó a generaciones de escolares escribiendo libros, bajo el pseudónimo de Lewis Carroll, que incorporaban algunas ideas sobre la cuarta dimensión. Desde el punto de vista académico, el estudio general de la geometría de la cuarta dimensión en gran parte resultado de los trabajos de Bernhard Riemann. Charles Howard Hinton, matemático y escritor de ciencia ficción británico, acuñó muchos neologismos para describir elementos en la cuarta dimensión. De acuerdo con el Oxford English Dictionary, fue el primero en emplear la palabra tesseract en su libro Una nueva era del pensamiento. También inventó las palabras “kata” (del griego “abajo”) y “ana” (del griego “arriba”) para describir las dos direcciones opuestas en la cuarta dimensión, equivalentes a derecha-izquierda, arriba-abajo, y adelante-atrás.
Los trabajos matemáticos sobre geometrías multidimensionales y geometrías no euclídeas habían sido considerado por los físicos como simples abstracciones matemáticas hasta que Henri Poincaré probó que el grupo de transformaciones de Lorentz que dejaban invariantes las ecuaciones del electromagnetismo podían ser interpretadas como "rotaciones" en un espacio de cuatro dimensiones. Más tarde, los trabajos de Einstein y la interpretación geométrica de estos por parte de Hermann Minkowski llevaron a la aceptación de la cuarta dimensión como una descripción necesaria para explicar los hechos observados relacionados con el electromagnetismo. Sin embargo, aquí la "cuarta dimensión" no era un lugar separado del espacio tridimensional (como en varias de las obras de ficción de la época) ni tampoco una dimensión espacial análoga a las otras tres dimensiones espaciales, sino una dimensión temporal que sólo puede recorrerse hacia el futuro. En la teoría general de la relatividad el campo gravitatorio es explicado como un efecto geométrico de la curvatura de un espacio-tiempo de cuatro dimensiones.
Más tarde, la teoría de Kaluza-Klein propuso que no sólo el campo gravitatorio podía ser interpretado de forma más sencilla como curvatura de un "espacio" de más de tres dimensiones, sino que si se introducía una nueva dimensión espacial enrollada o «compactificada», también el campo electromagnético podía ser interpretado como un efecto geométrico de la curvatura de dimensiones superiores. Así, la Kaluza proponía una teoría de campo unificado del electromagnetismo y la gravedad en un espacio-tiempo de cinco dimensiones, con una dimensión temporal, tres dimensiones espaciales extendidas y una dimensión espacial «compactificada» adicional, que, debido a su condición de compactificada, no era directamente visible pero su efecto era perceptible en forma de campo electromagnético.
Un ángulo recto se describe como un cuarto de una revolución. La Geometría Cartesiana escoge direcciones ortogonales arbitrariamente a través del espacio, lo que significa que cada dirección está en ángulo recto con las demás. Las 3 dimensiones ortogonales del espacio se conocen como altitud, longitud y latitud. La Cuarta Dimensión por lo tanto es la dirección en el espacio con ángulo recto a las 3 direcciones observables.
Un vector espacial es un conjunto de vectores, los cuales podemos imaginarlos como flechas, que proviene de un simple lugar llamado origen (vectores geométricos), que apuntan a otros lugares.
Un punto es un objeto de cero dimensiones. No tiene extensión en el espacio ni propiedades, como una flecha pero sin longitud. Este vector es llamado el vector cero y es el más simple vector espacial.
Una línea es un objeto unidimensional. Si escogemos un cierto vector distinto a cero en una cierta dirección, este vector tiene cierta longitud definida. Ese vector tiene una cabeza en un cierto punto en espacio y una cola en el origen. Si pensamos en estirar que ese vector así sea dos veces su largo, tres veces, etcétera y uniformemente, tomando todas las longitudes posibles (incluso la longitud cero, conseguir el vector cero), conseguiremos una sola línea con una sola dimensión: La de la longitud. Todos los vectores que describen puntos en esta línea serían paralelos. Aunque para visualizar la línea es necesario que ésta tenga un ancho mínimo, sin embargo, una línea de 1D no la tendría.
Un plano es un objeto de dos dimensiones. Tiene longitud y anchura pero no profundidad - algo como una hoja de papel, o más exactamente algo como las imágenes en un televisor común. El pensamiento en un plano en términos de vectores puede ser un poco más desafiante. Si pensamos en tomar un vector y lo movemos de modo que su cola esté tocando la cabeza del primero y esté formando un vector con su cola en el origen y la cabeza en la cabeza del segundo vector colocado de nuevo, tenemos una manera razonable de hablar de vectores de adición. Si tenemos dos vectores que no sean paralelos, podemos hablar de todos los puntos que podemos alcanzar por o solamente el estirar o ningunos de los vectores, y, agregando estos vectores juntos, estos puntos forman un plano.
El espacio, como lo percibimos, es tridimensional. Podemos pensar en poner una línea junto con un plano. Estas líneas son como un emparedado. Para conseguir a un cierto punto en espacio, podemos imaginarnos el viajar encima de la línea y después el movernos a través del plano al punto. Entonces tenemos tres vectores a pensar alrededor, uno a viajar una cierta distancia encima de la línea y dos para conseguir a un cierto punto en espacio.
Para tres rectas ortogonales en el espacio tridimensional (x, y y z) existe una cuarta, normal al espacio, ortogonal a estas tres rectas, que forma un eje p. ej. w.
El producto vectorial es la determinante de una matriz 4×4, donde una de las filas (o columnas) son los vectores unitarios h, i, j y k y las demás (filas o columnas respectivamente) están formadas por las componentes de tres vectores cuadradimensionales cualesquiera, este producto nos dará un cuarto vector perpendicular a estos tres mismos.
La Geometría euclidiana prevé una mayor variedad de formas para existir que en tres dimensiones. Los poliedros tridimensionales son recintos espaciales hechos de caras de dos dimensiones conectadas, los policronos cuadridimensionales son recintos del espacio cuadridimensional hechos de poliedros tridimensionales. Donde en tres dimensiones, hay exactamente cinco poliedros regulares, o los sólidos platónicos, que pueden existir, seis policronos regulares existen en la cuarta dimensión. Cinco de los seis se pueden interpretar como extensiones naturales de los sólidos platónicos, así como el cubo, un sólido platónico, es una extensión del cuadrado de dos dimensiones. El pentachoron está hecho de 5 tetraedros para las caras y 10 caras triangulares, y es el análogo cuadridimensional del tetraedro. El teseracto, o el hipercubo, se compone de 8 caras cúbicas y de 24 cuadrados, y es el politopo cuadridimensional medido. Los teseractos se doblan, la 16-celdas, son el equivalente del octaedro, pues son ambos politopos de cruz. Los politopos de 120 celdas y los de 600 celdas se doblan de igual modo, y son análogos al dodecaedro y al icosaedro, respectivamente. El de 24 celdas es un policrono regular único y que no tiene ningún equivalente tridimensional. Apenas pues la esfera, o 2-esfera, es una superficie de dos dimensiones curvada compuesta de todos los puntos equidistantes de un punto central dado, en un espacio tridimensional, la 3-esfera, una clase de hiperesfera, es el espacio que contiene todos los puntos equidistantes a un punto central dado, en un espacio cuadridimensional. Cada sección transversal tridimensional de un 3-esfera es un 2-esfera.
La analogía dimensional se usa frecuentemente para comprender el salto de una dimensión (en este caso, la tercera dimensión) a una más alta (cuarta dimensión). La analogía dimensional consiste en resolver un problema en n + 1 dimensiones relacionándolo primero con un problema análogo de (n - 1) dimensión, vale decir, "una dimensión menos". E igualmente debe analizarse el caso de cómo se relaciona el problema en n con el de (n + 1) dimensiones, es decir, "una más".
Edwin Abbott Abbott en su libro Planilandia (Flatland) escribe sobre un "ser cuadrado" que vive en un mundo de dos dimensiones, como la superficie de un pedazo de papel. Este "cuadrado" se enfrenta a experimentos de un ser tridimensional. El ser tridimensional es percibido por el "cuadrado" como un ser aparentemente divino, ya que puede poner y quitar objetos de una caja fuerte sin romperla ni abrirla (moviéndolos a través de su tercera dimensión), ver todo desde de la perspectiva de dos dimensiones sea incluido detrás de las paredes (puesto que ve "sobre" Planilandia), y totalmente invisible para los habitantes de Planilandia, puesto que está "arriba" y una dimensión por arriba de las dos dimensiones en las que el cuadrado está atrapado. No obstante, el ser tridimensional podría manifestarse en el mundo de dos dimensiones, pero sólo parcialmente, si fuera una esfera, aparecería como una secuencia de círculos sucesivos "que cambian de tamaño" (intersecciones de la esfera con el plano de dos dimensiones). Aplicando analogía dimensional, uno puede deducir que el ser cuadridimensional sería capaz de hazañas similares de nuestra perspectiva tridimensional.
Rudy Rucker demuestra esto en su novela "Spaceland", en la cual el protagonista encuentra los seres cuadridimensionales que demuestran tales energías. Un uso útil de la analogía dimensional en visualizar la cuarta dimensión está en la proyección. Una proyección es una manera para representar un objeto (n+1)-dimensional en la n-dimensión. Por ejemplo, las pantallas de computadora son de dos dimensiones, y todas las fotografías de objetos tridimensionales son representadas en dos dimensiones puesto que la información de la tercera dimensión (o de la profundidad) no puede ser representada por la pantalla (si el observador se mueve, aleje o acerque, la imagen no cambiará). En este caso, la profundidad se quita y se substituye por la información indirecta. La retina del ojo es un arsenal de dos dimensiones de receptores pero puede permitir que el cerebro perciba la naturaleza de objetos tridimensionales usando la información indirecta (como la perspectiva, el sombreado, visión binocular, etc.).
La perspectiva del uso de los artistas da profundidad tridimensional a los cuadros de dos dimensiones. Asimismo, los objetos en la cuarta dimensión se pueden proyectar matemáticamente a las familiares tres dimensiones, donde pueden entonces ser examinados más convenientemente. En este caso, la "retina de un ojo cuadridimensional" tendría un arsenal de receptores tridimensionales. El ser hipotético con tal ojo percibiría la naturaleza de objetos cuadridimensionales usando la información indirecta contenida en las imágenes que recibe en su retina. La proyección de la perspectiva a partir de cuatro dimensiones produce efectos similares como en el caso tridimensional, tal como la perspectiva.
Esto agrega "profundidad cuadridimensional" a estos cuadros tridimensionales. La analogía dimensional también ayuda a entender tales proyecciones. Por ejemplo, los objetos de dos dimensiones son limitados por límites unidimensionales: un cuadrado es limitado por cuatro bordes o líneas. Los objetos tridimensionales son limitados por superficies de bidimensionales: un cubo es limitado por 6 cuadrados. Aplicando analogía dimensional, uno puede deducir que un cubo cuadridimensional, conocido como teseracto, es limitado por los volúmenes tridimensionales.
Y de hecho, éste es el caso matemáticamente: el teseracto es limitado por 8 cubos. Saber esto es indispensable para entender cómo interpretar una proyección tridimensional del teseracto. Los límites del teseracto proyectan a los volúmenes en la imagen, superficies no simplemente de dos dimensiones. Esto ayuda a entender las características de dichas dimensiones que de otra manera sólo confundirían. De igual manera, el concepto de sombras puede ayudarnos mejor a entender la teoría de cuatro dimensiones. Si usted proyectara una luz sobre objeto tridimensional, éste proyectaría una sombra de dos dimensiones. Por lo tanto la luz en un objeto de dos dimensiones echaría una sombra unidimensional (en un mundo de dos dimensiones), y la luz en un objeto unidimensional en un mundo unidimensional echaría una sombra cero-dimensional, es decir, un punto de la no-luz. Esta idea se puede utilizar en la otra dirección; la luz en un objeto cuadridimensional proyectaría una sombra tridimensional. Como ejemplo, la sombra de un cubo transparente, proyectaría una sombra sobre el papel, de dos cuadrados, unidos por sus vértices con 4 segmentos.
Semejantemente, si era un cubo cuadridimensional iluminado con luz de 4 dimensiones, su sombra sería la de un cubo tridimensional dentro de otro cubo tridimensional. Siendo tridimensionales podemos solamente ver el mundo con nuestros ojos en dos dimensiones; el ser cuadridimensional consideraría el mundo en tres. Así podría, por ejemplo, ver los seis lados de una caja opaca simultáneamente. No solamente eso; también podría ver lo que hay al interior de la caja, como en Planilandia, en donde la esfera ve objetos en el mundo de dos dimensiones y todo dentro de ellos simultáneamente. Análogo, un espectador cuadridimensional vería todos los puntos en nuestro espacio tridimensional simultáneamente, incluyendo la estructura interna de objetos sólidos y de cosas obscurecidos de nuestro punto de vista.
Albert Einstein en su célebre teoría de 1905 de la relatividad especial habló por primera vez del tiempo como una cuarta dimensión y como algo indispensable para ubicar un objeto en el espacio y en un momento determinado. El tiempo en la teoría de la relatividad no es una dimensión espacial más, ya que fijado un punto del espacio-tiempo éste puede ser no alcanzable desde nuestra posición actual, hecho que difiere de la concepción usual de dimensión espacial. Aunque inicialmente se interpretó el tiempo como una "dimensión" matemática necesaria para ubicar un evento u objeto, en la teoría de la relatividad general el tiempo es tratado como una dimensión geométrica más, aunque los objetos materiales no puedan seguir una trayectoria completamente arbitraria a lo largo del tiempo (como por ejemplo "dar la vuelta" y viajar al pasado). La necesidad del tiempo dentro de la teoría de la relatividad es necesaria por dos motivos:
En primer lugar, los objetos no sólo se mueven a través del espacio sino que también lo hacen a través del tiempo, es decir su coordenada temporal aumenta continuamente, por lo que hubo la necesidad de hablar del tiempo ligado al espacio como la cuarta dimensión (en inglés spacetime, en castellano espacio-tiempo). Además el ritmo de avance en la dimensión temporal depende del estado de movimiento del observador, produciéndose una dilatación temporal efectiva para los observadores más rápidos en relación al tiempo medido por un observador estacionario.
En segundo lugar, el carácter intrínseco del espacio-tiempo y su cuatridimensionalidad requiere un modo conceptualmente diferente de tratar la geometría del universo, puesto que una cuarta dimensión implica un espacio plano (bidimensional) que se curva en la teoría de la relatividad general por la acción de la gravedad de la materia originándose la curvatura del espacio-tiempo.
Finalmente cabe añadir que algunas teorías físicas como la teoría de Kaluza-Klein y las teoría de supercuerdas, en sus varias versiones, añaden a las tres dimensiones físicas espaciales entre 1 y 9 dimensiones espaciales adicionales, de tipo compacto; además de la dimensión temporal.
|
|
|
|
|
|
|
|
|
EL VINO, LA SANTA CENA Y EL GRIAL
|
|
|
|
|
Ancient cultures knew about sacred geometry reflected in nature and derived their individual measures of length from it. Many ancient writings suggest that this knowledge was given to mankind by god(s). The ‘Gods’ of certain cultures could be early post-flood founders a few generations after Noah. In Egypt, building overseers required the Royal Egyptian Cubit to be calibrated against a precision standard at regular intervals. Failure to do so was punishable by death. This extreme respect for the royal cubit indicates an important legacy, like a standard handed down from the ‘Gods’.
According to the “Secrets of the Great Pyramid” (by L. Stecchini) the Egyptian measures of length, originating from at least the 3rd millennium BC, were directly derived from the circumference of the earth with an amazing accuracy. On page 346, his claim is that the Egyptian measurement was equal to 40,075,000 meters, which compared to the International Spheroid of 40,076,596 meters gives an error of 0.004%. No consideration seems to be made to the question of, on purely technical and procedural grounds, how the early Egyptians, in defining their cubit, could have achieved a degree of accuracy that to our current knowledge can only be achieved with very sophisticated equipment and techniques.
Note: Egyptians calculated polar radius as 12,000,000 Royal Cubits (of 0.525 m per cubit) which is equivalent of 6300 km (modern value for the polar radius of the Earth is 6,357km)
The Sacred Cubit (aka Royal Cubit) was used in constructing buildings and monuments and in surveying in ancient Egypt. Royal Cubit consists of 28 units, digits ( 7 palms of 4 digits). The names of divisions of royal cubit may suggest anatomical origin, however the division numbers indicate astronomical origin of the cubit (7 days per week, 28 days lunar calendar, 4 weeks per lunar month)…
Note: Here is an interesting connection between modern and ancient units of length with astronomy and geodesy: 1 foot = 12 inches, 1 mile = 5280 feet = 63,360 inches = 4800 Sumerian Feet = 3200 Sumerian Cubits.
There is great confusion today concerning metrology, the history of measurement systems around the world. Beyond the child’s tales of the “foot” deriving from some king’s foot, measurement was actually part of a sacred system of knowledge established in prehistory and based on timeless truths seen in the harmony of the cosmos. Standards of measure were everywhere framed upon never-changing principles of number, in particular, the interplay of natural tension between ten and twelve, and the dimensions of the turning Earth. Except for the survival of the English system in the U.S., most other traditional systems of measurement worldwide have succumbed to the “easy” and modern, but inferior “metric” system, which uses only ten, is divorced from nature and the human scale, and requires its users to conform to the measuring tools themselves, not to the nature of the objects measured, as was traditionally done.
The Cosmological Diagram (The New Jerusalem Diagram)
The Sacred Geometric Community has fallen short of the grand prize, the New Jerusalem and her fullness of purpose, they have at least seen, especially through the apostolic efforts of John Michell, the suburbs of the Holy City and from this afar view have come imminently close to her profound and universal meaning; and certainly by framing their quests for universal understanding and sustainable social systems in terms of the Celestial City (or as in Plato’s case, Magnesia). Their approach to the City Whose Builder and Maker is God (even though that “god” is NOT the One of revelation and authority held by their antagonists amongst the aforesaid monotheists), as we all, is seen through a glass darkly but, nevertheless, they are searching to unlock the mystery of the New Jerusalem and to confirm their findings through geodetic discovery.
Another version of the NJ Diagram is Magical Seal of Solomon.
In Medieval Jewish, Christian and Islamic legends, the Seal of Solomon was a magical signet ring said to have been possessed by King Solomon, which variously gave him the power to command demons, genies (or jinni), or to speak with animals. In some versions the seal was made of brass and iron, carved with the Name of God, and set with four jewels. In later versions the ring simply bore the symbol now called the Star of David (hexagram), often within a circle, usually with the two triangles interlaced rather than intersecting.
To them the “geometric construction” of the New Jerusalem presents cosmological realities which govern the universe – a universe numerically understood far more by the “ancients” who have left us a testament in their objects and writings to these realities whereby John’s vision of the Holy City is the culmination of all their most vivid aspirations; to wit, the elaborate geometric configurations from the New Jerusalem Diagram to intriguing planetary measurements of circles, squares, triangles, polygons of all sorts which provide immediate connectivity between earth and heaven’s realms – as well as those earthly objects of antiquity which replicate the heavenly dimensions of Paradise, and all within the context, preservation and accuracies of antiquity:
“Another relic of the archaic tradition that produced these divisions of time is our present system of measurement by units of feet, furlongs, and miles, with the acre as the unit of land measuring. Those measures, which are still found the most convenient today, were canonized and held sacred, because not only do they relate both to the human and to the astronomical scales, expressing the unity between macrocosm and microcosm, but they bring out the same numbers in the dimensions of the solar system as were given to the units of time.” — Dimensions of Paradise, Michell, p. 117.
One of the foremost metrologists of Teotihuacán is, without equivocation, Dr. Hugh Harleston Jr., who during the late 1960s and 1970s measured this “ritual city” from a “…unified geometrical composition whose intervals are clearly defined, and Harleston was soon able to establish the basic unit of measure in its dimensions. This proved to be a unit of 1.0594 meters, which Harleston called the Standard Teotihuacán Unit (STU) or Hunab after the Mayan word, adopted by the Aztecs, for Measure. He also recognized the geodetic significance of that unit: 1.0594063 meters is equivalent to the ‘Jewish rod’ of 3.4757485 ft., the same unit which represents the width of the Stonehenge lintels, a six-millionth part of the earth’s polar radius and one part in 37,800,000 of its mean circumference.” (Ref. The New View Over Atlantis, Dr. John Michell, 1995, p. 131).
Also: “Harleston says of Teotihuacan’s builders: ‘When they draw a line, they’re telling you an area. When they draw an area, they’re telling you a volume. When they put volume, they’re telling you time.”
Geodesy and geodetic placement of “sacred sites” of ancient origins has long been affirmatively suspect – especially, the Great Pyramid of Giza. Geodesy involves a fundamental understanding of plane or solid geometry, astronomy relative to latitude and longitude with latitude of more recent vintage since ships-clock (cir. 1540) came into vogue. These geodetic or geometric relationships both on earth and in the heavens are a frequent haunt of pagans and occultists and of novel interest to science – though science with its unfortunate proliferation of skeptic is apt to go off into “metric tangents” and miss out on all the “fun!” “For quite some time researchers have been documenting the astronomical alignments of ancient archaeological and megalithic stone sites all over the world. But discovery of their geodesic alignment has been more recent. Geodesy refers to the theory and practice of surveying to determine the position of specific points on Earth’s surface. It is distinguished from plane surveying in that it deals with areas whose dimensions are so great that the curvature of the Earth must be taken into account. Geometric geodesy involves the creation of a mathematical model of Earth, while physical geodesy studies Earth’s gravity field. The discovery of the precise alignment of Mayan sites along the 90th parallel is significant because it demonstrates that the Maya were aware of Earth’s curvature and knew the advanced formulas used in geodesy.
Note: Carl Munck, archaeocryptographer, introduces an ancient Pyramid Matrix, in which ancient monuments – across the globe – encode their exact positions with respect to latitude and longitude. The science of decoding these monuments is called archaeocryptography. For latitude, ancient monuments were referenced to the same (modern) equator. For longitude, these monuments were referenced to a former Giza, Egypt Prime Meridian – discovered by Munck – that ran from pole to pole across the Great Pyramid.
PS1 The Forgotten Harmonical Science of the Bible
Note: The following segment is from “The forgotten harmonical science of the Bible” by Ernest G. McClain
“…but thou hast ordered all things in measure and number and weight” — Wisdom of Solomon 11:20 (1611 King James Bible)
Biblical creation “by measure, number and weight” required God to possess a fluency in arithmetic not always shared by the faithful. And so Bible arithmetic of the first millennium BC eventually became incomprehensible.
Today much of the astronomy, arithmetic, and music attributed to Classical Greece is documented to Semitic Babylon in the second millennium B.C. Mesopotamian fluency in calculation–in the age of Abraham, Isaac, and Jacob–already was 3000 years ahead of 16th century AD Europe. Babylonian exile in the sixth century BC made accessible to the Jews anything not already known.
With help of Philo of Alexandria I am reading Divine prescience as pre-scientific musical insight encoded in tribal mythology. Biblical emphasis on twelve sons as eponymous ancestors of twelve tribes who build an altar of twelve stones concerns twelve idealized “boundary markers” in a cyclic octave needed for Davidic musicology. The pattern was long symbolized in the concentric circles of the Babylonian astrolabe, adjusted monthly to correlate the watches with the varying lengths of day and night. Figure 2 strips all star data from van der Waerden’s reconstruction, and converts his base-60 water-clock weights (for full watches in the outer circle, and half and quarter watches in the inner circles) to base 10 arithmetic.
The astrolabe’s naked geometry and simple arithmetical doubling expose the idealist mind set which guided the evolution of Chaldaean sciences — converted to priestly ritual by Jewish ingenuity. Twelve ideal months of 30 fictitious days were superimposed on the heavens, and the ratio of longest night to shortest day, known to be about 3:2, was computed as 2:1, so that only music offered a “manipulable” example which conformed to these rounded measures.
Concentric circles anticipate Ezekiel’s “wheel in a wheel” as the throne of heaven. Within each circle maxima and minima water clock weights of 2:1 anticipate the ratio of cyclic octaves. But equal weight differences between successive months (reversing at the solstices in months III and IX) had to give way to proportional differences between successive semitones when this geometry was applied to music. Rational tonal arithmetic, cleverly mimed by Ezekiel, could anticipate this conceptual equality only via a slight but cumulative excess or deficiency, for in a cyclic octave of ratio 1:2 all equal divisions are defined by irrationals. Thus the Holy Land of a spiritual Israel had to be conquered conceptually in intricate warfare between the excess of primordial “giants” (products of 3) and the deficiency of human “weaklings” (products of 5) among rational numbers, and “weaklings” won only with Divine help in circumventing the lack of real number. Bible narrative brilliantly allegorizes every aspect of Diophantine approximation to modern Equal Temperament, and it does so with exhausting respect for numerical detail–making the Bible a priceless repository of tuning lore and its elementary number theory. The “unhewn” stones of Jewish altars are integers, meaning the natural or counting numbers to which harmonical theory normally was restricted, although its calculation demanded great fluency with reciprocal fractions. From the perspective of any reference pitch all integers except 2n necessarily “sinned” by “missing the mark” to some degree because octave doubling imposed, a priori, a universal matrix (“womb”) tied to integral powers of 2. Problems arose immediately with division into 2 equal parts (requiring the square root of 2) and 3 parts (requiring the cube root of 2).
Sensory intuition always fails at some level of arithmetical subtlety where least noticeable differences create a Platonic “no man’s land” of uncertainty. Greek, Jewish, and Chinese cultures are unanimous in accepting the comma of 80:81 as its convenient normative value. It is the difference between a “giant” wholetone of 8:9 (worth 204 cents in modern logarithmic measure) and a “human weakling” of 9:10 (worth only 190). They are approximations to the sixth root of 2 worth 200 cents, the value necessary to divide an octave 1:2 into six equal parts. How Davidic tuning theory reconciles this conflict becomes the central focus of Bible allegory And in the sixth century BC only God could have solved this problem numerically–although any geometer could map results to his own satisfaction for the astrolabe pointed the way.
For musician/philosophers of Philo’s temperament, tuning theory may always have been a contest in the soul between the potential tyranny of masculine intellection, considered mankind’s very highest power, and the relative benevolence of our feminine sensorium, where least noticeable differences create some measure of perceptual tolerance. Wisdom required a congenial mating between our own masculine concepts and feminine percepts, and sometimes rewarded it with the experience of transcendent beauty in “out of the body” adventures like Philo enjoyed when listening to the antiphonal singing of segregated sexes in his Alexandrine synagogue. I am trying here to articulate Bible harmonics in Philo’s spirit while paying closer attention to its computational logic.
http://blog.world-mysteries.com/science/the-language-of-god/
|
|
|
|
|
Sólido de Kepler-Poinsot
Los sólidos de Kepler-Poinsot con sus símbolos de Schläfli.
Un sólido de Kepler (también llamado sólido de Kepler-Poinsot) es un poliedro regular no convexo, cuyas caras son todas polígonos regulares y que tiene en todos sus vértices el mismo número de caras concurrentes (compárese con los sólidos platónicos).
Existen sólo cuatro tipos, con las denominaciones siguientes:
Las caras están solo parcialmente en la superficie del sólido, y las partes expuestas están sólo conectadas en puntos (si están conectadas de algún modo). Si las partes se cuentan como caras separadas, el sólido deja de ser regular.
Características
Un sólido de Kepler cubre su esfera circunscrita más de una vez (con una esfera interior y otra exterior), con los centros de las caras como puntos direccionales en los sólidos que tienen caras en forma de pentagrama, mientras que en los otros son los vértices los que cumplen esa función. Por esta razón, no son necesariamente equivalentes topológicos de la esfera como lo son los sólidos platónicos, y en particular la característica de Euler V − E + F = 2 se verifica solamente para el Gran dodecaedro estrellado y para el Gran icosaedro.
Esto dependerá de cómo se observe el poliedro. Considérese, por ejemplo, el pequeño dodecaedro estrellado.1 Consiste en un dodecaedro con una pirámide pentagonal en cada una de sus 12 caras. En consecuencia, las 12 caras se extienden a pentagramas con el pentágono central dentro del sólido. La parte externa de cada cara consiste en cinco triángulos conectados por sólo cinco puntos. Si se cuentan separadamente, hay 60 caras (pero estas son triángulos isósceles que no son polígonos regulares, en cuyo caso seria un pentaquisdodecaedro). De modo similar, cada lado puede ser contado como tres, pero entonces los habrá de dos tipos. Igualmente, con los "cinco puntos" antes mencionados: en total habrá 20 puntos que pueden contarse como vértices, por lo que habrá un total de 32 vértices (otra vez, de dos tipos). Ahora la ecuación de Euler se verifica: 60 - 90 + 32 = 2.
Tipos
Hay cuatro sólidos de Kepler distintos:
Los dos primeros son estrellamientos, es decir, sus caras son convexas. Los otros dos tienen caras cóncavas, pero cada par de caras que se encuentra en un vértice de hecho lo hace en dos.
Historia
Mosaico del suelo en la basílica de San Marcos, a veces atribuido a Paolo Uccello.
La mayoría de los poliedros de Kepler-Poinsot, si no todos, eran ya conocidos de una forma u otra antes de Kepler. Un pequeño dodecaedro estrellado aparece en una tarsia de mármol (panel de incrustaciones) en el suelo de la basílica de San Marcos de Venecia, Italia. Data del siglo XV y, a veces se atribuye a Paolo Uccello. Wenzel Jamnitzer, en su obra Perspectiva corporum regularium (Perspectivas de los sólidos regulares), un libro de grabados en madera publicado en el siglo XVI, representa el gran dodecaedro y el gran dodecaedro estrellado.2 Se desprende de la disposición general del libro que consideraba solamente los cinco sólidos platónicos como regulares, y no comprendía la naturaleza periódica de sus grandes dodecaedros.
El pequeño y gran dodecaedro estrellado, a veces llamados poliedros de Kepler, fueron reconocidos por primera vez como regulares por Johannes Kepler en 1619, cuando notó que los dodecaedros estrellados (tanto el grande como el pequeño) se componían de dodecaedros "ocultos" (con caras pentagonales) que tienen caras compuestas de triángulos, tomando la apariencia de estrellas estilizadas. Los obtuvo por estelación del dodecaedro regular convexo, por primera vez, tratándolo como una superficie en lugar de un sólido. Se dio cuenta de que extendiendo los bordes o caras del dodecaedro convexo hasta que se encontrasen de nuevo, se podían obtener pentágonos estrellados. De esta manera construyó los dos dodecaedros estrellados, cada uno con la región convexa central de cada cara "oculta" en el interior, sólo con los brazos triangulares visibles. El paso final de Kepler fue reconocer que estos poliedros se ajustaban a la definición de regularidad, aunque fueran cóncavos en lugar de convexos, como sí lo eran los tradicionales sólidos platónicos.
En 1809, Louis Poinsot redescubrió las figuras de Kepler, mediante el ensamblaje de pentágonos estrellados alrededor de cada vértice. También montó polígonos convexos alrededor de los vértices de las estrellas para descubrir dos estrellas más regulares, el gran icosaedro y el gran dodecaedro. Por ello, algunos llaman a estos dos los poliedros de Poinsot. Poinsot no sabía si había descubierto todos los poliedros regulares estrellados.
Tres años más tarde, Augustin Cauchy demostró que la lista por estelación de los sólidos platónicos estaba completa, y casi medio siglo después, en 1858, Joseph Louis François Bertrandproporcionó una prueba más elegante por facetado de ellas.
Al año siguiente, Arthur Cayley dio a los poliedros de Kepler–Poinsot los nombres por los que generalmente conocidos hoy.
Unos cien años más tarde, John Conway desarrolló una terminología sistemática para las estelaciones hasta un máximo de cuatro dimensiones. Dentro de este esquema, sugirió nombres ligeramente modificados para dos de los poliedros regulares estrellados. Los nombres de Conway han sido considerados de utilidad, pero no han sido ampliamente adoptados.
| Nombre de Cayley |
pequeño dodecaedro estrellado |
gran dodecaedro |
gran dodecaedro estrellado |
gran icosaedro |
| Nombre de Conway |
dodecaedro estrellado |
gran dodecaedro (sin cambio) |
dodecaedro grande estrellado |
gran icosaedro (sin cambio) |
https://es.wikipedia.org/wiki/S%C3%B3lido_de_Kepler-Poinsot |
|
|
 First Previous 2 to 5 of 5 Next  Last |
|
|
Posted in Azulejos-Mosaicos, Italia, Templo with tags Poliedros on 7 junio 2012 by angelrequena
Hace tiempo hablamos del conocido pequeño dodecaedro estrellado del pavimento de la puerta de salida derecha del duomo de San Marcos. No es el único de la catedral veneciana: apenas visible para la visita ordinaria hay otro más pequeño, justo debajo del iconostasio en su centro, en lugar preferente y en línea con el altar.
Si se entra hacia la Pala de Oro puede verse una mancha central en la lejanía pero casi sin distinguirse. En mi última visita tuve la gran suerte de encontrar un ordenanza amable que encendía las luces a un grupo concertado que me permitió verlo y fotografiarlo. No desmerece de su hermano mayor, si cabe revela mayor virtuosismo y ostentación del dominio de la perspectiva matemática.
Hay cuatro sólidos regulares cóncavos, los dos de Poinsot y los dos de Kepler. Venecia nos ofrece los dos de Kepler en San Pantaleone y uno en San Marcos pero en dos lugares, uno alejado para despedirse del templo y otro en el lugar más destacado: la entrada central al recinto más sagrado.
El dodecaedro estrellado de la puerta (abajo) solo tiene una corona de taracea marmórea complementaria mientras que el del iconostasio (arriba) tiene tres.
3 Comments »
https://mateturismo.wordpress.com/tag/poliedros/page/7/
|
|
|
|
|
|
|
|
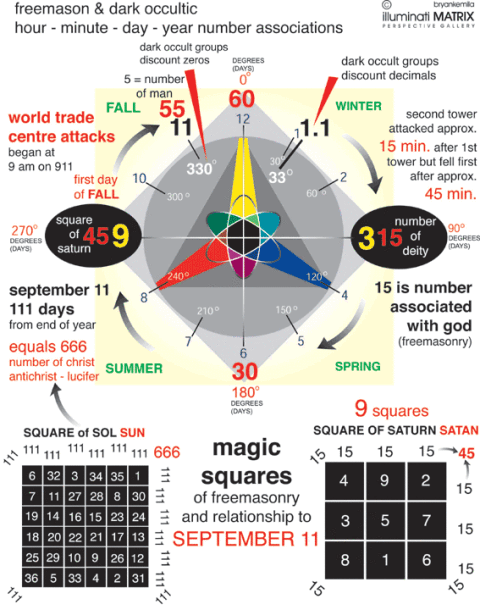
¿COMO EXPLICAS EL NEXO 911 CON EL DIA DE MARIA MAGDALENA EN EL MARCO A LA INDEPENDENCIA DE EEUU EN FILADELFIA?
11/9/2001-11/9/2005=1461 DIAS
11/9/2005-22/7/2006=315 DIAS
1461+315=1776
EL 4/7/1776=INDEPENDENCIA DE EEUU EN FILADELFIA
En aquel tiempo, respondiendo Jesús, dijo:
Te alabo, Padre, Señor del cielo y de la tierra,
que hayas escondido estas cosas (la Gnosis, la Sabiduría Oculta)
de los sabios (de los eruditos) y de los entendidos, (de los intelectuales)
y las hayas revelado á los niños. (A los Iniciados). Así, Padre, pues que así agradó en tus ojos."
(Mateo 11: 25-26).
EL PATRON KAVALISTICO DE LA INDEPENDENCIA DE LOS ESTADOS UNIDOS ESTA TOTALMENTE INTERRELACIONADO CON LAS BODAS DE CANA, EN EL CONTEXTO A QUE LA MISMA NO FUE SOLAMENTE EN UN TERCER DIA ( JUAN 2:1), SINO QUE TAMBIEN EN UN SEPTIMO DIA (JUAN 1:29,35,42 Y JUAN 2:1). DE ALLI SALE EL MONSTRUSO NUMERO 37.
1776=48*37
666=37*18
37*18=666
37*48=1776 (AÑO DE LA INDEPENDENCIA DE EEUU)
LA MISMA TORRE ES UN SIMBOLO FALICO CON FUERTE CONNOTACION SEXUAL
|
|
|
|
|
EL MASONICO "SECRETO MASONICO" DETRAS DE LA MANZANA (EN EL LIBRO DE JOB) /STEVE JOBS, CREADOR DE APPLE
drjudywood.com
The WTC twin towers towering
800 × 600 - 84k - jpg |
en.wikipedia.org
to the World Trade Center,
4256 × 3426 - 12407k - jpg |
Job
25:1 Respondió Bildad suhita, y dijo:
25:2 El señorío y el temor están con él; El hace paz en sus alturas.
25:3 ¿Tienen sus ejércitos número? ¿Sobre quién no está su luz?
25:4 ¿Cómo, pues, se justificará el hombre para con Dios? ¿Y cómo será limpio el que nace de mujer?
25:5 He aquí que ni aun la misma luna será resplandeciente, Ni las estrellas son limpias delante de sus ojos;
25:6 ¿Cuánto menos el hombre, que es un gusano, Y el hijo de hombre, también gusano?
agujero blanco=hombre=boaz
agujero negro=mujer=jachin
salmo 119 (alfa y el omega)
entre los mismos hay un obvio "agujero de gusano"
el hijo, es el OBVIO "AGUJERO DE GUSANO"
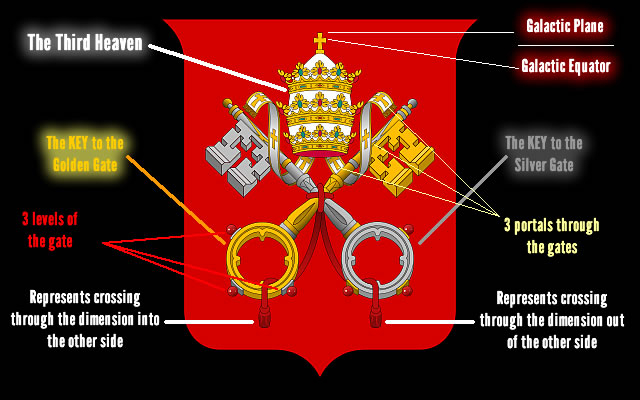
LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
|
|
|
|
|
|
|
22/7=3.14=PI
12 PUNTOS EN SU CIRCUNFERENCIA=RELOJ=SANTA CENA
LONGITUD CIRCUNFERENCIA=PIxDIAMETRO
 |
|
|
|
|
|
|
|
|
|
|
REPRODUCCION DE LOS CONEJOS EN FUNCION A LA SERIE DE FIBONACCI, INCLUSO DEL RELOJ Y DE LA MISMA SANTA CENA (MISMA MANZANA)
 
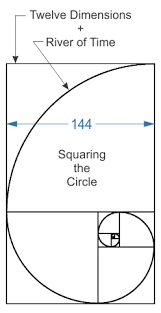
Apocalipsis 21
1. Vi un cielo nuevo y una tierra nueva; porque el primer cielo y la primera tierra pasaron, y el mar ya no existía más.
2. Y yo Juan vi la santa ciudad, la nueva Jerusalén, descender del cielo, de Dios, dispuesta como una esposa ataviada para su marido.
3. Y oí una gran voz del cielo que decía: He aquí el tabernáculo de Dios con los hombres, y él morará con ellos; y ellos serán su pueblo, y Dios mismo estará con ellos como su Dios.
4. Enjugará Dios toda lágrima de los ojos de ellos; y ya no habrá muerte, ni habrá más llanto, ni clamor, ni dolor; porque las primeras cosas pasaron.
5. Y el que estaba sentado en el trono dijo: He aquí, yo hago nuevas todas las cosas. Y me dijo: Escribe; porque estas palabras son fieles y verdaderas.
6. Y me dijo: Hecho está. Yo soy el Alfa y la Omega, el principio y el fin. Al que tuviere sed, yo le daré gratuitamente de la fuente del agua de la vida. (911 O SALMO 119)
7. El que venciere heredará todas las cosas, y yo seré su Dios, y él será mi hijo.
8. Pero los cobardes e incrédulos, los abominables y homicidas, los fornicarios y hechiceros, los idólatras y todos los mentirosos tendrán su parte en el lago que arde con fuego y azufre, que es la muerte segunda.
9. Vino entonces a mí uno de los siete ángeles que tenían las siete copas llenas de las siete plagas postreras, y habló conmigo, diciendo: Ven acá, yo te mostraré la desposada, la esposa del Cordero.
10. Y me llevó en el Espíritu a un monte grande y alto, y me mostró la gran ciudad santa de Jerusalén, que descendía del cielo, de Dios,
11. teniendo la gloria de Dios. Y su fulgor era semejante al de una piedra preciosísima, como piedra de jaspe, diáfana como el cristal.
12. Tenía un muro grande y alto con doce puertas; y en las puertas, doce ángeles, y nombres inscritos, que son los de las doce tribus de los hijos de Israel; (EL MISMO RELOJ, O SANTA CENA O LA MANZANA, LA TRASLACION EN EL TIEMPO)
13. al oriente tres puertas; al norte tres puertas; al sur tres puertas; al occidente tres puertas.
14. Y el muro de la ciudad tenía doce cimientos, y sobre ellos los doce nombres de los doce apóstoles del Cordero.
15. El que hablaba conmigo tenía una caña de medir, de oro, para medir la ciudad, sus puertas y su muro.
16. La ciudad se halla establecida en cuadro, y su longitud es igual a su anchura; y él midió la ciudad con la caña, doce mil estadios; la longitud, la altura y la anchura de ella son iguales. (CUBO=ESPACIO/TIEMPO)
17. Y midió su muro, ciento cuarenta y cuatro codos, de medida de hombre, la cual es de ángel. (EL NEXO DE LA MANZANA, EL PENTAGONO, LA NUEVA JERUSALEN, EL CASTILLO SAN ANGELO DEL VATICANO E INCLUSO EL MISMO PENTAGONO DE WASHINGTON D.C. ES OBVIO EL NEXO DEL RELOJ CON LA MANZANA)
18. El material de su muro era de jaspe; pero la ciudad era de oro puro, semejante al vidrio limpio;
19. y los cimientos del muro de la ciudad estaban adornados con toda piedra preciosa. El primer cimiento era jaspe; el segundo, zafiro; el tercero, ágata; el cuarto, esmeralda;
20. el quinto, ónice; el sexto, cornalina; el séptimo, crisólito; el octavo, berilo; el noveno, topacio; el décimo, crisopraso; el undécimo, jacinto; el duodécimo, amatista.
21. Las doce puertas eran doce perlas; cada una de las puertas era una perla. Y la calle de la ciudad era de oro puro, transparente como vidrio.
22. Y no vi en ella templo; porque el Señor Dios Todopoderoso es el templo de ella, y el Cordero.
23. La ciudad no tiene necesidad de sol ni de luna que brillen en ella; porque la gloria de Dios la ilumina, y el Cordero es su lumbrera. (PROVERBIOS 25:11, OSEA LA MISMA MANZANA, OSEA UNA REFERENCIA AL SOL/ORO/HOMBRE Y LUNA/PLATA/MUJER, OSEA EL MISMO SUEÑO DE JOSE DE GENESIS 37)
24. Y las naciones que hubieren sido salvas andarán a la luz de ella; y los reyes de la tierra traerán su gloria y honor a ella.
25. Sus puertas nunca serán cerradas de día, pues allí no habrá noche.
26. Y llevarán la gloria y la honra de las naciones a ella.
27. No entrará en ella ninguna cosa inmunda, o que hace abominación y mentira, sino solamente los que están inscritos en el libro de la vida del Cordero.
|
|
|
 Primer
Anterior
109 a 123 de 138
Siguiente
Último
|
|
| |
|
|
©2024 - Gabitos - Todos los derechos reservados | |
|
|
