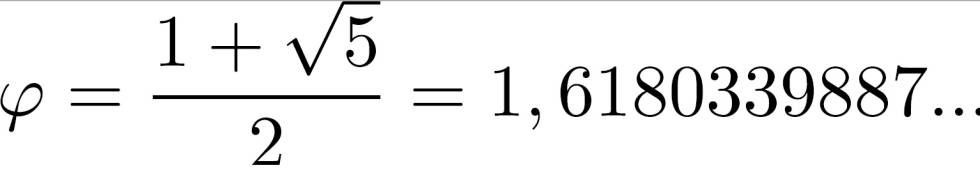|
|
 the Apple
|
|
|
|
|
 the Apple
|
|
|
|
|
7 jun. 2018 - Subido por AGENCIA EFE
Pamplona, 7 jun (EFE) (Imágenes: Javier Rodrigo).- Sophia, la robot humanoide más avanzada del mundo ...
8 abr. 2018
La robot Sophia prefiere entrevistar antes que ser entrevistada. A la primera oportunidad que tiene aprovecha ...
12 feb. 2018 - Subido por Dot CSV
Sophia es la creación de Hanson Robotics, un fenómeno mediático y un símbolo de la nueva revolución de la ...
8 abr. 2018 - Subido por EL PAIS
Como parte de los eventos del 'Talend Land' de Jalisco (México) el robot Sophía tuvo una entrevista en ...
5 sept. 2018 - Subido por Prensa Libre tv
GUATEMALA. En la presentación del Tigo Business 2018, el atractivo principal fue la robot humanoide Sophia ...
10 dic. 2017 - Subido por El Futuro Es Apasionante
Entra en nuestra web: https://elfuturoesapasionante.elpais.com Suscríbete a nuestro canal de youtube: http://bit ...
4 jul. 2019 - Subido por El Hormiguero
Durante la visita de Álvaro Morte y Úrsula Corberó, recibimos a Sophia, un robot humanoide que nos ...
31 jul. 2018 - Subido por Universidad Pontificia Bolivariana - UPB
David Hanson, fundador de Hanson Robotics y creador del famoso robot Sophia, fue uno de los invitados ...
31 jul. 2018 - Subido por EL TIEMPO
"Mi meta no es convertirme en humano o reemplazar a alguien, me siento orgullosa de ser robot, soy mi ...
|
|
|
|
|
BABILONIA LA RAMERA ES UNA MUJER Y ES LA MISMA BESTIA
BABILONIA LA RAMERA ES UNA MUJER Y ES LA MISMA BESTIA
PARA NO CREER PERO ESTO ES ASI. LA RELACION DEL DINERO / MONEY / MOON / CON LA LUNA EN EL CONTEXTO A LA TRANSFIGURACION EN EL MONTE HERMON / MON / LUNA EN LA TRIBU DE DAN / DINERO / SERPIENTE. TODO ES UN NEXO CON LA TRANSFIGURACION DEL SEÑOR. DINERO ES TIEMPO MISMO.
ES OBVIO EL NEXO DE LA SERPIENTE CON LA MUJER
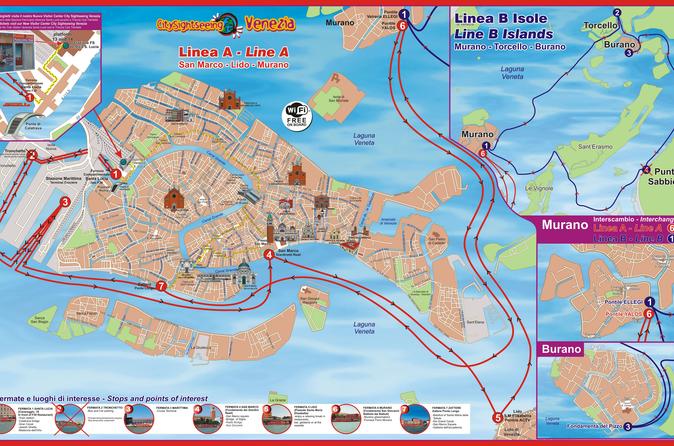
NOTEN EL NEXO DE DAN, CON LA SERPIENTE (VENECIA) Y EL CABALLO (PLAZA SAN MARCOS)
7. Génesis 49:17 Será Dan SERPIENTE junto al camino, Víbora junto a la senda, Que muerde los talones del caballo, Y hace caer hacia atrás al jinete.
 1200 1200
|
|
|
|
|
Fibonacci 24 Repeating Pattern
May 15, 2012 by Gary Meisner
The Fibonacci sequence has a pattern that repeats every 24 numbers.
Numeric reduction is a technique used in analysis of numbers in which all the digits of a number are added together until only one digit remains. As an example, the numeric reduction of 256 is 4 because 2+5+6=13 and 1+3=4.
Applying numeric reduction to the Fibonacci series produces an infinite series of 24 repeating digits:
1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9
If you take the first 12 digits and add them to the second twelve digits and apply numeric reduction to the result, you find that they all have a value of 9.
| 1st 12 numbers |
1 |
1 |
2 |
3 |
5 |
8 |
4 |
3 |
7 |
1 |
8 |
9 |
| 2nd 12 numbers |
8 |
8 |
7 |
6 |
4 |
1 |
5 |
6 |
2 |
8 |
1 |
9 |
| Numeric reduction – Add rows 1 and 2 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
18 |
| Final numeric reduction – Add digits of result |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
This pattern was contributed both by Joseph Turbeville and then again by a mathematician by the name of Jain.
We would expect a pattern to exist in the Fibonacci series since each number in the series encodes the sum of the previous two. What’s not quite so obvious is why this pattern should repeat every 24 numbers or why the first and last half of the series should all add to 9.
For those of you from the “Show Me” state, this pattern of 24 digits is demonstrated in the numeric reduction of the first 73 numbers of the Fibonacci series, as shown below:
|
Fibonacci Number
|
Numeric reduction by adding digits |
| 1st Level |
2nd Level |
Final Level |
| Example: 2,584 |
2+5+8+4=19 |
1+9=10 |
1+0=1 |
| 0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
| 2 |
2 |
2 |
2 |
| 3 |
3 |
3 |
3 |
| 5 |
5 |
5 |
5 |
| 8 |
8 |
8 |
8 |
| 13 |
4 |
4 |
4 |
| 21 |
3 |
3 |
3 |
| 34 |
7 |
7 |
7 |
| 55 |
10 |
1 |
1 |
| 89 |
17 |
8 |
8 |
| 144 |
9 |
9 |
9 |
| 233 |
8 |
8 |
8 |
| 377 |
17 |
8 |
8 |
| 610 |
7 |
7 |
7 |
| 987 |
24 |
6 |
6 |
| 1,597 |
22 |
4 |
4 |
| 2,584 |
19 |
10 |
1 |
| 4,181 |
14 |
5 |
5 |
| 6,765 |
24 |
6 |
6 |
| 10,946 |
20 |
2 |
2 |
| 17,711 |
17 |
8 |
8 |
| 28,657 |
28 |
10 |
1 |
| 46,368 |
27 |
9 |
9 |
| 75,025 |
19 |
10 |
1 |
| 121,393 |
19 |
10 |
1 |
| 196,418 |
29 |
11 |
2 |
| 317,811 |
21 |
3 |
3 |
| 514,229 |
23 |
5 |
5 |
| 832,040 |
17 |
8 |
8 |
| 1,346,269 |
31 |
4 |
4 |
| 2,178,309 |
30 |
3 |
3 |
| 3,524,578 |
34 |
7 |
7 |
| 5,702,887 |
37 |
10 |
1 |
| 9,227,465 |
35 |
8 |
8 |
| 14,930,352 |
27 |
9 |
9 |
| 24,157,817 |
35 |
8 |
8 |
| 39,088,169 |
44 |
8 |
8 |
| 63,245,986 |
43 |
7 |
7 |
| 102,334,155 |
24 |
6 |
6 |
| 165,580,141 |
31 |
4 |
4 |
| 267,914,296 |
46 |
10 |
1 |
| 433,494,437 |
41 |
5 |
5 |
| 701,408,733 |
33 |
6 |
6 |
| 1,134,903,170 |
29 |
11 |
2 |
| 1,836,311,903 |
35 |
8 |
8 |
| 2,971,215,073 |
37 |
10 |
1 |
| 4,807,526,976 |
54 |
9 |
9 |
| 7,778,742,049 |
55 |
10 |
1 |
| 12,586,269,025 |
46 |
10 |
1 |
| 20,365,011,074 |
29 |
11 |
2 |
| 32,951,280,099 |
48 |
12 |
3 |
| 53,316,291,173 |
41 |
5 |
5 |
| 86,267,571,272 |
53 |
8 |
8 |
| 139,583,862,445 |
58 |
13 |
4 |
| 225,851,433,717 |
48 |
12 |
3 |
| 365,435,296,162 |
52 |
7 |
7 |
| 591,286,729,879 |
73 |
10 |
1 |
| 956,722,026,041 |
44 |
8 |
8 |
| 1,548,008,755,920 |
54 |
9 |
9 |
| 2,504,730,781,961 |
53 |
8 |
8 |
| 4,052,739,537,881 |
62 |
8 |
8 |
| 6,557,470,319,842 |
61 |
7 |
7 |
| 10,610,209,857,723 |
51 |
6 |
6 |
| 17,167,680,177,565 |
67 |
13 |
4 |
| 27,777,890,035,288 |
73 |
10 |
1 |
| 44,945,570,212,853 |
59 |
14 |
5 |
| 72,723,460,248,141 |
51 |
6 |
6 |
| 117,669,030,460,994 |
65 |
11 |
2 |
| 190,392,490,709,135 |
62 |
8 |
8 |
| 308,061,521,170,129 |
46 |
10 |
1 |
| 498,454,011,879,264 |
72 |
9 |
9 |
Thanks to Joseph Turbeville for sending “A Glimmer of Light from the Eye of a Giant” and to Helga Hertsig for bringing Jain’s discovery of this pattern to my attention.
Filed Under: Math
https://www.goldennumber.net/fibonacci-24-pattern/ |
|
|
 Primer Primer  Anterior 2 a 3 de 3 Siguiente Anterior 2 a 3 de 3 Siguiente  Último Último  |
|
|
Fibonacci 60 Repeating Pattern
October 30, 2016 by Gary Meisner
The last digit of the numbers in the Fibonacci Sequence form a pattern that repeats after every 60th number:
0, 1, 1, 2, 3, 5, 8, 3, 1, 4, 5, 9, 4, 3, 7, 0, 7, 7, 4, 1, 5, 6, 1, 7, 8, 5, 3, 8, 1, 9, 0, 9, 9, 8, 7, 5, 2, 7, 9, 6, 5, 1, 6, 7, 3, 0, 3, 3, 6, 9, 5, 4, 9, 3, 2, 5, 7, 2, 9, 1
This pattern can be seen in the following list of the first 72 Fibonacci numbers:
| 0 |
0 |
| 1 |
1 |
| 2 |
1 |
| 3 |
2 |
| 4 |
3 |
| 5 |
5 |
| 6 |
8 |
| 7 |
13 |
| 8 |
21 |
| 9 |
34 |
| 10 |
55 |
| 11 |
89 |
| 12 |
144 |
| 13 |
233 |
| 14 |
377 |
| 15 |
610 |
| 16 |
987 |
| 17 |
1,597 |
| 18 |
2,584 |
| 19 |
4,181 |
| 20 |
6,765 |
| 21 |
10,946 |
| 22 |
17,711 |
| 23 |
28,657 |
| 24 |
46,368 |
| 25 |
75,025 |
| 26 |
121,393 |
| 27 |
196,418 |
| 28 |
317,811 |
| 29 |
514,229 |
| 30 |
832,040 |
| 31 |
1,346,269 |
| 32 |
2,178,309 |
| 33 |
3,524,578 |
| 34 |
5,702,887 |
| 35 |
9,227,465 |
| 36 |
14,930,352 |
| 37 |
24,157,817 |
| 38 |
39,088,169 |
| 39 |
63,245,986 |
| 40 |
102,334,155 |
| 41 |
165,580,141 |
| 42 |
267,914,296 |
| 43 |
433,494,437 |
| 44 |
701,408,733 |
| 45 |
1,134,903,170 |
| 46 |
1,836,311,903 |
| 47 |
2,971,215,073 |
| 48 |
4,807,526,976 |
| 49 |
7,778,742,049 |
| 50 |
12,586,269,025 |
| 51 |
20,365,011,074 |
| 52 |
32,951,280,099 |
| 53 |
53,316,291,173 |
| 54 |
86,267,571,272 |
| 55 |
139,583,862,445 |
| 56 |
225,851,433,717 |
| 57 |
365,435,296,162 |
| 58 |
591,286,729,879 |
| 59 |
956,722,026,041 |
| 60 |
1,548,008,755,920 |
| 61 |
2,504,730,781,961 |
| 62 |
4,052,739,537,881 |
| 63 |
6,557,470,319,842 |
| 64 |
10,610,209,857,723 |
| 65 |
17,167,680,177,565 |
| 66 |
27,777,890,035,288 |
| 67 |
44,945,570,212,853 |
| 68 |
72,723,460,248,141 |
| 69 |
117,669,030,460,994 |
| 70 |
190,392,490,709,135 |
| 71 |
308,061,521,170,129 |
| 72 |
498,454,011,879,264 |
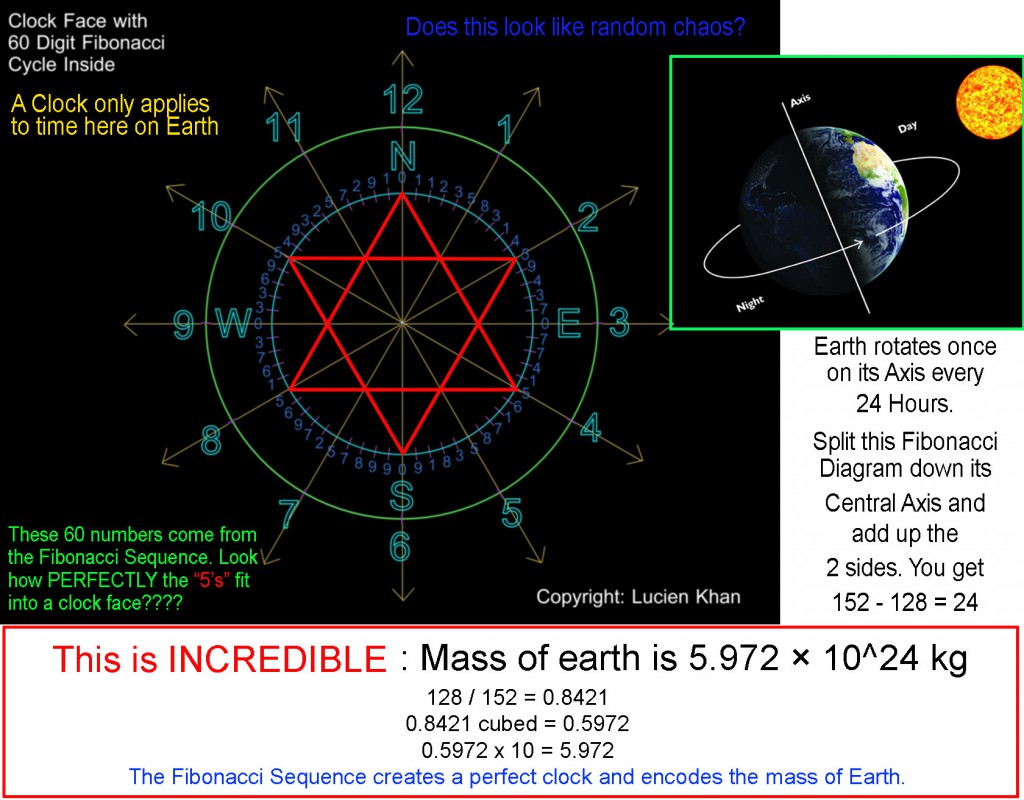
Lucien Khan arranged these 60 digits of the pattern in a circle, as shown in illustration below:
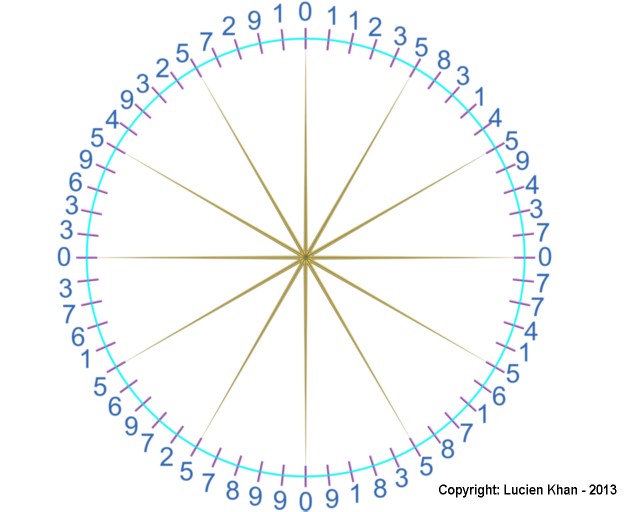
Here he found other interesting results:
- The zeros align with the 4 cardinal points on a compass.
- The fives align with the 8 other points of the 12 points on a clock.
- Except for the zeros, the number directly opposite each number adds to 10.
Lucien postulates that ancient knowledge of these relationships contributed to the development of our modern use of 60 minutes in an hour, and presentation of numbers on the face of the clock.
I found too that any group of four numbers that are 90 degrees from each other (15 away from each other in the circle) sum to 20, except again for the zeros. As an example, use 1, 7, 9 and 3, which appear one to the right of each of the compass points.
Additionally, every group of five numbers that define the points of the 12 pentagons on the circle also create a pattern. Four of the pentagons have even-numbered last digits of 0, 2, 4, 6, and 8. The remaining eight pentagons have odd-numbered last digits of 1, 3, 5, 7 and 9.
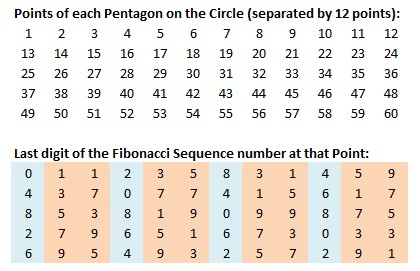
Another interesting pattern yet was observed by Lucien Khan: The 216th number is this sequence is 619220451666590135228675387863297874269396512. The sum of all the digits in that number add up to 216, as well. He notes that it is believed that the secret or hidden name of God contains 216 characters. There are many other fascinating relationships and sacred geometries, which are presented by Lucien Khan in more detail at the links below.
https://www.goldennumber.net/fibonacci-60-repeating-pattern/ |
|
|
|
|
|
|
|


Juan XXIII y Pablo VI, ¿Papas Masones?
"La masonería está por encima de las religiones y de los partidos políticos”. Pero ¿hasta donde sigue existiendo enemistad entre la Iglesia católica y la masonería? En una publicación masónica peruana (2008) Eduardo Seleson afirma lo siguiente: “Hace unos años, el ilustre profesor y licenciado Alfonso Sierra Partida intentó publicar en los periódicos de la ciudad de México D.F. una copia del acta de iniciación en una logia de París donde se deja asentado que el profano Giovanni Montini (Pablo VI) habían sido elevados el mismo día para ser iniciados en los Augustos Misterios de la Francmasonería”. Y prosigue: “Pier Carpi, serio investigador periodístico y en un tiempo fuerte detractor de todo tipo de sociedades iniciáticas o secretas, es, paradójicamente, quien habría de encontrar en el transcurso de sus pesquisas las pruebas documentales de la iniciación masónica en Turquía de Angelo Roncalli (papa Juan XXIII)”. Los detalles de esta historia pueden consultarse en la obra Las profecías de Juan XXIII (Ed. Martínez Roca), de Pier Carpi. Carpi fue miembro de la logia P2 y amigo de su lider, Lucio Gelli, su deus ex machina, sobre el cual escribió un libro exculpatorio.
|
|
|
|
|

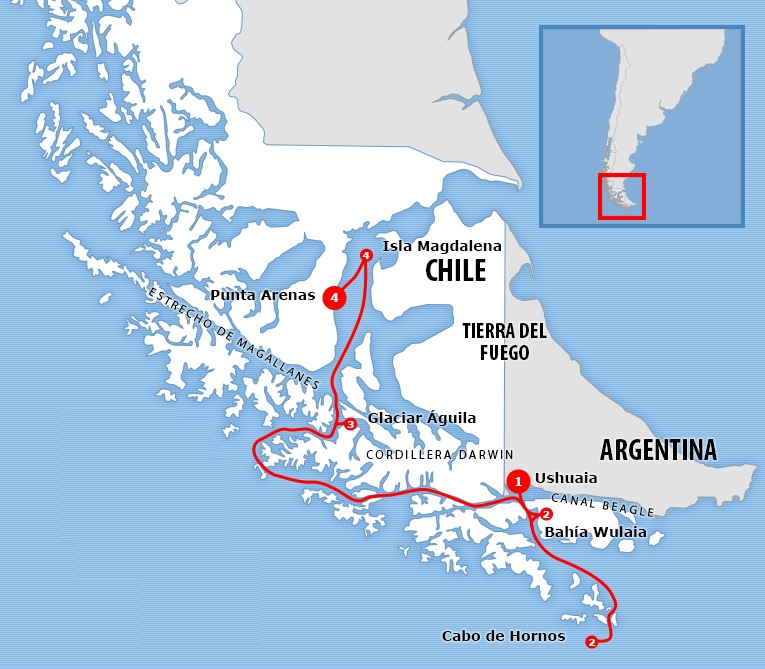   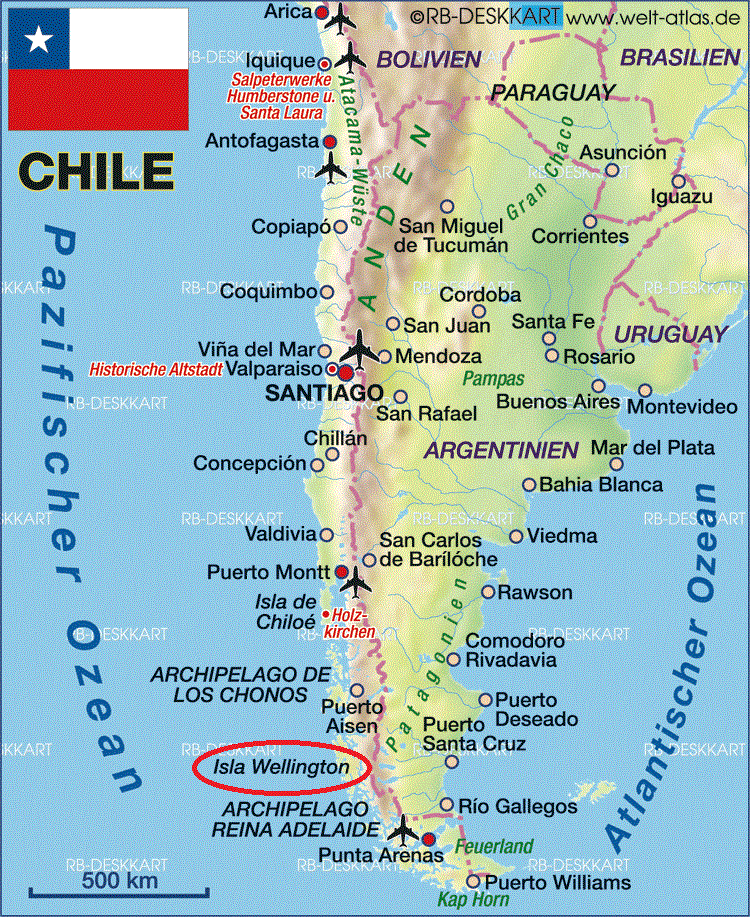 
 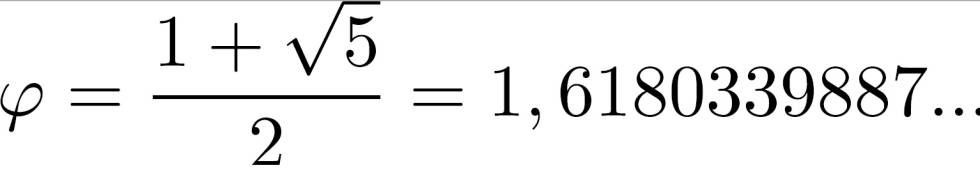
Descubren que la proporción áurea de la bandera de Chile era la más perfecta del mundo: alguien cometió el sacrilegio de cambiarla según los matemáticos
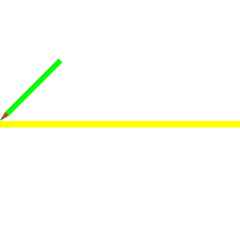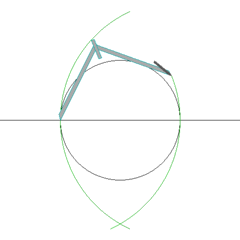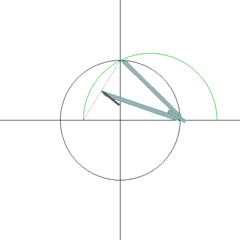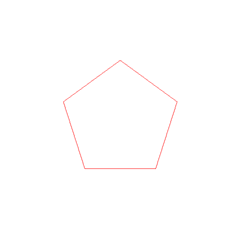
Los antiguos griegos develaron algunos de los misterios matemáticos de la proporción áurea. Por ejemplo, propusieron la primera construcción exacta de un pentágono regular usando regla y compás. Ellos también fueron sensibles a las propiedades estéticas y lo implementaron en el diseño de decoraciones y construcciones.
De hecho, la letra griega ϕ (phi) fue acuñada en honor al célebre escultor Fidias, quien siguió patrones áureos en la elaboración de las esculturas que decoraban el Partenón de Atenas, según publica el diario El País de España.
En cuanto a banderas, la proporción entre el largo y el alto de la de Togo es igual a ϕ (phi) Sin embargo, la que despliega las proporciones áureas en su máximo esplendor es una bandera casi olvidada, aquella con la que Chile firmó su independencia hace 200 años.
Al igual que varios países de Latinoamérica, el proceso independentista chileno se inspiró en las ideas libertarias e iluministas de Francia y EE.UU. recogidas, entre otras, por las logias masónicas. Los colores elegidos para la bandera del país naciente, blanco, azul y rojo, son una muestra evidente de esto. Más aún, su diseño geométrico perfecto revela una conexión muy profunda. En él, ϕ aparece en varias proporciones: entre los largos de los campos blanco y azul entre el alto de la parte azul y el diámetro de la circunferencia en la cual se inscribe la estrella, y entre las partes del lado azul delimitadas por las proyecciones de los ejes de la estrella.
La última propiedad se logra gracias a que el sector azul corresponde a un rectángulo especial, en el cual se despliega una configuración angular de 36, 72, y 108 grados, muy similar a la que aparece en un pentágono regular.
Varios misterios rodean a este diseño. ¿Quién lo hizo? ¿Por qué no se guardó ningún registro? ¿Quiénes poseían este conocimiento y se encargaron de enseñarlo hasta fines del siglo XIX? ¿Por qué nadie dio testimonio de la presencia de la razón áurea por casi 200 años, hasta que el filósofo y experto en estética chileno Gastón Soublette dio con ella?
Increíblemente, todas estas preguntas siguen sin respuesta. Sobre el diseño, se supone que este habría sido en parte ideado por el libertador Bernardo O’Higgins, correspondiendo la implementación técnica a un ingeniero militar. Aquí la opinión de los historiadores se divide: algunos postulan a Antonio Arcos y otros a Gregorio de Andía y Varela. Una curiosidad: ambos eran de origen español, pero intervinieron en favor de Chile durante la guerra.
La Bandera de la Independencia es conservada en el Museo Histórico Nacional de Santiago. En 1912, las proporciones de la bandera chilena fueron modificadas (y simplificadas), perdiéndose así gran parte del simbolismo de este emblema. Fue un verdadero sacrilegio geométrico.
https://cambio21.cl/tendencias/descubren-que-la-proporcin-urea-de-la-bandera-de-chile-era-la-ms-perfecta-del-mundo-alguien-cometi-el-sacrilegio-de-cambiarla-segn-los-matemticos-5c254030aa2d74685c268a78
|
|
|
 Primer Primer
 Anterior
65 a 79 de 94
Siguiente Anterior
65 a 79 de 94
Siguiente Último
Último
|