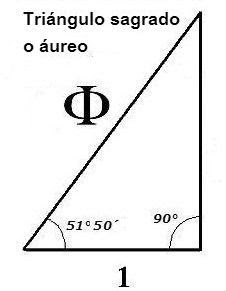
¿Qué es phi?
Phi y la serie de Fibonacci
Funciones trigonométricas
Razones matemáticas
Pentágono
Espirales Áureas
Inicio :: Ver temas relacionados: Decalogo Geometria Sagrada :: Número de Oro :: Merkaba
¿Qué es phi?
Phi (1.618033988749895... ), pronunciado como fi, es un numero irracional como Pi ( 3.14159265358979... ), pero con muchas características matemáticas inusuales. Phi es la base de la Proporción Dorada. La razón o proporción determinada por Phi (1.618...) era conocida por los Griegos como la “Sección Dorada” y por los artistas del renacimiento como la “Proporción Divina”. También se le conoce como la razón Dorada o la Proporción Áurea.
Phi, como Pi, es una razón definida por una construcción geométrica.
Pi es la relación de la circunferencia de un círculo respecto a su diámetro. Phi es la proporción de los segmentos de una línea que resultan cuando una línea es dividida de una forma única y especial.
La línea es dividida para que la proporción de la longitud de la línea entera (A) respecto a la longitud del segmento de la línea mayor (B) sea igual que la proporción de la longitud del segmento de la línea mayor (B) a la longitud del segmento de la línea menor (C)

Esto es que A es 1.618... veces B, y B es 1.618… veces C. Recíprocamente, C es 0.618... de B y B es 0.618... de A. Phi con mayúscula "Phi" es 1.6180339887..., mientras que phi con minúscula es 0.6180339887, el reciproco de Phi o Phi menos 1.
Lo que hace a phi incluso mas inusual es que puede derivarse de muchas formas y ser encontrado en proporcionalmente en el universo. Phi F puede ser derivado por: la serie numérica descubierta por Leonardo Fibonacci, matemáticas y geometría.
Phi y la serie de Fibonacci
Leonardo Fibonacci, por herencia del mundo árabe, descubrió la serie que nos lleva a phi. En el siglo XII, Leonardo Fibonacci descubrió una serie numérica simple que es la base de la increíble relación que encontramos detrás de phi. Empezando con 0 y 1, cada número de la serie es simplemente la suma de los dos anteriores. Así: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .
La razón (proporción) de cada par sucesivo de números en la serie se aproxima a phi (1.618. . .). Así si dividimos 5 entre 3 es 1.666..., y 8 entre 5 es 1.60. En la medida en la que vamos mas lejos del 0 (punto de inicio de la secuencia) nos acercamos al valor de phi.
La tabla de abajo nos muestra como las proporciones de números sucesivos en la serie Fibonacci se aproxima a Phi.
Puedes computar cualquier número de la serie Fibonacci fácilmente. Usa phi para saber cualquier numero (n) de la serie Fibonacci (f)
fn = Fn / 5½
Phi puede derivarse matemáticamente resolviendo la ecuación:
n2 - n1 - n0 = 0 que es lo mismo que n2 - n - 1 = 0
Esta ecuación la rescribimos y nos queda así:
n2 = n + 1 y 1 / n = n - 1
La solución a la ecuación es la raíz cuadrada de 5 más 1 dividido entre 2
( 5½ + 1 ) / 2 = 1.6180339... = F
Esto resulta en dos propiedades únicas de phi:
Si elevas al cuadrado a phi, obtienes un numero exactamente 1 mayor que phi: 2.6180...
F2 = F + 1
Si divides a phi entre 1, obtienes un numero exactamente a 1 menos phi: 0.6180...:
1 / F = F - 1
Phi, curiosamente, puede ser expresado en cinco: 5 ^ .5 * .5 + .5 = F
Puedes usar phi para computar un número n en la serie Fibonacci (fn): fn = Fn / 5½
Como por ejemplo, el número 40 de la serie Fibonacci es 102, 334, 155, que puede expresarse
f40 = F40 / 5½ = 102,334,155
Este método en realidad nos provee un estimado que siempre esta cerca del numero correcto Fibonacci.
http://www.iuca.net/gs/que%20es%20phi.htm