"The modern extension of this axis (completed in 1972) to the ancient Egyptian Temple of Debod exposes who the Vatican really worships.." -Scott Onstott
Repeating Ones
To understand the repeating ones phenomenon let's start with the two ones in the number 11.
Paired Obelisks / Pillars / Minarets / Towers
All of the following structures and symbols read as monumental 11s.
Temple of Luxor

Solomon's Temple
Boaz is known as the pillar of strength or severity and represents the Sun. Jachin is known as the pillar of beauty or mildness and represents the Moon. Boaz and Jachin are built into the architecture of all masonic lodges.

Kaaba in Mecca

Chartres Cathedral

The Pillars of Hercules
One pillar is on Africa and the other on Europe across the straight of Gibraltar. Here the pillars are on the foreword to Sir Francis Bacon's Novum Organum (1620). Francis Bacon is said to be the grandfather of Freemasonry.

Priestess Tarot Card
Boaz and Jachin are B and J below. Note the hypostyle capitals from the Temple of Karnac in Egypt. The pomegranates (which Hades tricked Persephone into eating) are arranged in the Tree of Life pattern. The high priestess is the third column. Note the Torah in her arms, the throne she sits on, and the moon at her feet and Da’at on her head.

Illuminati High Priestess Sex Kitten, Lady Gaga Enthroned Between Pillars in Masonic Lodge:
Her hands emphasize Boaz over Jachin, severity over mildness, strength over beauty.

Above image from this article that exposes what Lady Gaga is all about.
Former World Trade Center in NYC:
If you count the roof level, the north and south towers each had 111 floors.
North Tower 1 WTC: 1,368 ft (Boaz)
South Tower 2 WTC: 1,362 ft (Jachin)

Image courtesy Jeffmock under the Creative Commons Attribution-Share Alike 3.0 Unported license.
I recommend watching the entire video series entitled “Do You Believe in Magick” for a mind opening exposé on the symbolism surrounding the Twin Towers, 9/11, and much more.
|
New York City and George W Bush each have 11 letters. NY was the 11th state admitted to the union.
What 11 is Ultimately About
My personal opinion about what 11 is all about is integrating our bicameral minds into a state of balanced consciousness. Schooling emphasizes the left brain at the expense of the right. Advancement in society is almost entirely a left brained affair. The feminine right side of our consciousness is being systematically suppressed.
Psychic health comes when both hemispheres of the brain are more evenly matched. Artists shouldn't be starving and psychopaths shouldn't be running the world. Extremes flourish because of the imbalance in human consciousness that desperately needs to be healed.
Image courtesy Wyglif under the Creative Commons Attribution-Share Alike 3.0 Inported license.
The Future: Hermitage Plaza in Paris
Hermitage Plaza is a project of two towers to be built on the newly named Place Napoleon Bonaparte (who was responsible for amazing secret architecture, see my Paris episodes) commencing construction this year. The tallest of the two towers will be one meter shorter than the Eiffel Tower at 323 m, making this project the tallest in the European Union when it will be completed in 2016. The twin Hermitage Plaza towers will eventually eclipse the Shard (which is currently under construction in London) as the tallest building in the EU.

Image fair use from project’s official site
The name "Hermitage Plaza" reminds me of The Hermit tarot card. The Hermit is of course another light bringer.

Hermitage Plaza was designed by Foster + Partners and revealed by Sir Norman Foster himself on 3/11/09, exactly two years before the Fukushima nuclear disaster.
Here is some intriguing Atonist copy from the official site:
"The crystalline forms attract the sun beams, animating the buildings throughout the day with changing patterns of light -- coming alive at every opportunity and creating an atmosphere worthy of THE CITY OF LIGHT. [capitalization sic]"
One tower is slightly taller than the other, just like at the former World Trade Center in Manhattan. The tallest of the two will have 93 floors which is a very interesting number...
Thelema
The number 93 is of great significance in Thelema, a religious philosophy founded by English author and occultist Aleister Crowley with the writing of The Book of the Law. The word thelema equates to 93 using Greek isopsephy, which is like gematria in Hebrew.
Thelema = Θελημα
Θ (Theta) = 9 +
ε (Epsilon) = 5 +
λ (Lambda) = 30 +
η (Eta) = 8 +
μ (Mu) = 40 +
α (Alpha) 1
= 93
|
The philosophy of Thelema is expressed in these 11 words:
|
"Do what thou wilt shall be the whole of the Law."
|
Here's what wikipedia article on 93 states:
"It is common for Thelemites to greet each other with “93″ in person as well as in the opening and closing of written correspondence. This custom derives from Aleister Crowley's guideline that Thelemites should greet each other with the Law of Thelema by saying “Do what thou wilt shall be the whole of the law.” Since saying the entire Law can be cumbersome, using 93 has become a kind of shorthand."
Aleister Crowley wrote this on the matter:
"I am often asked why I begin my letters this way. No matter whether I am writing to my lady or to my butcher, always I begin with these eleven words. Why, how else should I begin? What other greeting could be so glad? Look, brother, we are free! Rejoice with me, sister, there is no law beyond Do what thou wilt!"
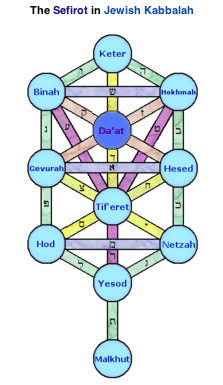
Kabbalistic Tree of Life
There are 10 sephiroth in the Tree of Life from the Jewish Kabbalah plus a hidden one called Da’at (or Daath) that unites all 11.
Humans who become self-giving like the Light become able to see it, and for them the benefits of Daat's Light seem "revealed". However, humans who remain selfish cannot see it, and for them its benefits seem "hidden".
|
Apollo 11
Apollo 11 was the first mission that supposedly reached the moon.

Executive Order 11110
In his book Crossfire: The Plot That Killed Kennedy, Jim Mars argues that what got JFK killed was signing of Executive Order 11110 which was an attempt to wrest control of the monetary policy of the US away from the Federal Reserve Bank.
Executive Order 11110 was signed on 4 June 63 and JFK was assassinated on 22 Nov 63.
JFK was killed 11+11 days into the 11th month of 1963.
Triangle / Pyramid Numbers
Any product of repeating ones makes a triangle or an Egyptian pyramid if you will: 11×11=121, 111×111=12321, 1111×1111=1234321, etc.

Arago Markers in Paris
There are 121 (11×11) documented bronze medallions in a line across Paris marking the Paris prime meridian which was used in France for 200 years before Greenwich UK became the world's prime meridian. The metric system was defined using the Paris prime meridian. Arago was a French astronomer.

Football / Soccer
Football or soccer as it is known in the United States has amazing numerical symbolism. 11 players on one team compete against 11 players on the other team. The ball is the spherical marriage of hexagon and pentagon having 32 panels. The world's most popular sport therefore appears to be a Masonic invention.

The Mayan Calendar
The end date of the Mayan calendar is 21 Dec 2012 at 11:11 AM GMT.
Image of Hunab Ku, the galactic center worshipped by the Mayans.
The end of the Mayan calendar corresponds to when Earth passes the galactic center.
The Big Empty
This mysterious movie from 2003 encodes repeating ones in occult symbols. Here are the protagonist John Person's bowling shoes. He stayed in motel room 111. The movie builds to a rendezvous with a UFO. Personally I think the movie sucks except for the cleverly encoded symbolism. Here is an image from the end of the movie:

Fair use screen capture ofThe Big Empty
Final dialogue in The Big Empty:
John Person: "You look different tonight."
Grace: "It's the tenth frame. You get one more chance. Make it count. Then you start a new game."
|
In ten-pin bowling, there are only 10 frames. Grace says there is one more chance making an eleventh frame, and John Person proceeds to bowl one last time. The bowling ball rolls down the alley and then it cuts to a bowling ball rolling across the desert. Very intriguing. By the way ten pin bowling has the pins arranged in the Pythagorean tetractys, the most sacred diagram in the Pythagoreans secret worship of number. Many sports encode secrets in plain sight. I’ll cover Masonic Baseball in a future post.

Image courtesy Stefan Grazer under the Creative Commons Attribution-Share Alike 3.0 Unported license
Statue of Liberty
The height of the Statue of Liberty is 111′-1″ from bottom of foot to top of head. The 7 rays on the crown and the 11 points of the base star echo the proportions of the Great Pyramid’s 7:11 height to base proportion. The superb book Talisman by Graham Hancock and Robert Bauval convincingly shows this goddess is actually the Egyptian Isis.

Image courtesy Elcobbola under the Creative Commons Attribution-Share Alike 3.0 Unported license.
The Great Pyramid
According to Richard Heath's metrology in Sacred Number (well worth reading by the way) the Great Pyramid (GP) measures 480 English feet to the top of the "unfinished pyramid" which happens to be precisely 1/11th of a mile.
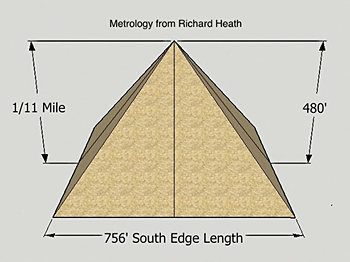
The pyramidion measured 1-1/11 feet in height. Herodotus tells us it was made of electrum and brilliantly reflected light (electrum is an alloy of gold and silver). The valuable pyramidion is long gone of course.
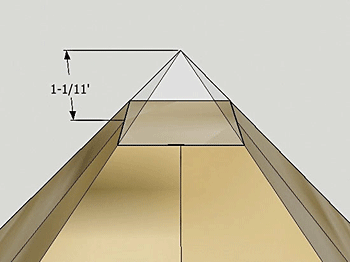
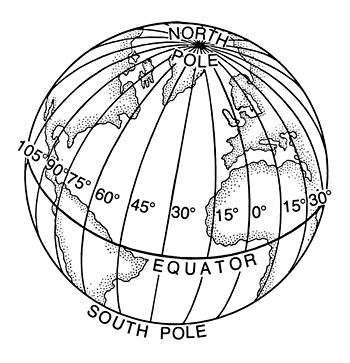
Earth Longitude
One degree of longitude measures 111,111 meters at the equator. How can this be?
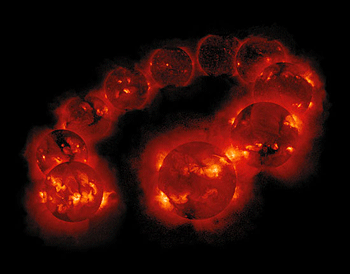
The Solar Cycle
The amount of solar radiation received on Earth rises and falls in an 11 year cycle. This is called the solar cycle.
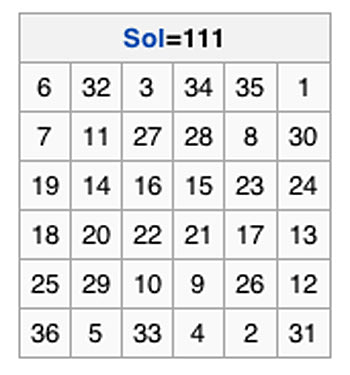
Magic Square of the Sun
In the traditional magic square of the Sun every row, column and diagonal adds up to 111.
Templars
The nine founding templars first banded together in 1111 AD.

Templar flag courtesy of Lexicon under Creative Commons Attribution-Share Alike 3.0 Unported license.
Chartres Labyrinth and Ptolemaic Cosmology Both have 11 concentric rings.
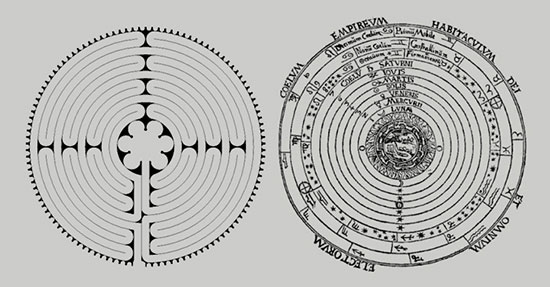
Important Addresses
1111 California Street is Masonic Center at the top of Nob Hill in San Francisco, directly across from Grace Cathedral which features a replica of the Chartres labyrinth depicted above.

Fair use image straight from the source
There is a frieze on the building exterior representing a gigantic tug of war between good and evil forces where they are pulling on the Sun. The interior strangely contains gravel and soil from each of the 58 counties in California, suggesting some kind of sympathetic magic at work.
111 Cannon Street is the address of the London Stone at the base of the street pyramid in the City of London. This is the stone the Romans laid as the omphalos stone, the point from which all distances were measured in Britainnia.
The London Stone is recognized as the symbolic authority and heart of the City of London. It was the place where deals were forged and oaths were sworn. It was also the point from which official proclamations were made.

1111 Constitution Avenue NW in Washington DC is the headquarters of the Internal Revenue Service.

Image courtesy Cliff under the Creative Commons Attribution 2.0 Generic license.
Remembrance Day
The major hostilities of World War I were formally ended on the 11th hour of the 11th day of the 11th month of 1918 with the German signing of the armistice. As a result Remembrance Day is observed on 11/11 at 11 AM in commonwealth countries.
The Shrine of Remembrance was built in Melbourne Australia in 1934 to help people remember Remembrance Day. One third of the population of the time came out on opening day. The building features an Egyptian style truncated pyramid on top.

The core of the building houses the Stone of Remembrance. This is a marble stone sunk below the pavement, so that visitors must bow their heads to read the inscription on it:
|
"GREATER LOVE HATH NO MAN"
|
The Stone is aligned with an aperture in the roof so that a ray of sunlight falls on the word LOVE on the Stone of Remembrance at exactly at 11 AM on the 11th day of the 11th month. The beam of light hitting the word LOVE is an appropriate touch for anyone who loves the light.

Cenotaphs
Cenotaph means empty tomb. A cenotaph marks the remains of a person or group of people whose remains remain elsewhere. This cenotaph in London says "The Glorious Dead" to honor those soldiers who died in WWI. Red wreaths or red poppies are left at these geomantic markers representing the blood split in war. Very morbid to glorify death and blood when you think about it. How about celebrating these young men’s lives rather than their spilled blood? Here is the cenotaph in London but they are all over the world in commonwealth countries.

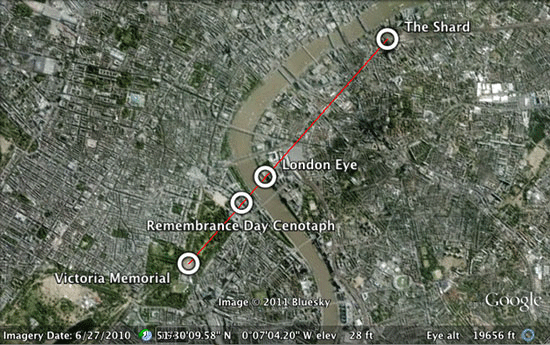
London Alignment
Here's an intriguing alignment I discovered in London. A straight line connects the Victoria memorial in front of Buckingham Palace with the aforementioned Remembrance Day cenotaph, goes through the highly symbolic 444′ high, 32 car London Eye and continues to The Shard whose address is 32 London Bridge. 32 is of course an important Masonic number in the Scottish rite.
111,000 Square Meters
The Shard at 32 London Bridge will be the tallest building in the EU for a few years before it is eclipsed by Hermitage Plaza in Paris. Architect Renzo Piano’s structure is currently under construction and has 72 habitable floors comprising a floor area of 111,000 m2

In the Kabbalah the number 72 is called the Shemhamphorasch referring to the number of names of God.
The IM Pei (of Louvre Pyramid fame) designed Fountain Place and the SOM designed Trammel Crow Center (with pyramid on roof) both on Ross Avenue (rose or rosicrucian symbol) in Dallas Texas have exactly the same symbolic floor area of 111,000 m2
The Bank of America
The Bank of America logo encodes both 11:11 and 33. Two pairs of red elevens encodes 11:11.

Image courtesy of Brian Katt under the Creative Commons Attribution-Share Alike 3.0 Unported license.
Three pairs of both red and blue elevens encodes 33. See this post for all things 33.
Rik Clay's 11:11 Research
This Red Ice Creations interview will blow your mind about the symbolism swirling around 11:11. Hour one and hour two.
http://www.viewzone.com/onstott66.html

