|
|
General: La Parábola del Aguador
إختار ملف آخر للرسائل |
|
جواب |
رسائل 1 من 38 في الفقرة |
|
| من: Alcoseri (الرسالة الأصلية) |
مبعوث: 06/11/2016 16:36 |
La Parábola del Aguador
Un masón preguntó a un Sublimado
Maestro Masón si le podía enseñar la
Palabra Perdida, esa mítica Palabra tan Poderosa que al pronunciarla producía portentosos milagros,
alterar el curso de Naciones y cambiar así la historia, esa Mágica Palabra que los malos albañiles
del Templo dedicado a Dios en Jerusalén
pretendieron arrancar de los labios del Maestre de Obras del Templo Hiram Abiff, y que al negarse a dárselas los obreros le
asesinaron. El sublimado masón dijo así al Masón: nadie puede saber la
verdadera palabra de un Maestro Masón,
no hasta que es merecedor de ella. Hoy durante la exaltación la palabra sagrada
no sería más que la sustituta de esta poderosa palabra.
El Sublimado Maestro Masón entonces
dijo:
De acuerdo con la tradición masónica,
primero tengo que hacerte la prueba que demostrará tu capacidad. Irás al mercado de la ciudad y permanecerás allí
hasta caída la noche, regresarás entonces a la media noche en punto para
describir lo que hayas presenciado y más te haya impresionado.
El Masón que pretendía conocer la
Palabra del Poder Masónico, ilusionado, hizo lo que el Sublimado Masón que está
más allá de los grados masónicos tradicionales le dijo que hiciera. A la caída de
la noche regresó e informó al Sabio sublimado masón que está más allá del grado
33°.
Siguiendo sus instrucciones – dijo el
Masón, y agregó: me puse a vigilar en el Mercado de la Ciudad. El incidente que
más me impresionó de todo el tiempo que ahí estuve se refiere a un vendedor de
frescas y dulces aguas de sabores. El anciano vendedor fue asediado por un
inspector de sanidad, y pretendía el inspector extorsionarlo quitándole gran
parte del dinero que había ganado durante todo su día de trabajo.
El Inspector de Sanidad insistió en
que le diera más de la mitad de sus ganancias, el vendedor insistía en que el
agua que vendía era purificada, eso no le importó al inspector de Sanidad
pública. El viejo vendedor de Aguas, se notaba contrariado y empobrecido, pidió
le diera la oportunidad pues tenía que comprar medicamentos para su esposa
enferma, eso no le importó al Inspector. Dándose cuenta de que el viejo
vendedor de aguas frescas estaba desamparado, el inspector le arrebató la bosa que contenida las monedad ganadas durante
el día de trabajo, sacó más de la mitad
de las monedas, le dio un golpe al vendedor de aguas y se largó.
El Sublimado Maestro Masón preguntó:
¿Cuáles fueron tus sentimientos
cuando viste eso?
El masón contestó:
Deseé más que nunca conocer esa
palabra poderosa de los masones sublimados, esa palabra que puede cambiar el
rumbo de las Naciones, esa palabra que
puede derrocar tiranos, esa palabra que puede resucitar a los muertos, y hacer se haga justicia. Si la
hubiese conocido, la situación entre el vendedor de aguas frescas y el
inspector de sanidad habría sido diferente, el desafortunado e inocente aguador
hubiera sido ayudado por mí, y castigado por mí el abusivo inspector de
sanidad.
El Muy Sublimado Maestro Masón,
exclamó: ¡Oh, mi hermano masón, nacido de una madre viuda! Yo mismo recibí la Palabra Perdida de mi
propio Maestro Ascendido, después que me hubo puesto a prueba, y visto mi resolución
y averiguado si yo era digno de poder
utilizar bien tan poderosa palabra,
quiso saber si yo era un simple impulsivo emocional, un pasional
obsesivo o un buen sirviente del ser humano, y después de haberme sometido a
diversas experiencias que me permitieron a mí mismo ver mis propios
pensamientos y mi conducta.
El Poder de la Palabra Masónica, recuerda
bien, pudo hacer que el Maestre Hiram fulminara a los malos albañiles que le
pretendieron robar la palabra mágica. La Palabra Perdida es el nombre del Mismo Jehová y es siempre para el
servicio de toda la humanidad. Mi
Maestro no fue otro que el vendedor de Aguas Frescas del mercado, si el Aguador
(Acuario). Y el Inspector de sanidad no
es otro que el Mismo Sol, el que me puso a mí a prueba antes de que yo
recibiera la Palabra que da Vida en abundancia. ---
Alcoseri.
|
|
|
|
جواب |
رسائل 9 من 38 في الفقرة |
|
|
|
|
جواب |
رسائل 10 من 38 في الفقرة |
|
|
|
|
جواب |
رسائل 11 من 38 في الفقرة |
|
SARA=SERPIENTE=$
|
|
Génesis 8:22 Mientras la tierra permanezca, no cesarán la sementera y la siega, el frío y el calor, el verano y el invierno, y el día y la noche. (EL MISMO DISEÑO DEL VATICANO-OCHO PUNTAS-PLAZA DE SAN PEDRO)
DINERO=MUJER=$=SARA
EL PSEUDOCRISTIANISMO LE TIENE PANICO A LA MUJER.
|
|
EN VENECIA ESTA EL SECRETO
|
Obviamente que Dios es Dios de vivos..
Puesto que en la fe nadie muere..
Y los patriarcas Abraham, Isaac, Jacob ..
Caminaron por fe..
Dios le cambio el nombre de abram a abraham..
Porque es el primer viviente según el pacto de la circuncisión..
El primer hombre de fe, el padre de naciones..
Y ese pacto de Dios con Abraham sigue vigente hasta hoy..
Porque en la fe de Abraham son salvas todas las naciones..
Y para dejar tranquilo a Barilochense le digo :
Dios también le cambió el nombre a la mujer de Abraham..
De Saraí ( princesa ) pasó a llamarse Sara que significa madre de naciones..
16. Y la bendeciré, y también te daré de ella hijo; sí, la bendeciré, y vendrá a ser madre de naciones; reyes de pueblos vendrán de ella.
Para que no diga que Dios no ama a sus hijas..
Saludos
El Ungido
|
|
|
|
|
جواب |
رسائل 12 من 38 في الفقرة |
|
ISLA SAN GIORGIO (VENECIA)=GEORGE LEMAITRE
GEMATRIA EN INGLES DE SEED=33
GEMATRIA EN INGLES DE GATE=33
SARA (CE-SAREA DE FILIPO)=PARALELO 33
 the Apple
| milky way in Simple Gematria Equals: 119 |
( |
m 13 |
i9 |
l 12 |
k 11 |
y 25 |
0 |
w 23 |
a1 |
y 25 |
) |
| queen mary in Simple Gematria Equals: 119 |
( |
q 17 |
u 21 |
e5 |
e5 |
n 14 |
0 |
m 13 |
a1 |
r 18 |
y 25 |
|
| hebrew calendar in Simple Gematria Equals: 119 |
( |
h8 |
e5 |
b2 |
r 18 |
e5 |
w 23 |
0 |
c3 |
a1 |
l 12 |
e5 |
n 14 |
d4 |
a1 |
r 18 |
| mary magdalene in Simple Gematria Equals: 119 |
( |
m 13 |
a1 |
r 18 |
y 25 |
0 |
m 13 |
a1 |
g7 |
d4 |
a1 |
l 12 |
e5 |
n 14 |
e5 |
|

|
|
|
|
جواب |
رسائل 13 من 38 في الفقرة |
|
|
|
Hércules (constelación)
De Wikipedia, la enciclopedia libre
Recibe su nombre del héroe mitológico, Hércules y es la quinta en tamaño de las 88 constelaciones modernas. También era una de las 48 constelaciones de Ptolomeo.
[editar] Características destacables
No tiene estrellas de primera magnitud, siendo la más brillante β Herculis con magnitud 2,78. μ Herculis se encuentra a 27,4 años luz de la Tierra. El Ápex solar (punto del cielo que indica la dirección hacia la que se mueve el Sol en su órbitaalrededor del centro de la galaxia) se encuentra en Hércules, cerca de ξ Herculis.
[editar] Estrellas principales
- α Herculis (Ras Algethi o Rasalgethi), de magnitud 3,31, es un sistema estelar triple, cuya estrella principal es una gigante roja variable.
- β Herculis (Kornephoros), la más brillante de la constelación con magnitud 2,78, una estrella gigante amarilla.
- γ Herculis, gigante blanca de magnitud 3,74. Es una binaria espectroscópica con un período orbital de 11,9 días.
- δ Herculis (Sarin), estrella blanca de magnitud 3,12; es una estrella binaria cuyas componentes han sido resueltas por interferometría.
- ε Herculis, binaria espectroscópica de magnitud 3,91.
- ζ Herculis, la segunda más brillante de la constelación con magnitud 2,89, estrella doble formada por dos estrellas amarillas de desigual brillo.
- η Herculis, gigante amarilla de magnitud 3,49.
- θ Herculis, gigante luminosa naranja de magnitud 3,85.
- ι Herculis, subgigante azul de magnitud 3,79; tres estrellas más completan este sistema estelar cuádruple.
- κ Herculis A y κ Herculis B, dos gigantes que forman una doble óptica.
- λ Herculis (Maasym), gigante naranja de magnitud 4,40.
- μ Herculis, sistema estelar cercano que dista del Sistema Solar 27,4 años luz.
- π Herculis, gigante naranja de magnitud 3,16.
- ρ Herculis, estrella doble cuyas componentes, separadas 4 segundos de arco, brillan con magnitud 4,56 y 5,42.
- τ Herculis, estrella B pulsante lenta (SPB) con una tenue compañera a 7,6 segundos de arco.
- χ Herculis, enana amarilla de baja metalicidad que se encuentra a 52 años luz de distancia.
- ω Herculis (Kajam), de magnitud 4,57.
- 8 Herculis, estrella blanca de magnitud 6,13 que forma una doble óptica con Kappa Herculis —separación 0,2º—.
- 14 Herculis, enana naranja a 59,2 años luz con una enana marrón o planeta gigante alrededor. En 2006 se descubrió un posible segundo compañero, aún sin confirmar.
- 30 Herculis (g Herculis), gigante roja y variable semirregular cuyo brillo oscila entre magnitud 4,3 y 6,3 en un ciclo de 89,2 días.
- 68 Herculis (u Herculis), binaria eclipsante en donde existe transferencia de masa desde la secundaria hacia la primaria.
- 72 Herculis (w Herculis), enana amarilla similar al Sol a 47 años luz de distancia.
- 89 Herculis, supergigante amarilla en las etapas finales de su evolución estelar.
- 95 Herculis, estrella binaria compuesta por una gigante blanca y una gigante amarilla separadas 6,3 segundos de arco.
- 99 Herculis, binaria de baja metalicidad cuya primaria es una enana amarilla de magnitud 5,20.
- 101 Herculis, gigante blanca de magnitud 5,11.
- 109 Herculis, gigante naranja de magnitud 3,84, la duodécima estrella más brillante de la constelación.
- 111 Herculis, estrella blanca de magnitud 4,35.
- X Herculis, variable pulsante semirregular cuyo brillo varía entre magnitud 6 y 7 en un período de 95 días.
- SZ Herculis y FN Herculis, binarias eclipsantes de magnitud 9,94 y 11,08 respectivamente.
- UX Herculis, binaria eclipsante de magnitud 9,05; durante el eclipse principal su brillo disminuye 1,16 magnitudes.
- OP Herculis, gigante luminosa roja variable entre magnitud 5,85 y 6,73.
- HD 147506, subgigante amarilla en donde se ha detectado un planeta masivo (HAT-P-2b) en una órbita excéntricacercana a la estrella.
- HD 149026, estrella subgigante con un planeta cuya masa es similar a la de Saturno.
- HD 154345, enana amarilla a 58,91 años luz con un planeta extrasolar.
- Gliese 623, estrella binaria compuesta por dos enanas rojas.
- Gliese 686 y Gliese 649, enanas rojas a 26,5 y 33,7 años luz respectivamente; la segunda de ellas posee un planeta.
- HD 155358, estrella de baja metalicidad con dos planetas que interactúan gravitacionalmente.
- Gliese 638 y HR 6806, enanas naranjas situadas respectivamente a 31,9 y 36,2 años luz de distancia de la Tierra.
- GD 362, enana blanca con un anillo similar a los de Saturno.
- http://es.wikipedia.org/wiki/H%C3%A9rcules_(constelaci%C3%B3n)
  
ISLA SAN GIORGIO (VENECIA)=GEORGE LEMAITRE
GEMATRIA EN INGLES DE SEED=33
GEMATRIA EN INGLES DE GATE=33
SARA (CE-SAREA DE FILIPO)=PARALELO 33
"¡Oh profundidad de las riquezas de la sabiduría (sophia)
y de la ciencia (gnwsiV, gnosis) de Dios!
¡Cuán incomprensibles son sus juicios, e inescrutables sus caminos!"
(Romanos, 11: 33).
25 DE ABRIL=DIA DE SAN MARCOS
22 DE JULIO=DIA DE MARIA LA MAGDALENA
|
|
|
|
|
|
|
جواب |
رسائل 14 من 38 في الفقرة |
|
|
|
|
جواب |
رسائل 15 من 38 في الفقرة |
|
|
|
|
جواب |
رسائل 16 من 38 في الفقرة |
|







 



|

LLAVE DE ORO Y DE PLATA AL IGUAL QUE LA MANZANA
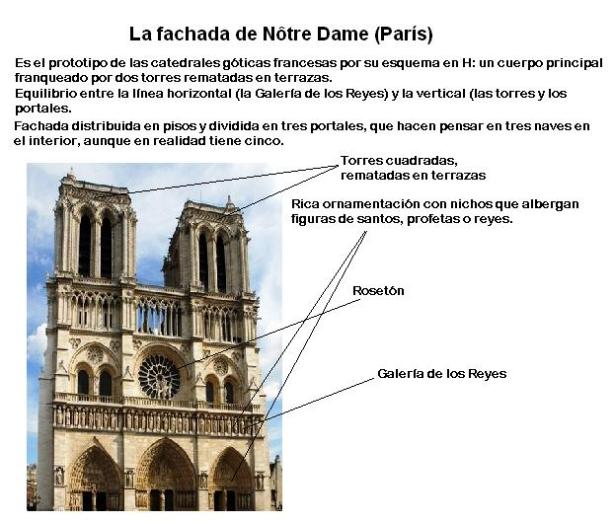
Incendio Notre Dame: Última hora de la catedral de París (15 DE ABRIL)

 Incendio Notre Dame (París), en directo (Bertrand Guay / AFP)
PHI A NOTRE-DAME
A la catredal de Notre Dame hi observem més rectanlges auris: Creat per Mario Pastor 
The DaVinci Code, Notre Dame Cathedral from DaVinci Code
original movie prop
HEXAGONO=OCTAHEDRO =ESTRELLA DE 6 PUNTAS= SATURNO =CUBO/HEXAGONO= ESPACIO/TIEMPO =1 DE REYES 6:20 Y APOCALIPSIS 21:16
EL SEXTO DIA ES EL VIERNES Y EL OCTAVO EL DOMINGO. INCREIBLE
   

August 23, 2018/

The Golden Section (aka Golden Mean, and Golden Ratio) phys.org
We use math in architecture on a daily basis to solve problems. We use it to achieve both functional and aesthetic advantages. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance. As you will see from some of the examples below, the application of mathematical principles can result in beautiful and long-lasting architecture which has passed the test of time.
Using Math in Architecture for Function and Form
We use math in architecture every day at our office. For example, we use math to calculate the area of a building site or office space. Math helps us to determine the volume of gravel or soil that is needed to fill a hole. We rely on math when designing safe building structures and bridges by calculating loads and spans. Math also helps us to determine the best material to use for a structure, such as wood, concrete, or steel.
“Without mathematics there is no art.” – Luca Pacioli, De divina proportione, 1509
Architects also use math when making aesthetic decisions. For instance, we use numbers to achieve attractive proportion and harmony. This may seem counter-intuitive, but architects routinely apply a combination of math, science, and art to create attractive and functional structures. One example of this is when we use math to achieve harmony and proportion by applying a well-known principle called the Golden Section
Math and Proportion – The Golden Section

Perfect proportions of the human body – The Vitruvian Man – by Leonardo da Vinci.
We tend to think of beauty as purely subjective, but that is not necessarily the case. There is a relationship between math and beauty. By applying math to our architectural designs through the use of the Golden Section and other mathematical principles, we can achieve harmony and balance.
The Golden Section is one example of a mathematical principle that is believed to result in pleasing proportions. It was mentioned in the works of the Greek mathematician Euclid, the father of geometry. Since the 4th century, artists and architects have applied the Golden Section to their work.
The Golden Section is a rectangular form that, when cut in half or doubled, results in the same proportion as the original form. The proportions are 1: the square root of 2 (1.414) It is one of many mathematical principles that architects use to bring beautiful proportion to their designs.
Examples of the Golden Section are found extensively in nature, including the human body. The influential author Vitruvius asserted that the best designs are based on the perfect proportions of the human body.
Over the years many well-known artists and architects, such as Leonardo da Vinci and Michelangelo, used the Golden Section to define the dimensions and proportions in their works. For example, you can see the Golden Section demonstrated in DaVinci’s painting Mona Lisa and his drawing Vitruvian Man.
Famous Buildings Influenced by Mathematical Principles
Here are some examples of famous buildings universally recognized for their beauty. We believe their architects used math and the principals of the Golden Section in their design:
Parthenon
The classical Doric columned Parthenon was built on the Acropolis between 447 and 432 BC. It was designed by the architects Iktinos and Kallikrates. The temple had two rooms to shelter a gold and ivory statue of the goddess Athena and her treasure. Visitors to the Parthenon viewed the statue and temple from the outside. The refined exterior is recognized for its proportional harmony which has influenced generations of designers. The pediment and frieze were decorated with sculpted scenes of Athena, the Gods, and heroes.

Parthenon Golden Section
Notre Dame Cathedral in Paris
Built on the Ile de la Cite, Notre Dame was built on the site of two earlier churches. The foundation stone was laid by Pope Alexander III in 1163. The stone building demonstrates various styles of architecture, due to the fact that construction occurred for over 300 years. It is predominantly French Gothic, but also has elements of Renaissance and Naturalism. The cathedral interior is 427 feet x 157 feet in plan. The two Gothic towers on the west façade are 223 feet high. They were intended to be crowned by spires, but the spires were never built. The cathedral is especially loved for its three stained glass rose windows and daring flying buttresses. During the Revolution, the building was extensively damaged and was saved from demolition by the emperor Napoleon.

Notre Dame Cathedral in Paris
Taj Mahal
Built in Agra between 1631 and 1648, the Taj Mahal is a white marble mausoleum designed by Ustad-Ahmad Lahori. This jewel of Indian architecture was built by Emperor Shah Jahan in memory of his favorite wife. Additional buildings and elements were completed in 1653. The square tomb is raised and is dramatically located at the end of a formal garden. On the interior, the tomb chamber is octagonal and is surrounded by hallways and four corner rooms. Building materials are brick and lime veneered with marble and sandstone.

Taj Mahal designed by Ustad-Ahmad Lahori
As you can see from the above examples, the application of mathematical principles can result in some pretty amazing architecture. The architects’ work reflects eye-catching harmony and balance. Although these buildings are all quite old, their designs have pleasing proportions which have truly passed the test of time.
https://bleckarchitects.com/math-in-architecture/
|
|
|
|
|
|
جواب |
رسائل 17 من 38 في الفقرة |
|
|
|
|
جواب |
رسائل 18 من 38 في الفقرة |
|
ES OBVIO EL NEXO DE LA SERPIENTE CON LA MUJER
NOTEN EL NEXO DE DAN, CON LA SERPIENTE (VENECIA) Y EL CABALLO (PLAZA SAN MARCOS)
7. Génesis 49:17 Será Dan SERPIENTE junto al camino, Víbora junto a la senda, Que muerde los talones del caballo, Y hace caer hacia atrás al jinete.
|
|
|
|
جواب |
رسائل 19 من 38 في الفقرة |
|
|
|
|
جواب |
رسائل 20 من 38 في الفقرة |
|
15 mar. 2017 - Subido por Derivando
Qué relación hay entre Albert Einstein, los ríos y el famoso número Pi? Hoy en Derivando te lo vamos a explicar ...
15 mar. 2017 - Subido por Derivando
Qué relación hay entre Albert Einstein, los ríos y el famoso número Pi? Hoy en Derivando te lo vamos a explicar ...
7 dic. 2017 - Subido por Jaume Solsona Villaplana
Einstein, los ríos y el número PI. Jaume Solsona Villaplana. Loading... Unsubscribe from Jaume Solsona ...
15 mar. 2017 - Subido por Derivando
El bloguero de YouTube Eduardo Sáenz explica uno de los descubrimientos de Albert Einstein en relación a la ...
|
|
|
|
جواب |
رسائل 21 من 38 في الفقرة |
|
https://www.kienyke.com/historias/enigmatico-viajar-en-el-tiempo-cuantico
8 ene. 2018 - ... Kurt Gödel un brillante matemático amigo de Einstein, sugirió que para ir al pasado era necesario desdoblar el tiempo a través de un atajo y llegar a cualquier parte antes que la luz. Basados en esta hipótesis, algunos físicos cuánticos de la actualidad descubrieron que los agujeros de gusanos pueden ...
https://matap.dmae.upm.es/cienciaficcion/narraciones/.../agujerosdegusano.htm
Entre éstas se destacan el cilindro de longitud infinita y compuesto de polvo en rotación rápida de Van Stockum, y el universo en rotación propuesto por Kurt Gödel. La matemática de estas soluciones muestra que ambas contienen trayectorias en el espacio-tiempo que permiten viajar hacia el pasado y retornar al ...
www.aecomunicacioncientifica.org/que-dice-la-fisica-sobre-los-viajes-en-el-tiempo/
5 may. 2016 - El viaje se realizaría a través de un wormhole (literalmente, un agujero de gusano), un túnel a través del espacio-tiempo. ... Para terminar, citaré que el famoso matemático Kurt Gödelpropuso en 1949 un modelo cosmológico compatible con la relatividad general, en el que los viajes en el tiempo serían ...
https://books.google.com.ar/books?isbn=6073137427
Kurt Gödel 1 y Kip Thorne2 han demostrado que los agujeros de gusano podrían engendrar unos nudos temporales, unos pasajes del presente hacia el pasado. Así se vuelven verdaderas máquinas para pasear por el tiempo pasado. Si la entrada del agujero de gusano (el agujero negro) es inmóvil en relación con ...
www.lehman.edu/faculty/anchordoqui/tuneles2.htm
Entre estas se destacan el cilindro de longitud infinita y compuesto de polvo en rotación rápida de Van Stockum, y el universo en rotación propuesto por Kurt Gödel. ... Supongamos (figura 3) que existe unagujero de gusano atravesable cuyas bocas, separadas por una distancia mucho mayor que el radio de su garganta, ...
blogs.publico.es/kaostica/2014/11/06/interstellar/
6 nov. 2014 - Antes de adentrarnos en los agujeros de gusano, es preciso entender qué son los agujeros negros y, sobre todo, los menos conocidos agujeros blancos. ... En 1949, Kurt Gödel, buen amigo de Albert Einstein, planteó un modelo cosmológico para un universo en rotación consistente con la Relatividad ...
https://books.google.com.ar/books?isbn=8483230755
Yervant Terzian (ed.), Elizabeth Bilson (ed.) - 1999 - Science
En el lado del agujero de gusano que ocupa Carolee es domingo (aunque solo haya envejecido una hora hasta llegar a este punto). ... gran matemático Kurt Gódel (1949), el universo aparece girando a alta velocidad y dotado de una constante cosmológica, con lo que se convierte en una máquina gigantesca del tiempo.
historiadeltiempo-edgardo.blogspot.com/.../capitulo-10-agujeros-de-gusano-y-viajes.h...
5 may. 2011 - viajes en el tiempo se produjo en 1949 cuando Kurt Gödel descubrió un nuevo. espacio-tiempo permitido por la teoría de la relatividad. Gödel fue un matemático. que se hizo famoso al demostrar que es imposible probar todas las afirmaciones. verdaderas, incluso si nos limitáramos a tratar de probar las ...
 
|
|
|
|
جواب |
رسائل 22 من 38 في الفقرة |
|
|
|
|
جواب |
رسائل 23 من 38 في الفقرة |
|
|
|
 أول أول
 سابق
9 a 23 de 38
لاحق سابق
9 a 23 de 38
لاحق آخر
آخر
|
|
| |
|
|
©2025 - Gabitos - كل الحقوق محفوظة | |
|
|

