Pàgina principal  |  Contacte  

Correu electrònic:

Contrasenya:

Inscriviu-vos ara!

Heu oblidat la vostra contrasenya?
Secreto Masonico
 
Novetats
  Afegeix-te ara
  Plafó de missatges 
  Galeria d’imatges 
 Arxius i documents 
 Enquestes i Tests 
  Llistat de Participants
 EL SECRETO DE LA INICIACIÓN 
 Procesos Secretos del Alma 
 Estructura Secreta del Ritual Masónico 
 Los extraños Ritos de Sangre 
 Cámara de Reflexiones 
 
 
  Eines
 
General: ARCO DEL TRIUNFO DE PARIS, DISEÑADO EN FUNCION A LA ESTRELLA SIRIO
Triar un altre plafó de missatges
Tema anterior  Tema següent
Resposta  Missatge 1 de 87 del tema 
De: BARILOCHENSE6999  (Missatge original) Enviat: 06/02/2015 01:09
That's right: Sirius rises at 26 degrees south of east, or bearing 116 degrees, from the latitude of Paris, and this is the direction in which the Champs Elysées is aligned.



The Champs Elysées. The name is French for "Elysian Fields":

Quote:
Elysium or the Elysian Fields (Ancient Greek: Ἠλύσιον πεδίον, Ēlýsion pedíon) is a conception of the afterlife that evolved over time and was maintained by certain Greek religious and philosophical sects, and cults. Initially separate from the realm of Hades, admission was initially reserved for mortals related to the gods and other heroes. Later, it expanded to include those chosen by the gods, the righteous, and the heroic, where they would remain after death, to live a blessed and happy life, and indulging in whatever employment they had enjoyed in life.
Remember how the novel Arch of Triumph 1948 describes the Arc de Triomphe?: as the "huge gate to Hades"

Now, the star Sirius, which is the star associated with Isis, rises from Paris every day at 116 degrees, but it does so at a different time each day.

On August 31 each year, and on August 31 1997, Sirius rises about 5:30am. That means that if you had stood in the Champs Elysées and sighted along the avenue, before dawn on the morning that Diana died, you would see this sight: or at least, this is a version of what it would look like stitched together out of Google earth and Stellarium.



I got a bit more creative:



Then, a few minutes later, the moon rose, though it was almost imperceptible. Nevertheless it was there: so this was the scene in the skies to the east of Paris, literally as the official announcement of the death of Diana was made. Sirius rising through the Arc de Triomphe and along the Champs Elysées, and the moon further to the north, breaking the horizon within minutes. The moon, Diana, and Sirius, Isis, hovering over the city waking up to the news.



So how is Diana equal to Isis, or Sirius?

Diana was born with the sun conjunct Sirius. Her astrology chart for those of you who are happy with that kind of thing, is here. Her natal sun is at 9 degrees 40 minutes of Cancer, and Sirius is at 13 degrees 32 minutes of Cancer, which is within the orb of a conjunction.

So Diana's sun at birth is conjunct Sirius!

Now this is true for any one who is born on July 1, or a day or two either side. Like Charles Laughton. Anyone with a July 1 birthday is a fitting archetype, potentially, for Isis, as their sun, or individuality, aligns with that of Isis.

Diana certainly steps into her archetypes, no question of that, as the images above show, and plenty more to come on that.

There are enough clues on the table now to be able to bring some ideas into focus.

Elysian Fields. Gate to Hades. Arc de Triomphe sited on the "star", symbol of Isis. Champs Elysées aligned to the rising of Sirius=Isis. Paris as ancient temple of Isis. Isis who came to Paris on a boat. Diana, who came to Paris on a boat, whose name was changed to Osiris. The moon at it's lowest ebb, at it's darkest, at it's nadir. Death, as the moon is extinguished.

And then rebirth, as Sirius rises above the horizon, reborn, through the gates, the portals, of the Arch of Triumph.

This is a ritual, a theatrical presentation, a play that runs without a script yet everything, somehow, happens right on cue. Down to the minute. Yet it seems to resonate across the centuries, even the millennia...
 


Primer  Anterior  73 a 87 de 87  Següent   Darrer  
Resposta  Missatge 73 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 16/01/2025 14:14
The obelisks and domes at the Vatican and Washington DC are aligned to exactly 88.88 degrees. There’s another city that has a famous dome, can you guess which one it is…?
The Vatican and Washington obelisks and domes… The obelisks and domes at the Vatican and Washington DC are aligned to exactly 88.88 degrees. There’s another city that has a famous dome, can you guess which one it is…?
The Vatican and Washington obelisks and domes… The obelisks and domes at the Vatican and Washington DC are aligned to exactly 88.88 degrees. There’s another city that has a famous dome, can you guess which one it is…?
That’s St Paul’s Cathedral, which stands at the heart of the City of London, England:
That’s St Paul’s Cathedral, which stands at the heart of the City of London, England:
That’s St Paul’s Cathedral, which stands at the heart of the City of London, England:
 
So, now that you’ve been introduced to Washington D.C., Vatican City, and the City of London, can you guess what else they all have in common? Here’s a clue: The answer is that they are all independent city-states…
So, now that you’ve been introduced to Washington D.C., Vatican City, and the City of London, can you guess what else they all have in common? Here’s a clue: The answer is that they are all independent city-states…
•Vatican City – officially not part of Italy •City of London – officially not part of England •Washington D.C. – officially not part of USA Together, they form a trinity of global control in finance, military, and religion.
•Vatican City – officially not part of Italy •City of London – officially not part of England •Washington D.C. – officially not part of USA Together, they form a trinity of global control in finance, military, and religion.
Just like Washington DC and Vatican City, London has its very own obelisk too. Cleopatra’s Needle stands on the embankment on the Thames river:
Just like Washington DC and Vatican City, London has its very own obelisk too. Cleopatra’s Needle stands on the embankment on the Thames river:
The obelisk is inscribed with hieroglyphs, and comes with its very own sphinx’s too:
The obelisk is inscribed with hieroglyphs, and comes with its very own sphinx’s too:
The obelisk is inscribed with hieroglyphs, and comes with its very own sphinx’s too:
This exact obelisk was first erected in Heliopolis, Egypt, before being moved to London on 22/2 1881, as per the plaque on its base:
This exact obelisk was first erected in Heliopolis, Egypt, before being moved to London on 22/2 1881, as per the plaque on its base:
 
Imagine the effort required to move a 69ft (21m) statue weighing 224 tons, especially in 1881… there must have been a very important reason for it!
Imagine the effort required to move a 69ft (21m) statue weighing 224 tons, especially in 1881… there must have been a very important reason for it!
Though they form power centers encompassing finance, military, and religion, London, Washington DC, & the Vatican aren’t the only places showcasing Osiris’s manhood out in the open…A 75ft (23m) obelisk that originally stood in Luxor, Egypt now stands at the center of
of Place de la Concorde in Paris:
of Place de la Concorde in Paris:
of Place de la Concorde in Paris:
of Place de la Concorde in Paris:
It must be pretty important if it gets to stand at the very center of such an important square aligned to the Arc de Triomphe…Note the golden capstone by the way…
It must be pretty important if it gets to stand at the very center of such an important square aligned to the Arc de Triomphe…Note the golden capstone by the way…
For anyone that is wondering, the exact alignment between this obelisk and the Arc de Triomphe is 116.00 degrees.
For anyone that is wondering, the exact alignment between this obelisk and the Arc de Triomphe is 116.00 degrees.
Not to be outdone by the Brits, Americans, and French, ze Germans got an obelisk too… Schoppenhauserstrasse, Berlin:
Not to be outdone by the Brits, Americans, and French, ze Germans got an obelisk too… Schoppenhauserstrasse, Berlin:
Not to be outdone by the Brits, Americans, and French, ze Germans got an obelisk too… Schoppenhauserstrasse, Berlin:
The Italians clearly love a good obelisk too it seems… Piazza Navona, Rome:
The Italians clearly love a good obelisk too it seems… Piazza Navona, Rome:
 
and so does everybody else around the world…São Paulo, Brazil~ Buenos Aires, Argentina Hyde Park, Sydney Lisbon, Portugal Kofu, Japan, Istanbul, Turkey Stockholm, Sweden Dublin, Ireland Madrid, Spain
and so does everybody else around the world…São Paulo, Brazil~ Buenos Aires, Argentina Hyde Park, Sydney Lisbon, Portugal Kofu, Japan, Istanbul, Turkey Stockholm, Sweden Dublin, Ireland Madrid, Spain
and so does everybody else around the world…São Paulo, Brazil~ Buenos Aires, Argentina Hyde Park, Sydney Lisbon, Portugal Kofu, Japan, Istanbul, Turkey Stockholm, Sweden Dublin, Ireland Madrid, Spain
and so does everybody else around the world…São Paulo, Brazil~ Buenos Aires, Argentina Hyde Park, Sydney Lisbon, Portugal Kofu, Japan, Istanbul, Turkey Stockholm, Sweden Dublin, Ireland Madrid, Spain
So what’s the story behind all these obelisks then? Here’s the  the story about Osiris and his phallus…(remember the golden capstone in Paris…)
So what’s the story behind all these obelisks then? Here’s the  the story about Osiris and his phallus…(remember the golden capstone in Paris…)
So what’s the story behind all these obelisks then? Here’s the  the story about Osiris and his phallus…(remember the golden capstone in Paris…)
Clearly, with a story like that it makes perfect sense that every major city wants to have its own version of Osiris’ manhood erected in city squares and plazas… Or not…
Whatever the myth says about Osiris, we can clearly conclude that ancient Egyptian influence and Osiris worship goes far and wide, even in our modern day and age. Now, lets look at another perhaps more modern obelisk…
Whatever the myth says about Osiris, we can clearly conclude that ancient Egyptian influence and Osiris worship goes far and wide, even in our modern day and age. Now, lets look at another perhaps more modern obelisk…
Might be worth taking a closer look at the new WTC…TBC…
One World Freedom Tower, New York The tower was officially opened on November 3rd, 2014. That date is 11/3 in the US; ???? keep that date/number in mind. Looking at the towers architectural shape, we see its design is that of a square anti-prism:
One World Freedom Tower, New York The tower was officially opened on November 3rd, 2014. That date is 11/3 in the US; ???? keep that date/number in mind. Looking at the towers architectural shape, we see its design is that of a square anti-prism:
When viewed from street level the tower resembles a pyramid with a capstone:
When viewed from street level the tower resembles a pyramid with a capstone:
 
You may have seen this pyramid elsewhere, such as on the back of a one dollar bill: One dollar bill…  One World Trade Center… both used for trade. Notice the eye at the top of the dollar pyramid?
You may have seen this pyramid elsewhere, such as on the back of a one dollar bill: One dollar bill…  One World Trade Center… both used for trade. Notice the eye at the top of the dollar pyramid?
You may have seen this pyramid elsewhere, such as on the back of a one dollar bill: One dollar bill…  One World Trade Center… both used for trade. Notice the eye at the top of the dollar pyramid?
Could that be Horus/Baal/master again?…
Could that be Horus/Baal/master again?…
Could that be Horus/Baal/master again?…
You may also have noticed a rather large pyramid in London, also furnished with its very own capstone…
You may also have noticed a rather large pyramid in London, also furnished with its very own capstone…
The Shard is often (jokingly) referred to as Sauron’s all-seeing eye due to its uncanny resemblance to the tower in The Lord of the Rings. Note that the top part of the tower pyramid is frequently lit up at night… like a pyramid with a capstone:
The Shard is often (jokingly) referred to as Sauron’s all-seeing eye due to its uncanny resemblance to the tower in The Lord of the Rings. Note that the top part of the tower pyramid is frequently lit up at night… like a pyramid with a capstone:
Speaking of Sauron, here’s some quick comic relief for those who need it:  ???? youtu.be
 
As you can see below those two aren’t the only modern pyramid structures around, but I’ll let you research those further on your own for atlasobscura.com
As you can see below those two aren’t the only modern pyramid structures around, but I’ll let you research those further on your own for
 
Now, moving on from obelisks and pyramids… As we’ve had a very brief look at the backside of the one dollar bill, lets do the same on the front shall we!
Now, moving on from obelisks and pyramids… As we’ve had a very brief look at the backside of the one dollar bill, lets do the same on the front shall we!
 
George Washington must have been a pretty important chap if he’s on the front of the dollar bill… “Freemason… and First President”… nice to see that he got his priorities straight on the statue below! Remember that golden statue at the New York Grand Lodge too.
George Washington must have been a pretty important chap if he’s on the front of the dollar bill… “Freemason… and First President”… nice to see that he got his priorities straight on the statue below! Remember that golden statue at the New York Grand Lodge too.
George Washington must have been a pretty important chap if he’s on the front of the dollar bill… “Freemason… and First President”… nice to see that he got his priorities straight on the statue below! Remember that golden statue at the New York Grand Lodge too.
George Washington must have been a pretty important chap if he’s on the front of the dollar bill… “Freemason… and First President”… nice to see that he got his priorities straight on the statue below! Remember that golden statue at the New York Grand Lodge too.
I s

Resposta  Missatge 74 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 16/01/2025 14:14
howed you the 88.88 alignment between the Washington monument (Osiris’s phallus) and the Capitol building (Isis’ womb), which matched the 88.88 alignment at the Vatican. Care to guess which year the Washington Monument was opened?…
I showed you the 88.88 alignment between the Washington monument (Osiris’s phallus) and the Capitol building (Isis’ womb), which matched the 88.88 alignment at the Vatican. Care to guess which year the Washington Monument was opened?…
The Washington Monument was opened on October  9th, 1888… there are those 8’s again! Incidentally that was exactly one month after Easter Island was annexed (Sept. 9th, 1888).
Also note that the area of the grass surrounding the Washington Memorial is 106.01 acres. Remember the 1,016ft tall Shard and the 116.00 degree alignment in Paris? These are the same digits.
Also note that the area of the grass surrounding the Washington Memorial is 106.01 acres. Remember the 1,016ft tall Shard and the 116.00 degree alignment in Paris? These are the same digits.
Here’s another coincidence: The river flowing through Vatican City is the Tiber River: Did you know that Washington DC had a creek by the same name until the 1800’s?
Here’s another coincidence: The river flowing through Vatican City is the Tiber River: Did you know that Washington DC had a creek by the same name until the 1800’s?
Here’s another coincidence: The river flowing through Vatican City is the Tiber River: Did you know that Washington DC had a creek by the same name until the 1800’s?
Tiber Creek was used as a channel while the city plan was being built. Given that the creek shares the same name as the river at the Vatican, and that the Vatican also lines up to 88.88, it is obvious that the designers of Washington D.C. had a connection to the Vatican.
Tiber Creek was used as a channel while the city plan was being built. Given that the creek shares the same name as the river at the Vatican, and that the Vatican also lines up to 88.88, it is obvious that the designers of Washington D.C. had a connection to the Vatican.
Tiber Creek was used as a channel while the city plan was being built. Given that the creek shares the same name as the river at the Vatican, and that the Vatican also lines up to 88.88, it is obvious that the designers of Washington D.C. had a connection to the Vatican.
Drum ???? roll plz…They designed an upside down pentagram, the base of which is at the White House:
Drum ???? roll plz…They designed an upside down pentagram, the base of which is at the White House:
Drum ???? roll plz…They designed an upside down pentagram, the base of which is at the White House:
 
The White House itself is at the center of a Templars Cross:
The White House itself is at the center of a Templars Cross:
The White House itself is at the center of a Templars Cross:
The Templar’s Cross is clearly a key symbol at the Vatican judging by what the Pope is wearing…
The Templar’s Cross is clearly a key symbol at the Vatican judging by what the Pope is wearing…
The Templar’s Cross is clearly a key symbol at the Vatican judging by what the Pope is wearing…
The city plan also includes a 6-pointed star (no, this is not the star of David!), with its base at the US Capitol. I will cover this 6-pointed star in great depth in a later post because it is hugely significant.
The city plan also includes a 6-pointed star (no, this is not the star of David!), with its base at the US Capitol. I will cover this 6-pointed star in great depth in a later post because it is hugely significant.
The city plan also includes a 6-pointed star (no, this is not the star of David!), with its base at the US Capitol. I will cover this 6-pointed star in great depth in a later post because it is hugely significant.
Do you remember the masonic emblem? Notice the square and compass in the middle:
Do you remember the masonic emblem? Notice the square and compass in the middle:
The square and compass are also included in Washington DC’s street map:
The square and compass are also included in Washington DC’s street map:
The square and compass are also included in Washington DC’s street map:
The House of the Temple, the headquarters of the Scottish Rite of Freemasonry (i.e. Home of The Supreme Council of the 33°*)?
the One World Freedom Tower opened on 11/3 (i.e. November 3rd)… 11×3=33… Which as  you can see by the fact that the Freemasons have 33 degrees is a pretty significant number. You’re going be seeing plenty more of 33 (and 13 for that matter) in the future…
the One World Freedom Tower opened on 11/3 (i.e. November 3rd)… 11×3=33… Which as  you can see by the fact that the Freemasons have 33 degrees is a pretty significant number. You’re going be seeing plenty more of 33 (and 13 for that matter) in the future…
 
As I can’t help myself, here‘s a quick example for you – pay attention to the date! en.wikipedia.org
As I can’t help myself, here‘s a quick example for you – pay attention to the date!
 
The House of the Temple is located exactly 1 mile directly north of the White House:
The House of the Temple is located exactly 1 mile directly north of the White House:
The Lincoln Memorial and Jefferson Memorial also share a special alignment…
The Lincoln Memorial and Jefferson Memorial also share a special alignment…
The Lincoln Memorial and Jefferson Memorial also share a special alignment…
… They line up to the Winter Solstice:
… They line up to the Winter Solstice:
And lest we forget there’s also the Pentagon, the military arm of the control trinity:
And lest we forget there’s also the Pentagon, the military arm of the control trinity:
Here we see it all come together nicely: Note that the US Capitol, White House, Jefferson Memorial, and Lincoln Memorial form an upside down cross.
Here we see it all come together nicely: Note that the US Capitol, White House, Jefferson Memorial, and Lincoln Memorial form an upside down cross.
Want to know where else we can find an upside down cross? Yes, that is the Pope, sitting on a throne with an upside down cross.
Want to know where else we can find an upside down cross? Yes, that is the Pope, sitting on a throne with an upside down cross.
Want to know where else we can find an upside down cross? Yes, that is the Pope, sitting on a throne with an upside down cross.
 
And here he is on his (very picturesque) Papal Throne… just lovely isn’t it? Pope Benedict XVI (C) waves to the faithful, flanked by Archbishop James Michael Harvey (L) and his personal secretary Georg Genswein (R), during his weekly Wednesday general audience at Paul VI Hall at
And here he is on his (very picturesque) Papal Throne… just lovely isn’t it? Pope Benedict XVI (C) waves to the faithful, flanked by Archbishop James Michael Harvey (L) and his personal secretary Georg Genswein (R), during his weekly Wednesday general audience at Paul VI Hall at
the Vatican August 24, 2005. REUTERS/Alessandro Bianchi.
As if things couldn’t get any weirder, let me introduce you to…   The Owl You may have noticed that there was something funny about the layout around the US Capitol building…
As if things couldn’t get any weirder, let me introduce you to…   The Owl You may have noticed that there was something funny about the layout around the US Capitol building…
As if things couldn’t get any weirder, let me introduce you to…   The Owl You may have noticed that there was something funny about the layout around the US Capitol building…
As if things couldn’t get any weirder, let me introduce you to…   The Owl You may have noticed that there was something funny about the layout around the US Capitol building…
The owl is also hiding on the dollar bill…
The owl is also hiding on the dollar bill…
Owls continued ~
https://en.rattibha.com/thread/1573482371160088578

Resposta  Missatge 75 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 16/01/2025 15:52

Resposta  Missatge 76 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 16/01/2025 16:39
Bretton Woods System. - ppt video online download

Resposta  Missatge 77 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 17/01/2025 23:28

Escalera de caracol dentro del arco del triunfo París Francia - Foto de stock

 
Escalera de caracol dentro del arco del triunfo París Francia - Foto de stock de Arco del Triunfo - París libre de derechos

Resposta  Missatge 78 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 18/01/2025 00:29
Sunset under the Arc de Triomphe © Siren-Com - licence [CC BY-SA 3.0] from Wikimedia CommonsSunset under the Arc de Triomphe © Siren-Com – licence [CC BY-SA 3.0] from Wikimedia Commons

The sun sets on the Historical Axis several times in a year:

  • It sets towards the West under the arch on 6 occasions: on the 7th, 8th and 9th May and on the 3rd, 4th and 5th August (from place de la Concorde)
  • The sun rises towards the East under the arch 4 times each year: on the 4th, 5th and 6th February and on the 7th November (from Porte Maillot).

Resposta  Missatge 79 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 20/01/2025 04:46
Poésie nocturne : Paris de nuit, depuis Montmartre, France (en haut, à gauche, l’étoile Sirius), 29 décembre 2013 (22 h 28)

  

Paris de nuit, depuis Montmartre, France (en haut, à gauche, l'étoile Sirius)
Tableau hors cadre numéro 130, le 29 décembre 2013 (22 h 28

Resposta  Missatge 80 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 20/01/2025 05:06

Calcul du diamètre de Sirius

Si nous savons aujourd'hui que le Soleil est une étoile, il n'en a pas toujours été ainsi. L'écart de luminosité est tel qu'il était, en effet, bien difficile à nos ancêtres  d'imaginer que les pointes de  lumière qui parsèment  le ciel nocturne n'étaient rien  d'autres que des soleils tout à fait  comparables au nôtre.

La raison de cette différence ? Les distances extraordinaires, hors de toute échelle humaine, qui nous séparent des étoiles. Mais comment les appréhender et  les mesurer précisément ?

De nos jours encore, calculer  les  distances, les dimensions, et plus généralement, se faire une idée des ordres de grandeur reste l'une des tches principales des astronomes. Peut-on vraiment parler d'une galaxie sans d'abord faire référence à son immensité ?  Comment expliquer le fonctionnement d'une étoile sans évoquer sa masse gigantesque qui comprime la matière en son coeur jusqu'à lui permettre de fusionner ?

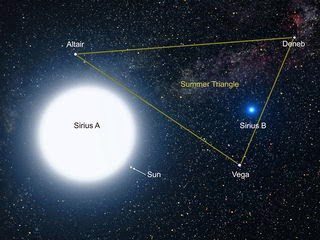
 C'est à ce petit jeu des mesures que je vous convie aujourd'hui, en vous proposant, par le calcul, de découvrir comment il est possible d'estimer  le diamètre de  Sirius, l'étoile la plus brillante du ciel.

En montrant qu'une étoile et le Soleil sont de dimension comparable, on dispose d'un élément important pour  comprendre que ce sont des astres de même nature. Au dix-neuvième siècle, la spectroscopie en prouvant l'identité de leur composition est venue confirmer l'hypothèse.

 Ce calcul est, sinon plus difficile, du moins peut-être un peu plus long que ceux déjà publiés sur ce site. Il suppose un minimum de connaissances en astronomie.

 _________________________________________________________

 

Voici les données dont nous disposons :

 

. magnitude visuelle apparente de Sirius  : mSir  :  -  1,43

. Magnitude visuelle absolue du Soleil      : MSol :  + 4,83

. Corrections bolométriques : Sirius : - 0,64  ,   Soleil : - 0,11

. Parallaxe de Sirius              : 0,371"  (secondes d'arc)

. Diamètre du Soleil : 1 392 000 kilomètres,  soit 1,392 x 109 mètres

. Estimation des températures de surface :

                                     pour le Soleil : TSol =  5 850 K

                                     pour Sirius     : TSir  =  9 230 K

_________________________________________________________

 

Principales étapes du calcul :

 

1 : Nous calculerons  la Magnitude absolue de Sirius. Elle sera déterminée à partir de la magnitude apparente (connue) et de la distance que nous estimerons via la parallaxe.

2 : Nous déterminerons le rapport de luminosité (éclat) des deux étoiles, (c'est à dire de combien Sirius est plus brillante que le Soleil).

3 : Puis, connaissant les températures de surfaces du Soleil et de Sirius, nous comparerons  le rayonnement par unité de surface de ces deux astres (nous verrons ainsi de combien, pour une surface donnée,  Sirius est plus brillante que le Soleil).

4 : Enfin, en comparant les magnitudes absolues des deux étoiles pondérées de leur luminosité surfacique nous déterminerons le rapport de surface des deux astres et par là leur rapport de taille et donc le diamètre absolu de Sirius(la taille du Soleil étant connue). Nous en déduirons aussi le diamètre apparent (angulaire) de Sirius.

5 : Nous comparerons ces résultats à des mesures faites au VLT afin de vérifier leur vraisemblance.

6 : Afin de  fixer les idées et les ordres de grandeur dans l'Univers, nous verrons ensuite à quelle distance il faudrait situer une pièce de un euro pour qu'elle apparaisse sous le même diamètre angulaire  que Sirius.

note :  Tous les logarithmes utilisés au cours de ces calculs sont  décimaux.

_________________________________________________________

 

1 Détermination de la Magnitude Absolue de Sirius.

 

a , calcul de la distance de Sirius

Rappel : Le (ou la) parallaxe d'une étoile est  la mesure angulaire de son déplacement apparent sur la voute céleste lorsque l'observateur (sur Terre en général) se déplace de une unité astronomique selon un axe perpendiculaire à la ligne de visée. Le rapport (1 / parallaxe (en secondes d'arc)) donne la distance de l'étoile en parsecs.  

Parallaxe de Sirius : 0,371"

Donc, distance de Sirius (en parsecs) = 1 / 0,371 = 2,695 Parsecs

Soit en mètres :  3,086 x 1016 m x 2,695 =  8,317 x 1016 m, c'est à dire un peu plus de 80 000 milliards de kilomètres ou environ 8,8 années lumière.

 

b, calcul de la Magnitude Absolue visuelle de Sirius (Msir)

Rappel : Le Module de distance  est la différence (m - M) entre les magnitudes apparentes et absolues. Par construction  il s'annule quand un astre est situé à 10 parsecs, à cette distance, les deux magnitudes sont égales.  (Pour plus d'informations sur ce point voir module de distance et magnitude).  

La formule liant  distance et module de distance est :

  m - M = 5 log  d - 5                              

En remplaçant m et d par leurs valeurs pour Sirius, nous obtenons :

       - 1,43  -  M  =   5 log 2,695  -  5  

En remplaçant log  2,695 par sa valeur : (0,431)

        - 1,43  -  M  =    5 x 0,431  - 5

        - 1,43  -  M  =    2,153 - 5

                    -  M  =    2,153 - 5 +1,43

                    -  M  =    2,153 - 3,570

                    -  M  =  - 1,417

                              M  =    1,417 soit, en arrondissant :

                       MSirius   =   1,42 

 

c, calcul des Magnitudes Absolues Bolométriques de Sirius et du Soleil

Rappel : La magnitude bolométrique (qu'elle soit absolue ou apparente) est la mesure de la lumière reçue d'une étoile en intégrant le rayonnement dans toutes les longueurs d'ondes. Ce rayonnement est donc plus fort que dans le seul domaine visible. Comme l'échelle des magnitudes est inversée, le passage de la magnitude visuelle à la magnitude bolométrique nécessite l'ajout d'une valeur négative appelée correction bolométrique (CB). Des tables donnent la valeur de cette correction qui diffère selon la température de l'étoile (et donc sa couleur dominante). Plus une étoile s'éloigne de l'astre de référence (Type stellaire F5 ayant une température de surface de 6 500 K et pour laquelle CB =0) ) plus la correction bolométrique est importante parce qu'une partie de son rayonnement se situe hors du domaine de mesure des magnitudes visibles. Ce manque peut se situer  vers l'infrarouge pour les étoiles froides ou vers l'ultraviolet pour les étoiles chaudes.

 

De façon générale :                 Mbol = M visuelle + BC

 

Comme les corrections bolométriques pour Sirius et pour le Soleil sont respectivement - 0,64 et - 0,11  nous obtenons :

 

                                             M bol Sirius = 1,42 - 0,64 = 0,78

                                             M bol Soleil = 4,83 - 0,11 = 4,72

 

2, Comparaison des luminosités des deux astres

Rappel : La relation entre les rapports d'éclat absolu ( E : mesure de la puissance du rayonnement de l'étoile) et la différence de Magnitude absolue ( M : mesure de cette puissance dans le système des magnitudes) de deux astres A et B est donnée par la formule dite de Pogson qui s'écrit : 

 

                                M (A) -  M (B)   =  - 2,5 log ( E(A) / E(B)  )

Rem : La formule serait identique si nous comparions éclat apparent et magnitude apparente. D'autre part,  nous utiliserons désormais pour la suite des calculs les Magnitudes absolues bolométriques déterminées plus haut sans systématiquement rappeler leur caractère bolométrique dans les notations). 

 

Ainsi dans notre cas :  (A est  identifié à Sirius et B au Soleil)

                   M (Sirius) -   M (Soleil)   =   - 2,5 log (E(Sirius) / E (Soleil) )

En remplaçant par les valeurs données ou trouvées ci-dessus :

          0,78 - 4,72    = - 2,5 log (E (Sirius) / E (Soleil) )

                   - 3,94    = - 2,5 log (E (Sirius)  / E (Soleil) )

           -3,94 / - 2,5   =  log   (E (Sirius)  / E (Soleil) )                                       

                     1,576   =  log  (E (Sirius)  / E (Soleil) )

En mettant 10 à la puissance des deux termes de l'équation :

                      101,576  = 10 log (E(Sirius) / E (Soleil)  )

En remplaçant 101,576 par sa valeur : 37,67

                       37,67    = 10 log (E(Sirius) / E (Soleil)  )

 Comme 10log a redonne a :   (a étant identifié à : E (Sirius) / E (Soleil) )

                       37,67 = Eclat de Sirius / Eclat du Soleil

 

Toute longueurs d'ondes confondues, Sirius est donc près de 38 fois plus lumineuse que le Soleil !

 

3, Comparaison  de la luminosité  surfacique de Sirius et du Soleil

Rappel :  la luminosité d'un corps est proportionnelle à la puissance quatrième de sa température de surface (en K) ainsi qu' à sa surface (en mètres carrés). La relation entre rayonnement, température et surface est donnée par la formule dite de Stephan qui s'écrit : L =  s S T 4  )  L étant la luminosité (en watts) et s la constante de Stephan , nous n'avons pas besoin ici de cette formule mais pour voir un exemple d'utilisation, consulter l'article: De combien nous réchauffe l'Effet de Serre ? . 

 

T° Sirius  =  9 230 K,    T° Soleil  =  5 850 K

Le rapport des deux températures de surface est donc de  :

                         9 230 K / 5 850 K = 1,578

La luminosité étant proportionnelle à la puissance quatrième de la température,  pour une surface donnée, Sirius rayonne 1,5784 fois plus que le Soleil, soit :

                         1,5784 = 6,197

Remarque : A cause de cet élément en puissance 4, la précision du résultat est très fortement dépendante de la précision des mesures de température des deux étoiles. Un faible écart sur ce point peut donner un résultat sensiblement différent. Ces températures sont estimées par spectroscopie ( loi de Wien et plus fondamentalement de Plank)

 

4, Détermination du diamètre de Sirius. 

 

a, calcul du diamètre de Sirius

 

Sirius rayonne globalement 37,67 fois plus que le Soleil mais par unité de surface elle rayonne 6,19 fois plus (du fait de sa température plus élevée).

Sa surface est donc 37,67 / 6,19 fois plus grande que celle de notre Soleil.

                        37,67 / 6,19  =  6,09.

Comme une surface d'un corps est proportionnelle au carré de sa taille, cette taille elle-même est proportionnelle à la racine carrée de sa surface. 

Le diamètre de Sirius est donc égal à racine carrée de 6,09 (fois celui du Soleil)

                        6,091/2   =    2,47

Sirius est 2,5 fois plus grande que notre Soleil, celui-ci ayant un diamètre de 1 392 000 kilomètres, Le diamètre de Sirius est donc de :

                        1 392 000  x  2,47  =  3 438  240  kilomètres

Une telle précision est évidemment illusoire, retenons comme résultat de notre estimation :

 

Diamètre de Sirius : 3 400 000 kilomètres 

 

b, calcul du diamètre apparent de Sirius

Pour de petits angles, c'est le cas ici,  le diamètre angulaire d'un objet exprimé en radian est égal au ratio : Diamètre / Distance (de cet objet par rapport à l'observateur).

En remplaçant le diamètre et la distance par leurs valeurs,  respectivement 3,4 x109 m  et 8,317 x 1016 m, nous obtenons le diamètre angulaire de Sirius qui vaut donc : 

               3,4 x 109 m /  8,317 x 1016 m  =  4,088 x 10-8 radians. 

 

Un radian correspondant à 206 264,8 secondes d'arc (")

Le diamètre de apparent de Sirius dans le ciel est de :

               4,088 x 10-8  x  206 264,8"  =  0, 008 43 "

Il s'agit là d'un angle infime. Une seconde d'arc (notée ") correspond à un 3 600ème de degré et  donc 0,008 "  (moins de un centième de seconde) représente seulement un 450 000ème de degré.

 

5,  Comparaison avec les mesures effectuées au VLT

 

En 2001, une campagne de mesures a été menée au Very Large Telescope (VLT) en utilisant les techniques d'interférométrie. Compte tenu de la petitesse angulaire des étoiles vues depuis la Terre, très peu d'astres sont susceptibles de faire l'objet de telles mesures.

 

Pour Sirius on a trouvé un diamètre  de 0,009 29 secondes d'arc (+/- 0,000 17") soit en radians :  0,009 29 / 206 264,8   = 4,5 x 10-8 radians  

A partir de cette mesure nous pouvons déduire le diamètre effectif de Sirius  

En remplaçant la distance par sa valeur : (8,317 x 1016 m) dans l'équation : (diamètre / distance) = angle (si exprimé en radians), nous obtenons:

Diamètre de Sirius (m) / 8,317 x 1016 (m) =  4,5  x 10-8

Diamètre de Sirius (m)  = 4,5 x 10-8 x 8,317 x 1016 m = 3,743 x 109 m

 

Diamètre de Sirius = 3,7 millions de kilomètres (Valeur arrondie)  

 

Cette valeur est assez proche de celle que nous avions calculée (3,4 millions de kilomètres), puisque l'écart est d'environ 10 %. Notre estimation était donc parfaitement vraisemblable.  Beaucoup de données en astronomie ne sont d'ailleurs pas connues avec une telle précision. Notre petit calcul permet donc déjà d'établir un ordre de grandeur tout à fait respectable.

 

6,  A quoi correspond un tel diamètre ?

 

Pour se faire une idée de ce que représentent ces ordres de grandeur, assimilons Sirius à un objet de la vie courante, une pièce de un euro par exemple.

A quelle distance faudrait-il placer une pièce de un euro pour qu'elle occupe dans le ciel un angle comparable à celui de Sirius ?  

Il suffit de résoudre l'équation égalisant les  ratios: diamètre / distance pour chacun des deux objets: c'est à dire trouver DP  (Distance de la Pièce, en mètres) dans l'équation suivante :

Diamètre de Sirius / Distance de Sirius = Diamètre de la Pièce / DP

 

Pour le diamètre de Sirius, retenons les données du VLT.

Diamètre de Sirius = 3,750 x 109 m

Distance de Sirius  = 8,317 x 1016 m

Diamètre d'une pièce de un euro  = 23,25 mm soit : 2,325 x 10-2 m

Distance de cette pièce = DP (l'inconnue recherchée)

          (3,750 x 109 / 8,317 x 1016 )  = 2,325 x 10-2 / DP

          (3,750 x 109  / (8,317x 1016 x 2,325 x 10-2) ) = 1/DP

          (3,750 x109  / 1,933 x 1015)   =  1 / DP 

           1,933 x 1015 / 3,750 x 109    =  DP

           1,933 x 1015-9 / 3,750            =  DP

            0,515 x 106        =   DP

           5,150 x 105        =   DP

 

           Distance de la Pièce =  515 000 mètres soit 515 kilomètres.

 

Il faudrait donc placer une pièce de un euro à 515 kilomètres de l'observateur  pour qu'elle présente le même diamètre apparent que Sirius vue de la Terre (c'est approximativement la distance qui sépare Paris de Montélimar à vol d'oiseau). Pour que sa luminosité soit équivalente il faudrait également la chauffer à 9 230 K (ce qui ne serait pas facile, de plus, à une telle température, la pièce se trouverait gazéifiée !)

Ainsi, les étoiles, malgré leurs dimensions gigantesques, ne représentent que d'infimes îlots de matière perdus dans notre galaxie, la Voie Lactée. Sirius est pourtant parmi les plus proches.

http://lesetoiles.over-blog.net/article-calcul-du-diametre-de-l-etoile-sirius-56378672.html

Resposta  Missatge 81 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 20/01/2025 05:46

SECRETS THAT SURROUND US

Placeholder Picture

The crisp autumn air saunters across the cobblestones of the courtyard lit by the warm glow from gas lamps. Nestled in a horseshoe of majestic Baroque buildings, the modern glass pyramid of the Musee´de Louvre seems both incongruous and yet oddly at home amid the splendour of the surrounding 17th century architecture. In one moment the ancient and the modern rub shoulders as if suggesting a continuity of some grand purpose. Indeed, to stand in front of this diamond of glass and steel is to experience first-hand the implementation of ageless knowledge, perpetuated through adepts in secret societies dating back to the Egyptian Mysteries schools, whose original purpose was— and remains— the continuous promulgation of a secret science of life that serves the highest principles of humanity.

The controversial pyramid was commissioned by then president François Mitterrand, a leader sympathetic to the ideals of Masonic orders, and designed by the Chinese-American architect I.M. Pei. Although Pei stated publicly that his pyramid had nothing to do with stone pyramids of old, of all the pyramids in the world he could have used for inspiration, including their myriad angles of inclination, he chose to incline his magnum opus to within a degree of the angle used to construct the Great Pyramid of Giza: an extraordinary coincidence for a man who claimed his design had been inspired by a trellis in the nearby Jardin des Tuilleries.

Such ‘coincidences’ are the stuff of conspiracies; an excuse to point accusatory fingers at secret societies. In this case such claims are justifiable, although the motive is far from sinister. The Great Pyramid of Giza— as well as other identical structures— were built primarily by adepts who learned a specific type of craft from ancient Mysteries Schools. The keepers of an unspecified, arcane knowledge, these societies were careful with whom they shared such information lest it be misused against people or planet. The strategically-chosen slope angle of the Great Pyramid is a good example of the craft they taught.

 

One of the reasons why this most perfect of structures generates such a profound effect is due in part to its heptagonal angle, for it amplifies the energy of the most mystical of all sacred geometric shapes in the corpus sanctum of esoteric societies. The pyramid’s seven-fold geometry is an allegory of the prime notes of music and the visible colours of light, and thus it is associated with the creative forces of nature. Of all the sacred geometries it is the only one whose angles cannot be bisected to a whole number, so, like the nature of the soul and the origin of the universe, its properties are transcendental, it represents the search for enlightenment. It’s values are also bound within the human body. So, to work with a structure that incorporates this geometry is to magnify the potential of the creative power inside the human being. How strange, then, that these principles should find themselves embodied in this fabulous glass diamond now resting in the center of modern Paris, in the Cour Napoleon, whose namesake once spent a night in the original pyramid in Giza only to run out in the morning, berserk, and raving like a madman. Clearly that pyramid did not agree with Napoleon’s personal ideals.

To people who devote themselves to secret knowledge, such things are not so strange. The kind of gnosis learned in secret esoteric societies surrounds our everyday life to a far greater degree than people are aware. In Paris, the site of the Musee´ de Louvre is itself part of a city-wide plan that incorporates unusual deviations from standard building practice; many of its streets and monuments are also astronomically aligned. It is this perception of a ‘Great Plan’ at work that gives the centre of Paris its inherent air of connection to something far more ethereal and beyond the mundane world.

Just as with London, Washington, and the original Egyptian capital Thebes, Paris is the culmination of centuries of Freemasonic input which seeks to create the ideal ‘City of Light’ through the practical application of biogeometry (that is ‘living geometry’) and the manipulation of subtle terrestrial forces to mirror the celestial order above the city. The idea that the application of specific angles and astronomical alignments are capable of bestowing positive benefits on people and place was precisely the kind of information once zealously guarded and taught to all initiates in Mysteries schools. One of the very best examples of this living art lies in the ground plan of the temple complex at Thebes — today the twin sanctuaries of Luxor-Karnak. Among other things, this complex is aligned to the winter solstice, the time of year when the darkness of the night begins to be supplanted by the increasing light of the day. Another alignment references the heliacal rising of Sirius on June 16. Sirius was seen as the source of all ancient wisdom and the embodiment of Isis, the goddess of the sky. To reference a temple to Sirius is to imbue the temple and its pilgrims with the properties associated with that star.

That such knowledge has spread far from its Egyptian center is seen in a temple dedicated to Isis that once stood on the banks of the Seine, and which today serves as the foundation of the abbey of St. Germain des Pres, just to the south of the Louvre. This homage to the continuation of the cult of Isis even lent the name to the city which sprang from its environs, Parisis. Such solar or sky symbology was applied by esoteric societies even further north, in Britain, possibly by its local secret society, the Druids; its most famous of Britain’s rivers, the Thames, was originally consecrated to the Babylonian solar god Tammuz. It was also named the Isis, and the source of the Thames is today marked on maps as such.

 

The oldest and main axis of Paris is marked at pivotal sections by an obelisk transported from the temple of Luxor in the Place de Concorde, and by Pei’s pyramid. A second, deviated axis aligns from a strategic location in the Louvre, through the Arc de Triumphe, and along a majestic avenue named Champs-Elyseés. It is this path that gives away the purpose behind the ‘great plan’ upon which this city was designed. The so-called Fields of Elysium are a mythical location where favoured heroes are conveyed by the gods towards a place of the blessed, a state of happiness. Every August 6 the sun sets along the Champs Elyse´es, its orange orb observed through the last of Mitterrand’s grand commissions for Paris, a hollow cube named the Grande Arche. The alignment commemorates the Transfiguration of Christ, a powerful symbol of that establishes Man as a solar hero. Furthermore, the Grande Arche is itself deviated by 32 degrees to match the sunset on June 24— John the Baptist’s Day as well as the Masonic New Year; it is also the day after the Summer solstice, the moment when the light is at its peak; esoterically this moment represents the triumph of light over dark.

Coincidences abound, and yet all of them reference important moments in the machinery of the heavens that are enshrined in the literature of secret societies. The purpose behind such knowledge was to link people with Universal mechanics in a way that enhanced their well-being. That secret societies were able to maintain continuity of information is evidenced by the way that the Paris alignments precisely mirror the very same axis planned into the design of the city of Thebes, a ‘city of the Sun’. Masonic Paris, then, is a case of sacred architecture fulfilling an ancient plan, for 350 years prior to the inauguration of the Louvre pyramid the Hermetic philosopher Tommaso Campanella had announced that in Paris the world would see the reincarnation of the Egyptian City of the Sun.

These practices are still enshrined in the Freemasonic Lodges, a number of which maintain a strict oath to the spirit of ancient codes of practice and the utmost protection of secret knowledge. This very misunderstood society traces its origin through the Knights Templars— the Knights of the Temple of Solomon— to the Egyptian city of Iunnu, the “city of Light”, also called Heliopolis by the Greeks. The history of [Free] Masonry has much to do with the art of building in a physical as well as figurative sense. Well before the libraries at Alexandria, Iunnu was the highest center of learning in the ancient world, preserving the wisdom once practiced and adopted through in temples along the Nile and dating all the way back to Zep Tepi, the ‘First Time’, the post-diluvial age of the gods. After the Romans drove the gnostic schools of Egypt underground, secret societies were formed to maintain the teachings from interference by people who would misuse the information for personal gain and the subjugation of entire societies. Over the centuries the keepers of the Light have gone by various guises— Cathars, Albigencians, Bogomils, Essenes, Priory of Sion, Christian Gnostics, Rosicrucians— and whenever political times have allowed, such societies have shown their hand, and by this method the knowledge has been promulgated through Europe, resurfacing in Paris in time for the French Revolution. In fact many of the figures of the French uprising against a despot king were high-ranking Freemasons, as were the main figures who were inspired to create a new state called America.

https://invisibletemple.com/conspiracy-secret-society-encoded-information.html

Resposta  Missatge 82 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 20/01/2025 05:55

ANCIENT EGYPTIAN GEODESY - PART II

The great circle alignment from Giza to Alexandria has an azimuth of 51.85° north of due west from Giza (the same angle as the slope of the Great Pyramid). Extended beyond Alexandria, this great circle also crosses over Delphi, Rollright and Newgrange, as well as the city of London.

Map image © VectorGlobe

The azimuth of a great circle alignment from Dendera to Paris is also 51.85° north of due west.

Map image - Roger Hedin

Dendera was dedicated to Isis/Sirius. The ancient Egyptian year began on the date of the heliacal rising of Sirius in mid July. The helical rising of Sirius heralded the annual inundation of the Nile that was essential to the welfare of ancient Egypt. The axis of the temple of Isis at Dendera was aligned 20° south of due east, pointing directly at the rising point of Sirius from the latitude of Dendera.

Robert Bauval describes a number of connections between Isis/Sirius and Paris in Talisman (2004). Isis is shown riding on a boat in many ancient Egyptian drawings and carvings. At the direction of Napoleon, Sirius and a statue of Isis were added to the coat of arms for Paris shown below.

During the French revolution, a statue of Isis known as the Fountain of Regeneration was constructed on the former site of the Bastille. The engraving below commemorated this statue.

Fountain of Regeneration Engraving

The Elysian Fields is described as a place of eternal salvation in the ancient Egyptian Book of the Dead. Named after the Elysian Fields, the Champs Elysees is the main axis of Paris. The names Elysian and Elysees both suggest an association with Isis. The photograph below is facing southeast. The Arc de Triumphe is visible in the background. Beyond the Arc de Triumphe is the Louvre. The azimuth of the Champs Elysees is 26° south of due east, pointing directly at the rising point of Sirius/Isis from the latitude of Paris.

The termination point of the Champs Elysees to the northwest is the Grande Arche, in the foreground of the picture above. The axis of the Grande Arche is offset 6.33° south of the axis of the Champs Elysees. With an azimuth of just over 32° south of due east, the azimuth of the axis of the Grande Arche is the same as the azimuth of the great circle alignment from Paris to Dendera.

The Grande Arche is a nearly perfect cube with a height of 110 meters, a width of 108 meters and a depth of 112 meters. It is often described as a cube with side lengths of 110 meters. This is equal to 210 ancient Egyptian cubits:

110/210 = .5238

.5238 meters is a precise measure of the ancient Egyptian cubit, equating to 20.6222 inches, well within the ± .005 inches in Petrie's 20.62 inch measure of the ancient Egyptian cubit. Instead of the usual comparisons between the cubit and the meter of .52375/1 or .524/1, the best comparative measure may be the simple fraction of 11/21 that is suggested by the Grande Arche.

Image © Insecula.com

The sides of the Grande Arche are divided into 5 x 5 large panels and within each large panel are 7 x 7 smaller panels. Side lengths of 110 meters suggest lengths of 22 meters for the sides of the large panels with lengths of 22/7 meters for the sides of the smaller panels. The fraction 22/7 equals 3.1428, an accurate expression of π that is also found in the dimensions of the Great Pyramid. Side lengths of 210 cubits in the Grande Arche suggest lengths of 42 cubits for the sides of the large panels and 6 cubits for the sides of the smaller panels. This also shows that the relationship between the meter and the cubit is 6/π, using the measure of 22/7 for π:

21/11 = 6/π

22/7 x 21/11 = 6

The northern pyramid at Dashur, known as the Red Pyramid, was the first true (smooth sided) pyramid built in Egypt and it was the last pyramid built prior to construction of the Great Pyramid. The baselengths of the Red Pyramid are 420 cubits (220 meters) long, 20x multiples of 21/11.

Image by Jon Bodsworth

One of the oldest stone circles in England is at Rollright. The diameter of the Rollright circle is 31.4 meters, an accurate expression of π times 10 meters. Given the 6/π relationship between the meter and the cubit, the diameter of the Rollright circle is also 60 ancient Egyptian cubits.

BACK

http://home.hiwaay.net/~jalison/Art5.html

Resposta  Missatge 83 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 20/01/2025 14:55
Resultado de imagen para cydonia mars number 33

ANCIENT EGYPTIAN GEODESY - PART II

The great circle alignment from Giza to Alexandria has an azimuth of 51.85° north of due west from Giza (the same angle as the slope of the Great Pyramid). Extended beyond Alexandria, this great circle also crosses over Delphi, Rollright and Newgrange, as well as the city of London.

Map image © VectorGlobe

The azimuth of a great circle alignment from Dendera to Paris is also 51.85° north of due west.

Map image - Roger Hedin

Dendera was dedicated to Isis/Sirius. The ancient Egyptian year began on the date of the heliacal rising of Sirius in mid July. The helical rising of Sirius heralded the annual inundation of the Nile that was essential to the welfare of ancient Egypt. The axis of the temple of Isis at Dendera was aligned 20° south of due east, pointing directly at the rising point of Sirius from the latitude of Dendera.

Robert Bauval describes a number of connections between Isis/Sirius and Paris in Talisman (2004). Isis is shown riding on a boat in many ancient Egyptian drawings and carvings. At the direction of Napoleon, Sirius and a statue of Isis were added to the coat of arms for Paris shown below.

During the French revolution, a statue of Isis known as the Fountain of Regeneration was constructed on the former site of the Bastille. The engraving below commemorated this statue.

Fountain of Regeneration Engraving

The Elysian Fields is described as a place of eternal salvation in the ancient Egyptian Book of the Dead. Named after the Elysian Fields, the Champs Elysees is the main axis of Paris. The names Elysian and Elysees both suggest an association with Isis. The photograph below is facing southeast. The Arc de Triumphe is visible in the background. Beyond the Arc de Triumphe is the Louvre. The azimuth of the Champs Elysees is 26° south of due east, pointing directly at the rising point of Sirius/Isis from the latitude of Paris.

The termination point of the Champs Elysees to the northwest is the Grande Arche, in the foreground of the picture above. The axis of the Grande Arche is offset 6.33° south of the axis of the Champs Elysees. With an azimuth of just over 32° south of due east, the azimuth of the axis of the Grande Arche is the same as the azimuth of the great circle alignment from Paris to Dendera.

The Grande Arche is a nearly perfect cube with a height of 110 meters, a width of 108 meters and a depth of 112 meters. It is often described as a cube with side lengths of 110 meters. This is equal to 210 ancient Egyptian cubits:

110/210 = .5238

.5238 meters is a precise measure of the ancient Egyptian cubit, equating to 20.6222 inches, well within the ± .005 inches in Petrie's 20.62 inch measure of the ancient Egyptian cubit. Instead of the usual comparisons between the cubit and the meter of .52375/1 or .524/1, the best comparative measure may be the simple fraction of 11/21 that is suggested by the Grande Arche.

Image © Insecula.com

The sides of the Grande Arche are divided into 5 x 5 large panels and within each large panel are 7 x 7 smaller panels. Side lengths of 110 meters suggest lengths of 22 meters for the sides of the large panels with lengths of 22/7 meters for the sides of the smaller panels. The fraction 22/7 equals 3.1428, an accurate expression of π that is also found in the dimensions of the Great Pyramid. Side lengths of 210 cubits in the Grande Arche suggest lengths of 42 cubits for the sides of the large panels and 6 cubits for the sides of the smaller panels. This also shows that the relationship between the meter and the cubit is 6/π, using the measure of 22/7 for π:

21/11 = 6/π

22/7 x 21/11 = 6

The northern pyramid at Dashur, known as the Red Pyramid, was the first true (smooth sided) pyramid built in Egypt and it was the last pyramid built prior to construction of the Great Pyramid. The baselengths of the Red Pyramid are 420 cubits (220 meters) long, 20x multiples of 21/11.

Image by Jon Bodsworth

One of the oldest stone circles in England is at Rollright. The diameter of the Rollright circle is 31.4 meters, an accurate expression of π times 10 meters. Given the 6/π relationship between the meter and the cubit, the diameter of the Rollright circle is also 60 ancient Egyptian cubits.

BACK

http://home.hiwaay.net/~jalison/Art5.html

Resposta  Missatge 84 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 20/01/2025 15:10
Resultado de imagen para cydonia mars number 33

ANCIENT EGYPTIAN GEODESY - PART II

The great circle alignment from Giza to Alexandria has an azimuth of 51.85° north of due west from Giza (the same angle as the slope of the Great Pyramid). Extended beyond Alexandria, this great circle also crosses over Delphi, Rollright and Newgrange, as well as the city of London.

Map image © VectorGlobe

The azimuth of a great circle alignment from Dendera to Paris is also 51.85° north of due west.

Map image - Roger Hedin

Dendera was dedicated to Isis/Sirius. The ancient Egyptian year began on the date of the heliacal rising of Sirius in mid July. The helical rising of Sirius heralded the annual inundation of the Nile that was essential to the welfare of ancient Egypt. The axis of the temple of Isis at Dendera was aligned 20° south of due east, pointing directly at the rising point of Sirius from the latitude of Dendera.

Robert Bauval describes a number of connections between Isis/Sirius and Paris in Talisman (2004). Isis is shown riding on a boat in many ancient Egyptian drawings and carvings. At the direction of Napoleon, Sirius and a statue of Isis were added to the coat of arms for Paris shown below.

During the French revolution, a statue of Isis known as the Fountain of Regeneration was constructed on the former site of the Bastille. The engraving below commemorated this statue.

Fountain of Regeneration Engraving

The Elysian Fields is described as a place of eternal salvation in the ancient Egyptian Book of the Dead. Named after the Elysian Fields, the Champs Elysees is the main axis of Paris. The names Elysian and Elysees both suggest an association with Isis. The photograph below is facing southeast. The Arc de Triumphe is visible in the background. Beyond the Arc de Triumphe is the Louvre. The azimuth of the Champs Elysees is 26° south of due east, pointing directly at the rising point of Sirius/Isis from the latitude of Paris.

The termination point of the Champs Elysees to the northwest is the Grande Arche, in the foreground of the picture above. The axis of the Grande Arche is offset 6.33° south of the axis of the Champs Elysees. With an azimuth of just over 32° south of due east, the azimuth of the axis of the Grande Arche is the same as the azimuth of the great circle alignment from Paris to Dendera.

The Grande Arche is a nearly perfect cube with a height of 110 meters, a width of 108 meters and a depth of 112 meters. It is often described as a cube with side lengths of 110 meters. This is equal to 210 ancient Egyptian cubits:

110/210 = .5238

.5238 meters is a precise measure of the ancient Egyptian cubit, equating to 20.6222 inches, well within the ± .005 inches in Petrie's 20.62 inch measure of the ancient Egyptian cubit. Instead of the usual comparisons between the cubit and the meter of .52375/1 or .524/1, the best comparative measure may be the simple fraction of 11/21 that is suggested by the Grande Arche.

Image © Insecula.com

The sides of the Grande Arche are divided into 5 x 5 large panels and within each large panel are 7 x 7 smaller panels. Side lengths of 110 meters suggest lengths of 22 meters for the sides of the large panels with lengths of 22/7 meters for the sides of the smaller panels. The fraction 22/7 equals 3.1428, an accurate expression of π that is also found in the dimensions of the Great Pyramid. Side lengths of 210 cubits in the Grande Arche suggest lengths of 42 cubits for the sides of the large panels and 6 cubits for the sides of the smaller panels. This also shows that the relationship between the meter and the cubit is 6/π, using the measure of 22/7 for π:

21/11 = 6/π

22/7 x 21/11 = 6

The northern pyramid at Dashur, known as the Red Pyramid, was the first true (smooth sided) pyramid built in Egypt and it was the last pyramid built prior to construction of the Great Pyramid. The baselengths of the Red Pyramid are 420 cubits (220 meters) long, 20x multiples of 21/11.

Image by Jon Bodsworth

One of the oldest stone circles in England is at Rollright. The diameter of the Rollright circle is 31.4 meters, an accurate expression of π times 10 meters. Given the 6/π relationship between the meter and the cubit, the diameter of the Rollright circle is also 60 ancient Egyptian cubits.

BACK

http://home.hiwaay.net/~jalison/Art5.html

Resposta  Missatge 85 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 20/01/2025 15:28
illuminati+catholic+pyramid+eye+001.jpg (533x640 pixels)
Resultado de imagen para cydonia mars number 33

ANCIENT EGYPTIAN GEODESY - PART II

The great circle alignment from Giza to Alexandria has an azimuth of 51.85° north of due west from Giza (the same angle as the slope of the Great Pyramid). Extended beyond Alexandria, this great circle also crosses over Delphi, Rollright and Newgrange, as well as the city of London.

Map image © VectorGlobe

The azimuth of a great circle alignment from Dendera to Paris is also 51.85° north of due west.

Map image - Roger Hedin

Dendera was dedicated to Isis/Sirius. The ancient Egyptian year began on the date of the heliacal rising of Sirius in mid July. The helical rising of Sirius heralded the annual inundation of the Nile that was essential to the welfare of ancient Egypt. The axis of the temple of Isis at Dendera was aligned 20° south of due east, pointing directly at the rising point of Sirius from the latitude of Dendera.

Robert Bauval describes a number of connections between Isis/Sirius and Paris in Talisman (2004). Isis is shown riding on a boat in many ancient Egyptian drawings and carvings. At the direction of Napoleon, Sirius and a statue of Isis were added to the coat of arms for Paris shown below.

During the French revolution, a statue of Isis known as the Fountain of Regeneration was constructed on the former site of the Bastille. The engraving below commemorated this statue.

Fountain of Regeneration Engraving

The Elysian Fields is described as a place of eternal salvation in the ancient Egyptian Book of the Dead. Named after the Elysian Fields, the Champs Elysees is the main axis of Paris. The names Elysian and Elysees both suggest an association with Isis. The photograph below is facing southeast. The Arc de Triumphe is visible in the background. Beyond the Arc de Triumphe is the Louvre. The azimuth of the Champs Elysees is 26° south of due east, pointing directly at the rising point of Sirius/Isis from the latitude of Paris.

The termination point of the Champs Elysees to the northwest is the Grande Arche, in the foreground of the picture above. The axis of the Grande Arche is offset 6.33° south of the axis of the Champs Elysees. With an azimuth of just over 32° south of due east, the azimuth of the axis of the Grande Arche is the same as the azimuth of the great circle alignment from Paris to Dendera.

The Grande Arche is a nearly perfect cube with a height of 110 meters, a width of 108 meters and a depth of 112 meters. It is often described as a cube with side lengths of 110 meters. This is equal to 210 ancient Egyptian cubits:

110/210 = .5238

.5238 meters is a precise measure of the ancient Egyptian cubit, equating to 20.6222 inches, well within the ± .005 inches in Petrie's 20.62 inch measure of the ancient Egyptian cubit. Instead of the usual comparisons between the cubit and the meter of .52375/1 or .524/1, the best comparative measure may be the simple fraction of 11/21 that is suggested by the Grande Arche.

Image © Insecula.com

The sides of the Grande Arche are divided into 5 x 5 large panels and within each large panel are 7 x 7 smaller panels. Side lengths of 110 meters suggest lengths of 22 meters for the sides of the large panels with lengths of 22/7 meters for the sides of the smaller panels. The fraction 22/7 equals 3.1428, an accurate expression of π that is also found in the dimensions of the Great Pyramid. Side lengths of 210 cubits in the Grande Arche suggest lengths of 42 cubits for the sides of the large panels and 6 cubits for the sides of the smaller panels. This also shows that the relationship between the meter and the cubit is 6/π, using the measure of 22/7 for π:

21/11 = 6/π

22/7 x 21/11 = 6

The northern pyramid at Dashur, known as the Red Pyramid, was the first true (smooth sided) pyramid built in Egypt and it was the last pyramid built prior to construction of the Great Pyramid. The baselengths of the Red Pyramid are 420 cubits (220 meters) long, 20x multiples of 21/11.

Image by Jon Bodsworth

One of the oldest stone circles in England is at Rollright. The diameter of the Rollright circle is 31.4 meters, an accurate expression of π times 10 meters. Given the 6/π relationship between the meter and the cubit, the diameter of the Rollright circle is also 60 ancient Egyptian cubits.

BACK

http://home.hiwaay.net/~jalison/Art5.html

Resposta  Missatge 86 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 20/01/2025 16:13
No hay ninguna descripción de la foto disponible.
 
 
 
 
 
 
 

LUXOR . الأقــصــر

restSpodno68l75a1helic9ua3 0suuc47 h0p384.uudell0d 2h2m1elm   · 
 
'Sirius and Orion sailing across the sky at Dendera.'
Sirius and Orion are sailing across the firmament in boats on the astronomical ceiling in the outer hypostyle hall of the Hathor Temple at Dendera. The ceiling consists of seven separate strips but here we are looking at a detail of the upper register of the EASTERNMOST STRIP.
The star Sirius, or Sothis as it was known by the Egyptians, is depicted here as a reclining cow on a boat but the star was also identified with the goddess Isis. The rise of Sirius on the eastern horizon, after a few weeks of invisibility, signaled the beginning of the summer Nile flood for the Egyptians and the beginning of the New Year.
The second boat carries a god who personifies the constellation Orion, or Sahu as he was called by the Egyptians. The text above the god describes him as 'Sahu, the soul (ba) of Osiris' and thus it can be understood that Osiris is looking back at his wife Isis (in the shape of a cow) to see if she is following him across the sky. Orion/Osiris as a god looking back first appears in Egyptian iconography in stars clocks on coffin

Resposta  Missatge 87 de 87 del tema 
De: BARILOCHENSE6999 Enviat: 20/01/2025 16:33

African Astronomy: Kemetic knowledge of the stars

 
cornerston (45) en #africa • hace 7 años

I have discussed the advanced astronomical knowledge of the Dogon people of Mali. The Dogon believe that they came from Ancient Egypt, Kemet. In this piece, we are going to touch lightly on some of their knowledge of the constellations. I confess that I am not doing my ancestors any justice by such a very scanty piece.

The Ancient Egyptians (Kemites) 3,000 years ago were the first to record the variability of a distant star – and their records could provide useful information for astronomers today.

This star, the brightest star known to us as Sirius, the dog-star, has great meaning to our ancestors of Kemet (modern-day Egypt), and their descendants the Dogon tribe of Mali. The Kemites could predict the flooding of the Nile by observing the movement of Sirius, and such studies led them to develop the calendar which we use today.

Sirius-Star-System.jpg

The Kemites knew at least 43 constellations in the 13th century B.C. In 1100 B.C. Amenhope wrote the "Catalog of the Universe" in which he identified the major known constellations.

Aristotle astro1.png

The Kemites believed in a spherical earth revolving on its own axis while inferior planets like Mercury and Venus revolve around the Sun. They also knew about five planets, the retrograde motion of Mars was known, the revolution of Mercury and Venus around the Sun was known. This is what Macrobius Ambrosius Theodosius termed the “Egyptian system,” and went on to say that "it did not escape the skill of the Egyptians."

Flat earth theory.jpg

Ancient Egyptians were very interested in the night sky. They were drawn to two bright stars in the North Pole: "the indestructibles" or what we called today as Kochab, in the bowl of the Little Dipper (Ursa Minor), and Mizar, in the middle of the handle of the Big Dipper (Ursa Major).

Kochab and Mizar.jpg

One great evidence of their mastery of the constellations and how their belief in the afterlife can be best illustrated in the sophisticated, decorative illustrations on the roof of the tombs of Rameses VI and Rameses IX in the valley of the Kings in present-day Luxor.

Astro ceiling in tomb of Ramases IV-Part1.jpg

Astro inscription in ceiling on tomb of Ramases IV in Luxor.jpg

Ramses IV astro ceiling.jpg

Ramases IV tomb-walls and ceiling astro.jpg

Kemetic astronomy, astrology and religious rites were intermingled. The periods and durations of religious rituals were systematically determined by studying and recording the movements of heavenly bodies, the sun, moon, constellations and stars. These can be evidenced from records found in temples. They built their pyramids and other major structures in alignment with constellations. This we will explore in the next piece.

astro9.gif

https://steemit.com/africa/@cornerston/african-astronomy-kemetic-knowledge-of-the-stars


Primer  Anterior  73 a 87 de 87  Següent   Darrer  
Tema anterior  Tema següent
 
©2025 - Gabitos - Tots els drets reservats