|
|
General: ERATOSTENES= ALEJANDRIA (SEDE COPTA-JUAN MARCOS)=TIERRA REDONDA=ROSE LINE
Elegir otro panel de mensajes |
|
|
Eratóstenes
Eratóstenes de Cirene (en griego antiguo Ἐρατοσθένης, Eratosthénēs) (Cirene, 276 a. C.1-Alejandría, 194 a. C.) fue un matemático, astrónomo y geógrafo griego de origen cirenaico.
Eratóstenes era hijo de Aglaos. Estudió en Alejandría y durante algún tiempo en Atenas. Fue discípulo de Aristón de Quíos, de Lisanias de Cirene y del poeta Calímaco y también gran amigo de Arquímedes. En el año 236 a. C., Ptolomeo III le llamó para que se hiciera cargo de la Biblioteca de Alejandría, puesto que ocupó hasta el fin de sus días. La Suda afirma que, tras perder la vista, se dejó morir de hambre a la edad de 80 años; sin embargo, Luciano dice que llegó a la edad de 82 años; también Censorinosostiene que falleció cuando tenía 82 años.
Esfera armilar[editar]
A Eratóstenes se le atribuye la invención, hacia 255 a. C., de la esfera armilar que aún se empleaba en el siglo XVII. Aunque debió de usar este instrumento para diversas observaciones astronómicas, sólo queda constancia de la que le condujo a la determinación de la oblicuidad de la eclíptica. Determinó que el intervalo entre los trópicos (el doble de la oblicuidad de la eclíptica) equivalía a los 11/83 de la circunferencia terrestre completa, resultando para dicha oblicuidad 23º 51' 19", cifra que posteriormente adoptaría el astrónomo Claudio Ptolomeo.
Según algunos historiadores, Eratóstenes obtuvo un valor de 24º y el refinamiento del resultado se debió hasta 11/83 al propio Ptolomeo. Además, según Plutarco, de sus observaciones astronómicas durante los eclipses dedujo que la distancia al Sol era de 804 000 000 estadios, la distancia a la Luna 780 000 estadios y, según Macrobio, que el diámetro del Sol era 27 veces mayor que el de la Tierra. Realmente el diámetro del Sol es 109 veces el de la Tierra y la distancia a la Luna es casi tres veces la calculada por Eratóstenes, pero el cálculo de la distancia al Sol, admitiendo que el estadio empleado fuera de 185 metros, fue de 148 752 060 km, muy similar a la unidad astronómica actual. A pesar de que se le atribuye frecuentemente la obra Katasterismoi, que contiene la nomenclatura de 44 constelaciones y 675 estrellas, los críticos niegan que fuera escrita por él, por lo que se suele designar Pseudo-Eratóstenes a su autor.
Medición de las dimensiones de la Tierra[editar]

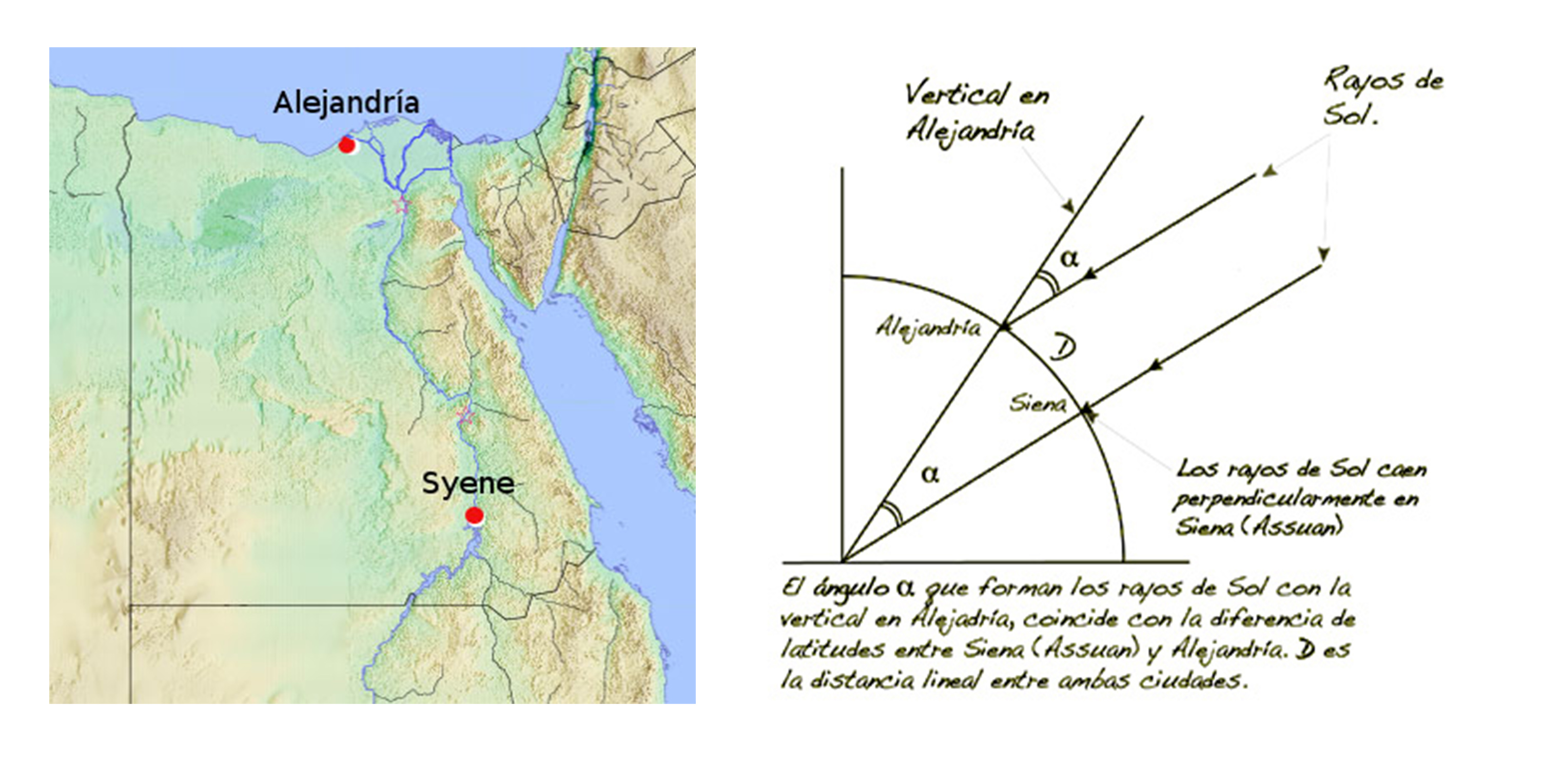
En el solsticio de verano, los rayos solares inciden perpendicularmente sobre Siena ( Asuán). En Alejandría, más al norte, midiendo la altura de un edificio y la longitud de la sombra que proyecta, se puede determinar el ángulo formado con el plano de la eclíptica, en el que se encuentran el Sol y la ciudad de Siena, ángulo que es precisamente la diferencia de latitud entre ambas ciudades. Conocida ésta, basta medir el arco de circunferencia y extrapolar el resultado a la circunferencia completa (360º).

Reconstrucción del siglo XIX (según Bunbury) del mapa de Eratóstenes del mundo conocido en su época.
Sin embargo, el principal motivo de su celebridad es sin duda la determinación del tamaño de la Tierra. Para ello inventó y empleó un método trigonométrico, además de las nociones de latitud y longitud, al parecer ya introducidas por Dicearco, por lo que bien merece el título de padre de la geodesia.
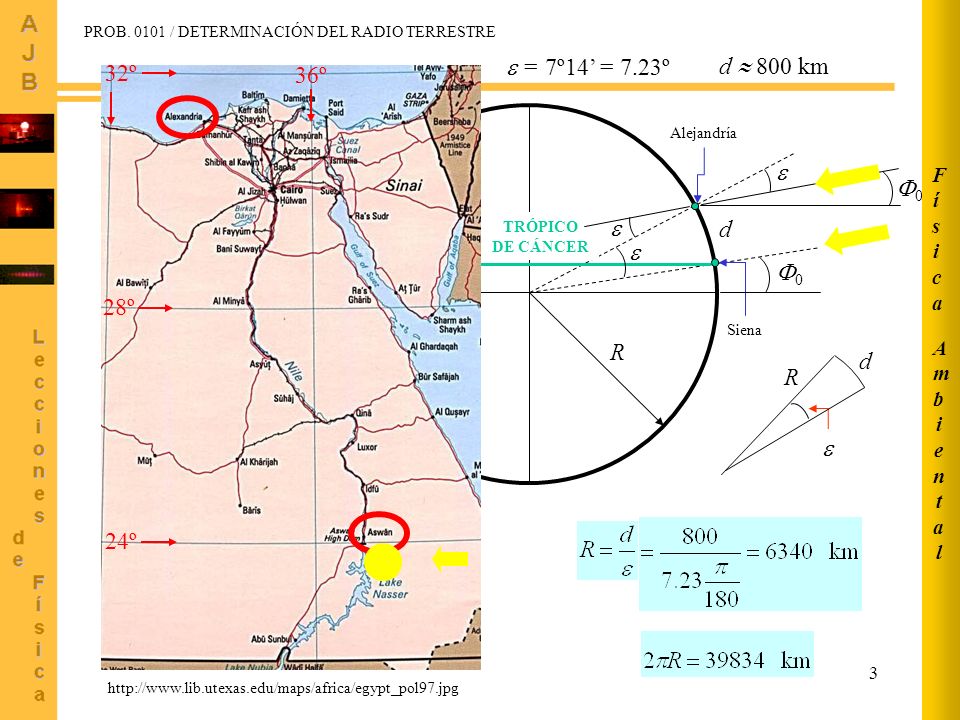
Por referencias obtenidas de un papiro de su biblioteca, sabía que en Siena (hoy Asuán, Egipto) el día del solsticio de verano los objetos verticales no proyectaban sombra alguna y la luz alumbraba el fondo de los pozos; esto significaba que la ciudad estaba situada justamente sobre la línea del trópico y su latitud era igual a la de la eclíptica que ya conocía. Eratóstenes, suponiendo que Siena y Alejandría tenían la misma longitud (realmente distan 3º) y que el Sol se encontraba tan alejado de la Tierra que sus rayos podían suponerse paralelos, midió la sombra en Alejandría el mismo día del solsticio de verano al mediodía, demostrando que el cenit de la ciudad distaba 1/50 parte de la circunferencia, es decir, 7º 12' del de Alejandría. Según Cleomedes, Eratóstenes se sirvió del scaphium o gnomon (un protocuadrante solar) para el cálculo de dicha cantidad.
Posteriormente, tomó la distancia estimada por las caravanas que comerciaban entre ambas ciudades, aunque bien pudo obtener el dato en la propia Biblioteca de Alejandría, fijándola en 5000 estadios, de donde dedujo que la circunferencia de la Tierra era de 250 000 estadios, resultado que posteriormente elevó hasta 252 000 estadios, de modo que a cada grado correspondieran 700 estadios. También se afirma que Eratóstenes, para calcular la distancia entre las dos ciudades, se valió de un regimiento de soldados que diera pasos de tamaño uniforme y los contara.
Admitiendo que Eratóstenes usase el estadio ático-italiano de 184.8 m, que era el que solía utilizarse por los griegos de Alejandría en aquella época, el error cometido sería de 6.192 kilómetros (un 15 %). Sin embargo, hay quien defiende que empleó el estadio egipcio (300 codos de 52,4 cm), en cuyo caso la circunferencia polar calculada hubiera sido de 39614 km, frente a los 40008 km considerados en la actualidad, es decir, un error de menos del 1%.
Ahora bien, es imposible que Eratóstenes diera con la medida exacta de la circunferencia de la Tierra debido a errores en los supuestos que calculó. Tuvo que haber tenido un margen de error considerable y por lo tanto no pudo haber usado el estadio egipcio:2
- Supuso que la Tierra es perfectamente esférica, lo que no es cierto. Un grado de latitud no representa exactamente la misma distancia en todas las latitudes, sino que varía ligeramente de 110,57 km en el Ecuador hasta 111,7 km en los Polos. Por eso no podemos suponer que 7º entre Alejandría y Siena representen la misma distancia que 7º en cualquier otro lugar a lo largo de todo el meridiano.
- Supuso que Siena y Alejandría se encontraban situadas sobre un mismo meridiano, lo cual no es así, ya que hay una diferencia de 3 grados de longitud entre ambas ciudades.
- La distancia real entre Alejandría y Siena (hoy Asuán) no es de 924 km (5000 estadios ático-italiano de 184,8 m por estadio), sino de 843 km (distancia aérea y entre los centros de las dos ciudades), lo que representa una diferencia de 81 km.
- Realmente Siena no está ubicada exactamente sobre el paralelo del trópico de cáncer (los puntos donde los rayos del sol caen verticalmente a la tierra en el solsticio de verano). Actualmente se encuentra situada a 72 km (desde el centro de la ciudad). Pero debido a que las variaciones del eje de la Tierra fluctúan entre 22,1 y 24,5º en un período de 41000 años, hace 2000 años se encontraba a 41 km.
- La medida de la sombra que se proyectó sobre la vara de Eratóstenes hace 2.200 años debió ser de 7,5º o 1/48 parte de una circunferencia y no 7,2º o 1/50 parte. Puesto que en aquella época no existía el cálculo trigonométrico, para calcular el ángulo de la sombra, Eratóstenes pudo haberse valido de un compás,3 para medir directamente dicho ángulo, lo que no permite una medida tan precisa.
https://es.wikipedia.org/wiki/Erat%C3%B3stenes
|
|
|
|
|
LA MEDIDA DEL PIE TIENE ORIGEN MATEMATICO, APARTE DE LOS PIES DEL SER HUMANO, TAMBIEN EN EL MERIDIANO DE LA TIERRA-RELACION CON ROSE-LINE-UNGIMIENTO DE MARIA MAGDALENA DE LOS PIES DE CRISTO EN BETANIA.

Pie (unidad)
De Wikipedia, la enciclopedia libre
El pie es una unidad de longitud de origen natural, basada en el pie humano, ya utilizada por las civilizaciones antiguas.
El pie romano, o pes, equivalía, como media, a 29,57 cm; el "pie carolingio", o anteriormente denominado «pie drusiano o drúsico» [pes drusianus], equivalía a nueve octavos del romano, esto es, aproximadamente 33,27 cm; y el pie castellano equivalía a 27,8635 cm.[1]
Actualmente, el pie ha sido sustituido en casi todo el mundo por las unidades del Sistema Internacional (SI), salvo en el uso corriente en algunos países anglosajones, donde equivale a 30,48 centímetros. Es también la unidad de medida empleada en aeronáutica para hacer referencia a la altitud.
La primera referencia histórica referida a una medida estándar del «pie» se relaciona con la civilización sumeria, gracias a una definición de la medida encontrada en una estatua de Gudea de Lagash. Según la creencia más popular, se originó tras un descanso en una extenuante jornada de trabajo. El encargado de medir los bloques de piedra no era capaz de incorporarse y decidió que sería mucho más cómodo, para medir los bloques desde el suelo, utilizar los pies desde su posición.[cita requerida]
Sin embargo, los arqueólogos piensan que los egipcios y mesopotámicos favorecieron el codo, mientras que los romanos y los griegos prefirieron el pie. Originalmente tanto los griegos como los romanos dividieron el pie en 16 dígitos o dedos, pero en los últimos años, los romanos también lo dividieron en 12 unciae (de donde derivan las palabras inglesas inch, "pulgada" y ounce, "onza"). El pie griego (ποὐς, pous) variaba de una ciudad a otra, oscilando entre 270 y 350 mm, pero las longitudes utilizadas para la construcción de templos parecen haber sido alrededor de 295 o 325 mm, siendo el primero cercano al tamaño del pie romano. El pie dórico, utilizado en el orden dóricooscilaba entre 325 y 328 mm. El pie romano estándar (pes) era normalmente de 295,7 mm, pero en las provincias, se utilizaba el pes Drusianus (pie de Nerón Claudio Druso) con una longitud de aproximadamente 334 mm. (En realidad, este pie está constatado anteriormente a Druso).[2]
Después de la caída del Imperio Romano, se continuó con algunas medidas tradicionales romanas, pero otras cayeron en desuso. En el año 790, Carlomagno intentó reformar las unidades de medida en sus dominios. Sus unidades de longitud se basaron en la toise y, en particular, la toise de l'Ecritoire, la distancia entre las puntas de los dedos de los brazos extendidos de un hombre.[3] La toise tiene 6 pied (pie) de 326.6 mm.
Sin embargo, no tuvo éxito en la introducción de una unidad estándar de longitud en todo su reino. Durante el siglo IX se utilizó un pie romano de 296,1 mm, y en el siglo X, un pie de unos 320 mm. Al mismo tiempo, los edificios monásticos utilizaban el pie carolingio de 340 mm.[4]
Nomenclatura en inglés
- 1 foot (singular)
- 3 feet (plural)
- 3 ft (abreviado)
- 3 ’ (comilla simple)
Equivalencias
Actualmente el pie se utiliza sólo como unidad de medida popular en los países anglosajones de Estados Unidos, Canadá y Reino Unido, y todavía se emplea en aeronáutica (incluso fuera de los países anglosajones) para expresar la altitud de aviones y otros vehículos aéreos. La adopción por estos países del Sistema Internacional (SI) hace ya unos años irá haciendo caer en desuso esta unidad, incluso en estos países.
Era usual utilizarlo para longitudes de hasta unos tres metros; para longitudes mayores se suele emplear la yarda o la milla. La excepción es la altitud de los aviones, que aún hoy se sigue expresando en miles de pies en casi todos los países.
Para el acotamiento de tierras y costas, el Sistema Público de Agrimensura de Tierras (de Estados Unidos) utiliza una variedad llamada «pie de agrimensura», cuya longitud equivale a 30,4800609601219 centímetros.
En la industria de la madera es usual utilizar el «pie maderero», tratándose en este caso de una unidad de volumen. Su valor es el que corresponde a una pieza cuadrada de 1 pie de lado y 1 pulgada de espesor. 1 pie maderero es igual a 2.359,737216 (un pie maderero entra 423.7 veces en un metro cubico);cm3 (30,48 cm * 30,48 cm * 2,54 cm).
El Padre Lamy en su Apparatus[5] (1696) describe el "pie de burgos" como una longitud de 1 8.5/11 codos antiguos romanos.
Superficie cuadrada de un pie castellano de lado, equivalente a 0,077637 m².
Efectivamente se calcula que la longitud total del meridiano es de 40008 kilometros aproximadamente. Teniendo en cuenta que en el mismo tenemos 360 grados de 60 minutos, que a la vez tambien tienen 60 segundos, tenemos que en los 360 grados equivalen a 129600000 segundos.
360 * 60 * 60 = 1296000
40 008 * 100 000
Observamos que 40008 kilometros equivalen a 4000800000 centimetros. Si dividimos para saber cual es la equivalencia en segundo sexagesimal en centimetros, insisto, del MERIDIANO TERRESTRE TENEMOS QUE HACER LA SIGUIENTE ECUACION
4000800000/1296000=
4 000 800 000 / 1296 000= 3087.03703704
EFECTIVAMENTE 100 PIES APROXIMADAMENTE EQUIVALEN A UN SEGUNDO SEXAGESIMAL DEL MERIDIANO TERRESTRE. EL PIE GRIEGO ERA MUY APROXIMADO A 30.8 CM.
|
|
|
|
|
| |
|
|
©2025 - Gabitos - Todos los derechos reservados | |
|
|

