podemos ver la imagen de un hipercubo en movimiento

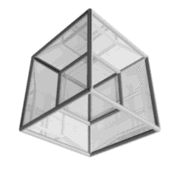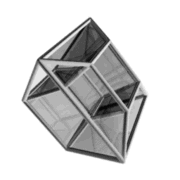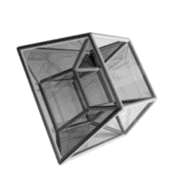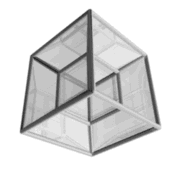
Este cubo tiene la peculiaridad de ser en 4-D, por lo que es normal que no lo veais del todo claro a primera vista.

Pues no tiene tanto misterio…

Sí, puede parecer que sólo es un cubo que va moviéndose, pero tendreis que tener en cuenta que:

- Todos los ángulos de la estructura son rectos.

- Entre el cubo exterior e interior, hay más cubos, estos en 3-D, y siempre sin perder sus ángulos rectos y su forma cúbica.

- Un hipercubo contiene 16 vértices, 32 aristas, 24 caras y 8 celdas cúbicas.

Y ya si queremos ‘entenderlo’ del todo, nada mejor que la siguiente definición:

“Un hipercubo se define como un cubo desfasado en el tiempo, es decir, cada instante de tiempo por el cual se movió pero todos ellos juntos. Por supuesto no podemos ver un hipercubo en la tercera dimensión, ya que solo se verían los puntos que tocan nuestro universo, así que solo veríamos un cubo común.

No podemos ver un hipercubo porque estamos “encerrados” en tres dimensiones, por lo que solo podemos ver la sombra de lo que seria un hipercubo. Se parece a dos cubos anidados, con todos los vértices conectados por líneas. Pero en el teseracto real de cuatro dimensiones todas las líneas tendrían la misma longitud y todos los ángulos serían ángulos rectos.”

Me encanta.

Pero vamos a intentar hacerlo más sencillo. ‘Intentar’ es la palabra.

Entendamos el hipercubo

Sobre 1990, el matemático inglés Charles Howard Hinton se propuso hacer entender a la gente la posibilidad del hipercubo.

Su teoría era la siguiente: imagina que conoces a un par de amigos que son en 2-D, y les tienes que explicar qué es un cubo 3-D. Ellos no te entenderían ya que sólo serían capaces de ver una de sus caras.

A no ser que descompusiéramos el cubo en sus 6 caras, claro.

Pues si un ser de 4-D tuviera que explicarnos qué es un hipercubo, tendría que enseñarnos su descomposición en cubos 3-D, para que fuéramos capaces de entenderlo.

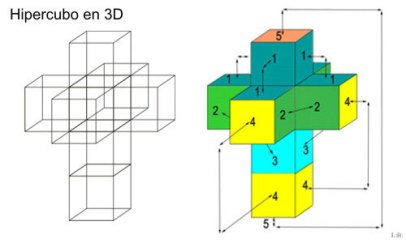
¿A que ahora parece más sencillo? Pues no sé si deciros que, para formar el hipercubo, abría que unir todas las caras con el mismo número (es decir, las caras 1 con las 1, las 2 con las 2…).

No intenteis imaginar físicamente esa unión, recordad que somos limitadillos en esto del 4-D.

Pero bueno, veamos un poco de arte, para relajarnos y olvidar tanta complejidad de hipercubos. Os pongo un cuadro cualquiera, por ejemplo, uno de Dalí que he encontrado en una página sobre arte: