|
|
| De: Thenard (Mensaje original) |
Enviado: 17/06/2010 22:08 |
NUEVA COMPRENSIÓN DEL SISTEMA SOLAR
|
A partir por lo menos de la época de Ptolemaica en el 2do ANUNCIO del siglo, el hombre creyó que la tierra estaba en el centro del universo. En el décimo quinto siglo, Copernico nos trajo más cerca la verdad, moviendo el sol al centro del universo.
Galileo, Kepler y otros ayudaron a movernos desde nuestra opinión geocéntrica del universo, pero en el final del vigésimo siglo, la ciencia todavía expresa las relaciones planetarias de la Sistema Solar usando la "unidad astronómica," la distancia de la tierra del sol.
|
|
|
¿Con excepción del hecho de que habitamos la tierra, hay razón lógica de basar estas relaciones en el tercer planeta del sistema? ¿Somos geocéntricos ol revés, en nuestro pensamiento?
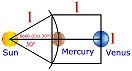
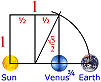
Heche una ojeada nuevo la Sistema Solar y vea las relaciones increíbles que resultan cuando el mercurio, el primer planeta, se utiliza como medida patron para otros planetas.
|
|
El Sistema Solar: ¿casualidad o diseño?
|
¿Es nuestro Sistema Solar el producto de la casualidad o del diseño divino? ¿En nuestra opinión al centrar la Tierra en el Sistema Solar ha enmascarado las relaciones matemáticas únicas que existen entre los planetas? Si, en vez de la tierra, utilizasemos a mercurio, el primer planeta, como la base para medir distancias y períodos planetarios de la órbita alrededor del sol, consiguiriamos estas relaciones:
| Planeta |
Distancia
de
el sol
en el kilómetro (000) |
Distancia
donde
Mercurio
iguales 1 |
Período
donde
Mercurio
iguales 1 |
| Mercurio |
57,910 |
1,0000 |
1,0000 |
| Venus |
108,200 |
1,8660 |
2,5490 |
| Tierra |
149,600 |
2,5833 |
4,1521 |
| Marte |
227,940 |
3,9365 |
7,8101 |
| Júpiter |
778,330 |
13,4399 |
49,2714 |
|
Cuando se revela mercurio = 1, las relaciones
|
Curiosamente, estas medidas revelan algunas relaciones muy inusuales entre los planetas, que se ocultaban al usar la tierra como la unidad de la medida básica:
(Tierra 4 /Venus 3) + (Venus 3 /Tierra 4) = 7
(Marte 4 /Tierra 3) + (Tierra 3 /Marte 4) = 14
¾ De la Tierra * ( Ö 1 + Ö 2 + Ö 3 + Ö 6) = Júpiter
|
Las relaciones existen en períodos orbitales también
|
 Las relaciones entre los planetas también se extienden a los períodos de la rotación orbital , como los funcionamientos de un reloj exacto calibrado:
Distancia de la tierra = período de Ö de Venus * Phi
Distancia de Marte = período de Ö de la tierra * diámetro de Ö de la órbita de Venus
Nota: Phi es igual a 1,6180339..., el número detrás de la sección de oro o la proporción divina, encontró en cada proporción del cuerpo humano.
|
Las geometrias elegantes relacionan los planetas
|
Encontramos también que las distancias y los períodos de los planetas se pueden representar por fundamentos que solo aparecen en las construcciones geométricas armoniosas de círculos, triángulos y los cuadrados:
Observese también que los ángulos en estas geometrias utilizan las divisiones más fundamentales de un círculo en 4, 6 y 12 secciones (es decir, secciones de 90º , 60º y 30º ), y los números más fundamentales del número entero de su construcción.
|
Incluso la luna revela una relación altamente inusual
|
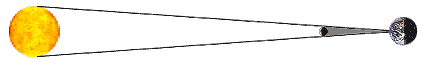
Los eclipses solares totales son posibles solamente debido a una relación única entre el sol y la luna, que es 400 veces más cercano a la tierra que el sol, pero también 400 veces más pequeño que el sol.
¿Los leyes de Kepler del movimiento planetario nos dicen que que la distancia de cada planeta esté relacionada con su propio período orbital, pero que hay una razón natural para que una órbita del planeta sea relacionada con otra?
¿Habrían podido todas estas relaciones suceder por mera coincidencia o es producto de la mente de divina el diseño de la Sistema Solar?
|
Las distancias de los planetas al sol,
tradicionalmente y con geometría solar
| ¡Medir el Sistema Solar por la tierra es incorrecto! |
En todas las cartas tradicionales, las distancias del Sistema Solar se basan en la medida de la distancia de la tierra al sol, conocida como una unidad astronómica. Las distancias de los planetas se demuestran así como sigue:
| Planeta |
Distancia
del sol
en km (000)
por la NASA |
Distancia
en AU
por la NASA |
| Mercurio |
57,910 |
0,3871 |
| Venus |
108,200 |
0,7233 |
| Tierra |
149,600 |
1,0000 |
|
Marte
|
227,940 |
1,5237 |
| Júpiter |
778,330 |
5,2034 |
(nota: La NASA usa comas, pero los resultados calculados son solamente exactos al número de decimales en los valores usados, que en este caso es la distancia en kilómetros.)
| El mercurio se debe utilizar como la unidad de medida |
Si basamos las medidas del Sistema Solar en la distancia de mercurio al sol, se consiguen estas medidas:
| Planeta |
Distancia
del sol
en el km (000) |
Distancia
donde
Mercurio
igual a 1 |
| Mercurio |
57,910 |
1,0000 |
| Venus |
108,200 |
1,8684 |
| Tierra |
149,600 |
2,5833 |
| Marte |
227,940 |
3,9361 |
| Júpiter |
778,330 |
13,4403 |
| Entonces conservemos solamente las relaciones planetarias vistas |
Es un cambio simple, pero esta nueva visión revela una penetración increíble en las relaciones entre los planetas. Cada una de estas medidas de la distancia se puede representar con un patrón armonico de números enteros simples a partir de 1 a 6, que aparecen en raíces, multiplicadores y exponentes:
| Mercurio = 1 = ½ ( Ö 1+1) |
| Mercurio en el aphelion = ½ ( Ö 2 + 1) |
| Venus = Mercurio * ² (Del ½ ( Ö 3 + 1) ) |
| ¾ De la Tierra = De Venus * (½ ( Ö 5 + 1)) |
| ¾ De Marte = De la Tierra * (½ ( Ö 6 + Ö 2)) |
| Júpiter = Marte * ( Ö 2 + 2) |
Nota: Ö x indica la raíz cuadrada de x
| La acumulación demuestra la distancia de cada uno al sol |
La distancia de cada planeta del sol, usando el mercurio como 1, se puede representar así como acumulación de estas relaciones. Una representación alterna del mismo número se utiliza para Venus para conectar a tierra para agregar la penetración al patrón interesante que se convierte:
| Mercurio = ½ ( Ö 1+1) |
| Venus = (½ ( Ö 3+1)) ² |
| Tierra = ((½ ( Ö 3+1))^(½( Ö 4+1))*(½( Ö 5+1))) |
| Marte = ((½ ( Ö 3+1))^(½( Ö 4+1))*(½( Ö 5+1)))^¾*(½( Ö 6+ Ö 2)) |
| =(((½(Ö 3+1))^(½( Ö 4+1))*(½( Ö 5+1)))^¾*(½( Ö 6+ Ö 2)))*( Ö 2+2 de Júpiter) |
| Los resultados son asombrosamente exactos |
Las distancias calculadas por estas fórmulas son casi idénticas a las distancias relativas publicadas por NASA :
| Planeta |
Publicado
distancia
del sol en km
(000) |
Distancia relativa
del sol,
donde
Mercurio=1 |
Alan
Bennett
calculado
valor por
sobre |
Grado
de
Variación |
| Mercurio |
57,910 |
1,0000 |
1,0000 |
0,0000 |
| Venus |
108,200 |
1,8684 |
1,8660 |
0,0013 |
| Tierra |
149,600 |
2,5833 |
2,5833 |
0,0000 |
| Marte |
227,940 |
3,9361 |
3,9365 |
-0,0001 |
| Júpiter |
778,330 |
13,4403 |
13,4399 |
0,0000 |
| Pero esto es justo el principio de las relaciones increíbles existentes. |
|
| De: |
Enviado: 03/07/2005 18:41 |
El Geometries Solar
Las distancias de cada planeta al sol, se pueden describir por una representación geométrica única, o geometría solar, para cada par de planetas, según lo demostrado abajo.
Nota: Ö x indica la raíz cuadrada de x.
Mercurio = 1
Perihelio = ½ 2 ( Ö 2+1) = 0,792893
Afelio = ½ ( Ö 2+1) = 1,207107
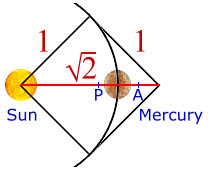
Comience con un círculo para la distancia orbital corta de mercurio, y después construya un cuadrado con los lados de la misma longitud. El punto mediano entre el radio del círculo y de la diagonal del cuadrado es el afelio del mercurio (a), el punto exterior de su órbita. La misma distancia hacia el sol es el perihelio de mercurio (p), el punto interior de su órbita.
Venus = Mercurio * ² (Del ½ ( Ö 3 + 1) ) = 1,866025
Venus = 1,000000 * 1,866025 = 1,866025
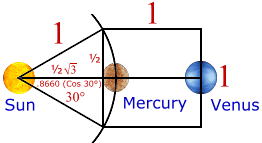
Comience con un círculo para la distancia orbital mala del mercurio, divida el círculo en seis secciones iguales, dibuje una línea para formar el triángulo equilátero de una sección y después para dibujar un cuadrado usando líneas de la misma longitud para conseguir la distancia orbital de Venus.
¾ De la Tierra = De Venus * ½ ( Ö 5 + 1) = 2,583306
Tierra = 1,596571 * 1,618034 = 2,583306
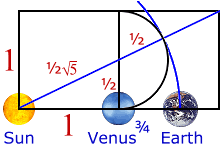
Comience con la energía del ¾ de la distancia orbital de Venus, y después construya la "sección de oro" o tambien llamada la "proporción divina" para conseguir a la distancia orbital de la tierra.
¾ De Marte = De la Tierra * ½ ( Ö 6 + Ö 2) = 3,936458
Marte = 2,037661 * 1,931852 = 3,936458
Nota: ½ ( Ö 6 + Ö 2) = 2 * coseno 15º = 1,931852
También: Ö (2 * Venus) = Ö (diámetro de Venus) = 1,931852
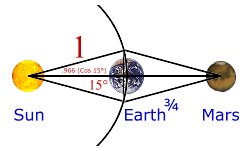
Comience con un círculo usando la energía del ¾ de la distancia orbital de la tierra como su radio, divida el círculo en doce secciones iguales, dibuje una línea para formar el triángulo isósceles de la sección y después para dibujar otro triángulo isósceles en el otro lado usando las líneas de la misma longitud, formando un diamante, para conseguir la distancia orbital de Marte.
|
|
|
|
|
Primer
Anterior
2 a 2 de 2
Siguiente
Último
|
|
|
|
De: Thenard |
Enviado: 17/06/2010 22:08 |
Júpiter = Marte * ( Ö 2 + 2) = 13,439908
Júpiter = 3,936458 * 3,414214 = 13,439908
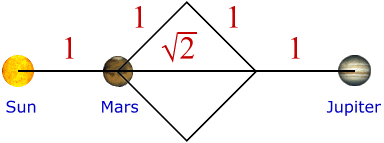
Comience con la distancia orbital de Marte, agregue un cuadrado hecho con la distancia orbital de Marte dada vuelta en una diagonal y después agregue la distancia orbital de Marte otra vez para conseguir la distancia orbital de Júpiter.
Los geometrias que resultan son hermosas y elegantes y del todo simples. Puede que estos patrones intrigantes suceden por coincidencia. . . ¿o por diseño? Antes de decidir, hechemos una ojeada a cómo la tierra se relaciona con los otros planetas.
Tierra y la relación a Phi
Según lo demostrado en la página del cálculo de la distancia, la distancia de la tierra del sol, donde 1 es mercurio, se computa como sigue:
((½ ( Ö 3 + 1)) ^ (½ ( Ö 4 + 1))) * (½ ( Ö 5 + 1))
Nota: Ö x indica la raíz cuadrada de x
Hay algo absolutamente increíble sobre esta derivación para la tierra.
|
Observe el ½ de repetición del término ( Ö x + 1) con 3, 4, y 5
|
| Primero, es absolutamente asombroso que la misma forma de:
½ ( Ö x + 1)
aparecería en tres términos sucesivos usando los números enteros 3, 4, y 5 para x.
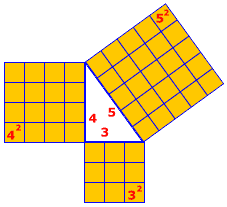
están, por supuesto, los números enteros 3, 4 y 5 dominantes usados en el ejemplo más elemental de la teoría de Pythagorean para los triángulos derechos, donde
3 2 + 4 2 = 5 2 .
|
 |
|
El tercer término, ½ ( Ö ¡5 + 1), es Phi!
|
 |
Más increíble con todo es que el tercer término, ½ ( Ö 5 + 1), no es ninguno con excepción del número ubicuo 1,6180339..., mejora conocido como phi, o ¦. Phi tiene características matemáticas de semejante de cualquier otro número. El recíproco de ¦ es ¦-1, o 0,6180339... . Cuando una línea se divide en 1/¦, el cociente de la sección pequeña a la sección grande será idéntico al cociente de la sección grande a la línea entera.
|
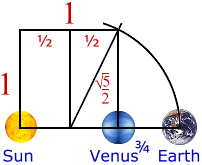
Esto da lugar a la relación increíble de 1 y ¦ entre Venus ( a la energía del ¾) y la tierra:
|
¡Phi aparece en el diseño de muchas formas de la vida!
|
|
Phi es el número detrás de la sección de oro, o proporción divina, y la serie de fibonacci. Aparece en todas partes en organismos vivos en todo de cada dimensión dominante del cuerpo humano, a los espirales de las cáscaras del mar, a los arreglos de vástagos en una planta.
|
 |
|
Semejanzas en la derivación de Phi y de la distancia de la tierra.
|
También es interesante que la derivación de Phi es tan similar a la derivación de la distancia de la tierra del sol. Considere la semejanza en la construcción formulada, en donde los primeros dos términos utilizan un exponente y entonces un multiplicador.
Phi se deriva de:
¦ de = 5 5 ^ * 5 + 5 = 1,6180339...
Mientras que la distancia de la tierra del sol, donde está mercurio = 1:
½ del ½ ( Ö 3 + 1) ^ ( Ö 4 + 1) * ½ ( Ö 5 + 1) = 2,583306...
|
La tierra incorpora los dos tesoros de la geometría
|
Es como si la tierra incorpora la teoría de Pythagoras y la sección de oro a una construcción hermosa.
 |
Quizás Johannes Kepler (matemático y el astrónomo, 1571-1630) tenía mayor penetración en el universo que nosotros pudo haber sospechado cuando él dijo:
|
| la "geometría tiene dos grandes tesoros: uno el teorema de Pythagoras; la otra, la división de una línea en cociente extremo y malo. El primer podemos comparar a una medida de oro; el segundo podemos nombrar una joya preciosa." |
http://solargeometry.com/
|
|
|
|
|
Tema anterior
