El Numero PHI - El Ojo de la Luz

¿Qué es phi?

Phi (1.618033988749895... ), pronunciado como fi, es un numero irracional como Pi ( 3.14159265358979... ), pero con muchas características matemáticas inusuales. Phi es la base de la Proporción Dorada. La razón o proporción determinada por Phi (1.618...) era conocida por los Griegos como la “Sección Dorada” y por los artistas del renacimiento como la “Proporción Divina”. También se le conoce como la razón Dorada o la Proporción Áurea.
Phi, como Pi, es una razón definida por una construcción geométrica.
Pi es la relación de la circunferencia de un círculo respecto a su diámetro. Phi es la proporción de los segmentos de una línea que resultan cuando una línea es dividida de una forma única y especial.

La línea es dividida para que la proporción de la longitud de la línea entera (A) respecto a la longitud del segmento de la línea mayor (B) sea igual que la proporción de la longitud del segmento de la línea mayor (B) a la longitud del segmento de la línea menor (C)

Esto es que A es 1.618... veces B, y B es 1.618… veces C. Recíprocamente, C es 0.618... de B y B es 0.618... de A. Phi con mayúscula "Phi" es 1.6180339887..., mientras que phi con minúscula es 0.6180339887, el reciproco de Phi o Phi menos 1.

Lo que hace a phi incluso mas inusual es que puede derivarse de muchas formas y ser encontrado en proporcionalmente en el universo. Phi F puede ser derivado por: la serie numérica descubierta por Leonardo Fibonacci, matemáticas y geometría.

Phi y la serie de Fibonacci

Leonardo Fibonacci, por herencia del mundo árabe, descubrió la serie que nos lleva a phi. En el siglo XII, Leonardo Fibonacci descubrió una serie numérica simple que es la base de la increíble relación que encontramos detrás de phi. Empezando con 0 y 1, cada número de la serie es simplemente la suma de los dos anteriores. Así: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .

La razón (proporción) de cada par sucesivo de números en la serie se aproxima a phi (1.618. . .). Así si dividimos 5 entre 3 es 1.666..., y 8 entre 5 es 1.60. En la medida en la que vamos mas lejos del 0 (punto de inicio de la secuencia) nos acercamos al valor de phi.

La tabla de abajo nos muestra como las proporciones de números sucesivos en la serie Fibonacci se aproxima a Phi.

Puedes computar cualquier número de la serie Fibonacci fácilmente. Usa phi para saber cualquier numero (n) de la serie Fibonacci (f)

fn = Fn / 5½

Phi puede derivarse matemáticamente resolviendo la ecuación:
n2 - n1 - n0 = 0 que es lo mismo que n2 - n - 1 = 0
Esta ecuación la rescribimos y nos queda así:
n2 = n + 1 y 1 / n = n - 1
La solución a la ecuación es la raíz cuadrada de 5 más 1 dividido entre 2
( 5½ + 1 ) / 2 = 1.6180339... = F

Esto resulta en dos propiedades únicas de phi:
Si elevas al cuadrado a phi, obtienes un numero exactamente 1 mayor que phi: 2.6180...
F2 = F + 1
Si divides a phi entre 1, obtienes un numero exactamente a 1 menos phi: 0.6180...:
1 / F = F - 1

Phi, curiosamente, puede ser expresado en cinco: 5 ^ .5 * .5 + .5 = F

Puedes usar phi para computar un número n en la serie Fibonacci (fn): fn = Fn / 5½

Como por ejemplo, el número 40 de la serie Fibonacci es 102, 334, 155, que puede expresarse
f40 = F40 / 5½ = 102,334,155

Este método en realidad nos provee un estimado que siempre esta cerca del numero correcto Fibonacci.

Funciones trigonométricas

También Phi puede ser relacionada a Pi por funciones trigonométricas.

Phi puede ser relacionado con “e”, base de los logaritmos naturales, por el inverso hiperbólico de la función seno: F = e ^ asinh(.5)

Puede ser expresado como un límite, dándonos una idea de su capacidad de auto recurrencia:

Es importante mencionar que phi es tanto una razón aritmética como una razón geométrica. Pero, ¿qué entendemos por razones matemáticas?

Razones matemáticas

El termino “razón” en matemática significa una relación específica de un numero como el punto medio respecto a dos extremos.

Razon aritmetica

En la imagen se muestra que la razón aritmética de 2 y 8 es 5, porque 5 esta a la misma distancia entre ambos si sumamos sus distancias:
2 + 3 = 5 y 5 + 3 = 8

Para la razón aritmética (b) de 2 números (a) y (c): b = ( a + c ) / 2
La razón aritmética entonces es el simple promedio (suma) entre dos números.

Razón geométrica

La razón geométrica es similar, pero esta basada en múltiplos comunes que relacionan su razón a los otros dos números. Por ejemplo, la razón geométrica de 1 y 9 es 3, porque 3 esta en la misma distancia de ambos si se multiplica su distancia:
1*3 = 3 y 3 * 3 = 9

Así 1 es a 3 como 3 es a 9.
Para la razón geométrica (b) de dos números (a) y (c), b es la raíz cuadrada de a por c.

La razón Dorada

La razón Dorada es una razón geométrica muy específica. En la razón geométrica de arriba, vimos las longitudes siguientes de segmentos de línea en una línea de números: 1,3,9.

Aquí, 1 x 3 = 3 y 3 x 3 = 9, pero 3 + 3 = 6, no 9. La razón Dorada impone el requerimiento adicional que los dos segmentos que definen la razón también deben sumarse a la longitud del segmento completo de la línea:

Esto solamente ocurre en un punto, que como usted puede ver arriba es solo un poco menos que 5/8, o 0.625. El punto exacto de la razón Dorada es 0.6180339887..., donde :
A es a B como B es a C y B + C = A

El numero 5 esta intrínsecamente relacionado con Phi y a la serie Fibonacci.
Phi puede ser derivado de varias formulas basadas en el numero 5. La más tradicional, basada en la construcción geométrica de phi es: Phi = (v5+1)/2

Esta formula también puede ser expresada en cincos como sigue: F = 5 ^ .5 * .5 + .5

Otra formula para phi basada enteramente en cincos, es: F= v((5+v5)/(5-v5))

Y, los términos de la representación de arriba de phi también pueden ser expresados de otra forma que involucra al 5: (5+v5) x (5-v5) = 5 + 5 + 5 + 5

Pentágono

Tome un pentágono con cinco lados iguales y conecte todos sus puntos para formar una estrella de cinco puntas. Las razones de la longitud de los segmentos de línea resultantes están todos basados en phi.

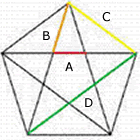
En la imagen notamos que A:B como B:C como C:D =0.618033 (el inverso de phi)

Puedes computar un numero n de la serie Fibonacci (fn) usando phi y la raíz de 5: fn = Fn / 5½

5 también el quinto numero de Fibonacci, en 0,1,1,2,3,5

5 aparece en cuerpo humano, que tiene proporciones basadas en phi. 5 extensiones del torso, 1 cabeza, 2 brazos, 2 piernas. 5 extensiones de cada brazo y piernas en 5 dedos cada una. 5 aperturas en la cara y 5 sentidos: vista, oído, gusto, tacto, olfato.

Espirales Áureas

Imagen de Grupo Implosión - Dan Winter

Si sumamos los cuadrados de cualquier serie de los números Fibonacci, van a igualar el ultimo numero Fibonacci usado en la serie por el siguiente numero Fibonacci. Esta propiedad se ve en la espiral dorada que se encuentra desde la concha del molusco Nautilus a las galaxias: 12 + 12 + 22 + 32 + 52 = 5 x 8,
entonces, 12 + 12 + . . . + F(n)2 = F(n) x F(n+1)

Nota: la espiral basada en la serie de Fibonacci es ligeramente diferente de la espiral perfecta generada por Phi por las aproximaciones en la serie a Phi. (1, 1, 2, 3, 5, 8 y 13 producen proporciones de 1, 2, 1.5, 1.67, 1.6 y 1.625)

Las espirales alternas en las plantas ocurren en los números Fibonacci. Las plantas ilustran la serie de Fibonacci en el número de sus hojas, en el arreglo de las hojas alrededor del tallo y en la posición de las hojas, las secciones y las semillas. Podemos ver en la imagen el centro de un girasol que ilustra este principio como 55 espirales en el sentido de las manecillas del reloj y 89 en contra.

Podemos apreciar en esta conifera 8 espirales girando hacia un lado y 13 girando hacia el lado contrario. 8 y 13 son dDos de ls numeros de la secuencia Fibonacci. El principio de la creación de la gravedady de la vida. Vea el trabajo de Dan Winter al respecto aquí.

La concha del Nautilus y la espiral dorada en la imagen de abajo

Notamos la espiral dorada que marca la pauta de distribucion de los elementos en esta pintura. Vea nuestra sección de Arte.

Observa las espirales áureas en esta imagen. ¿Puedes ver cuántas giran haciar la derecha y cuántas hacia la izquierda?

http://www.psicogeometria.com/matematica.htm

El número Phi (fi) - 1.618033... lo podemos derivar de tres maneras: matemáticamente, geométricamente y por secuencia numérica.

Phi es uno de los dos grandes tesoros de la geometría. Johannes Kepler dijo que el primero es phi y el segundo es el Teorema de Pitágoras. En un triangulo, phi forma las dimensiones de la gran pirámide de Egipto. Con una regla y un compás podemos crear el rectángulo áureo. El rectángulo áureo se usa extensivamente en la arquitectura como en el Partenón griego. Phi también define las dimensiones del pentágono.

Los cinco sólidos platónicos, llamados así porque Platón fue el primero en escribir sobre ellos, tienen la característica de ser cuerpos tridimensionales que tienen caras regulares. Las caras regulares son caras o polígonos cuyos lados son iguales, como el triangulo equilátero, el pentágono y el cuadrado. Los cinco sólidos platónicos son la base de la construcción de la materia y los encontramos relacionados con nuestra conciencia a través de los cinco centros de comando. Estos son: el tetraedro (4 caras triangulares), el hexaedro o cubo (6 caras cuadradas), el octaedro (8 caras triangulares), el icosaedro (20 caras triangulares), y el dodecaedro (12 caras pentagonales).

(arriba) imágen por Grupo Implosión - Dan Winter

Además podemos relacionar cada uno de los cinco sólidos platónicos con las retículas terrestres y los Cinco Elementos de la tradición china, como sigue (de izquierda a derecha):

Tetraedro: Fuego - Barisfera

Hexaedro: Tierra - Litosfera

Octaedro: Aire - Atmósfera

Icosaedro: Agua - Hidrósfera

Dodecaedro: Gaia, Madera - Biosfera

Los matemáticos han encontrado que la Proporción Dorada se encuentra presente en tres de estos cinco sólidos platónicos: el octaedro, el dodecaedro y el icosaedro.

En el interior del dodecaedro y del icosaedro podemos dibujar tres rectángulos dorados. Están dispuestos de tal forma que sus esquinas tocan todos los puntos centrales de las caras pentagonales del dodecaedro y todos los vértices del icosaedro. Además, es importante mencionar que si extendemos los vértices del dodecaedro o del icosaedro obtenemos su reciproco. Es decir, si extiendo los vértices del dodecaedro obtengo un icosaedro y si continúo haciendo lo mismo obtengo un dodecaedro en una siguiente dimensión y así infinitamente hacia adentro o infinitamente hacia fuera. Este principio de recurrencia fractal nos marca la pauta de creación en el universo.

En la animación de abajo podemos ver la Estrella Madre o Estrella de Metatron. Son los cinco sólidos platónicos contenidos uno dentro de otro en un espacio de embonacion perfecto. De adentro hacia afuera podemos observar de amarillo el dodecaedro, de azul claro el icosaedro, de verde el octaedro, de rosa el tetraedro y de negro el hexaedro o cubo. Este patrón de anidacion permite a las ondas/eventos embonar hacia el centro de gravedad de la materia sin auto cancelase ni cancelar a otras ondas/eventos. En Psicogeometria utilizamos una técnica terapéutica que nos permite arreglar los eventos dolorosos de nuestra vida en un patrón similar para que el evento pueda sortearse en nuestro escenario interno de conciencia y ordenarse de tal forma que no genere una confrontación interna. La solución del conflicto no radica únicamente en cobrar conciencia del conflicto sino en disponer este conflicto en una estructura geométrica que nos reestablezca nuestra paz interna.

animación por Grupo Implosión -Dan Winter

En esta imagen podemos notar la manera en la que la proporción dorada gobierna los trazos del pentágono. A: B como B:C como C:D a razón de 0.618033 (el inverso de Phi).

En esta imagen observamos la creación de un rectángulo dorado. El ancho respecto de la altura es 1.618033... veces más grande.

Toroide Fractal  Imagen por Grupo Implosión (Dan Winter)

Hemos mencionado que la creación se originó en el vacío y del vacío surgió la Ley de Unidad. Esta ley de Unidad, consagrada en el tubo toroide, es creadora de nuestra conciencia cuando posicionamos en alguno de sus extremos nuestro foco atencional y creamos otro tubo toroide. En el patrón del Génesis es el segundo día de creación del que habla la Biblia y en el que se crea la luz. Es el surgimiento de la aparente dualidad y el surgimiento verdadero de la Ley de Tres Geométrica. Con este movimiento del espíritu surge la Vesica Piscis. La forma que tiene esta figura es la misma forma de todo aquello por donde entra o sale luz o energía/materia. La forma de nuestros ojos, la vagina, la uretra, etc. son ejemplo de ello. En esta figura esta contenida la raíz cuadrada de 2, 3 y 5. Abordamos profundamente este estudio de la Creación de la Conciencia en el Curso Uno de Psicogeometria: Principios geométricos de la Conciencia.

La espiral dorada es una de las formas que por naturaleza expresan la armonía perfecta del universo. Esta imagen está construida a partir de triangulos dorados y la podemos observar con toda claridad en la concha del Nautilus (ver más en nuestra sección de matemática). La espiral dorada es el camino que siguen las ondas (la vida) para salir o entrar hacia el punto cero: el origen de la vida, el vacío.

El Árbol de la Vida es una de las figuras geométricas más antiguas que han sido usadas por la humanidad. Geometricamente esta formado por un tetraedro, un hexaedro y un dodecaedro. Los cabalistas se han dedicado a su estudio. Representa un código que nos da las pautas de evolución que se ha mantenido a voces secretas en los círculos del poder. Cada uno de los vértices en el Árbol de la Vida, simboliza para los cabalistas una sefira. Cada sefira es un atributo de Dios. En Psicogeometria estudiamos el origen y las implicaciones geométricas de esta figura. No solamente desde la perspectiva cabalista sino desde un ángulo psicológico vinculado a nuestro cuerpo por medio de tres sistemas: el digestivo, el endocrino y el nervioso. El eneagrama de la tradición sufi y derviche esta contenido en esta figura. Exponemos ampliamente este código de evolución en el Curso Dos de Psicogeometria: Psicotipos en el Árbol de la Vida.

El proceso de creación de la vida ha sido descrito a lo largo de la humanidad por diferentes culturas. Algunas han sembrado su conocimiento en una síntesis geométrica. Los trazos como los que exponemos abajo se han encontrado en todas las latitudes y en todos los tiempos.

Semilla de la Vida - Estrella Tetraedrica  Imagen por Grupo Implosión (Dan Winter)

La Semilla de la Vida es el principio del Génesis. El Huevo de la Vida son los trazos que surgen de dos tetraedros imbricados y nos habla de la manifestación de la Ley de Octava Geométrica. La Fruta de la Vida es la plantilla de la tercera dimensión en la que superponemos los sólidos platónicos. La Estrella de Metatron es la estrella de vida que surge cuando imbricamos armónicamente todos los sólidos platónicos y creamos una Estrella Madre. Esta estrella contiene y es capaz de organizar la frecuencia y la velocidad de las ondas/eventos. Finalmente, como expresión última, de la extensión de los trazos de la Semilla de la Vida surge la Flor de la Vida. La Flor de la Vida es la expresión mas refinada de la creación. Contiene holográmicamente todos los sólidos platónicos y todas las figuras mencionadas.

En el Curso uno de Psicogeometria trazamos estas figuras y creamos mayor interconectividad entre los hemisferios cerebrales. La Flor de la Vida nos invita a despertar nuestra visión objetiva de la realidad.

La Fruta de la Vida

El Huevo de la Vida

La Semilla de la Vida
http://www.psicogeometria.com/geometria2.htm