|
|
www.librosmaravillosos.com/historiatiempo/capitulo10.html
En el capítulo anterior discutimos por que vemos que el tiempo va hacia
adelante: por que ... La solución de Gödel y el espacio-tiempo de las cuerdas
cósmicas ...
www.librosmaravillosos.com/.../capitulo05.html
La solución de Gödel exigía una constante cosmológica, que puede existir o no
en la naturaleza, ... Fuera de una cuerda cósmica, el espacio-tiempo es plano.
es.wikipedia.org/wiki/Viaje_a_través_del_tiempo
Para los viajes a través del tiempo en la ciencia ficción y literatura, véase Viaje ...
las partículas materiales al moverse a través del espacio-tiempo se mueven
hacia .... como universo de Gödel, fue hallada por Kurt Gödel, aunque dicha
solución .... cuerdas cósmicas propuesto por Richard Gott se basa en la solución
de las ...
es.wikipedia.org/wiki/Curva_cerrada_de_tipo_tiempo
El cono de luz inferior es característico de un espacio-tiempo plano. .... La
solución del universo rotatorio de Gödel, la verosimilitud de la cual en su
momento ... un mecanismo para crear curvas temporales cerradas usando
cuerdas cósmicas.
https://www.examtime.com/.../908393-agujeros-de-gusano-y-viajes-en-el-tiempo-mind_maps
Otro es un espacio-tiempo que contiene dos cuerdas cos-micas en ... La solución
de Gödel y el espacio-tiempo de las cuerdas cósmicas comienzan tan ...
www.gabitos.com/.../template.php?nm=1420986894
hace 1 día ... La solución de Gödel y el espacio-tiempo de las cuerdas cósmicas comienzan
tan distorsionados que el viaje al pasado es siempre posible.
www.gabitos.com/.../template.php?nm=1420914389
hace 1 día ... Stephen Hawking en su obra Historia del Tiempo, dice: ... La solución de Gödel y
el espacio-tiempo de las cuerdas cósmicas comienzan tan ...
https://books.google.com.ar/books?isbn=8499209920
El gran matemático Kurt Gödel descubrió una solución para las ecuaciones de la
... nos cuenta Hawking, que permitió un nuevo espacio-tiempo en el que viajar
hacia el ... del tiempo deriva de una combinación especial de cuerdas cósmicas.
www.elcultural.es/revista/ciencia/Viaje-en-el-tiempo/34043
31 Ene 2014 ... La solución de Gödel requería una constante cosmológica, cuya ... El espacio-
tiempo de la cuerda cósmica contiene materia que tiene ...
wicho214.blogspot.com/.../capitulo-10-agujeros-de-gusano-y-viajes.html
11 Jun 2009 ... En el capítulo anterior discutimos porque vemos que el tiempo va hacia ... La
solución de Gödel y el espacio-tiempo de las cuerdas cósmicas ...
|
|
|
 Primeira
Primeira
 Anterior
2 a 9 de 9
Seguinte
Anterior
2 a 9 de 9
Seguinte
 Última
Última

|
|
|
investigacionyanalisis...
curva-de-tipo-tiempo-
417 × 389 - 26k - jpg |

eltrasguprobabilista.w...
el viaje en el tiempo.
400 × 514 - 349k - png |

3djuegos.com
describen espacios-tiempo
575 × 295 - 152k - png |

taringa.net
teoria de las cuerdas
400 × 320 - 13k - jpg |

jmacosta.galeon.com
Estas cuerdas pueden tener
457 × 430 - 38k - jpg |

taringa.net
Utilización de una cuerda
599 × 548 - 116k - bmp |
es.wikipedia.org
un espacio-tiempo plano.
200 × 250 - 1k - png |

taringa.net
viajar en el tiempo
400 × 292 - 19k - jpg |

jmacosta.galeon.com
del espacio y del tiempo
422 × 480 - 25k - jpg |

es.wikipedia.org
Utilización de los agujeros de
220 × 165 - 22k - png |

gabitos.com
Una cuerda puede hacer algo
500 × 422 - 69k - jpg |

es.wikipedia.org
Representación tridimensional
380 × 274 - 31k - png |

librosmaravillosos.com
Historia del Tiempo - Stephen
600 × 150 - 81k - jpg |

es.slideshare.net
Cuerda cósmica Objeto largo y
638 × 902 - 94k - jpg |

taringa.net
región de espacio-tiempo
500 × 351 - 54k - jpg |

es.slideshare.net
dividen al espacio-tiempo
728 × 943 - 96k - jpg |

taringa.net
viajes atraves del tiempo
737 × 611 - 165k - jpg |

kronicasdeloimpensable...
puertas espacio-temporales
893 × 644 - 53k - jpg |

es.slideshare.net
Historia del Tiempo: Del Big
728 × 943 - 123k - jpg |

es.slideshare.net
Historia del Tiempo: Del Big
728 × 942 - 187k - jpg |
|
|
|
|
|
Viaje a través del tiempo
De Wikipedia, la enciclopedia libre
|
|
Este artículo o sección tiene un estilo difícil de entender para los lectores interesados en el tema.
Si puedes, por favor edítalo y contribuye a hacerlo más accesible para el público general, sin eliminar los detalles técnicos que interesan a los especialistas. |

Representación tridimensional del futuro causal y el pasado causal de un evento. El evento en cuestión es el vértice central del punto de vista de la luz (azul) donde se unen el cono superior y el inferior. Todos los puntos dentro del cono superior son su futuro causal, todos los puntos en el cono inferior son su pasado, el eje vertical (rojo) representa el avance del tiempo y las dos flechas horizontales dos direcciones espaciales.
El viaje a través del tiempo es un concepto de desplazamiento hacia delante o atrás en diferentes puntos del tiempo, similar a como se hace un desplazamiento en el espacio. Además, algunas interpretaciones de viaje en el tiempo sugieren la posibilidad de viajes entre realidades o universos paralelos.
Este artículo analiza la posibilidad teórica y técnica de viajes en el tiempo, y la posibilidad de que existan paradojas asociadas a dicho viaje a través del tiempo (por ejemplo evitar el nacimiento de nuestros propios antepasados). De acuerdo a algunos argumentos, el viaje en el tiempo en la experiencia cotidiana se experimenta a 1 segundo por segundo hacia el futuro.
Los viajes a través del tiempo en la física[editar]
De acuerdo con la descripción convencional de la teoría de la relatividad, las partículas materiales al moverse a través del espacio-tiempo se mueven hacia adelante en el tiempo (hacia el futuro) y hacia un lado u otro del espacio. El hecho de que la energía total y la masa sean positivas está relacionado con el hecho de que las partículas se muevan hacia el futuro.
Un aspecto comprobado experimentalmente de la teoría de la relatividad es que viajar a velocidades cercanas a la velocidad de la luz ocasiona una dilatación del tiempo, por la cual el tiempo de un individuo que viaja a esa velocidad corre más lentamente. Desde la perspectiva del viajero, el tiempo "externo" parece fluir más rápidamente, causando la impresión de que el individuo hizo un viaje a través del tiempo. Sin embargo, este fenómeno en sí mismo, no es lo que suele denominarse como viaje a través del tiempo.
El concepto de viaje en el tiempo ha sido frecuentemente utilizado para examinar las consecuencias de teorías físicas como la relatividad especial, la relatividad general y la teoría cuántica de campos, aunque no existe evidencia experimental del viaje en el tiempo y existen razones teóricas importantes para considerar posible la existencia de cierto tipo de viaje a través del tiempo. En cualquier caso, las teorías actuales de la física no permiten ninguna posibilidad de viajar en el tiempo.
La posibilidad de los viajes en el tiempo[editar]
La teoría especial de la relatividad de Albert Einstein (y por extensión la teoría general) permite explícitamente un tipo de dilatación temporal que ordinariamente se podría denominar “viaje en el tiempo”. La teoría sostiene que relativamente a un observador estacionario, el tiempo parece fluir más lentamente para los cuerpos que se desplazan rápidamente. Por ejemplo, un reloj que se desplaza parecerá correr más lento; al incrementar su velocidad y acercarse a la velocidad de la luz parecerá haberse detenido completamente. Sin embargo, este efecto sólo hace posible el “viaje en el tiempo” hacia adelante en el futuro, nunca hacia atrás. Este tipo de viaje no es típico de la ciencia ficción, y no se tiene ninguna duda acerca de su existencia; sin embargo, de aquí en adelante “viaje en el tiempo”, propiamente dicho, se referirá al recorrido con algún grado de libertad hacia el pasado o el futuro.
Muchos científicos consideran que el viaje a través del tiempo propiamente dicho es imposible. Esta opinión se ve reforzada por un argumento basado en la navaja de Occam. Cualquier teoría que permita el viaje en el tiempo requiere que algunas situaciones relacionadas con la causalidad (o, en su caso, retrocausalidad) sean resueltas. ¿Qué pasaría si alguien trata de viajar en el tiempo y mata a su propio abuelo? (Ver la “paradoja del abuelo”).
Además, en la ausencia de cualquier evidencia experimental de la posibilidad del viaje en el tiempo, es teóricamente más simple suponer que no puede ocurrir. De hecho, el físico Stephen Hawking ha sugerido que la ausencia de turistas del futuro constituye un fuerte argumento en contra de la existencia del viaje en el tiempo (véase Conjetura de protección de la cronología). Eso sería una variante de la paradoja de Fermi (“si no hay visitantes extraterrestres es porque los extraterrestres no existen”), en la que se hablaría de “viajeros del tiempo” en lugar de “visitantes extraterrestres”. Dadas estas circunstancias, otros sugieren —a los que sostienen la posición de Hawking— que en el caso de que en un futuro el ser humano pudiese viajar al pasado, éste no podría regresar a un espacio temporal anterior al momento de la puesta a punto de la hipotética máquina del tiempo que lo permitiese.
También se ha sugerido que al viajar al pasado se estaría “creando” un universo paralelo y no se viajaría al propio pasado sino a una copia de éste, pero con una diferencia: la existencia de un turista temporal. De este modo se tendría dos espacios temporales simultáneos: uno donde aparece un turista del tiempo y otro donde no aparece. Ésta sería una hipótesis para discutir la paradoja de “Si mañana planeo un viaje a hoy para decirme ‘hola’, ¿por qué hoy no tengo un doble a mi lado diciéndome ‘hola’?” Sin embargo, asumiendo que el viaje temporal no es posible, también resulta interesante para los físicos la pregunta de por qué y qué leyes físicas lo impiden.
La posibilidad de las paradojas temporales[editar]
El principio de autoconsistencia de Novikov y cálculos recientes de Kip Thorne indican que simples masas pasando en el tiempo a través de agujeros de gusano no podrían generar paradojas, ya que no existen condiciones iniciales que induzcan una paradoja una vez que es introducido el viaje en el tiempo. Si sus resultados pueden ser generalizados sugerirían, curiosamente, que ninguna de las paradojas formuladas en las historias de viaje temporal puedan ser realmente formuladas en un nivel físico: es decir, que cualquier situación que se provoque en una historia de viaje temporal puede permitir muchas soluciones coherentes. Las circunstancias podrían sin embargo, tornarse casi increíblemente extrañas.
Los universos paralelos son una posibilidad teórica que evitaría la mayor parte de las paradojas relacionadas con viajes a través del tiempo. La interpretación de mundos múltiples de H. Everett sugiere que todos los eventos cuánticos posibles pueden ocurrir simultáneamente en historias exclusivas. Estas historias alternas o paralelas, formarían un árbol ramificado que simbolizaría todos los posibles resultados de cualquier interacción.
Debido a que todas las posibilidades existen, cualquier paradoja puede ser explicada al ocurrir los eventos paradójicos en un universo diferente. Este concepto es frecuentemente utilizado en la ciencia ficción. Sin embargo, en la actualidad, los físicos creen que dicha interacción o interferencia entre estas historias alternativas no es posible (véase la conjetura de protección cronológica de Stephen Hawking).
Paradoja de la inexistencia de viajeros del tiempo[editar]
Si tenemos en cuenta que cada vez sabemos más de física cuántica y que la tecnología progresa a través del tiempo, se puede postular que deberíamos ser visitados por viajeros del tiempo, hecho no observado, y que puede ser considerado una paradoja. Para explicar esto, se ha postulado que esto puede indicar que la humanidad se extinguirá antes de descubrir la tecnología de viajar en el tiempo, lo que también se aplicaría a presuntos mundos en universos paralelos, porque ellos tampoco habrían desarrollado la tecnología para viajar entre universos.
Otra paradoja dice que aún siendo posible crear una máquina del tiempo dentro de cien años, esta no podría volver más atrás del momento en el que se construyó dicha máquina porque se tardaría más de cien años en crear una relación de tiempo de cien años. Dicho esto, se podría construir una máquina durante ciento diez años para regresar atrás en el tiempo cien años, pero no cuatrocientos. La única posibilidad sería, por ejemplo, que otra civilización hubiese construido una máquina mucho antes de nuestra existencia para así poder volver hasta el punto en el que se construyó, es decir, antes de haberse creado la tierra.[1]
Otras explicaciones menos convencionales y con características pseudocientíficas, son aquellas que postulan la existencia de viajeros temporales ocultos. Tales viajeros rehusarían manifestarse públicamente y actuarían como auténticos "turistas" temporales u observadores, sin, aparentemente, mayor injerencia en los asuntos de la humanidad actual, pero esta hipótesis sería, por supuesto, completamente indemostrable. Se ha alegado, también, que ciertos individuos podrían ser viajeros temporales más o menos ocultos, mencionándose entre ellos a notables inventores o literatos; no obstante ninguna de las pruebas aducidas resulta convincente. Del mismo modo supuestos "visitantes" de otras épocas han probado ser, en todos los casos, fraudes o productos de informes inexactos. Ciertos autores mencionan como evidencia del viaje temporal los vestigios de civilizaciones con una tecnología muy similar a la nuestra, como por ejemplo el Mecanismo de Antiquitera que data de entre los años 82 y 65 a.C o las Baterías de Bagdad, procedentes de la misma época. En todos estos casos la existencia de tales dispositivos tecnológicos puede ser explicada mucho mejor enmarcándolos en su contexto histórico.
Los equivalentes de viaje temporal y viaje a la velocidad de la luz[editar]
Se puede señalar que si alguien es capaz de mover información de un punto a otro más rápido que la velocidad de la luz, de acuerdo a la relatividad especial, equivale a que un observador percibe una transferencia de información hacia el pasado. Por otra parte, no se han propuesto mecanismos físicos que sugieran que esa posibilidad es técnicamente viable de acuerdo con la relatividad especial.
La teoría general de la relatividad por su parte ofrece algunas posibilidades teóricas adicionales. Esta teoría formulada por Einstein generaliza la teoría especial de la relatividad que hemos considerado hasta ahora. Esta teoría además de su mayor generalidad es capaz de describir adecuadamente la gravedad desde un punto de vista relativista. La interpretación de la gravedad que hace esta teoría es que la materia “curva” el espacio y el tiempo que se encuentra a su alrededor. Estas propiedades de la curvatura abren nuevas posibilidades para el viaje a través del tiempo:
- Teóricamente existen soluciones de las ecuaciones que incluyen líneas temporales que se curvan alrededor de un círculo y se reconecten con su propio pasado. La primera y más famosa de estas soluciones, conocida como universo de Gödel, fue hallada por Kurt Gödel, aunque dicha solución atribuye al universo ciertas características físicas que no parecen corresponderse con las de nuestro universo. La teoría de la relatividad general en sí misma no prohíbe la curva temporal cerrada o curva cerrada de tipo tiempo (traducción literal del inglés closed timelike curve), que puede llegar a aparecer en las soluciones de las ecuaciones. Sin embargo, la mayoría de los físicos cree que es necesario explicar correctamente las condiciones si se pretende una descripción completa y realista, es decir, las condiciones adicionales, las cuales, de no cumplirse, eliminarían la posibilidad de las curvas temporales cerradas debido a sus implicaciones paradójicas, por ejemplo aquellas que se relacionan con la hipotética retrocausalidad (la posibilidad que tendría el viajero al pasado de influir en el mismo, con los consiguientes resultados en el presente, según vemos contempla la paradoja del abuelo).
- Existe además la posibilidad de que diferentes regiones del espacio inicialmente separadas entren en contacto mediante la formación de un "puente" o "agujero de gusano". En general estas requerirían pasar por estados topológicamente no equivalentes que involucren "rasgado" del espacio-tiempo, posibilidad recientemente considerada en la teoría de cuerdas y explicado divulgativamente por Brian Greene en El universo elegante.
Viajes hacia el futuro[editar]
En realidad todas las partículas viajan continuamente hacia el futuro, ya que el tiempo fluye siempre en la misma dirección, y el paso del tiempo es sólo el movimiento hacia el futuro, en los términos en que los describe la teoría de la relatividad. Sin embargo, el flujo de avance hacia el futuro puede ser algo lento para la duración de la vida humana. Para conocer lo que sucederá mañana, tan sólo se tiene que esperar un día sin necesidad de hacer un desplazamiento en el tiempo, pero conocer el futuro lejano y, por ejemplo, conocer a nuestros tataranietos o contemplar la civilización dentro de mil años es diferente. El efecto relativista de la dilatación del tiempo ofrece, al menos teóricamente, la posibilidad de viajar al futuro evitando envejecer.
En la paradoja de los gemelos, los dos hermanos se encontraban en el futuro pero habían recorrido caminos diferentes, y uno de ellos, el que se había acelerado hasta viajar a gran velocidad en una nave espacial, había reducido su envejecimiento. Aunque el tiempo propio medido por un observador en movimiento respecto a otro será menor y la magnitud del efecto viene dada por la velocidad (v) del observador en movimiento y la velocidad de la luz (c):

Sin embargo, desde el punto de vista del propio observador en movimiento, él mismo está en reposo y él no percibe que esté envejeciendo más lentamente. De hecho, para este observador en movimiento sería el observador en reposo quien estaría envejeciendo más rápidamente. Sólo en situaciones en que aparecen sistemas de referencia no inerciales en que los dos observadores se encuentren puede darse una situación en que ambos observadores coincidan en que uno de ellos dos ha envejecido más lentamente.
Si consideramos un observador que se aleja en una nave con una velocidad que sea un 90% de la luz, el tiempo transcurrido en la Tierra, ignorando el efecto de Dilatación gravitacional del tiempo para simplificar, sería unas 2,30 veces más lento según un observador en la Tierra. Es decir, que incluso yendo a esta altísima velocidad sólo ganaríamos un modesto factor dos en nuestro viaje al futuro. Para hacer viajes interesantes al futuro necesitamos que la nave vaya a velocidades realmente considerables.
Para viajar a futuros más lejanos ‘sólo’ sería necesario hacer que la velocidad fuera aún más cercana a la de la luz. Nuestra nave viajando a gran velocidad en un camino con origen y regreso a la Tierra es una máquina del tiempo para viajar al futuro que, en la medida en que se tenga la capacidad de incrementar su velocidad, puede transportar a un viajero sin envejecerlo a cualquier tiempo posterior.
Es evidente que la construcción de una nave, de este tipo de máquina del tiempo, actualmente está fuera de las posibilidades técnicas de nuestra civilización. Sin embargo, hay ejemplos que demuestran que la idea es correcta. En la Tierra recibimos partículas que vienen del centro de nuestra galaxia a distancias que la luz tarda miles de años en recorrer. Es decir, fueron producidas hace miles de años terrestres. Sin embargo, estas partículas no pueden resistir un viaje ni siquiera de un minuto, ya que se desintegran en cuestión de segundos después de haber sido creadas. ¿Cómo explicar esta paradoja? Haciendo uso de la dilatación temporal: las partículas han sido aceleradas a velocidades tan cercanas a la de la luz que sólo habían envejecido segundos mientras que en la Tierra transcurrían miles de años.
Una máquina del tiempo de este tipo es unidireccional, es decir; sólo permite viajar al futuro. Esto, sin duda, limita mucho el encanto del viaje. No sería posible, por ejemplo, viajar al futuro para echar un vistazo a los resultados de un juego de azar y volver atrás. La posibilidad de viajar al pasado, que es la que hace realmente interesante una máquina del tiempo, es muy dudosa y puede afectar a principios muy generales. Sin perder de vista estas restricciones, en otro apartado se trata cómo se podría transformar una máquina del tiempo unidireccional basada en la paradoja de los gemelos en una máquina del tiempo de dos direcciones usando un ‘agujero de gusano’.
|
|
|
|
|
Métodos propuestos para su realización[editar]
Utilización de los agujeros de gusano[editar]
Una máquina de viaje

Representación 2D de un agujero de gusano.
temporal propuesta que utilice un agujero de gusano funcionaría (hipotéticamente) de la siguiente manera: se crea de alguna manera un agujero de gusano. Un extremo del túnel es acelerado a una velocidad cercana a la de la luz, quizás con una nave espacial avanzada, y entonces se regresa de vuelta al punto de origen. Debido a la dilatación temporal (debida a la velocidad), el extremo acelerado del túnel ha envejecido menos que el extremo estacionario (desde el punto de vista de un observador externo).
Sin embargo, el tiempo se ve diferente a través del túnel que fuera de él: dos relojes sincronizados puestos en cada extremo del túnel se mantendrán siempre sincronizados (desde el punto de vista de un observador dentro del túnel), sin importar la diferencia de velocidad.
Esto significa que un observador que entrara al extremo acelerado, saldría por el extremo estacionario cuando el extremo estacionario tenía la misma edad que el extremo acelerado en el momento antes de entrar. Por ejemplo, si antes de entrar al agujero de gusano el observador notó que el reloj en el extremo acelerado mostraba 2006 mientras que el reloj en el extremo estacionario ya decía 2007, entonces el observador podría salir por el extremo estacionario cuando el reloj estacionario todavía decía 2006.
Una limitación significativa de tal máquina es que sólo es posible viajar hacia el pasado en el punto inicial cuando fue creada la máquina; en esencia, se considera más como un pasaje a través del tiempo que un dispositivo que se mueve a través del tiempo: no permite que la propia tecnología en sí misma viaje a través del tiempo.
Esto puede permitir una explicación alternativa a la paradoja de Hawking: algún día se podrá construir una de estas máquinas al pasado, pero todavía no han sido construidas, por lo que los turistas temporales nunca podrán llegar a nuestro presente.
Crear un agujero de gusano de un tamaño apropiado para una nave macroscópica, mantenerlo estable y mover uno de sus extremos con la nave requeriría un nivel significativo de energía en un orden mucho mayor que la cantidad de energía que un sol como el nuestro puede generar en todo su periodo de vida. La creación de un agujero de gusano también requeriría la existencia de una sustancia llamada “materia exótica”, que —aún cuando no es imposible— no se sabe si existe en formas útiles para la generación de un agujero de gusano (Ver por ejemplo el efecto Casimir).
Por lo tanto es inverosímil que tal dispositivo sea construido, incluso con tecnología altamente avanzada. Por otra parte, agujeros de gusano microscópicos aún pueden ser útiles para enviar información de regreso al pasado a través del tiempo.
En 1993, Matt Visser argumentó que los dos extremos de un túnel de gusano con tal diferencia temporal inducida no podrían ser reunidos sin generar un campo cuántico y unos efectos gravitacionales que provocarían que el túnel colapsara o que los dos extremos se repelieran. [1]
Debido a esto, los dos extremos no podrían acercarse lo suficiente porque tendría lugar una violación de la causalidad. Sin embargo, en un paper de 1997, Visser conjeturó que la compleja configuración de un “anillo Roman” (así nombrado en honor a Tom Roman) de un número N de agujeros de gusano alineados en un polígono simétrico podría actuar como una máquina del tiempo, aunque concluye que esto no sería tanto un defecto en la teoría clásica de la gravedad cuántica, sino más bien la prueba de que es posible violar la causalidad. [2]
Utilización de cilindros rotatorios gigantescos[editar]
Otra teoría, desarrollada por el físico Frank J. Tipler, implica un cilindro rotatorio. Si un cilindro es lo suficientemente largo y denso, y gira lo suficientemente rápido en relación a su eje longitudinal, entonces una nave que volara alrededor del cilindro en una trayectoria espiral podría viajar atrás en el tiempo (o hacia adelante, dependiendo del sentido del movimiento de la nave). Sin embargo, la longitud, la densidad y la velocidad requerida son tan grandes que la materia ordinaria no es suficientemente fuerte para construirla.
Utilización vórtices de luz coherente (láser)[editar]
Ronald Mallett ha planteado crear vórtices láser envolventes e incluyentes de los objetos a cronotransportar, su idea se basa en la Teoría General de la Relatividad, más exactamente en el postulado por el cual la energía (en este caso la luz) no solo es curvada por la gravedad sino que puede tener efectos másicos que curvan al tejido espacio-temporal, haciendo arrastres de marco y curvas cerradas de tipo tiempo.
Utilización de una cuerda cósmica[editar]
Se puede construir un dispositivo similar a partir de una cuerda cósmica, que es un tipo de materia exótica especial, cuya existencia es postulada hipotéticamente en diversas teorías físicas especulativas. Las energías involucradas para interactuar con ellas serían probablemente prohibitivamente altas y seguramente constituirían una posibilidad tecnológicamente inviable.
El dispositivo mediante cuerdas cósmicas propuesto por Richard Gott se basa en la solución de las ecuaciones de la relatividad general para ese tipo de materia exóticas. De acuerdo con el esquema de Gott serían necesarias dos cuerdas cósmicas moviéndose en direcciones opuestas. Al seguir una trayectoria cerrada que rodee las cuerdas se logra el viaje en el tiempo. Una característica notable de esta solución es que el viaje en el tiempo es sólo posible para los observadores dentro de una cierta región del espacio-tiempo. Una vez las cuerdas se han alejado lo suficiente el mecanismo ya no puede ser usado para realizar un viaje en el tiempo.
Utilización de un núcleo atómico pesado[editar]
El físico y escritor de ciencia ficción, Robert L. Forward sugirió que una aplicación ingenua de la relatividad general a la mecánica cuántica permitiría construir una máquina del tiempo. Un núcleo atómico pesado situado dentro de un fuerte campo magnético podría alargarse hasta formar un cilindro, cuya densidad y rotación serían suficientes para viajar en el tiempo. Los rayos gamma proyectados podrían permitir enviar información (aunque no materia) de regreso al pasado. Sin embargo, él precisó que hasta que no tengamos una sola teoría que combine la relatividad y la mecánica cuántica, no tendremos idea si tales especulaciones son absurdas.
Utilización del entrelazamiento cuántico[editar]
Los fenómenos de la mecánica cuántica tales como el teletransporte cuántico, la paradoja EPR (nombrada por las iniciales de Albert Einstein, Boris Podolsky y Nathan Rosen), o entrelazamiento cuántico puede parecer que genera un mecanismo que permite la comunicación FTL (faster than light: más rápida que la luz) o viaje temporal. De hecho algunas interpretaciones de la mecánica cuántica (tales como la interpretación de Bohm) presumen que las partículas intercambian información de manera instantánea para poder mantener la correlación entre ellas. Einstein se refería a este efecto como la “espeluznante [spooky] acción a distancia”.
Curiosamente, las reglas de la mecánica cuántica parecen impedir la transmisión de información útil por estos medios, y por lo tanto parece que no “permitiera” el viaje en el tiempo o la comunicación FTL. Este hecho es exagerado y mal interpretado por cierto tipo de libros y revistas de pretendida divulgación científica acerca de los experimentos de teleportación. En la actualidad, la manera en que trabaja la mecánica cuántica para mantener la causalidad es un área muy activa de investigación científica.
Referencias[editar]
Referencias científicas[editar]
- Davies, Paul, Cómo construir una máquina del tiempo, ISBN 0-14-200186-4.
- Davies, Paul, About Time (‘Acerca del tiempo’) ISBN 0-684-81822-1.
- Gott, J. Richard, Time Travel in Einstein's Universe: The Physical Possibilities of Travel Through Time (‘El viaje en el tiempo en el universo de Einstein: las posibilidades físicas del viaje a través del tiempo’), ISBN 0-618-25735-7.
- Nahin, Paul J., Time Machines: Time Travel in Physics, Metaphysics, and Science Fiction (‘Máquinas del tiempo: el viaje en el tiempo en la física, la metafísica y la ciencia ficción’), ISBN 0-387-98571-9.
- Pickover, Clifford A., Time: A Traveler's Guide (‘Tiempo: guía para el viajero’), ISBN 0-19-513096-0
- Tipler, Frank J., Rotating Cylinders and the Possibility of Global Causality Violation (`Los cilindros rotativos y la posibilidad de una violación global de la causalidad’), Physical Review (D 9, 2203), 1974.
- Violat Bordonau, F. Problemas y paradojas del Viaje Temporal, 2007, Ed. Asesores Astronómicos Cacereños.
Obras sobre viajes en el tiempo en la literatura y en la historieta[editar]
- ASIMOV, Isaac: El fin de la eternidad.
- APPEL, Allen: Twice Upon a Time.
- Sebastian Bestard Molina, Operacion Cronos, Tradinco, 2013, ISBN 978-9974-98-964-4.
- APPLEGATE, Katherine: Animorphs.
- BENFORD, Gregory: Cronopaisaje.
- BORGES, Jorge Luis: El jardín de senderos que se bifurcan; El otro, en El libro de arena.
- CARPENTER, Richard: Catweazle.
- CRICHTON, Michael: Esfera y Rescate en el tiempo.
- DICKENS, Charles: A Christmas Carol.
- MAURIER, Daphne Du: The House on the Strand.
- FINNEY, Jack: Time and Again, From Time to Time, The Third Level y otras.
- FORDE, Jasper: Lost in a Good Book.
- HEINLEIN, Robert A.: Puerta al verano, All You Zombies, By His Bootstraps, The Cat Who Walks Through Walls, Farnham's Freehold y Time Enough For Love.
- HERRNSDORF, Alejandro: Manual de los viajes en el tiempo
- LAFFERTY, R. A.: Thus We Frustrate Charlemagne.
- LEM, Stanisław: Viaje séptimo (Podróż siódma), en Diarios de las estrellas (Dzienniki gwiazdowe).
- NIFFENEGGER, Audrey: La mujer del viajero en el tiempo.
- NIVEN, Larry: Rotating Cylinders and the Possibility of Global Causality Violation.
- POWERS, Tim: Las Puertas de Anubis.
- ROWLING, J. K.: Harry Potter y el prisionero de Azkaban.
- SWANWICK, Michael: Bones of the Earth.
- TARR, Judith; TURTLEDOVE, Harry: Household Gods (1999).
- TWAIN, Mark: Un yanqui en la corte del rey Arturo.
- VIOLAT BORDONAU, Francisco: El enigma del Cubo Baresch (2011).
- VONNEGUT, Kurt: Timequake (1997).
- WELLS, H. G.: La máquina del tiempo
- WILLIS, Connie: Doomsday Book (ISBN 0-553-56273-8) y To Say Nothing of the Dog.
- WILSON, Robert C.: A Bridge of Years (1991) y Los cronolitos (The Chronoliths, 2001).
- OESTERHELD, Héctor Germán: El Eternauta
- Kerstin Gier Kerstin: "Rubí (novela)"
Referencias filosóficas[editar]
Véase también[editar]
|
|
|
|
|
Universo de Gödel
De Wikipedia, la enciclopedia libre
El universo de Gödel o métrica de Gödel es una solución exacta de las ecuaciones de campo de Einstein de la relatividad general, propuesta por Kurt Gödel en 1949. Describe un tipo de universo o espacio-tiempo homogéneo lleno de materia pulverulenta en rotación.
Aunque no parece que el universo de Gödel describa un tipo de universo similar al nuestro, el trabajo de Gödel supuso un gran estímulo en la investigación teórica de búsqueda de soluciones exactas más complejas que las examinadas hasta entonces, caracterizadas por un muy alto grado de simetría. Más tarde Gödel generalizó su modelo para hacerlo compatible con la expansión del universo.
Forma de la métrica[editar]
La geometría del universo de Gödel viene representada por una espacio-tiempo 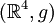 donde la métrica puede representarse en coordenadas pseudocartesianas (t, x, y, z) y unidades en las que c = 1 en la forma: donde la métrica puede representarse en coordenadas pseudocartesianas (t, x, y, z) y unidades en las que c = 1 en la forma:
Donde  es una constante, asociada a la vorticidad del flujo de materia, además esta vorticidad puede relacionarse con la densidad de materia de este universo, tal como se explica en la sección sobre el Contenido material. es una constante, asociada a la vorticidad del flujo de materia, además esta vorticidad puede relacionarse con la densidad de materia de este universo, tal como se explica en la sección sobre el Contenido material.
Formas alternativas[editar]
La métrica anterior puede escribirse como suma directa de una métrica que actúa sobre la subvariedad definida por (t, x, y) y otra métrica que actúa sobre las subvariedades unidimensionales dadas asociadas a la variación de z, es decir:
Para describir las propiedades de este espacio tiempo basta con restringirse a la subvariedad tridimensional que se obtiene suprimiendo la coordenada z. Para examinar las propiedades del espacio-tiempo frecuentemente se usan las coordenadas (T, R, φ, Z) relacionadas con las pseudocartesianas mediante las relaciones:
En estas nuevas coordenadas la métrica, ignorando la parte en Z toma la forma:
Propiedades generales del espacio-tiempo de Gödel[editar]
Contenido material[editar]
El universo de Gödel es una solución de las ecuaciones de Einstein con constante cosmológica repleto de materia pulverulenta, es decir, sin presión p = 0. El tensor gravitacional de Einstein Gij viene dado por:
Es sencillo ver que si se toma un valor de la constante cosmológica que cumpla:
Entonces el tensor de energía-impulso viene dado en las coordenadas (t, x, y, z):
Si 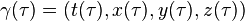 es la expresión de una curva usando el sistema de referencia asociado a las corodenadas de (1) y del tiempo propio entonces esa curva será geodésica si se cumple que: es la expresión de una curva usando el sistema de referencia asociado a las corodenadas de (1) y del tiempo propio entonces esa curva será geodésica si se cumple que:
Tensor de Riemann[editar]
De las potencialmente 55 componentes independientes del tensor de Riemann, en las mismas coordenadas usadas en la métrica (1), el tensor de Riemann se puede escribir a partir de sólo cuatro componentes diferentes de cero:
Grupo de isometría[editar]
El universo de Gödel tiene un grupo de isometría de dimensión 5, cuya acción de grupo opera transitivamente sobre toda la variedad, y por tanto, el universo de Gödel es un espacio-tiempo completamente homogéneo. El grupo de isometría consta de un subgrupo tridimensional de traslaciones:
Los otros subgrupos pueden representarse respectivamente en las coordenadas (t, x, y, z) y (T, R, φ, Z):
Una isometría general del universo de Gödel puede obtenerse combinando un número arbitrario de las anteriores transformaciones.
Propiedades particulares del espacio-tiempo de Gödel[editar]
Existencia de curvas temporales cerradas[editar]
Una propiedad matemáticamente interesante del universo de Gödel, es que alrededor de todo punto existen curvas temporales cerradas, lo cual físicamente supone que un observador puede viajar hacia el futuro y llegar a un punto de su pasado, repitiendo cíclicamente este movimiento. Esta propiedad sugiere que esta solución es físicamente poco realista o imposible. Lo sorprendente de la solución de Gödel es que a pesar de esta extraña propiedad el universo está formado por materia convecional no exótica y que si fuera posible dotar a ésta del movimiento de vorticidad que implica la ecuación tendríamos un universo con esta extraña propiedad causal.
De la forma del tensor métrico (1) se desprende que el vector  , que es de tipo espacial para valores de R pequeños pasa a ser de tipo luminoso para , que es de tipo espacial para valores de R pequeños pasa a ser de tipo luminoso para 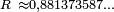 (es decir cuando (es decir cuando  ). Y en ese caso el covector ). Y en ese caso el covector  también es de tipo luz (tangente al cono de luz). El círculo con también es de tipo luz (tangente al cono de luz). El círculo con  es una curva luminosa cerrada, aunque no sea una curva geodésica. es una curva luminosa cerrada, aunque no sea una curva geodésica.
Examinando el sistema de referencia anterior, puede verse que la coordenada  puede omitirse; el espacio-tiempo de Gödel es el producto de un factor puede omitirse; el espacio-tiempo de Gödel es el producto de un factor 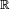 con una variedad pseudoriemanniana tridimensional de signatura -++. Dejando a un lago la coordenada con una variedad pseudoriemanniana tridimensional de signatura -++. Dejando a un lago la coordenada  , lo cual equivale a proyectar sobre la variedad tridimensional, la apariencia de los conos de luz cambia a medida que nos separamos del eje de simetría , lo cual equivale a proyectar sobre la variedad tridimensional, la apariencia de los conos de luz cambia a medida que nos separamos del eje de simetría 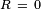 tal como muestra la siguiente figura: tal como muestra la siguiente figura:

Dos conos de luz (con sus correspondientes vectores de referencia) en una carta local cilíndrica para la un universo de Gödel formado por material pulvurulenta y con constante cosmológica. A medida que un observador se desplaza desde el eje de simetría central, los conos se "inclinan hacia adelante" y se "ensanchan". Nótese que las líneas coordenadas verticales (que representan líneas de universo de las partículas de materia pulvurulenta) siempre son de tipo temporal.
A medida que se consideran curvas más cercanas al radio del círculo mencionado anteriormente, los conos llegan a ser tangentes al plano coordenado 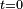 y también son tangentes a la curva cerrada de tipo luminoso: y también son tangentes a la curva cerrada de tipo luminoso:

Una curva cerrada de tipo luminoso en un universo de Gödel de materia pulvurulenta.
- Hawking, Stephen; and Ellis, G. F. R. (1973): The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press. ISBN 0-521-09906-4. La sección 5.7 contiene una discusión clásica sobre las CTC en el universo de Gödel..
http://es.wikipedia.org/wiki/Universo_de_G%C3%B6del |
|
|
|
|
Kurt Gödel
De Wikipedia, la enciclopedia libre
Kurt Gödel ([kuɹtˈgøːdl]), o también Kurt Goedel, (28 de abril de 1906 Brünn, Imperio austrohúngaro, actual República Checa – 14 de enero de 1978, Princeton, Estados Unidos) fue un lógico, matemático y filósofo austriaco-estadounidense.[1]
Reconocido como uno de los más importantes lógicos de todos los tiempos, el trabajo de Gödel ha tenido un impacto inmenso en el pensamiento científico y filosófico del siglo XX. Gödel, al igual que otros pensadores como Gottlob Frege, Bertrand Russell, A. N. Whitehead y David Hilbert intentó emplear la lógica y la teoría de conjuntos para comprender los fundamentos de la matemática. A Gödel se le conoce mejor por sus dos teoremas de la incompletitud, publicados en 1931 a los 25 años de edad, un año después de finalizar su doctorado en la Universidad de Viena.
El más célebre de sus teoremas de la incompletitud establece que para todo sistema axiomático recursivo auto-consistente lo suficientemente poderoso como para describir la aritmética de los números naturales (la aritmética de Peano), existen proposiciones verdaderas sobre los naturales que no pueden demostrarse a partir de los axiomas. Para demostrar este teorema desarrolló una técnica denominada ahora como numeración de Gödel, la cual codifica expresiones formales como números naturales.
También demostró que la hipótesis del continuo no puede refutarse desde los axiomas aceptados de la teoría de conjuntos, si dichos axiomas son consistentes. Realizó importantes contribuciones a la teoría de la demostración al esclarecer las conexiones entre la lógica clásica, la lógica intuicionista y la lógica modal.
Kurt Friedrich Gödel nació el 28 de abril de 1906 en Brünn, la capital de la Moravia Austrohúngara (actualmente Brno, República Checa) en una familia de etnia germana acomodada, compuesta por Rudolf August Gödel, hombre de negocios y administrador de una fábrica de textiles, y Marianne Gödel (nacida Handschuh), una mujer educada y culta quien permaneció cercana a Gödel durante toda su vida, (tal como puede observarse en la extensa correspondencia entre ambos). En el momento de su nacimiento su ciudad contaba con la mayoría de población de habla alemana[3] y este era el idioma de sus padres.
Gödel que hablaba muy poco el checo se convirtió automáticamente en checoslovaco a la edad de 12 años tras la caída del Imperio austrohúngaro al final de la Primera Guerra Mundial. Posteriormente le contó a su biógrafo John W. Dawson que durante ese tiempo se sentía como un "exiliado austríaco en Checoslovaquia" ("ein Österreicher im Exil in der Tschechoslowakei"). Decidió convertirse en ciudadano austríaco a la edad de 23 años. Cuando la Alemania nazi anexionó Austria Gödel automáticamente se convirtió en ciudadano alemán a la edad de 32 años. Después de la Segunda Guerra Mundial, a la edad de 42 años, se convirtió en ciudadano estadounidense.
En su familia, al joven Kurt lo llamaban Herr Warum (Sr. Por qué) debido a su insaciable curiosidad. La única excepción a una infancia sin incidentes fue el que a partir de los cuatro años Kurt sufrió quebrantos de salud y fiebres reumáticas, de las cuales se recuperó completamente, pero quedó convencido para el resto de su vida de que su corazón había sufrido un daño permanente.
Asistió a la escuela primaria y secundaria en idioma alemán en Brno de la cual se graduó con honores en 1923 y sobresalió en matemáticas, idiomas y religión. En el transcurso de su adolescencia Kurt estudió, entre otras materias, la Teoría de los colores de Goethe, críticas de Isaac Newton y la obra de Immanuel Kant.
Estudios en Viena[editar]
A la edad de 18 años Kurt se reunió con su hermano mayor Rudolf (nacido en 1902) e ingresó en la Universidad de Viena. Para entonces ya dominaba las matemáticas a nivel universitario y aunque en un principio pretendió estudiar física teórica, también asistió a cursos de filosofía impartidos por Heinrich Gomperz y de matemáticas. Durante este período adoptó ideas del empirismo matemático, leyó los Metaphysische Anfangsgründe der Naturwissenschaft (Fundamentos metafísicos de la ciencia natural) de Kant, y aunque él mismo no fue un positivista lógico participó en reuniones del Círculo de Viena con Moritz Schlick, Hans Hahn y Rudolf Carnap, siendo estos dos últimos de quienes aprendió lógica. Después estudió también la teoría de los números, y fue el asistir a un seminario dirigido por Schlick, en el cual se estudiaba el libro Introducción a la lógica matemática de Bertrand Russell, lo que lo motivó a interesarse por la lógica matemática.
El asistir a una conferencia de Hilbert sobre la completud y la consistencia de los sistemas matemáticos podría haber sido lo que decidió el curso de su vida. En 1928 Hilbert y Wilhelm Ackermann publicaron los Grundzüge der theoretischen Logik (Principios de lógica teórica), una introducción a la lógica de primer orden en la cual se planteaba el problema de la completud: “¿Son suficientes los axiomas de un sistema formal para derivar cada una de las proposiciones verdaderas en todos los modelos del sistema?” Este fue el tema elegido por Gödel para su disertación doctoral. En 1929, a la edad de 23 años, completó su disertación bajo la supervisión de Hans Hahn, en la cual Gödel estableció la completud del cálculo de predicados de primer orden (este resultado se conoce ahora como el teorema de completitud de Gödel). El doctorado le fue concedido en 1930 y su tesis, junto a trabajo adicional, fue publicada por la Academia de Ciencias de Viena.[5]
Obra en Viena[editar]
En 1931 Gödel publicó sus célebres teoremas de la incompletud en Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme (Sobre proposiciones formalmente indecidibles de Principia Mathematica y sistemas relacionados). En dicho artículo demostró que para todo sistema axiomático computable que sea lo suficientemente poderoso como para describir la aritmética de los números naturales (e.g. los axiomas de Peano (o ZFC), entonces:
- Si el sistema es coherente no puede ser completo. (A esto generalmente se le conoce como el teorema de la incompletud).
- La consistencia de los axiomas no puede demostrarse en el interior del sistema.
Estos teoremas finalizaron medio siglo de intentos académicos (comenzando con el trabajo de Frege y culminando en los Principia Mathematica y en el formalismo de Hilbert) por encontrar un conjunto de axiomas suficiente para toda la matemática. El teorema de la incompletud implica también que no toda la matemática es computable.
La idea básica del teorema de la incompletud es más bien simple. Esencialmente Gödel construyó una fórmula que asegura ser no-demostrable para cierto sistema formal. Si fuera demostrable sería falsa, lo cual contradice el hecho de que en un sistema consistente las proposiciones demostrables son siempre verdaderas. De modo que siempre habrá por lo menos una proposición verdadera pero no demostrable. Esto es, para todo conjunto de axiomas de la aritmética construible por el hombre existe una fórmula la cual se obtiene de la aritmética pero es indemostrable en ese sistema. Sin embargo, para precisar esto Gödel necesitaba resolver varias cuestiones técnicas, tales como proposiciones de codificación y el concepto mismo de demostrabilidad en la teoría de los números naturales. Esto último lo realizó mediante un proceso denominado numeración de Gödel.
En su ensayo de dos páginas Zum intuitionistischen Aussagenkalkül (1932) Gödel refutó la “valuabilidad” finita de la lógica intuicionista. En la demostración empleó implícitamente lo que después se conoció como la lógica intermedia de Gödel–Dummett (o Gödel fuzzy logic).
Gödel recibió su habilitación en la Universidad de Viena en 1932, y en 1933 se convirtió en Privatdozent (profesor no remunerado). La ascensión de Hitler en Alemania en 1933 afectó poco a Gödel en Viena, ya que tenía poco interés en la política. Sin embargo, se vio muy afectado por el asesinato de Moritz Schlick (cuyo seminario había despertado su interés por la lógica) a manos de un estudiante perturbado, incidente que resultó en su primer colapso nervioso.
Visitas a los Estados Unidos[editar]
En 1933 Gödel viajó por primera vez a los Estados Unidos donde conoció a Albert Einstein, con quien estrechó lazos de amistad. Presentó una conferencia en la reunión anual de la Sociedad Americana de Matemáticas. En el transcurso de ese año Gödel también desarrolló ideas sobre la computabilidad y la función recursiva al punto que presentó una conferencia sobre dichas funciones y sobre el concepto de verdad. Posteriormente, este trabajo se desarrolló en la teoría de los números, empleando la numeración de Gödel.
En 1934 Gödel presentó una serie de conferencias en el Instituto de Estudios Avanzados (IEA) en Princeton, titulada Sobre las proposiciones indecidibles de los sistemas matemáticos formales. Stephen Kleene, quien acababa de finalizar su doctorado en Princeton, tomó notas de esta conferencia, las cuales fueron publicadas posteriormente.
Gödel visitaría el IEA nuevamente en el otoño de 1935, pero los viajes y el intenso trabajo lo habían extenuado y al año siguiente convaleció producto de una depresión, y no regresó a la docencia sino hasta 1937. Durante ese tiempo se dedicó a la prueba de consistencia del axioma de elección y a la hipótesis del continuo en cuyo trabajo continuó hasta mostrar que estas hipótesis no pueden refutarse desde el sistema común de axiomas de la teoría de conjuntos.
Contrajo matrimonio el 20 de septiembre de 1938 con Adele Nimbursky (nacida Porkert, 1899-1981), a la cual conocía desde hacía 10 años. Los padres de Gödel se oponían a la relación sobre la base de que se trataba de una bailarina divorciada y seis años mayor que él. Nunca tuvieron hijos.
Posteriormente realizó otra visita a los Estados Unidos, donde pasó el otoño de 1938 en el IEA y la primavera de 1939 en la Universidad de Notre Dame. Durante sus vacaciones del IEA, Gödel y su esposa Adele pasaron el verano de 1942 en Blue Hill, Maine. Sin embargo Gödel no estaba meramente vacacionando pues tuvo un verano de trabajo muy productivo. John W. Dawson, Jr. conjetura que durante esas vacaciones Gödel, empleando el volumen 15 de su obra todavía sin publicar Arbeitshefte (Cuadernos de notas), descubrió una prueba de la independencia del axioma de elección de la teoría finita de tipos, una forma debilitada de la teoría de conjuntos. Hao Wang, amigo cercano de Gödel, apoya dicha conjetura, señalando que los cuadernos de notas de Blue Hill contienen su tratamiento más extenso del problema.
http://es.wikipedia.org/wiki/Kurt_G%C3%B6del
|
|
|
|
|
| m: Cajeli |
Sent: 09/01/2015 22:21 |
|
Stephen Hawking en su obra Historia del Tiempo, dice:
Se han encontrado nuevos y más razonables espacio-tiempos compatibles con la relatividad general y que permiten viajar al pasado. Uno de ellos es el interior de un agujero negro en rotación.
Otro es un espacio-tiempo que contiene dos cuerdas cósmicas en movimiento que se cruzan a alta velocidad. Como sugiere su nombre, las cuerdas cósmicas son objetos similares a cuerdas en el sentido de que su sección es mucho menor que su longitud. De hecho, son más bien como tiras de goma porque están sometidas a tensiones enormes, del orden de millones de millones de millones de millones de toneladas.
UNA CUERDA CÓSMICA UNIDA A LA TIERRA podría acelerarla de 0 a 100 km/h en la treintava parte de un segundo). Las cuerdas cósmicas pueden parecer pura ciencia ficción, pero hay razones para creer que se podrían haber formado en los primeros instantes del universo como resultado de una rotura de simetría similar a las discutidas en el capitulo 5. Debido a que estaría bajo tensiones enormes y podían empezar en una configuración cualquiera, serían capaces de acelerarse hasta velocidades altísimas al enderezarse.
La solución de Gödel y el espacio-tiempo de las cuerdas cósmicas comienzan tan distorsionados que el viaje al pasado es siempre posible. Dios [lo está diciendo Hawkig]podría haber creado un universo así de curvado, pero no poseemos razones para pensar que lo hiciera. Las observaciones del fondo de microondas y de la gran cantidad de elementos ligeros indican que el universo primitivo no poseía el tipo de curvatura necesario para permitir los viajes en el tiempo. A la misma conclusión se llega teóricamente a partir de la propuesta de no existencia de fronteras.
Así, la pregunta es: si el universo empieza sin la clase de curvatura requerida para viajar en el tiempo, ¿podemos posteriormente curvar regiones concretas del espacio-tiempo lo suficiente como para permitirlo?
…………..
Ahora la pregunta para el foro es:
Este agnosticismo de Hawking, y del mismo Carl Sagan quien escribió el prólogo de este libro, ¿contradice o ratifica lo que dice la Biblia acerca del universo y de las profecías? Claramente no. Si por lo menos existe la base teórica para ver el pasado, también el futuro completo está en la visión de Dios.
|
|
|
| From: Cajeli |
Sent: 09/01/2015 23:41 |
|
Los seguidores de la ciencia ficción suelen atribuir a H. G. Wells el concepto d elos viajes en el tiempo, por su famosa obra "La Maquina del Tiempo". Sin embargo es en la Biblia donde están los primeros viajes en el tiempo.
Josué 10.12 Entonces Josué habló a Jehová el día en que Jehová entregó al amorreo delante de los hijos de Israel, y dijo en presencia de los israelitas: Sol, detente en Gabaón; Y tú, luna, en el valle de Ajalón. 13 Y el sol se detuvo y la luna se paró, Hasta que la gente se hubo vengado de sus enemigos. ¿No está escrito esto en el libro de Jaser? Y el sol se paró en medio del cielo, y no se apresuró a ponerse casi un día entero.
2Reyes 20.8-11 Y Ezequías había dicho a Isaías: ¿Qué señal tendré de que Jehová me sanará, y que subiré a la casa de Jehová al tercer día? 9 Respondió Isaías: Esta señal tendrás de Jehová, de que hará Jehová esto que ha dicho: ¿Avanzará la sombra diez grados, o retrocederá diez grados? 10 Y Ezequías respondió: Fácil cosa es que la sombra decline diez grados; pero no que la sombra vuelva atrás diez grados. 11 Entonces el profeta Isaías clamó a Jehová; e hizo volver la sombra por los grados que había descendido en el reloj de Acaz, diez grados atrás.
|
|
|
|
1. Génesis 8:4: Y reposó el arca en el mes séptimo, a los diecisiete días del mes, sobre los montes de ARARAT.
2. 2 Reyes 19:37: Y aconteció que mientras él adoraba en el templo de Nisroc su dios, Adramelec y Sarezer sus hijos lo hirieron a espada, y huyeron a tierra de ARARAT. Y reinó en su lugar Esarhadón su hijo.
3. Isaías 37:38: Y aconteció que mientras adoraba en el templo de Nisroc su dios, sus hijos Adramelec y Sarezer le mataron a espada, y huyeron a la tierra de ARARAT; y reinó en su lugar Esarhadón su hijo.
4. Jeremías 51:27: Alzad bandera en la tierra, tocad trompeta en las naciones, preparad pueblos contra ella; juntad contra ella los reinos de ARARAT, de Mini y de Askenaz; señalad contra ella capitán, haced subir caballos como langostas erizadas.
|
|
|
|
LA "MAQUINA DEL TIEMPO", EN EL CONTEXTO A 2 DE REYES 20:8-11, ESTA EN EL MARCO AL "MONTE DE ARARAT". ESTO CONFIRMA EL NEXO DE GENESIS 8:4 CON LA "MAQUINA DEL TIEMPO"
1. Génesis 8:4: Y reposó el arca en el mes séptimo, a los diecisiete días del mes, sobre los montes de ARARAT.
2. 2 Reyes 19:37: Y aconteció que mientras él adoraba en el templo de Nisroc su dios, Adramelec y Sarezer sus hijos lo hirieron a espada, y huyeron a tierra de ARARAT. Y reinó en su lugar Esarhadón su hijo.
3. Isaías 37:38: Y aconteció que mientras adoraba en el templo de Nisroc su dios, sus hijos Adramelec y Sarezer le mataron a espada, y huyeron a la tierra de ARARAT; y reinó en su lugar Esarhadón su hijo.
4. Jeremías 51:27: Alzad bandera en la tierra, tocad trompeta en las naciones, preparad pueblos contra ella; juntad contra ella los reinos de ARARAT, de Mini y de Askenaz; señalad contra ella capitán, haced subir caballos como langostas erizadas.
INCLUSO ISAIAS 38 TAMBIEN ESTA RELACIONADO EN ESE CONTEXTO.
Isaías 38
1. En aquellos días Ezequías enfermó de muerte. Y vino a él el profeta Isaías hijo de Amoz, y le dijo: Jehová dice así: Ordena tu casa, porque morirás, y no vivirás.
2. Entonces volvió Ezequías su rostro a la pared, e hizo oración a Jehová,
3. y dijo: Oh Jehová, te ruego que te acuerdes ahora que he andado delante de ti en verdad y con íntegro corazón, y que he hecho lo que ha sido agradable delante de tus ojos. Y lloró Ezequías con gran lloro.
4. Entonces vino palabra de Jehová a Isaías, diciendo:
5. Ve y di a Ezequías: Jehová Dios de David tu padre dice así: He oído tu oración, y visto tus lágrimas; he aquí que yo añado a tus días quince años. (EL TODOPODEROSO ES LA "MAQUINA DEL TIEMPO". LOS EGOLATRAS QUE NO ENTIENDEN EL AMOR DE DIOS, NO PUEDEN RACIONALIZAR UN DIOS QUE MANEJE LA CIENCIA)
6. Y te libraré a ti y a esta ciudad, de mano del rey de Asiria; y a esta ciudad ampararé.
7. Y esto te será señal de parte de Jehová, que Jehová hará esto que ha dicho:
8. He aquí yo haré volver la sombra por los grados que ha descendido con el sol, en el reloj de Acaz, diez grados atrás. Y volvió el sol diez grados atrás, por los cuales había ya descendido. (HAY UN CLARO REGRESO EN EL TIEMPO. OBSERVAMOS QUE EN EL CONTEXTO A ISAIAS 37:38, TIENE NEXO CON EL "MONTE DE ARARAT". ESTE ES UN OBVIO NEXO CON EL CESAR, COMO LO HE HEMOS DEMOSTRADO POR LA GRACIA DE DIOS EN OTROS PANELES. EL NEXO DEL MONTE DE LA TRANSFIGURACION EN EL CONTEXTO A CESAREA (C-SAR =MONTE DE ARARAT = "EXPERIMENTO FILADELFIA") DE FILIPO, ESTA CONECTADO CON LA "MAQUINA DEL TIEMPO.)
9. Escritura de Ezequías rey de Judá, de cuando enfermó y sanó de su enfermedad:
10. Yo dije: A la mitad de mis días iré a las puertas del Seol; privado soy del resto de mis años.
11. Dije: No veré a JAH, a JAH en la tierra de los vivientes; ya no veré más hombre con los moradores del mundo.
|
|
|
|
|
|
 Primeira
Primeira
 Anterior
2 a 9 de 9
Seguinte
Anterior
2 a 9 de 9
Seguinte
 Última
Última

|

